Содержание статьи:
- Треугольная пирамида или тетраэдр
- Правильная пирамида с треугольным основанием и ее развертка
- Формула площади
- Решение задачи
Пирамида является совершенной геометрической фигурой, форму которой можно встретить в некоторых предметах из нашей жизни, например, в магических амулетах. В данной статье рассмотрим, как найти площадь правильной треугольной пирамиды и приведем соответствующую формулу.
Треугольная пирамида или тетраэдр
В геометрии пирамидой называют такой геометрический объект, который состоит из n треугольников и одного n-угольника. Все треугольники пересекаются в точке, которая называется вершиной фигуры, а n-угольник является ее основанием. Не сложно догадаться, что название пирамиды определяется числом сторон n-угольника.
 Вам будет интересно:«Подчинение» — это про выстраивание порядка
Вам будет интересно:«Подчинение» — это про выстраивание порядка
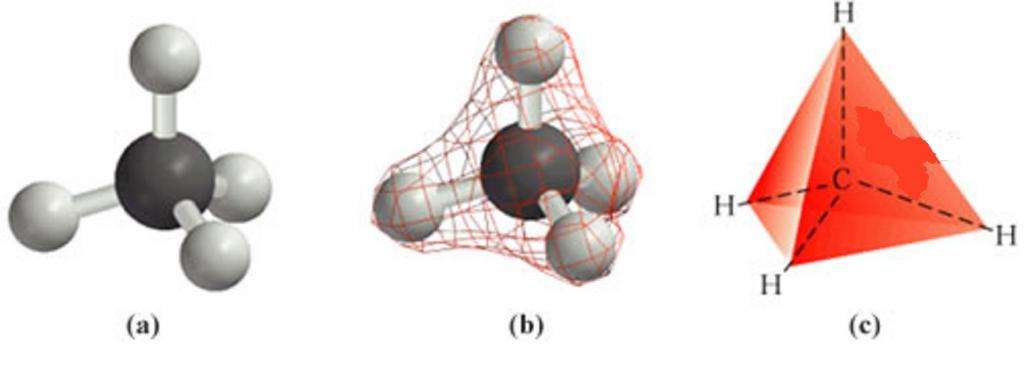
В соответствии с темой данной статьи, мы рассмотрим треугольную пирамиду. Ее n-угольным основанием является также треугольник. Поэтому такая пирамида состоит из 4 треугольных граней, каждую из которых можно рассматривать в качестве основания. У треугольной пирамиды 4 равноправных вершины и 6 ребер. Поскольку число сторон фигуры равно 4, то ее также называют тетраэдром. Для наглядности приведем изображение треугольной пирамиды:

На рисунке показан вид сверху на фигуру.
Правильная пирамида с треугольным основанием и ее развертка
В общем случае треугольником в основании может быть фигура произвольной формы. Однако если этим треугольником является равносторонняя фигура, и перпендикуляр, опущенный из вершины на основание, пересекает треугольник в его центре, тогда речь ведут о правильной пирамиде.
Правильная треугольная пирамида состоит из равностороннего треугольника, сторону которого обозначим буквой a, и трех равнобедренных треугольников, которые друг другу равны. При определенном соотношении высоты фигуры h и длины a равнобедренные треугольники могут стать равносторонними, тогда все четыре грани пирамиды будут равны между собой.
Для определения площади рассматриваемой фигуры проще всего выполнить ее развертку на плоскость. Рисунок ниже показывает, что представляет собой эта развертка.
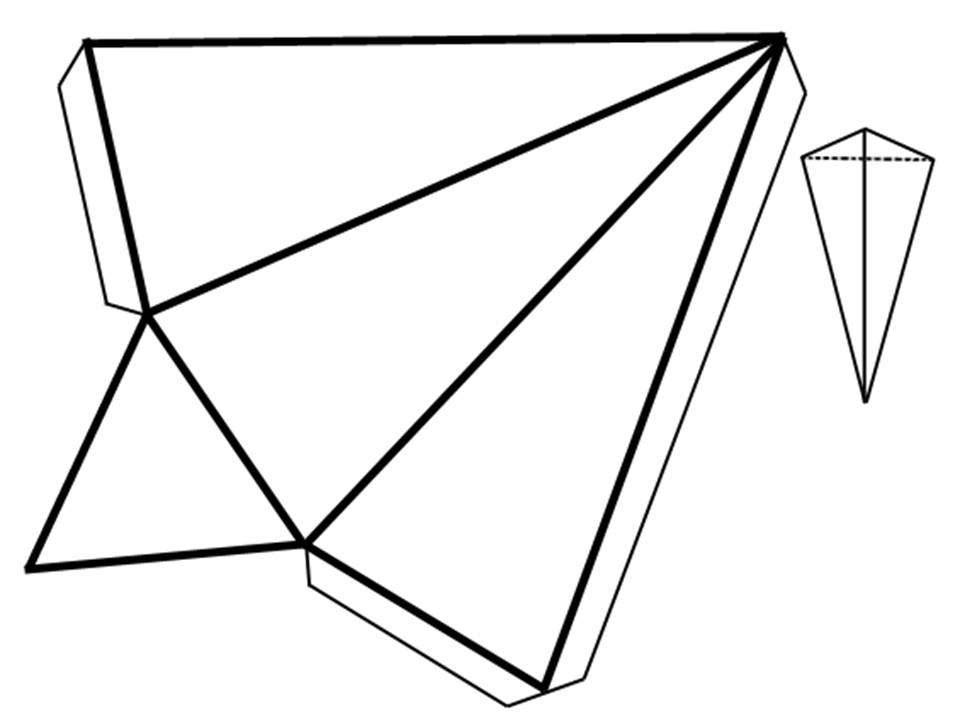
Здесь показаны четыре треугольника, из которых равносторонний является основанием пирамиды, а три равнобедренных фигуры составляют ее боковую поверхность. Сумма площадей всех треугольников образует площадь правильной треугольной пирамиды.
Формула площади
Из курса планиметрии каждый школьник знает, как найти площадь треугольника. Для этого следует произвести такие вычисления:
S3 = 1/2 * a * ha.
Здесь a – основание треугольника, ha – его высота (индекс a введен, чтобы отличать эту величину от высоты пирамиды h).
В случае равностороннего треугольника его высота равна:
ha = √3/2 * a.
Тогда формула основания площади правильной треугольной пирамиды приобретает вид:
S3 = 1/2 * a * √3/2 * a = √3/4 * a2.
То есть для определения площади основания достаточно знать только длину его стороны.
Чтобы определить площадь боковой поверхности Sb, введем понятие апофемы пирамиды. Апофемой называют высоту любого из боковых треугольников, которая опущена из вершины пирамиды на сторону основания. Все апофемы в правильной пирамиде равны друг другу. Обозначим их длины символом hb. Поскольку рассматриваемая пирамида состоит из трех боковых сторон, то площадь Sb вычисляется по формуле:
Sb = 3/2 * a * hb.
Остается сделать последний шаг, чтобы записать формулу площади правильной треугольной пирамиды:
S = S3 + Sb = √3/4 * a2 + 3/2 * a * hb.
Заметим, что площадь поверхности рассматриваемой геометрической фигуры определяется однозначно, если знать два линейных ее параметра (a и hb).
Решение задачи
Высота основания правильной треугольной пирамиды равна 10 см. Высота же самой фигуры в два раза больше длины стороны основания. Чему равна площадь поверхности этой пирамиды?

Поскольку нам известно значение высоты основания и отношение между высотой фигуры с стороной равностороннего треугольника, то этой информации достаточно, чтобы ответить на вопрос задачи. В первую очередь определим сторону a и значение высота h, имеем:
ha = √3/2 * a;
a = 2 * ha / √3 = 11,547 см;
h = 2 * a = 23,094 см.
В параграфе выше была приведена формула для S, однако ей воспользоваться на данном этапе задачи мы не можем, поскольку мы не знаем апофему hb. Последнюю несложно вычислить, если увидеть, что она является гипотенузой в прямоугольном треугольнике, катетами которого будут высота h и 1/3 высоты основания. Учитывая сказанное, получаем:
hb = √(h2 + (1/3 * ha)2) = √(23,0942 + (1/3 * 10)2) = 23,333 см.
Заметим, что значение hb немного больше, чем высота h фигуры.
Мы нашли все параметры, которые стоят в формуле для S, теперь можно вычислить искомую площадь:
S = √3/4 * a2 + 3/2 * a * hb = √3/4 * 11,5472 + 3/2 * 11,547 * 23,333 = 409,14 см2.
Формула для S записана в таком виде, что позволяет отдельно определить площадь основания и боковой поверхности.
Изучая объемные фигуры в курсе стереометрии, школьники часто сталкиваются с задачей определения площади их поверхности. Успешное решение этой задачи возможно, если четко представлять, с какой фигурой ведется работа. Данная статья посвящена вопросу определения площади поверхности правильной пирамиды (четырехугольной).
Описание фигуры
Начнем раскрытие вопроса статьи с определения правильной четырехугольной пирамиды. Под ней в геометрии понимают фигуру в пространстве, которая образована одним квадратом и четырьмя одинаковыми равнобедренными треугольниками (при определенных параметрах фигуры эти треугольники могут быть равносторонними). Пример рассматриваемой фигуры показан ниже.
 Вам будет интересно:Егерские полки – прообраз современного спецназа
Вам будет интересно:Егерские полки – прообраз современного спецназа

Каждый равнобедренный треугольник пересекается по боковым граням с двумя соседними треугольниками, и по грани основания – с квадратом. Кроме того, все четыре треугольника пересекаются в одной точке, которая носит название главной вершины пирамиды. Помимо нее, фигура имеет еще четыре вершины, но все они принадлежат основанию.
Четырехугольной эта пирамида называется потому, что ее основание является четырехугольником. А правильной она считается потому, что это основание представляет собой квадрат, и сама фигура является прямой. Последнее означает, что опущенный с вершины перпендикуляр на квадрат пересекает его точно в геометрическом центре.
Что собой представляет площадь поверхности правильной пирамиды (четырехугольной)
Многим будет нелегко ответить на этот вопрос. Действительно, мы рассматриваем объемную фигуру, а когда говорят о площадях, то имеют в виду силуэт на плоскости. В связи со сказанным в геометрии для вычисления площадей пространственных объектов используют их плоские развертки.

Развертку рассматриваемой пирамиды получить несложно. Предположим, что у нас имеется бумажная фигура с квадратным основанием. Возьмем ножницы и отрежем от нее квадрат. Затем разрежем вдоль бокового ребра (отрезок пересечения треугольников) пирамидальную поверхность и развернем ее в плоскую интерпретацию. В результате этих действий у нас получится плоская фигура, подобная той, что показана на рисунке.
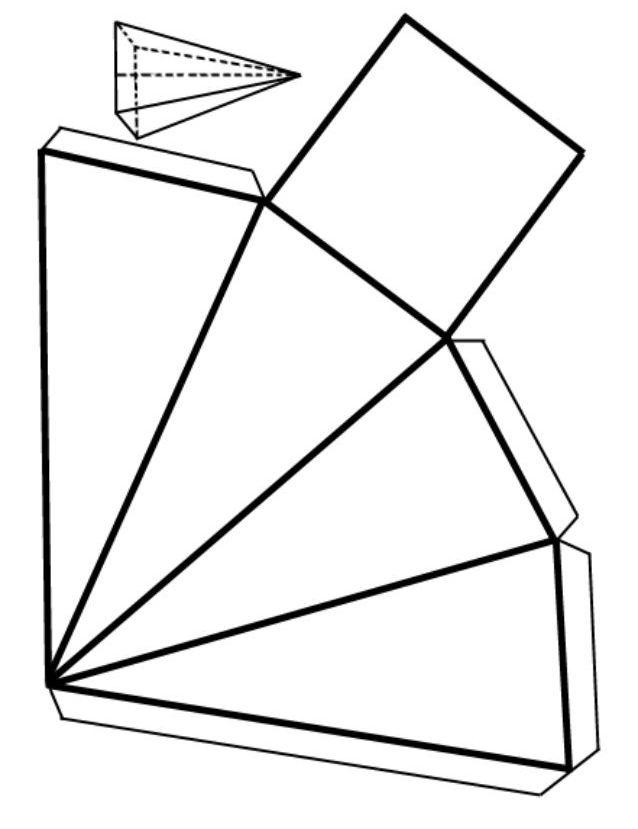
Таким образом, отвечая на вопрос, как найти площадь правильной четырехугольной пирамиды, следует сказать, что для этого нужно сложить площадь квадрата и площади четырех одинаковых треугольников.
Формулы для нахождения величины
Из планиметрии известно, что расчет площади производится с учетом знания линейных параметров плоской фигуры. В нашем случае речь идет о двух типах объектов: равнобедренном треугольнике и квадрате.
Обозначим сторону четырехугольника буквой a, а высоту треугольника hb (она называется апофемой пирамиды). Тогда для площади So квадрата можно записать:
So = a2
Площадь же треугольника S3 будет равна:
S3 = 1 / 2 * a * hb
Поскольку треугольников с площадью S3 в рассматриваемой пирамиде четыре штуки, то формула площади поверхности правильной пирамиды (четырехугольной) примет вид:
S = So + 4 * S3 = a2 + 4 / 2 * a * hb = a * (a + 2 * hb)
При решении некоторых задач вместо апофемы hb может быть известен другой линейный параметр пирамиды – высота h. Поэтому будет полезным, если мы здесь приведем формулу для S через параметры a и h.
Решить поставленную задачу можно, если увидеть внутри пирамиды треугольник прямоугольный, и рассчитать гипотенузу-апофему по следующей формуле:
hb = √(h2 + a2 / 4)
Подставляя это выражение в записанную выше формулу для S, получаем:
S = a * (a + 2 * √(h2 + a2 / 4))
Это выражение выглядит несколько сложнее, чем первое. Тем не менее, оно чаще используется при рассмотрении геометрических проблем с четырехугольной пирамидой.
Записанные формулы для площади рассматриваемой фигуры можно не запоминать, важно лишь ясно представлять развертку пирамиды и уметь находить площадь треугольника.
Использование формулы площади четырехугольной пирамиды на примере сооружения Хеопса

Конечно же, речь идет о пирамиде Хеопса – самой знаменитой каменной постройки за всю известную нам историю. Рассчитаем площадь поверхности этого гиганта, используя следующие данные о нем:
- среднее значение длины стороны основания равно 230,363 метра;
- начальная высота сооружения составляла 146,50 метра.
Чтобы найти искомую площадь, следует воспользоваться второй формулой, приведенной в предыдущем пункте статьи. Сделаем это:
S = a * (a +2 * √(h2 + a2 / 4)) = 230,3632 + 230,363 * 2 * √(146,502 + 230,3632 / 4) ≈ 138 927 м2
Чтобы понять, насколько огромно рассчитанное значение, сравним его с параметрами футбольного поля (5 000 м2). Полная площадь поверхности правильной четырехугольной пирамиды Хеопса почти в 28 раз больше величины площадки для игры.
Автор:

21-12-2018 01:05
Жду ваши вопросы и мнения в комментариях
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.
Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.
-
Формула площади правильной пирамиды
- 1. Общая формула
- 2. Площадь правильной треугольной пирамиды
- 3. Площадь правильной четырехугольной пирамиды
- 4. Площадь правильной шестиугольной пирамиды
Формула площади правильной пирамиды

1. Общая формула
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.
Sполн. = Sбок. + Sосн.
Боковой гранью правильной пирамиды является равнобедренный треугольник.

Площадь треугольника вычисляется по формулам:
1. Через длину основания (a) и высоту (h):

2. Через основание (a) и боковую сторону (b):

Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
2. Площадь правильной треугольной пирамиды

Основание: равносторонний треугольник.
L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.
3. Площадь правильной четырехугольной пирамиды

Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 2aL |
 |
|
| полная | Sполн. = a2 + 2aL |
 |
microexcel.ru
4. Площадь правильной шестиугольной пирамиды

Основание: правильный шестиугольник
1.
Развертка, площадь боковой и
полной поверхности
пирамиды и усеченной
пирамиды.
2.
• Ты узнаешь:
• элементы пирамиды.
• Ты научишься:
• определять развертку пирамиды;
• находить площади боковой поверхности и полной поверхности
пирамиды.
3.
Развертка пирамиды представляет собой
фигуру, состоящую из многоугольника в
основании и стольких треугольников, сколько
сторон в основании.
4.
• Площадью полной поверхности пирамиды называется сумма
всех ее граней, то есть основания и боковых граней.
• S пп = S осн + S бп
• Обозначения:
• Sпп – площадь полной поверхности пирамиды;
• Sосн – площадь основания пирамиды;
• Sбп – площадь боковой поверхности пирамиды.
5.
• Теорема. Площадь боковой поверхности правильной пирамиды
равна половине произведения периметра основания на апофему.
• S бп =
1
⋅
2
P осн ⋅ l
• S бп – площадь боковой поверхности пирамиды
• P осн – периметр основания, l – апофема
6.
• Существуют еще формулы площади боковой поверхности правильной
пирамиды через площадь ортогональной проекции.
7.
Задача 1
• Стороны основания треугольной пирамиды равны 13 см, 14 см
и 15 см. Плоскости боковых граней наклонены к основанию под
углом 60°. Найди площадь полной поверхности пирамиды.
8.
Задача 2
9.
Задача 3
10.
Задача 4
• Представь, что ты работаешь на
предприятии, которое изготавливает
упаковки для молока в форме
тетраэдра, вместимостью 0,5 л. Надо
рассчитать количество материала для
изготовления 1 коробки. Грани коробки
представляют собой правильные
треугольники со стороной 12 см и
высотой 10 см. Определи площадь
поверхности упаковки, имеющей
форму правильного тетраэдра.
11.
Задача 5
Как найти площадь поверхности пирамиды
На данной странице калькулятор поможет рассчитать площадь поверхности пирамиды онлайн. Для расчета задайте площадь основания и апофему.
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.
Апофема – опущенный перпендикуляр из вершины на ребро основания.
Боковая поверхность через периметр и апофему
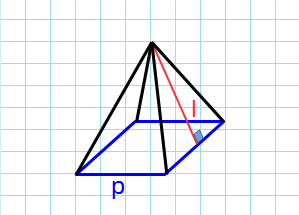
Формула площади боковой поверхности правильной пирамиды через периметр и апофему:
p – периметр основания пирамиды; l – апофема пирамиды.
Боковая поверхность через высоту и сторону основания
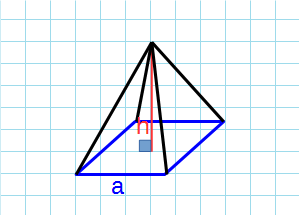
Формула площади боковой поверхности правильной пирамиды через высоту и сторону основания:
a – сторона основания; h – высота пирамиды; n – число сторон в основании.
Полная поверхность через высоту и сторону основания

Формула площади полной поверхности правильной пирамиды через высоту и сторону основания:
a – сторона основания; h – высота пирамиды; n – число сторон в основании.
Полная площадь тетраэдра
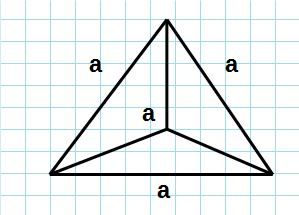
Формула полной площадь тетраэдра:
a – сторона основания.
