На этом уроке мы выведем и научимся применять
формулы для вычисления площади боковой поверхности конуса и площади полной
поверхности конуса.
Для начала давайте вспомним, что же это за
геометрическое тело – конус.
Итак, тело, ограниченное
конической поверхностью и кругом с границей , называется конусом.
Напомним, что боковой поверхностью конуса
называется фигура, образованная всеми образующими конуса.
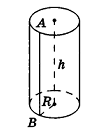
На экране изображён конус, у которого радиус
равен , а
образующая равна . Боковую
поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на
плоскость, разрезав её по одной из образующих.
Давайте представим, что боковую поверхность
конуса разрезали по образующей и развернули
таким образом, что получился круговой сектор .
Стороны и
которого
являются двумя краями разреза боковой поверхности конуса.
Развёрткой боковой поверхности
конуса является круговой сектор. Обратите внимание, радиус сектора равен
образующей конуса, т.е. .
А длина дуги сектора равна длине окружности основания конуса, т.е. равна .
За площадь боковой поверхности конуса
принимается площадь её развёртки. Выразим площадь боковой поверхности конуса
через его образующую и радиус
основания .
Площадь кругового сектора – развёртки боковой
поверхности конуса – равна , где
– градусная
мера дуги .
Выразим через длину
дуги и радиус окружности. Длина дуги окружности с градусной мерой и радиусом
равна
. С другой
стороны, длина этой дуги равна два пи эр, т.е. пи эль альфа деленное на сто
восемьдесят равно . Отсюда,
. Подставим
это выражение в формулу площади боковой поверхности конуса. Тогда площадь
боковой поверхности конуса равна . Т.е.
площадь боковой поверхности конуса с образующей и радиусом
основания выражается следующей
формулой: .
Таким образом, площадь боковой поверхности
конуса равна произведению половины длины окружности основания на образующую.
Теперь выведем формулу для вычисления площади
полной поверхности конуса.
Вообще, площадью полной поверхности
конуса называется сумма площадей боковой поверхности и основания. Формулу
для вычисления площади боковой поверхности конуса мы с вами выразили выше, а площадь круга равна
. Подставим
все данные в формулу.
Упростим. Отсюда, получаем, что площадь полной
поверхности конуса равна .
А сейчас давайте решим несколько задач на
применение выведенных формул.
Задача: образующая конуса равна
см, а его
высота – см.
Вычислите площадь боковой поверхности конуса.
Решение: запишем формулу для
вычисления площади боковой поверхности конуса.
Теперь внимательно рассмотрим рисунок.
Напомним, что высота конуса перпендикулярна
его основанию. А, значит, она перпендикулярна любой прямой, лежащей в плоскости
основания конуса. Следовательно, высота конуса .
Рассмотрим . Он
прямоугольный. Применяя теорему Пифагора, найдём длину стороны , которая и
является радиусом основания конуса. Получаем, что ОА равно
.
Подставим длину образующей конуса и его радиус
в формулу для вычисления площади боковой поверхности конуса. Посчитаем.
Получим, что площадь боковой поверхности конуса равна .
Запишем ответ.
Задача: радиус основания конуса
равен дм, а
площадь его осевого сечения – дм2.
Вычислите площадь боковой поверхности конуса.
Решение: запишем формулу для
вычисления площади боковой поверхности конуса.
Теперь рассмотрим рисунок.
Напомним, что осевым сечением конуса называется сечение
конуса плоскостью, проходящей через его ось, и представляет собой равнобедренный треугольник, основание которого –
диаметр основания конуса, а боковые стороны – образующие конуса. Значит, – равнобедренный.
Так как по
условию задачи радиус основания конуса равен 9 дм, то основание осевого сечения
равно
.
Напомним, что
площадь треугольника равна половине произведения длины основания на высоту . Выразим из формулы высоту
. Получаем, что высота треугольника, а она является и
высотой конуса, равна
.
Рассмотрим . Он прямоугольный, так как
. Применяя теорему Пифагора, найдём длину
. Получаем, что
. Обратите внимание, гипотенуза
есть образующая нашего конуса.
Подставим
найденную длину образующей конуса и его радиус в формулу для вычисления площади
боковой поверхности конуса. Посчитаем. Получим, что площадь боковой поверхности
конуса равна
.
Не забудем
записать ответ.
Задача: прямоугольный треугольник, длины катетов которого
равны см и
см, вращается вокруг меньшего катета. Вычислите
площадь полной поверхности конуса, образованного при этом вращении.
Решение: запишем формулу для вычисления площади полной
поверхности конуса.
Рассмотрим . Он прямоугольный по условию.
Воспользуемся теоремой
Пифагора и найдём длину гипотенузы , которая и является образующей конуса. Имеем,
.
Так как по
условию задачи треугольник вращается вокруг меньшего катета, то радиус
основания конуса, образованного при этом вращении, равен .
Подставим длину
образующей конуса и его радиус в формулу для вычисления площади полной
поверхности конуса. Посчитаем. Получим, что площадь полной поверхности нашего
конуса равна .
Запишем ответ.
Итоги:
На этом уроке
мы вывели формулы для вычисления площади боковой поверхности конуса и
площади полной поверхности конуса. А также научились их применять при решении
задач.
§ 18. Конус
18.1.Определение конуса и его элементов
Определение. Тело, которое образуется при вращении прямоугольного треугольника вокруг прямой, содержащей его катет, называется прямым круговым конусом (рис. 165, 166).
Отрезок оси вращения, заключённый внутри конуса, называется осью конуса.
Круг, образованный при вращении второго катета, называется основанием конуса. Длина этого катета называется радиусом основания конуса или, короче, радиусом конуса. Вершина острого угла вращающегося треугольника, лежащая на оси вращения, называется вершиной конуса. На рисунках 165, б и 166 вершиной конуса является точка Р.
Высотой конуса называется отрезок, проведённый из вершины конуса перпендикулярно его основанию. Длину этого перпендикуляра также называют высотой конуса. Высота конуса имеет своим основанием центр круга — основания конуса — и совпадает с осью конуса.
Отрезки, соединяющие вершину конуса с точками окружности его основания, называются образующими конуса. Все образующие конуса равны между собой (почему?).
Как и в случае с цилиндром, можно рассматривать конус в более широком, чем у нас, понимании, когда в основании конуса может быть, например, эллипс (эллиптический конус), парабола (параболический конус). Мы будем изучать только определённый выше прямой круговой конус (конус вращения), поэтому слова «прямой круговой» мы будем опускать.

Рис. 165

Рис. 166

Рис. 167
Поверхность, полученная при вращении гипотенузы, называется боковой поверхностью конуса, а её площадь — площадью боковой поверхности конуса и обозначается Sбок. Боковая поверхность конуса является объединением всех его образующих.
Объединение боковой поверхности конуса и его основания называется полной поверхностью конуса, а её площадь называется площадью полной поверхности конуса или, короче, площадью поверхности конуса и обозначается Sкон. Из этого определения следует, что
Sкон = Sбок + Sосн.
Если вокруг данной прямой — оси — вращать пересекающую её прямую, то при этом вращении образуется поверхность, которую называют круговой конической поверхностью или конической поверхностью вращения. Уравнение  +
+  –
–  = 0 задаёт коническую поверхность вращения с осью вращения Oz (рис. 167). Из этого уравнения следует, что коническая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» — в конце этой книги.)
= 0 задаёт коническую поверхность вращения с осью вращения Oz (рис. 167). Из этого уравнения следует, что коническая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» — в конце этой книги.)
18.2. Сечения конуса
Определение. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением конуса.

Рис. 168

Рис. 169

Рис. 170
Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники. На рисунке 168 осевым сечением конуса является треугольник ABP (АР = ВР). Угол АPВ называют углом при вершине осевого сечения конуса.
Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.
Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP).
Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).
Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением.

Рис. 171
 Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками.
Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками.
О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги. 
ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60°; б) в 90°. Найти площадь сечения.

Решение. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.
Хорда АВ окружности основания стягивает дугу в 60°, значит, △ AOB — правильный и АВ = R.
Рис. 172
Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S△ ABP =  АВ•РC. Имеем: ОР = R (по условию); в △ AOB: ОС =
АВ•РC. Имеем: ОР = R (по условию); в △ AOB: ОС =  ; в △ ОСР: CP =
; в △ ОСР: CP =  =
=  .
.
Тогда S△ ABP =  АВ•РС =
АВ•РС =  .
.
Ответ: а)  .
.
18.3. Касательная плоскость к конусу
Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.

Рис. 173
Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.

Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.
18.4. Изображение конуса

Рис. 174
Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).
Для достижения наглядности изображения невидимые линии изображают штрихами.
Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.
18.5. Развёртка и площадь поверхности конуса
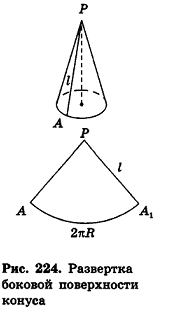
Пусть l — длина образующей, R — радиус основания конуса с вершиной Р.

Рис. 175

Рис. 176
Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a), то получим развёртку поверхности конуса (рис. 176, б), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):
α =  .
.
За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.
Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле
Sбок =  α•l2,(1)
α•l2,(1)
где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α =  , получаем:
, получаем:
Sбок = πRl.(2)
Таким образом, доказана следующая теорема.

Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼
Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.
Sкон = πRl + πR2.(3)

Следствие. Пусть конус образован вращением прямоугольного треугольника ABC вокруг катета АС (рис. 177). Тогда Sбок = π•BC•АВ. Если D — середина отрезка АВ, то AB = 2AD, поэтому
Sбок = 2 π ВС•AD.(4)

Рис. 177
Проведём DE ⟂ АB (E ∈ l = AС). Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А) имеем
 =
=  ⇒ BC•AD = DE•АС.(5)
⇒ BC•AD = DE•АС.(5)
Тогда соотношение (4) принимает вид
Sбок = (2π•DE)•AC,(6)
т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.
Это следствие будет использовано в п. 19.7.
18.6. Свойства параллельных сечений конуса


Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Рис. 178
Доказательство. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α, параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).
Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β, α || β, то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O1 = α ∩ РО. Обозначим этот круг F1.
Рассмотрим гомотетию  с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).
с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия  отображает основание F конуса на его параллельное сечение — круг F1, при этом центр О основания отображается на центр О1 круга F1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии
отображает основание F конуса на его параллельное сечение — круг F1, при этом центр О основания отображается на центр О1 круга F1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии  точка X отображается на точку X1 = РX ∩ α. Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:
точка X отображается на точку X1 = РX ∩ α. Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:
 =
=  = k,(*)
= k,(*)
где k — коэффициент гомотетии  , т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.
, т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.
А поскольку гомотетия является подобием, то круг F1, являющийся параллельным сечением конуса, подобен его основанию.
Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO1 : РО, где РO1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
Sсечен : Sоснов = k2 =  : PO2.
: PO2.
Теорема доказана. ▼
18.7.Вписанные в конус и описанные около конуса пирамиды
Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.
Для построения изображения правильной пирамиды, вписанной в конус:
—строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;
—соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;
—выделяют видимые и невидимые (штрихами) линии изображаемых фигур.
На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:
—прямоугольный треугольник (см. рис. 179);
—правильный треугольник (см. рис. 180);
—квадрат (см. рис. 181);
—правильный шестиугольник (см. рис. 182).

Рис. 179

Рис. 180

Рис. 181

Рис. 182
Определение. Пирамида называется описанной около конуса, если у них вершина общая, а основание пирамиды описано около основания конуса. В этом случае конус называют вписанным в пирамиду (рис. 183).

Рис. 183

Рис. 184
ЗАДАЧА (3.080). В равносторонний конус вписана правильная пирамида. Найти отношение площадей боковых поверхностей пирамиды и конуса, если пирамида: а) треугольная; б) четырёхугольная; в) шестиугольная.
Решение. Рассмотрим случай а). Пусть R — радиус основания равностороннего конуса, РАВС — правильная пирамида, вписанная в этот конус (рис. 184); △ DPE — осевое сечение конуса, CF — медиана △ АBС. Тогда в △ АВС (правильный): АВ = R , OF =
, OF =  R; в △ DPE (правильный): ОР =
R; в △ DPE (правильный): ОР =  = R
= R ; в △ ОРF (∠ FOP = 90°):
; в △ ОРF (∠ FOP = 90°):
PF =  =
=  .
.
Так как CF — медиана △ АВС, то PF — высота равнобедренного треугольника АВР. Поэтому
S△ ABP =  AB•PF =
AB•PF =  R
R •
•  =
=  .
.
Обозначим: S1 — площадь боковой поверхности пирамиды, S2 — площадь боковой поверхности конуса. Тогда
S1 = 3S△ ABP =  ,
,
S
2 = πR•PA = πR•2R = 2πR2.
Следовательно,
S1 : S2 =  : 2πR2 =
: 2πR2 =  .
.
Ответ: а)  .
.


 Во многих пособиях по геометрии за площадь боковой поверхности конуса принимают предел последовательности боковых поверхностей правильных вписанных в конус (или описанных около конуса) п-угольных пирамид при n → +∞. Действительно, Sбок. пов. пирам =
Во многих пособиях по геометрии за площадь боковой поверхности конуса принимают предел последовательности боковых поверхностей правильных вписанных в конус (или описанных около конуса) п-угольных пирамид при n → +∞. Действительно, Sбок. пов. пирам =  •a•Poсн. пирам, где Рoсн. пирам — периметр основания пирамиды, а — апофема боковой грани. Для правильных описанных около конуса пирамид апофема a — постоянная величина, равная образующей l конуса, а предел последовательности периметров правильных многоугольников, описанных около окружности радиуса R основания конуса, равен 2πR — длине этой окружности. Таким образом, мы вновь получаем: Sбок = πRl.
•a•Poсн. пирам, где Рoсн. пирам — периметр основания пирамиды, а — апофема боковой грани. Для правильных описанных около конуса пирамид апофема a — постоянная величина, равная образующей l конуса, а предел последовательности периметров правильных многоугольников, описанных около окружности радиуса R основания конуса, равен 2πR — длине этой окружности. Таким образом, мы вновь получаем: Sбок = πRl. 
18.8. Усечённый конус

Рис. 185
Пусть дан конус с вершиной Р. Проведём плоскость α, параллельную плоскости основания конуса и пересекающую этот конус (рис. 185). Эта плоскость пересекает данный конус по кругу и разбивает его на два тела: одно из них является конусом, а другое (расположенное между плоскостью основания данного конуса и секущей плоскостью) называют усечённым конусом. Таким образом, усечённый конус представляет собой часть полного конуса, заключённую между его основанием и параллельной ему плоскостью. Основание данного конуса и круг, полученный в сечении этого конуса плоскостью α, называются соответственно нижним и верхним основаниями усечённого конуса. Высотой усечённого конуса называется перпендикуляр, проведённый из какой-либо точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённого конуса. (Часто за высоту усечённого конуса принимают отрезок, соединяющий центры его оснований.)

Рис. 186

Рис. 187
Часть боковой поверхности данного конуса, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса, а отрезки образующих конуса, заключённые между основаниями усечённого конуса, называются образующими усечённого конуса. Так как все образующие данного конуса равны и равны все образующие отсечённого конуса, то равны все образующие усечённого конуса.
Построение изображения усечённого конуса следует начинать с изображения того конуса, из которого получился усечённый конус (рис. 186).
На рисунке 187 показана развёртка усечённого конуса.
Из теоремы 28 следует, что основания усечённого конуса — подобные круги.
Определения усечённой пирамиды, вписанной в усечённый конус и описанной около него, аналогичны определениям пирамиды, вписанной в конус и описанной около него.
Заметим, что построение изображений усечённой пирамиды, вписанной в усечённый конус и описанной около него, следует начинать с изображений того конуса или той пирамиды, из которых получены соответственно усечённые конус и пирамида.
Полной поверхностью усечённого конуса называется объединение боковой поверхности этого конуса и двух его оснований. Иногда полную поверхность усечённого конуса называют его поверхностью, а её площадь — площадью поверхности усечённого конуса. Эта площадь равна сумме площадей боковой поверхности и оснований усечённого конуса.
Усечённый конус может быть образован также вращением прямоугольной трапеции вокруг боковой стороны трапеции, перпендикулярной её основанию.

Рис. 188
На рисунке 188 изображён усечённый конус, образованный вращением прямоугольной трапеции ABCD вокруг стороны CD. При этом боковая поверхность усечённого конуса образована вращением боковой стороны АВ, а основания его — вращением оснований AD и ВС трапеции.
18.9. Поверхность усечённого конуса
Выразим площадь Sбок боковой поверхности усечённого конуса через длину l его образующей и радиусы R и r оснований (R > r).

Рис. 189
Пусть точка Р — вершина конуса, из которого получен усечённый конус; точки О, O1 — центры оснований усечённого конуса; AA1 = l — одна из образующих усечённого конуса (рис. 189).
Используя формулу (2) п. 18.5, получаем
Sбок = πR•PA – πr•РA1 =
= πR(РA1 + А1A) – πr•PA1 =
= πR•A1A + π(R – r)•PA1.
Учитывая, что A1A = l, имеем
Sбок = πRl + π(R – r)PA1.(7)
Выразим PA1 через l, R и r. Так как O1A1 || OA и OO1 — высота усечённого конуса, то прямоугольные треугольники POA и PO1A1 подобны. Поэтому АО : А1O1 = PA : PA1 или
R : r = (PA1 + A1A) : PA1, откуда
R•PA1 = r(PA1 + l) ⇒ (R – r)PA1 = rl ⇒ PA1 =  .
.
Подставив это значение РА1 в (7), получаем
Sбок = π(R + r)l.(8)
Таким образом, доказана следующая теорема.

Теорема 29. Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую. ▼
Площадь полной поверхности усечённого конуса находится по формуле:
Sполн = π•(R + r)•l + π•R2 + π•r2.

Следствие. Пусть усечённый конус образован вращением прямоугольной трапеции ABCD вокруг её высоты AD (рис. 190). Тогда Sбок = π (АВ + DC)•ВС. Если KЕ — средняя линия трапеции, то АВ + DC = 2KE, поэтому
Sбок = 2π•KE•BC.(9)

Рис. 190
Проведём EF ⟂ ВС. Из подобия прямоугольных треугольников ВСН и EFK имеем
BC : EF = BH : KE ⇒ ⇒ KE•BC = EF•BH.(10)
Тогда равенство (9) принимает вид
Sбок = (2π•EF)•ВH,(11)

т. е. боковая поверхность усечённого конуса равна произведению его высоты на длину окружности, радиус которой равен серединному перпендикуляру, проведённому из точки оси конуса к его образующей.
18.10. Объёмы конуса и усечённого конуса
Найдём объём конуса, высота которого равна h и радиус основания — R. Для этого расположим этот конус и правильную четырёхугольную пирамиду, высота которой равна h и сторона основания — R, так, чтобы их основания находились на одной и той же плоскости α, а вершины — также в одной и той же плоскости β, параллельной плоскости α и удалённой от неё на расстояние h (рис. 191).

Рис. 191
Каждая плоскость, параллельная данным плоскостям и пересекающая конус, пересекает также пирамиду; причём площади сечений, образованных при пересечении обоих тел, относятся к площадям оснований этих тел, как квадраты их расстояний от вершин. А так как секущие плоскости для пирамиды и для конуса равноудалены от их вершин, то  =
=  . Тогда
. Тогда  =
=  =
=  = π, значит, для объёмов этих тел выполняется:
= π, значит, для объёмов этих тел выполняется:
Vкон : Vпир = π : 1 или Vкон :  R2•h = π : 1, откуда
R2•h = π : 1, откуда
Vкон =  πR2 •h.
πR2 •h.

Рис. 192
Самостоятельно рассмотрите усечённые конус и пирамиду, расположенные в соответствии с условиями принципа Кавальери. Тогда вы получите формулу вычисления объёма усечённого конуса:
Vус. кон =  π•h•(R2 + r•R + r2).
π•h•(R2 + r•R + r2).
Эту же формулу вы можете вывести, если используете идею подобия так же, как это сделано в случае с выводом формулы площади боковой поверхности усечённого конуса.

Используя принцип Кавальери, докажите, что объём каждого из тел, на которые конус разбивается его сечением плоскостью, проходящей через вершину (рис. 192), может быть вычислен по формуле V =  •h•Scегм, где h — длина высоты конуса, а Sceгм — площадь соответствующего сегмента основания конуса.
•h•Scегм, где h — длина высоты конуса, а Sceгм — площадь соответствующего сегмента основания конуса.
Площадь поверхности конуса состоит из площади боковой поверхности конуса и площади основания (круга).
|
Рис. (1). Конус |
Площадь боковой поверхности конуса вычисляется по формуле: где (R) — радиус конуса, (l) — образующая конуса. Площадь основания конуса вычисляется по формуле S(круга) = Площадь полной поверхности конуса вычисляется по формуле S(полн.) =S(бок.) +S(круга) =πRl+πR2. Объём конуса вычисляют по формуле V = 13⋅H⋅ S(круга) = πR2⋅H3 |
Площадью боковой поверхности конуса является площадь её развёртки.
Развёрткой боковой поверхности конуса является круговой сектор.
|
Рис. (2). Развёртка конуса |
α
— градусная мера центрального угла. Радиус этого сектора — образующая конуса (AK = KB = l)
|
Источники:
Рис. 1. Конус. © Якласс
Рис. 2. Развёртка конуса. © Якласс
Каждая объемная фигура, которая имеет конечные линейные размеры, обладает в пространстве некоторой площадью поверхности. В статье рассмотрим, чему равна площадь боковой поверхности конуса, приведем соответствующие формулы и покажем, откуда они выводятся.
Что такое конус?
В общем случае конусом в геометрии называют любую пространственную фигуру, которая образована в результате соединения фиксированной точки пространства со всеми точками некоторой плоской кривой. Фиксированная точка называется вершиной фигуры. Отрезки, соединяющие ее с кривой, получили название генератрис, или образующих, поскольку их совокупность образует коническую поверхность. Кривая, на которую опирается эта поверхность, называется директрисой, то есть направляющей. Директрисой может быть произвольная кривая, например, гипербола, окружность, парабола, эллипс и так далее. Образованный на них конус будет гиперболическим, круглым, параболическим и эллиптическим, соответственно.

Выше рисунок демонстрирует пример двух одинаковых эллиптических конусов, обращенных друг к другу своими вершинами.
Круглый конус
Площадь боковой поверхности конуса будем рассматривать на примере круглой прямой фигуры. Такой конус представляет собой круглое основание, на которое опирается коническая поверхность. Эта фигура показана ниже.

Все генератрисы этой фигуры равны между собой. Их длина всегда больше радиуса основания. Расстояние от вершины конуса до его круглого основания называется высотой. Высота пересекает круг в его центре, поэтому конус называется прямым.
Получить этот конус не представляет никакой сложности. Для этого следует взять любой треугольник, имеющий прямой угол, и вращать его вокруг одного из катетов так, как показано ниже на схеме.

Если обозначить гипотенузу этого треугольника буквой g, а его катеты h и r, тогда будет справедливо равенство:
g2 = h2 + r2.
Для полученного конуса g — это генератриса, h — высота, r — радиус круга.
Чему равна боковая поверхность конуса с круглым основанием?
Ответить на этот вопрос проще всего, если разрезать коническую поверхность вдоль одной из генератрис и развернуть ее на плоскости. Получившаяся фигура называется разверткой боковой поверхности. Она показана на главном фото к статье, где также приводится круг — основание фигуры.
Эта развертка показывает, что площадь боковой поверхности конуса равна площади соответствующего кругового сектора. Он ограничен двумя генератрисами g, которые представляют радиус полного круга, и дугой. Длина последней точно равна длине окружности основания. Получим формулу для площади этого сектора.
Сначала определим угол в радианах, соответствующий дуге сектора. Его можно найти с использованием следующей пропорции:
2*pi ==> 2*pi*g;
x ==> 2*pi*r.
Здесь 2*pi*g — это длина всей окружности, ограничивающей рассматриваемый сектор, 2*pi*r — это длина дуги сектора. Угол в радианах x сектора будет равен:
x = 2*pi*r*2*pi/(2*pi*g) = 2*pi*r/g.
Для определения площади рассматриваемого сектора, следует воспользоваться пропорцией через соответствующие площади. Имеем:
2*pi ==> pi*g2;
2*pi*r/g ==> Sb.
Здесь pi*g2 является площадью круга, построенного с помощью образующей g, Sb — площадь боковой поверхности конуса, равная площади рассматриваемого кругового сектора. Результатом решения пропорции будет конечная формула для Sb:
Sb = pi*g2*2*pi*r/g/(2*pi) = pi*r*g.
Таким образом, чтобы найти площадь конической поверхности, достаточно умножить радиус фигуры на ее директрису и на число пи.
При получении конечной формулы для Sb через пропорции использовалось свойство равенства угла полной окружности числу 2*pi радиан.
Понятие о конусе усеченном
Пусть имеется круглый прямой конус. Возьмем плоскость и отсечем от этой фигуры верхнюю часть таким образом, чтобы секущая плоскость прошла параллельно основанию конуса. Оставшаяся под плоскостью фигура называется прямым усеченным конусом с параллельными основаниями. Он показан на рисунке ниже.

В отличие от исходной фигуры, усеченный конус образован тремя поверхностями:
- малое круглое основание;
- большое круглое основание;
- часть конической поверхности.
Последняя в списке является боковой поверхностью для рассматриваемой фигуры.
Для усеченной фигуры справедливы те же понятия, что для полного конуса. Так, расстояние между его основаниями — это высота h, каждое основание имеет свой радиус (r1 и r2). Часть генератрисы исходного конуса теперь является генератрисой конуса усеченного. Обозначим ее буквой l.
Между отмеченными линейными параметрами существует следующая связь:
l2 = h2 + (r1-r2)2.
Боковая поверхность усеченной фигуры
Выше было сказано, что представляет собой боковая поверхность для конуса усеченного. Разрезая ее вдоль одной из генератрис, получим следующий результат.

Два круга представляют собой основания. Четырехугольная фигура, ограниченная двумя прямыми отрезками и двумя дугами — это искомая боковая поверхность усеченного конуса, площадь которой необходимо найти. Решим эту задачу.
Заметим, что эта поверхность представляет собой сектор круга, у которого вырезана центральная часть. Обозначим радиус внешней дуги как g. Тогда радиус внутренней дуги будет равен g — l. Используя результаты решения предыдущей пропорции при определении угла сектора x, можно записать следующее равенство:
x = 2*pi*r1/g = 2*pi*r2/(g-l) =>
g = l*r1/(r1-r2).
Искомая площадь Sb равна разнице площадей секторов, построенных с помощью радиусов g и g-l. Используя формулу для площади сектора, полученную выше, можно записать:
Sb = pi*g*r1 — pi*(g-l)*r2.
Подставляя в это выражение формулу для g, получаем конечное равенство для площади боковой поверхности конуса усеченного:
Sb = pi*l*(r1+r2).
Задача на определение площади конической поверхности
Решим простую задачу. Необходимо найти площадь боковой поверхности конуса, если известно, что его высота h равна диаметру основания, а генератриса составляет 15 см.
Запишем соответствующую формулу для Sb, из которой будет видно, какие величины следует рассчитать. Имеем:
Sb = pi*r*g.
Значение генератрисы g известно из условия задачи. Остается определить радиус фигуры.
Генератриса, высота и радиус связаны друг с другом следующим равенством:
g2 = h2 + r2.
Из условия следует, что 2*r = h. Подставляя значение h в выражение, получим:
g2 = (2*r)2 + r2 = 5*r2 =>
r = g/√5.
Теперь формулу для радиуса основания подставляем в выражение для Sb, получаем:
Sb = pi/√5*g2.
Мы получили конечную формулу, из которой видно, что площадь искомой поверхности зависит только от длины генератрисы. Подставляя g = 15 см, получаем ответ на задачу: Sb ≈ 315,96 см2.
Просмотры: 53
Содержание:
Площади поверхностей геометрических тел:
Под площадью поверхности многогранника мы понимаем сумму площадей всех его граней. Как же определить площадь поверхности тела, не являющегося многогранником? На практике это делают так. Разбивают поверхность на такие части, которые уже мало отличаются от плоских. Тогда находят площади этих частей, как будто они являются плоскими. Сумма полученных площадей является приближенной площадью поверхности. Например, площадь крыши здания определяется как сумма площадей кусков листового металла. Еще лучше это видно на примере Земли. Приблизительно она имеет форму шара. Но площади небольших ее участков измеряют так, как будто эти участки являются плоскими. Более того, под площадью поверхности тела будем понимать предел площадей полных поверхностей описанных около него многогранников. При этом должно выполняться условие, при котором все точки поверхности этих многогранников становятся сколь угодно близкими к поверхности данного тела. Для конкретных тел вращения понятие описанного многогранника будет уточнено.
Понятие площади поверхности
Рассмотрим периметры 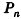
Применим данные соотношения к обоснованию формулы для площади боковой поверхности цилиндра.
При вычислении объема цилиндра были использованы правильные вписанные в него призмы. Найдем при помощи в чем-то аналогичных рассуждений площадь боковой поверхности цилиндра.
Опишем около данного цилиндра радиуса R и высоты h правильную n-угольную призму (рис. 220).
Площадь боковой поверхности призмы равна
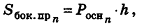
где 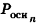 — периметр основания призмы.
— периметр основания призмы.
При неограниченном возрастании n получим:
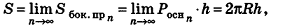
так как периметры оснований призмы стремятся к длине окружности основания цилиндра, то есть к 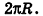
Учитывая, что сумма площадей двух оснований призмы стремится к 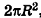 , получаем, что площадь полной поверхности цилиндра равна
, получаем, что площадь полной поверхности цилиндра равна 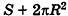 . Но сумма площадей двух оснований цилиндра равна
. Но сумма площадей двух оснований цилиндра равна 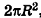 . Поэтому найденную величину S принимают за площадь боковой поверхности цилиндра.
. Поэтому найденную величину S принимают за площадь боковой поверхности цилиндра.
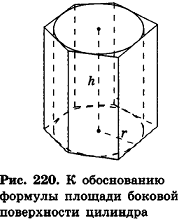
Итак, площадь боковой поверхности цилиндра вычисляется по формуле
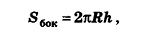
где R — радиус цилиндра, h — его высота.
Заметим, что эта формула аналогична соответствующей формуле площади боковой поверхности прямой призмы 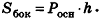
За площадь полной поверхности цилиндра принимается сумма площадей боковой поверхности и двух оснований:
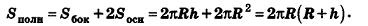
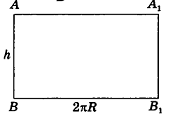
Если боковую поверхность цилиндра радиуса R и высоты h разрезать по образующей АВ и развернуть на плоскость, то в результате получим прямоугольник 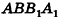 который называется разверткой боковой поверхности цилиндра (рис. 221).
который называется разверткой боковой поверхности цилиндра (рис. 221).
Очевидно, что сторона 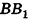 этого прямоугольника есть развертка окружности основания цилиндра, следовательно,
этого прямоугольника есть развертка окружности основания цилиндра, следовательно, 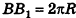 . Сторона АВ равна образующей цилиндра, то есть АВ = h. Значит, площадь развертки боковой поверхности цилиндра равна
. Сторона АВ равна образующей цилиндра, то есть АВ = h. Значит, площадь развертки боковой поверхности цилиндра равна 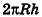 . Таким образом, площадь боковой поверхности цилиндра равна площади ее развертки.
. Таким образом, площадь боковой поверхности цилиндра равна площади ее развертки.

Пример:
Параллельно оси цилиндра на расстоянии d от нее проведена плоскость, отсекающая от основания дугу  . Диагональ полученного сечения наклонена к плоскости основания под углом а. Определите площадь боковой поверхности цилиндра.
. Диагональ полученного сечения наклонена к плоскости основания под углом а. Определите площадь боковой поверхности цилиндра.
Решение:
Пусть дан цилиндр, в основаниях которого лежат равные круги с центрами 
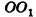 — ось цилиндра. Рассмотрим плоскость, параллельную
— ось цилиндра. Рассмотрим плоскость, параллельную 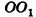 . Сечение цилиндра данной плоскостью представляет собой прямоугольник
. Сечение цилиндра данной плоскостью представляет собой прямоугольник 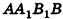 (рис. 222).
(рис. 222).
Пусть хорда АВ отсекает от окружности основания дугу 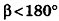 . Тогда, по определению,
. Тогда, по определению, 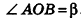 . Так как образующие цилиндра перпендикулярны основаниям,
. Так как образующие цилиндра перпендикулярны основаниям, 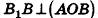 . Значит, АВ — проекция
. Значит, АВ — проекция 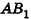 на плоскость АОВ, тогда угол между
на плоскость АОВ, тогда угол между 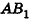 и плоскостью АОВ равен углу
и плоскостью АОВ равен углу 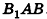 . По условию
. По условию 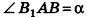 .
.
В равнобедренном треугольнике 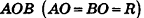 проведем медиану ОК. Тогда O
проведем медиану ОК. Тогда O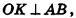
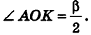 Так как
Так как 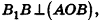 то
то 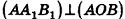 по признаку перпендикулярных плоскостей. Но тогда
по признаку перпендикулярных плоскостей. Но тогда 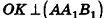 по свойству перпендикулярных плоскостей. Значит, ОК — расстояние между точкой О и плоскостью
по свойству перпендикулярных плоскостей. Значит, ОК — расстояние между точкой О и плоскостью 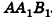 . Учитывая, что
. Учитывая, что 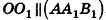 , по определению расстояния между параллельными прямой и плоскостью получаем, что ОК равно расстоянию между
, по определению расстояния между параллельными прямой и плоскостью получаем, что ОК равно расстоянию между 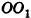 и плоскостью
и плоскостью 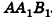 . По условию OK = d. Из прямоугольного треугольника АКО
. По условию OK = d. Из прямоугольного треугольника АКО
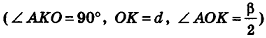 имеем:
имеем: 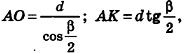
откуда 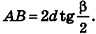 Из прямоугольного треугольника
Из прямоугольного треугольника 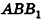
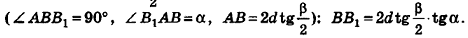
Итак, 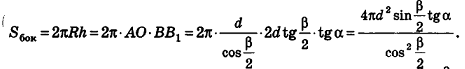
В случае, когда 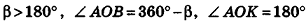
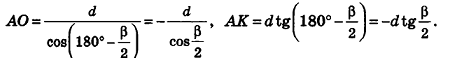
Аналогично предыдущему, и в этом случае получаем тот же результат для площади боковой поверхности.
Ответ:
Площадь поверхности конуса и усеченного конуса
Связь между цилиндрами и призмами полностью аналогична связи между конусами и пирамидами. В частности, это касается формул для площадей их боковых поверхностей.
Опишем около данного конуса с радиусом основания R и образующей I правильную л-угольную пирамиду (рис. 223). Площадь ее боковой поверхности равна
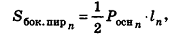
где  — периметр основания пирамиды,
— периметр основания пирамиды,  — апофема.
— апофема.
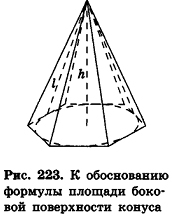
При неограниченном возрастании n получим:
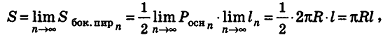
так как периметры оснований пирамиды стремятся к длине окружности основания конуса, а апофемы  равны I.
равны I.
Учитывая, что площадь основания пирамиды стремится к 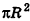 , получаем, что площадь полной поверхности конуса равна
, получаем, что площадь полной поверхности конуса равна 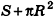 . Но площадь основания конуса равна
. Но площадь основания конуса равна 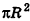 . Поэтому найденную величину S принимают за площадь боковой поверхности конуса. Итак, площадь боковой поверхности конуса вычисляется по формуле
. Поэтому найденную величину S принимают за площадь боковой поверхности конуса. Итак, площадь боковой поверхности конуса вычисляется по формуле
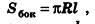
где R — радиус основания, I — образующая.
За площадь полной поверхности конуса принимается сумма площадей его основания и боковой поверхности:
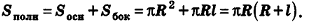
Если боковую поверхность конуса разрезать по образующей РА и развернуть на плоскость, то в результате получим круговой сектор  который называется разверткой боковой поверхности конуса (рис. 224).
который называется разверткой боковой поверхности конуса (рис. 224).
Очевидно, что радиус сектора развертки равен образующей конуса I, а длина дуги  — длине окружности основания конуса, то есть
— длине окружности основания конуса, то есть 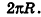 . Учитывая, что площадь соответствующего круга равна
. Учитывая, что площадь соответствующего круга равна 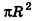 , получаем:
, получаем: 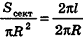 , значит,
, значит, 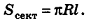 Таким образом, площадь боковой поверхности конуса равна площади ее развертки.
Таким образом, площадь боковой поверхности конуса равна площади ее развертки.
Учитывая формулу для площади боковой поверхности конуса, нетрудно найти площадь боковой поверхности усеченного конуса.
Рассмотрим усеченный конус, полученный при пересечении конуса с вершиной Р некоторой секущей плоскостью (рис. 225).
Пусть 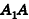 — образующая усеченного конуса
— образующая усеченного конуса 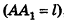 точки
точки  — центры большего и меньшего оснований с радиусами R и г соответственно. Тогда площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей двух конусов:
— центры большего и меньшего оснований с радиусами R и г соответственно. Тогда площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей двух конусов:
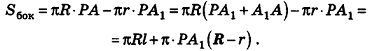
Из подобия треугольников 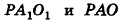
следует, что 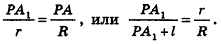
Тогда получаем 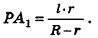
Таким образом, 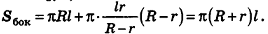
Итак, мы получили формулу для вычисления площади боковой поверхности усеченного конуса: 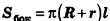 , где R и г — радиусы оснований усеченного конуса, I — его образующая.
, где R и г — радиусы оснований усеченного конуса, I — его образующая.
Отсюда ясно, что площадь полной поверхности усеченного конуса равна 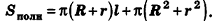
Такой же результат можно было бы получить, если найти площадь развертки боковой поверхности усеченного конуса или использовать правильные усеченные пирамиды, описанные около него. Попробуйте дать соответствующие определения и провести необходимые рассуждения самостоятельно.
Связь между площадями поверхностей и объемами
При рассмотрении объемов и площадей поверхностей цилиндра и конуса мы видели, что существует тесная взаимосвязь между этими фигурами и призмами и пирамидами соответственно. Оказывается, что и сфера (шар), вписанная в многогранник, связана с величиной его объема.
Определение:
Сфера (шар) называется вписанной в выпуклый многогранник, если она касается каждой его грани.
При этом многогранник называется описанным около данной сферы (рис. 226).
Рассмотрим, например, сферу, вписанную в тетраэдр (рис. 227).
Плоскости, содержащие грани тетраэдра, являются касательными к вписанной сфере, а точки касания лежат в гранях тетраэдра. Заметим, что по доказанному в п. 14.2 радиусы вписанной сферы, проведенные в точку касания с поверхностью многогранника, перпендикулярны плоскостям граней этого многогранника.
Для описанных многоугольников на плоскости было доказано, что их площадь равна произведению полупериметра на радиус вписанной окружности. Аналогичное свойство связывает объем описанного многогранника и площадь его поверхности.
Теорема (о связи площади поверхности и объема описанного многогранника)
Объем описанного многогранника вычисляется по формуле
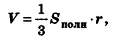
где  — площадь полной поверхности многогранника, г — радиус вписанной сферы.
— площадь полной поверхности многогранника, г — радиус вписанной сферы.
Доказательство:
Соединим центр вписанной сферы О со всеми вершинами многогранника  (рис. 228). Получим n пирамид, основаниями которых являются грани многогранника, вершины совпадают с точкой О, высоты равны г. Тогда объем многогранника, по аксиоме, равен сумме объемов этих пирамид. Используя формулу объема пирамиды, найдем объем данного многогранника:
(рис. 228). Получим n пирамид, основаниями которых являются грани многогранника, вершины совпадают с точкой О, высоты равны г. Тогда объем многогранника, по аксиоме, равен сумме объемов этих пирамид. Используя формулу объема пирамиды, найдем объем данного многогранника:
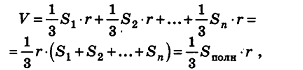
где 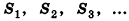 – площади граней многогранника.
– площади граней многогранника.
Теорема доказана.
Оказывается, что в любой тетраэдр можно вписать сферу, и только одну. Но не каждый выпуклый многогранник обладает этим свойством.
Рассматривают также сферы, описанные около многогранника.
Определение:
Сфера называется описанной около многогранника, если все его вершины лежат на сфере.
При этом многогранник называется вписанным в сферу (рис. 229).
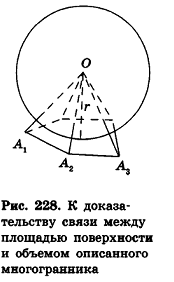
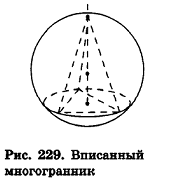
Также считается, что соответствующий шар описан около многогранника.
Около любого тетраэдра можно описать единственную сферу, но не каждый многогранник обладает соответствующим свойством.
Площадь сферы
Применим полученную связь для объемов и площадей поверхностей описанных многогранников к выводу формулы площади сферы.
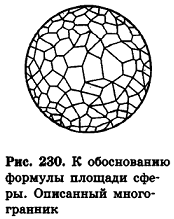
Опишем около сферы радиуса R выпуклый многогранник (рис. 230).
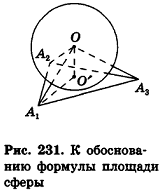
Пусть S’ — площадь полной поверхности данного многогранника, а любые две точки одной грани удалены друг от друга меньше чем на е. Тогда объем многогранника равен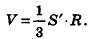 . Рассмотрим расстояние от центра сферы О до любой вершины многогранника, например А1 (рис. 231).
. Рассмотрим расстояние от центра сферы О до любой вершины многогранника, например А1 (рис. 231).
По неравенству треугольника 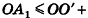
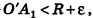 где О’ — точка касания. Отсюда следует, что все вершины данного многогранника лежат внутри шара с центром О и радиусом
где О’ — точка касания. Отсюда следует, что все вершины данного многогранника лежат внутри шара с центром О и радиусом 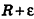 .
.
Итак, объем V данного многогранника больше объема шара радиуса R и меньше объема шара радиуса 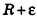 , то есть
, то есть 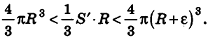
Отсюда получаем 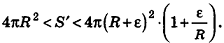
Если неограниченно уменьшать размеры граней многогранника, то есть при е, стремящемся к нулю, левая и правая части последнего неравенства будут стремиться к 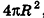 , а многогранник все плотнее примыкать к сфере. Поэтому полученную величину для предела S’ принимают за площадь сферы.
, а многогранник все плотнее примыкать к сфере. Поэтому полученную величину для предела S’ принимают за площадь сферы.
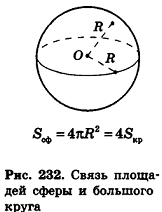
Итак, площадь сферы радиуса R вычисляется по формуле 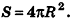
Доказанная формула означает, что площадь сферы равна четырем площадям ее большого круга (рис. 232).
Исходя из аналогичных рассуждений, можно получить формулу для площади сферической части шарового сегмента с высотой Н:
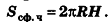
Оказывается, что эта формула справедлива и для площади сферической поверхности шарового слоя (пояса):
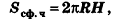
где Н — высота слоя (пояса).
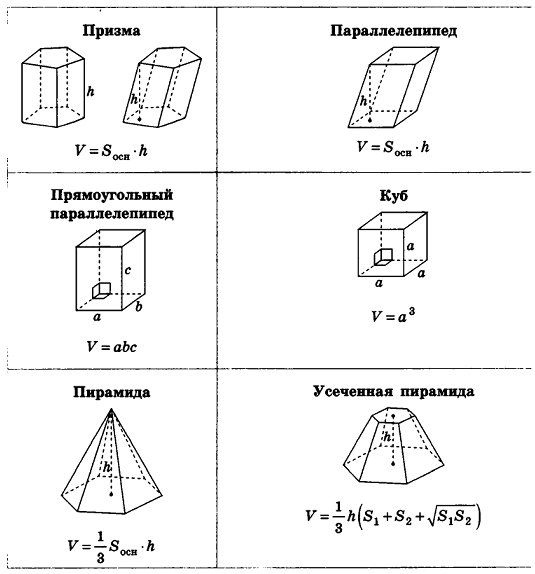
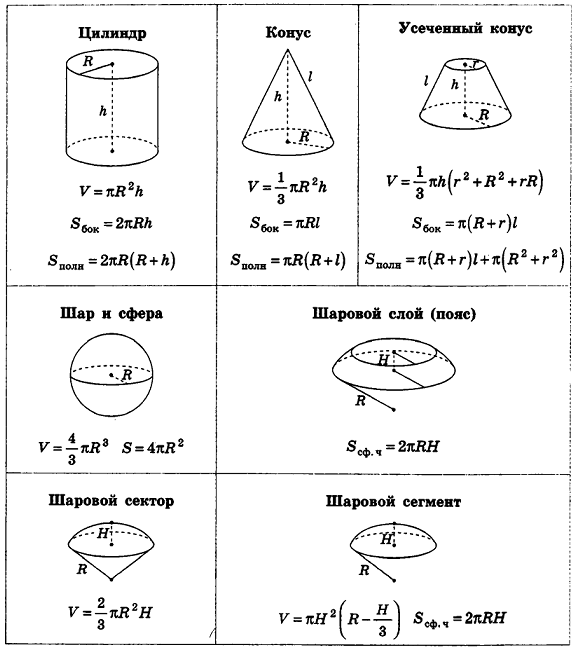
Справочный материал
Формулы объемов и площадей поверхностей геометрических тел
Историческая справка
Многие формулы для вычисления объемов многогранников были известны уже в Древнем Египте. В так называемом Московском папирусе, созданном около 4000 лет назад, вероятно, впервые в истории вычисляется объем усеченной пирамиды. Но четкие доказательства большинства формул для объемов появились позднее, в работах древнегреческих ученых.
Так, доказательства формул для объемов конуса и пирамиды связаны с именами Демокрита из Абдеры (ок. 460-370 гг. до н. э.) и Евдокса Книдского (ок. 408-355 гг. до н. э.). На основании их идей выдающийся математик и механик Архимед (287-212 гг. до н. э.) вычислил объем шара, нашел формулы для площадей поверхностей цилиндра, конуса, сферьГг
Дальнейшее развитие методы, предложенные Архимедом, получили благодаря трудам средневекового итальянского монаха и математика Бонавентуры Кавальери (1598-1647). В своей книге «Геометрия неделимых» он сформулировал принцип сравнения объемов, при котором используются площади сечений. Его рассуждения стали основой интегральных методов вычисления объемов, разработанных Исааком Ньютоном (1642 (1643)-1727) и Готфридом Вильгельмом фон Лейбницем (1646-1716). Во многих учебниках по геометрии объем пирамиды находится с помощью * чертовой лестницы» — варианта древнегреческого метода вычерпывания, предложенного французским математиком А. М. Лежандром (1752-1833).


На II Международном конгрессе математиков, который состоялся в 1900 году в Париже, Давид Гильберт сформулировал, в частности, такую проблему: верно ли, что любые два равновеликих многогранника являются равносоставленными? Уже через год отрицательный ответ на этот вопрос был обоснован учеником Гильберта Максом Деном (1878-1952). Другое доказательство этого факта предложил в 1903 году известный геометр В. Ф. Каган, который в начале XX века вел плодотворную научную и просветительскую деятельность в Одессе. В частности, из работ Дена и Кагана следует, что доказательство формулы объема пирамиды невозможно без применения пределов.
Весомый вклад в развитие теории площадей поверхностей внесли немецкие математики XIX века. Так, в 1890 году Карл Герман Аман-дус Шварц (1843-1921) построил пример последовательности многогранных поверхностей, вписанных в боковую поверхность цилиндра («сапог Шварца»). Уменьшение их граней не приводит к приближению суммы площадей этих граней к площади боковой поверхности цилиндра. Это стало толчком к созданию выдающимся немецким математиком и физиком Германом Минков-ским (1864-1909) современной теории площадей поверхностей, в которой последние связаны с объемом слоя около данной поверхности.
Учитывая огромный вклад Архимеда в развитие математики, в частности теории объемов и площадей поверхностей, именно его изобразили на Филдсовской медали — самой почетной в мире награде для молодых математиков. В 1990 году ею был награжден Владимир Дрин-фельд (род. в 1954 г.), который учился и некоторое время работал в Харькове. Вот так юные таланты, успешно изучающие геометрию в школе, становятся в дальнейшем всемирно известными учеными.




Уравнения фигур в пространстве
Напомним, что уравнением фигуры F на плоскости называется уравнение, которому удовлетворяют координаты любой точки фигуры F и не удовлетворяют координаты ни одной точки, не принадлежащей фигуре F. Так же определяют и уравнение фигуры в пространстве; но, в отличие от плоскости, где уравнение фигуры содержит две переменные х и у, в пространстве уравнение фигуры является уравнением с тремя переменными х, у и z.
Выведем уравнение плоскости, прямой и сферы в пространстве. Для получения уравнения плоскости рассмотрим в прямоугольной системе координат плоскость а (рис. 233) и определим свойство, с помощью которого можно описать принадлежность произвольной точки данной плоскости. Пусть ненулевой вектор 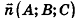 перпендикулярен а (то есть принадлежит прямой, перпендикулярной данной плоскости,— такой вектор называют вектором нормали или нормалью к плоскости а), а точка
перпендикулярен а (то есть принадлежит прямой, перпендикулярной данной плоскости,— такой вектор называют вектором нормали или нормалью к плоскости а), а точка 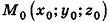 принадлежит данной плоскости.
принадлежит данной плоскости.
Так как 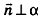 , то вектор га перпендикулярен любому вектору плоскости а. Поэтому если
, то вектор га перпендикулярен любому вектору плоскости а. Поэтому если 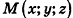 — произвольная точка плоскости а, то
— произвольная точка плоскости а, то 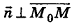 , то есть
, то есть 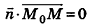 . Более того, если векторы
. Более того, если векторы 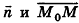 перпендикулярны, то, поскольку плоскость, проходящая через точку М0 перпендикулярно вектору
перпендикулярны, то, поскольку плоскость, проходящая через точку М0 перпендикулярно вектору 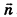 , единственна, имеем
, единственна, имеем 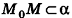 , то есть
, то есть 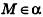 . Таким образом, уравнение
. Таким образом, уравнение 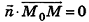 — критерий принадлежности точки М плоскости а. На основании этого векторного критерия выведем уравнение плоскости в пространстве.
— критерий принадлежности точки М плоскости а. На основании этого векторного критерия выведем уравнение плоскости в пространстве.
Теорема (уравнение плоскости в пространстве)
В прямоугольной системе координат уравнение плоскости имеет вид 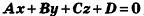 , где А, В, С и D — некоторые числа, причем числа А, В и С одновременно не равны нулю.
, где А, В, С и D — некоторые числа, причем числа А, В и С одновременно не равны нулю.
Доказательство:
Запишем в координатной форме векторное равенство 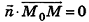 , где
, где 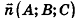 — вектор нормали к данной плоскости,
— вектор нормали к данной плоскости, 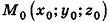 — фиксированная точка плоскости, M(x;y;z) — произвольная точка плоскости. Имеем
— фиксированная точка плоскости, M(x;y;z) — произвольная точка плоскости. Имеем 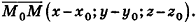
Следовательно, 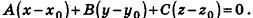
После раскрытия скобок и приведения подобных членов это уравнение примет вид: 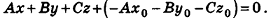
Обозначив числовое выражение в скобках через D, получим искомое уравнение, в котором числа А, В и С одновременно не равны нулю, так как 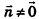 .
.
Покажем теперь, что любое уравнение вида Ах + Ву +Cz+D = 0 задает в пространстве плоскость. Действительно, пусть 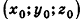 — одно из решений данного уравнения. Тогда
— одно из решений данного уравнения. Тогда 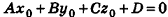 . Вычитая это равенство из данного, получим
. Вычитая это равенство из данного, получим 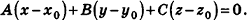 Так как это уравнение является координатной записью векторного равенства
Так как это уравнение является координатной записью векторного равенства 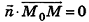 , то оно является уравнением плоскости, проходящей через точку
, то оно является уравнением плоскости, проходящей через точку 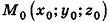 перпендикулярно вектору
перпендикулярно вектору 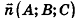 .
.
Обратим внимание на то, что в доказательстве теоремы приведен способ составления уравнения плоскости по данным координатам произвольной точки плоскости и вектора нормали.
Пример:
Напишите уравнение плоскости, которая перпендикулярна отрезку MN и проходит через его середину, если М{-1;2;3), N(5;-4;-1).
Решение:
Найдем координаты точки О — середины отрезка MN:
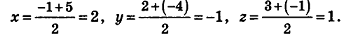
Значит, О (2; -1; l). Так как данная плоскость перпендикулярна отрезку MN, то вектор 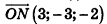 — вектор нормали к данной плоскости. Поэтому искомое уравнение имеет вид:
— вектор нормали к данной плоскости. Поэтому искомое уравнение имеет вид: 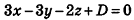 .
.
И наконец, так как данная плоскость проходит через точку О(2;-l;l), то, подставив координаты этой точки в уравнение, получим: 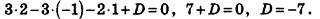
Таким образом, уравнение 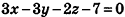 искомое.
искомое.
Ответ: 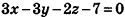
Заметим, что правильным ответом в данной задаче является также любое уравнение, полученное из приведенного умножением обеих частей на число, отличное от нуля.
Значения коэффициентов А, В, С и D в уравнении плоскости определяют особенности расположения плоскости в системе координат. В частности:
- если
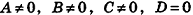 , уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);
, уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а); - если один из коэффициентов А, В и С равен нулю, a
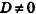 , плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали
, плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали 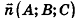 перпендикулярен оси Ох, а плоскость By + Cz + D = Q параллельна оси Ох (рис. 234, б)
перпендикулярен оси Ох, а плоскость By + Cz + D = Q параллельна оси Ох (рис. 234, б) - если два из коэффициентов А, В и С равны нулю, а
 , плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали
, плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали 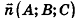 перпендикулярен плоскости Оху, а плоскость Cz+D = 0 параллельна плоскости Оху (рис. 234, в);
перпендикулярен плоскости Оху, а плоскость Cz+D = 0 параллельна плоскости Оху (рис. 234, в); - если два из коэффициентов А, В и С равны нулю и D = 0, плоскость совпадает с одной из координатных плоскостей: например, при условиях
 и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
Предлагаем вам самостоятельно составить полную таблицу частных случаев расположения плоскости Ax + By+Cz+D = 0 в прямоугольной системе координат в зависимости от значений коэффициентов А, В, С и D.
Пример: (о расстоянии от точки до плоскости)
Расстояние от точки 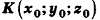 до плоскости а, заданной уравнением Ax + By + Cz+D = О, вычисляется по формуле
до плоскости а, заданной уравнением Ax + By + Cz+D = О, вычисляется по формуле
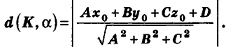 Докажите.
Докажите.
Решение:
Если 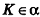 , то по уравнению плоскости
, то по уравнению плоскости 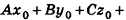
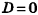 , откуда
, откуда 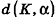 = 0.
= 0.
Если 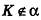 , то проведем перпендикуляр КМ к плоскости a,
, то проведем перпендикуляр КМ к плоскости a, 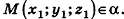 .
.
Тогда 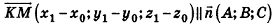 , поэтому
, поэтому 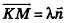 , то есть
, то есть 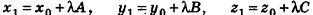 . Так как
. Так как 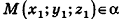 , то
, то 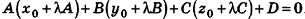 , откуда
, откуда 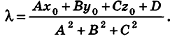
Таким образом, 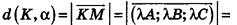
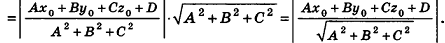
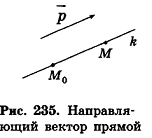
Рассмотрим теперь возможность описания прямой в пространстве с помощью уравнений.
Пусть в пространстве дана прямая k (рис. 235). Выберем ненулевой вектор 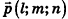 , параллельный данной прямой или принадлежащий ей (такой вектор называют направляющим вектором прямой k), и зафиксируем точку
, параллельный данной прямой или принадлежащий ей (такой вектор называют направляющим вектором прямой k), и зафиксируем точку 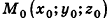 , принадлежащую данной прямой. Тогда произвольная точка пространства М (х; у; z) будет принадлежать прямой k в том и только в том случае, когда векторы
, принадлежащую данной прямой. Тогда произвольная точка пространства М (х; у; z) будет принадлежать прямой k в том и только в том случае, когда векторы 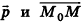 коллинеарны, то есть существует число t такое, что
коллинеарны, то есть существует число t такое, что 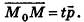
Представим это векторное равенство в координатной форме. Если ни одна из координат направляющего вектора не равна нулю, из данного равенства можно выразить t и приравнять полученные результаты:
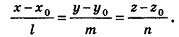
Эти равенства называют каноническими уравнениями прямой в пространстве.
Пример:
Напишите уравнение прямой, проходящей через точки А(1;-3;2) и В(-l;0;l).
Решение:
Так как точки А и В принадлежат данной прямой, то 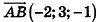 — направляющий вектор прямой АВ. Таким образом, подставив вместо
— направляющий вектор прямой АВ. Таким образом, подставив вместо  координаты точки А, получим уравнение прямой АВ:
координаты точки А, получим уравнение прямой АВ:
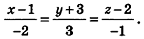
Ответ: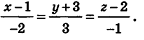
Заметим, что ответ в этой задаче может иметь и другой вид: так, в числителях дробей можно использовать координаты точки В, а как направляющий вектор рассматривать любой ненулевой вектор, коллинеарный 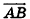 (например, вектор
(например, вектор 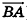 ).
).
Вообще, если прямая в пространстве задана двумя точками 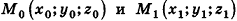 , то
, то 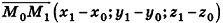 — направляющий вектор прямой, а в случае, если соответствующие координаты данных точек не совпадают, канонические уравнения прямой
— направляющий вектор прямой, а в случае, если соответствующие координаты данных точек не совпадают, канонические уравнения прямой 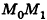 имеют вид
имеют вид 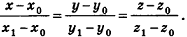
С помощью уравнений удобно исследовать взаимное расположение прямых и плоскостей в пространстве. Рассмотрим прямые  направляющими векторами
направляющими векторами 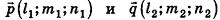 соответственно. Определение угла между данными прямыми связано с определением угла между их направляющими векторами. Действительно, пусть ф — угол между прямыми
соответственно. Определение угла между данными прямыми связано с определением угла между их направляющими векторами. Действительно, пусть ф — угол между прямыми 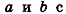 . Так как по определению
. Так как по определению  , а угол между векторами может быть больше 90°, то
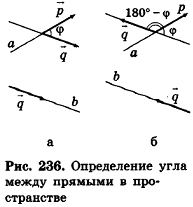
, а угол между векторами может быть больше 90°, то 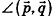 либо равен углу ср (рис. 236, а), либо дополняет его до 180° (рис. 236, б).
либо равен углу ср (рис. 236, а), либо дополняет его до 180° (рис. 236, б).
Так как cos(l80°-ф) = -coscp, имеем 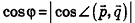 , то есть
, то есть
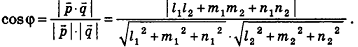
Отсюда, в частности, следует необходимое и достаточное условие перпендикулярности прямых  :
:
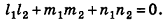
Кроме того, прямые 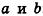 параллельны тогда и только тогда, когда их направляющие векторы коллинеарны, то есть существует число t такое, что
параллельны тогда и только тогда, когда их направляющие векторы коллинеарны, то есть существует число t такое, что 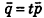 , или, при условии отсутствия у векторов р и q нулевых координат,
, или, при условии отсутствия у векторов р и q нулевых координат,
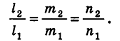
Проанализируем теперь отдельные случаи взаимного расположения двух плоскостей в пространстве. Очевидно, что если 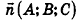 —вектор нормали к плоскости а, то все ненулевые векторы, коллинеарные л, также являются векторами нормали к плоскости а. Из этого следует, что две плоскости, заданные уравнениями
—вектор нормали к плоскости а, то все ненулевые векторы, коллинеарные л, также являются векторами нормали к плоскости а. Из этого следует, что две плоскости, заданные уравнениями 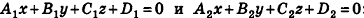 :
:
- совпадают, если существует число t такое, что
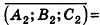
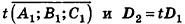 , или, если числа
, или, если числа 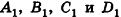 ненулевые
ненулевые 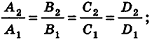
- параллельны, если существует число t такое, что
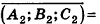
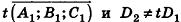 , или, если координаты
, или, если координаты 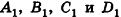 ненулевые,
ненулевые, 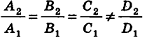 (на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где
(на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где 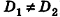 ).
).
В остальных случаях данные плоскости  пересекаются, причем угол между ними связан с углом между векторами нормалей
пересекаются, причем угол между ними связан с углом между векторами нормалей 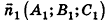 и
и 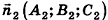 . Предлагаем вам самостоятельно обосновать формулу для определения угла между плоскостями
. Предлагаем вам самостоятельно обосновать формулу для определения угла между плоскостями 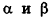 :
:
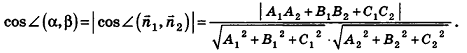
В частности, необходимое и достаточное условие перпендикулярности плоскостей 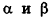 выражается равенством
выражается равенством 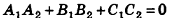 .
.
Заметим также, что прямая в пространстве может быть описана как линия пересечения двух плоскостей, то есть системой уравнений
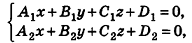
где векторы 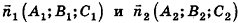 не коллинеарны.
не коллинеарны.
Пример:
Напишите уравнение плоскости, которая проходит через точку М(4;2;3) и параллельна плоскости x-y + 2z-S = 0.
Решение:
Так как искомая плоскость параллельна данной, то вектор нормали к данной плоскости 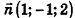 является также вектором нормали к искомой плоскости. Значит, искомое уравнение имеет вид
является также вектором нормали к искомой плоскости. Значит, искомое уравнение имеет вид 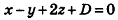 . Так как точка М принадлежит искомой плоскости, ее координаты удовлетворяют уравнению плоскости, то есть 4-2 + 2-3 + 2) = 0, D = -8. Следовательно, уравнение x-y+2z-8=0 искомое.
. Так как точка М принадлежит искомой плоскости, ее координаты удовлетворяют уравнению плоскости, то есть 4-2 + 2-3 + 2) = 0, D = -8. Следовательно, уравнение x-y+2z-8=0 искомое.
Ответ: x-y+2z-8 = 0.
Аналогично уравнению окружности на плоскости, в пространственной декартовой системе координат можно вывести уравнение сферы с заданным центром и радиусом.
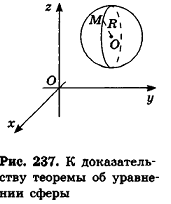
Теорема (уравнение сферы)
В прямоугольной системе координат уравнение сферы радиуса R с центром в точке 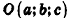 имеет вид
имеет вид 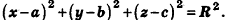 Доказательство
Доказательство
Пусть 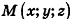 — произвольная точка сферы радиуса R с центром
— произвольная точка сферы радиуса R с центром 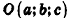 (рис. 237). Расстояние между точками О и М вычисляется по формуле
(рис. 237). Расстояние между точками О и М вычисляется по формуле 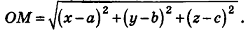
Так как OM=R, то есть ОМ2 = R2, то координаты точки М удовлетворяют уравнению 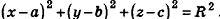 . Если же точка М не является точкой сферы, то
. Если же точка М не является точкой сферы, то 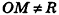 , значит, координаты точки М не удовлетворяют данному уравнению.
, значит, координаты точки М не удовлетворяют данному уравнению.
Следствие
Сфера радиуса R с центром в начале координат задается уравнением вида
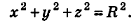
Заметим, что фигуры в пространстве, как и на плоскости, могут задаваться не только уравнениями, но и неравенствами. Например, шар радиуса R с центром в точке 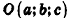 задается неравенством
задается неравенством 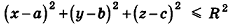 (убедитесь в этом самостоятельно).
(убедитесь в этом самостоятельно).
Пример:
Напишите уравнение сферы с центром А (2;-8; 16), которая проходит через начало координат.
Решение:
Так как данная сфера проходит через точку 0(0;0;0), то отрезок АО является ее радиусом. Значит,
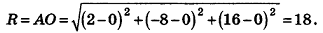
Таким образом, искомое уравнение имеет вид:
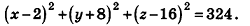
Ответ: 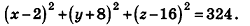
Доказательство формулы объема прямоугольного параллелепипеда
Теорема (формула объема прямоугольного параллелепипеда)
Объем прямоугольного параллелепипеда равен произведению трех его измерений:
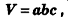
где 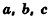 — измерения параллелепипеда.
— измерения параллелепипеда.
Доказательство:
Докажем сначала, что объемы двух прямоугольных параллелепипедов с равными основаниями относятся как длины их высот.
Пусть 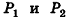 — два прямоугольных параллелепипеда с равными основаниями и объемами
— два прямоугольных параллелепипеда с равными основаниями и объемами 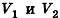 соответственно. Совместим данные параллелепипеды. Для этого достаточно совместить их основания. Теперь рассмотрим объемы параллелепипедов
соответственно. Совместим данные параллелепипеды. Для этого достаточно совместить их основания. Теперь рассмотрим объемы параллелепипедов 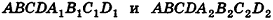 (рис. 238). Для определенности будем считать, что
(рис. 238). Для определенности будем считать, что 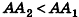 . Разобьем ребро
. Разобьем ребро 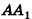 на n равных отрезков. Пусть на отрезке
на n равных отрезков. Пусть на отрезке 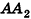 лежит m точек деления. Тогда:
лежит m точек деления. Тогда:
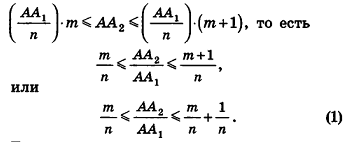
проведем через точки деления параллельные основанию ABCD (рис. 239). Они разобьют параллелепипед 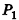 на n равных параллелепипедов. Каждый из них имеет объем
на n равных параллелепипедов. Каждый из них имеет объем  . Очевидно, что параллелепиппед
. Очевидно, что параллелепиппед  содержит в себе объединение m параллелепипедов и сам содержится в объединении
содержит в себе объединение m параллелепипедов и сам содержится в объединении 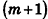 параллелепипедов.
параллелепипедов.
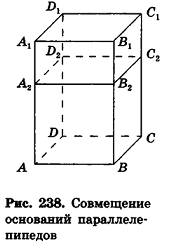
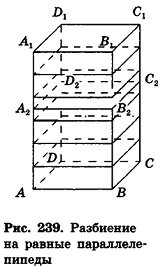
Таким образом, 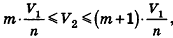 откуда
откуда 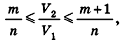 или
или 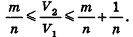
Сравнивая выражения (1) и (2), видим, что оба отношения  находятся между
находятся между  , то есть отличаются не больше чем на
, то есть отличаются не больше чем на 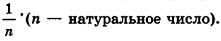 Докажем методом от противного, что эти отношения равны.
Докажем методом от противного, что эти отношения равны.
Допустим, что это не так, то есть 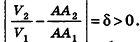 Тогда найдется такое натуральное число n, что
Тогда найдется такое натуральное число n, что 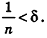 Отсюда
Отсюда 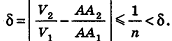 Из полученного противоречия следует, что
Из полученного противоречия следует, что 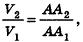 то есть объемы двух прямоугольных параллелепипедов с равными основаниями относятся как длины их высот.
то есть объемы двух прямоугольных параллелепипедов с равными основаниями относятся как длины их высот.
Рассмотрим теперь прямоугольные параллелепипеды с измерениями 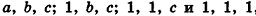 объемы которых равны V,
объемы которых равны V,  соответственно (рис. 240).
соответственно (рис. 240).
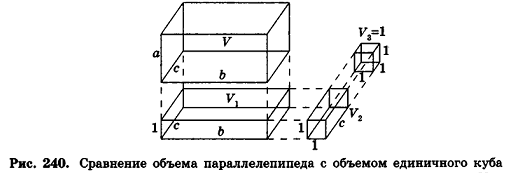
По аксиоме объема V3 =1. По доказанному 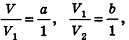
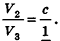 Перемножив эти отношения, получим: V = abc.
Перемножив эти отношения, получим: V = abc.
Теорема доказана.
* Выберем 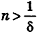 , например,
, например, 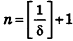 , где
, где 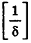 — целая часть дроби
— целая часть дроби 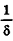 .
.
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии
- Многоугольник
- Площадь многоугольника
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Площади фигур в геометрии
