Как найти площадь развертки тетраэдра

Добрый
день! Мы продолжаем с вами изучать тему: «Параллельность прямых и
плоскостей».

Кристаллическая
решетка метана

Тетрапакет
для молока

Любимая
игрушка моего детства Кубик Рубика

Уголковый
отражатель

Я думаю,
уже понятно, что сегодня речь пойдет о многогранниках- поверхностях
геометрических тел, составленных из многоугольников.

текст

Многоугольник-
часть плоскости, ограниченная замкнутой линией без самопересечений, включая
ее саму.

Необходим вот такой рисунок с пояснениями или чертеж
треугольника.

Картинка

А именно
о тетраэдре.

Нужна анимационная картинка тетраэдра, которая вращается, грани
раскрашены в разные оттенки зеленого цвета.

ТЕТРА́ЭДР [фр. tétraèdre
< греч. tetra четыре + hedra сторона, основание]. геом. Четырехгранник, треугольная пирамида.

(пауза)

Проводить
изучение многогранников будем по плану:

1. определение
тетраэдра

2. элементы
тетраэдра

3. развертка
тетраэдра

4. изображение
на плоскости

План
изучения многогранников:

1. определение
тетраэдра

2. элементы
тетраэдра

3. развертка
тетраэдра

4. изображение
на плоскости

1. построим
треугольник АBC

2. точка D, не
лежащая в плоскости этого треугольника

3. соединяем
точку D
отрезками с вершинами треугольника ABC. Получим
треугольники DAB, DBC и DCA.

Пошагово
появляется чертеж

(пауза)

Определение:
Поверхность составленная из четырех треугольников АBC, DAB, DBC и DCA
называется тетраэдром.

Обозначение: DABC.

Определение:
Поверхность составленная из четырех треугольников АBC, DAB, DBC и DCA
называется тетраэдром.

Обозначение: DABC.

(Пауза)

Элементы
тетраэдра

Треугольники,
из которых состоит тетраэдр, называются гранями, их стороны ребрами, а
вершины – вершинами тетраэдра.

Сколько
граней, ребер и вершин имеет тетраэдр?

Желательно
чтобы появился предыдущий рисунок и элементы подписывались на чертеже и
указывались стрелочками по мере их прочтения.

(пауза)

Тетраэдр
имеет четыре грани, шесть ребер и четыре вершины

Два
ребра тетраэдра, не имеющие общих вершин, называются противоположными.

На рисунке противоположными являются
ребра AD
и BC,
BD
и AC,
CD
и AB

Появляется
предыдущий рисунок, по мере чтения текста цветом на рисунке выделяются
противоположные вершины

Текст

противоположными ребра AD
и BC,
BD
и AC,
CD
и AB

Иногда выделяют
одну из граней тетраэдра и называют ее основанием, а три другие – боковыми
гранями.

Развертка
тетраэдра.

Для изготовления тетраэдра из бумаги вам
потребуется следующая развертка,

ее нужно перенести на плотную бумагу,
вырезать, согнуть по пунктирным линиям и склеить.

На
экране появляется развертка тетраэдра.

На
плоскости тетраэдр изображается

В виде
выпуклого или невыпуклого четырехугольника с диагоналями. При этом штриховыми
линиями изображаются невидимые ребра.

На
первом рисунке AC–
невидимое ребро,

на
втором – EK, LK и KF.

Изображение
тетраэдра на плоскости:

Решим
несколько типовых задач на тетраэдр:

Задача
1.

Найти
площадь развертки правильного тетраэдра с ребром 5 см.

Решение.
Начертим развертку тетраэдра

(на
экране появляется развертка тетраэдра )

Данный тетраэдр состоит из четырех
равносторонних треугольников, следовательно, площадь развертки правильного
тетраэдра равна площади полной поверхности тетраэдра или площади четырех
правильных треугольников.

Площадь
правильного треугольника ищем по формуле:

Задача
1.
Найти площадь развертки правильного тетраэдра с ребром 5 см.

Площадь
правильного треугольника:

Тогда
получаем площадь тетраэдра равна:

Подставим
в формулу длину ребра а=5 см,

получается

Ответ: Площадь развертки правильного
тетраэдра

Площадь
полной поверхности правильного тетраэдра

Задача 2

Постройте
сечение тетраэдра плоскостью проходящей через точки M, N и K.

Задача 2

Постройте
сечение тетраэдра плоскостью проходящей через точки M, N и K.

б)

а)
Действительно, соединим точки M и N (принадлежат
грани ADC),
точки M и K(принадлежат
грани ADB),
точки N и K (грани DBC).
Сечением тетраэдра является треугольник MKN.

а)

б) Соединим точки M
и K
(принадлежат грани ADB),
точки K и N(принадлежат
грани DCB),
далее прямые MK и AB
продолжить до пересечения и поставить точку P.
Прямая PN и точка T
лежат в одной плоскости АВС и теперь можно построить пересечение прямой МК с
каждой гранью. В результате получается четырехугольник MKNT,
который является искомым сечением.

б) (Построение желательно делать поэтапно со словами
диктора)

Источник

Тема: Площадь развертки тетраэдра. (Прочитано 2751 раз)

0 Пользователей и 1 Гость просматривают эту тему.

Вашему вниманию предлагается задача из области стереометрии!
Длина ребра правильного тетраэдра 5 см,найдите площадь развертки тетраэдра.
S развертки правильного тетраэдра 36√3.
Найдите длину ребра?
Помогите ,умоляю вас!!! ::)Жду с нетерпением

« Последнее редактирование: 17 Апреля 2012, 13:41:48 от Белый кролик »

УчениГ ))

« Последнее редактирование: 10 Сентября 2009, 21:37:05 от Asix »

Пожалуйста не пишите голое условие! Сначало мы выслушаем Ваши мысли или хотябы вопросы, но конкретные и лишь потом дадим необходимые советы!
Но можете всего этого и не делать, если Вас не интересует результат
Если не хотите разбираться сами закажите решение на сайте.

Сколько у него граней и что они представляют из себя? Каковы они у правильного тетраэдра?

« Последнее редактирование: 10 Сентября 2009, 21:37:12 от Asix »

Я тоже жду с нетерпением ответа)) Как только дождусь, тронемся в решении дальше)

« Последнее редактирование: 10 Сентября 2009, 21:37:19 от Asix »

Надеюсь Вы теорию по стереометри подняли?
Какие есть свои идеи и наработки?
Ждем ТС и будем решать вместе =))

Я уже связался с ним по аське) Несет черти что, и требует не помощи, а халявы. Я задаю вопросы по теории, а он спрашивает: так вы что сами не знаете))))

Я тоже отправил его на поиски теории)) Он сказал, что развертака – это трехмерная модель и прочее) Ну я и отправил его за теорией))

Как показывает опыт, такие люди есть, но халявщиков становиться с каждым днем все меньше =))
Мы не решаем за Вас, мы помогает понять =))

Источник

В данной публикации мы рассмотрим определение и разновидности тетраэдра, а также формулы для расчета площади его поверхности (одной грани и полной) и объема. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение тетраэдра
Виды тетраэдра
Формулы площади и объема правильного тетраэдра

Определение тетраэдра

Тетраэдр – это разновидность пирамиды; четырехгранник, гранями которого являются треугольники.

Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Каждая грань фигуры может быть ее основанием.

Развертка тетраэдра на примере правильной фигуры представлена ниже:

Основные элементы и свойства тетраэдра (к нему применимы свойства правильной пирамиды) мы рассмотрели в отдельной публикации.

Виды тетраэдра

Равногранный тетраэдр – боковые грани фигуры равны, а основанием является правильный (равносторонний) треугольник.
Прямоугольный тетраэдр – угол между всеми тремя ребрами при одной вершине является прямым, т.е. равным 90°.
Правильный тетраэдр – все ребра равны, а грани, соответственно, являются равносторонними треугольниками.
Ортоцентричный тетраэдр – все высоты, проведенные из всех вершин фигуры к противолежащим граням, пересекаются в одной точке.

Формулы площади и объема правильного тетраэдра

Площадь поверхности

Объем

Источник

Как начертить правильный тетраэдр (5 класс)?

Как легко и быстро начертить правильный тетраэдр? Задание для 5 класса.

Тетраэдр — это разновидность многогранника, состоящая из четырех граней,являющихся треугольниками,в каждой вершине должно сойтись три грани. Правильным называется если у него все грани являюся правильными треугольниками, двугранные углы при ребрах и все трехгранные углы на вершинах равны. Для построения сначала строим куб- это правильный многогранник у которого каждая грань является квадратом. в любом построенном квадрате берем одну вершину (А)и к ней сводим три квадратные грани куба.Каждую грань отмечаем буквами -это вершины(В,С,D).Отрезки которые получились AB, AC, AD, BC, DC, BD они равные между собой,следовательно фигура ABCD является правильным тетрадэром.

Как построить тетраэдр

Тетраэдр – это одна разновидностей многогранника, он состоит из четырёх граней, являющихся треугольниками, в каждой вершине тетраэдра сходятся по три грани. Тетраэдр называется правильным, если все его грани являются правильными треугольниками, все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны.

Для получения правильного тетраэдра необходимо построить куб – правильный многогранник, каждая грань которого является квадратом.

В построенном квадрате необходимо взять одну из его вершин, например, вершину A. К этой вершине сходятся три квадратные грани равны между собой как диагонали граней куба, поэтому фигура ABCD является правильным тетраэдром.

Урок «Тэтраэдр»

Добрый день! Мы продолжаем с вами изучать тему: «Параллельность прямых и плоскостей».

Я думаю, уже понятно, что сегодня речь пойдет о многогранниках- поверхностях геометрических тел, составленных из многоугольников.

А именно о тетраэдре.

Проводить изучение многогранников будем по плану:

1. определение тетраэдра

2. элементы тетраэдра

3. развертка тетраэдра

4. изображение на плоскости

1. построим треугольник АBC

2. точка D, не лежащая в плоскости этого треугольника

3. соединяем точку D отрезками с вершинами треугольника ABC. Получим треугольники DAB, DBC и DCA.

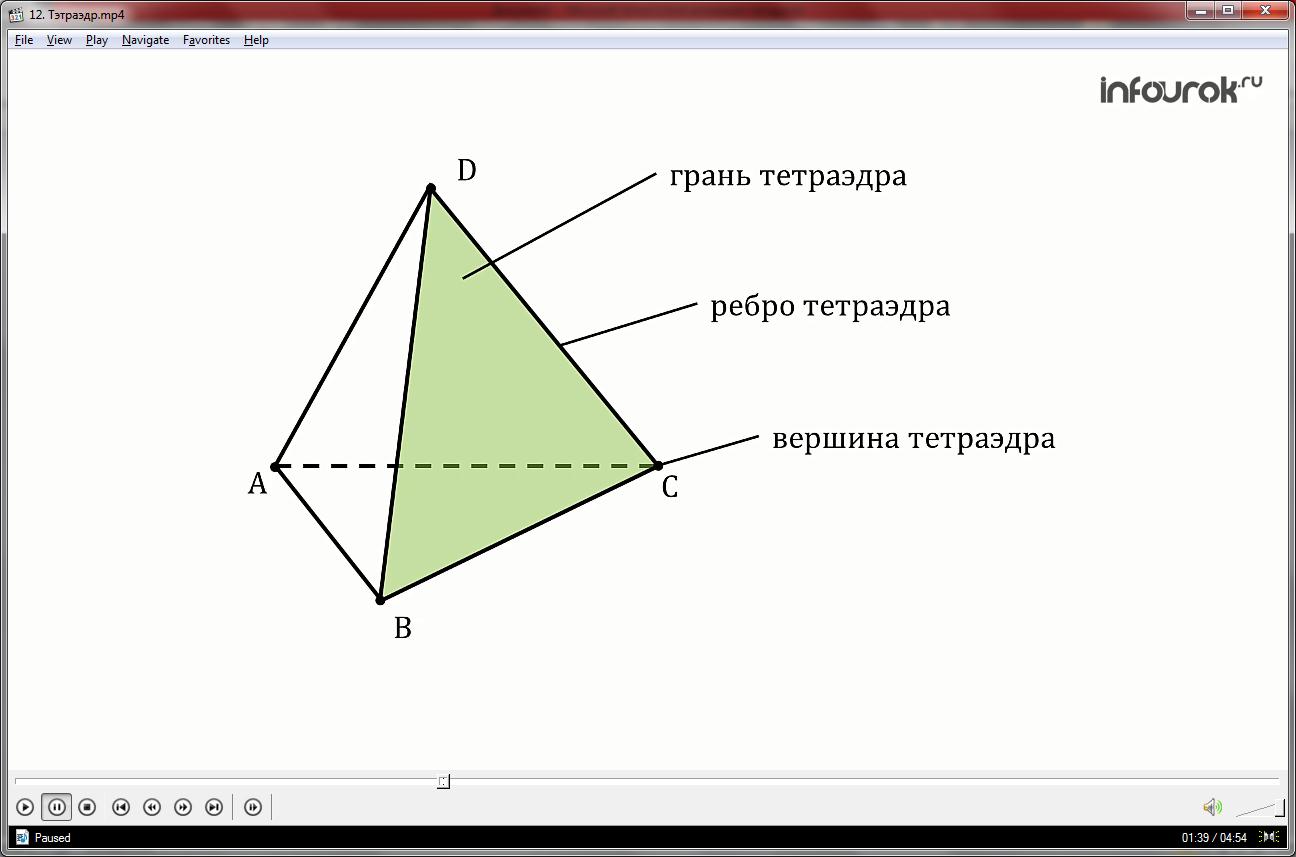
Определение: Поверхность составленная из четырех треугольников АBC, DAB, DBC и DCA называется тетраэдром.

Треугольники, из которых состоит тетраэдр, называются гранями, их стороны ребрами, а вершины – вершинами тетраэдра.

Сколько граней, ребер и вершин имеет тетраэдр?

Тетраэдр имеет четыре грани, шесть ребер и четыре вершины

Два ребра тетраэдра, не имеющие общих вершин, называются противоположными.

На рисунке противоположными являются ребра AD и BC, BD и AC, CD и AB

Иногда выделяют одну из граней тетраэдра и называют ее основанием, а три другие – боковыми гранями.

Для изготовления тетраэдра из бумаги вам потребуется следующая развертка,

ее нужно перенести на плотную бумагу, вырезать, согнуть по пунктирным линиям и склеить.

На плоскости тетраэдр изображается

В виде выпуклого или невыпуклого четырехугольника с диагоналями. При этом штриховыми линиями изображаются невидимые ребра.

На первом рисунке AC- невидимое ребро,

на втором – EK, LK и KF.

Решим несколько типовых задач на тетраэдр:

Найти площадь развертки правильного тетраэдра с ребром 5 см.

Решение. Начертим развертку тетраэдра

(на экране появляется развертка тетраэдра )

Данный тетраэдр состоит из четырех равносторонних треугольников, следовательно, площадь развертки правильного тетраэдра равна площади полной поверхности тетраэдра или площади четырех правильных треугольников.

Площадь правильного треугольника ищем по формуле:

Тогда получаем площадь тетраэдра равна:

Подставим в формулу длину ребра а=5 см,

Ответ: Площадь развертки правильного тетраэдра

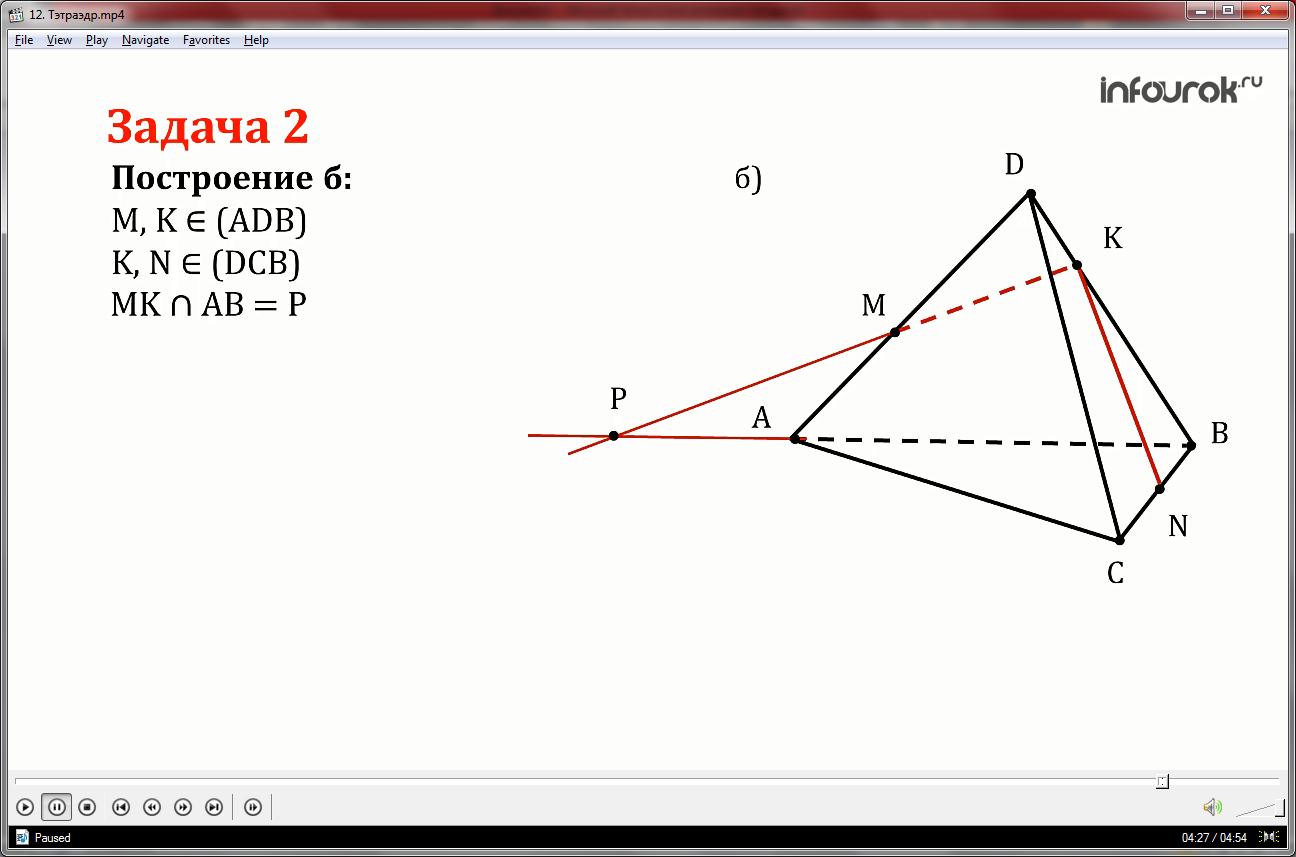
Постройте сечение тетраэдра плоскостью проходящей через точки M, N и K.

а) Действительно, соединим точки M и N (принадлежат грани ADC), точки M и K(принадлежат грани ADB), точки N и K (грани DBC). Сечением тетраэдра является треугольник MKN.

б) Соединим точки M и K (принадлежат грани ADB), точки K и N(принадлежат грани DCB), далее прямые MK и AB продолжить до пересечения и поставить точку P. Прямая PN и точка T лежат в одной плоскости АВС и теперь можно построить пересечение прямой МК с каждой гранью. В результате получается четырехугольник MKNT, который является искомым сечением.

—>

Автор	Инфоурок
Дата добавления	28.10.2014
Раздел	Геометрия
Подраздел	Видеоурок
Просмотров	8607
Номер материала	926

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

Источник

Вы здесь:

Главная
Тетраэдр

Тетраэдр

Древние греки дали многограннику имя по числу граней. «Тетра» означает четыре, «хедра» – означает грань (тетраэдр – четырехгранник).

Поэтому на вопрос – “что такое тетраэдр?”, можно дать следующее определение: “Тетраэдр это геометрическое тело из четырех граней, каждая их которых – правильный треугольник“.

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел.

Тетраэдр имеет следующие характеристики:

Тип грани – правильный треугольник;
Число сторон у грани – 3;
Общее число граней – 4;
Число рёбер, примыкающих к вершине – 3;
Общее число вершин – 4;
Общее число рёбер – 6;

Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны.

Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник.

Отметим, что очень редко, но встречаются геометрические тела, составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани.

Математические характеристики тетраэдра

Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы тетраэдра определяется по формуле:

, где a – длина стороны.

Сфера может быть вписана внутрь тетраэдра.

Радиус вписанной сферы тетраэдра определяется по формуле:

Площадь поверхности тетраэдра

Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой: