Изобретение относится к геодезии и может найти применение при кадастровом учете земельных угодий со сложным рельефом. Сущность: получают массивы цифровых моделей местности аэрокосмическими средствами с высоким пространственным разрешением. Разбивают матрицу ЦММ участка местности на фрагменты с окном |3×3| смежных пикселя. Вычисляют конечные разности первого порядка по координатам х,y относительно центрального пикселя. Находят площадь рельефа численным методом. Технический результат: оперативность, воспроизводимость, повышение точности, достоверности, документальности. 5 ил.
Изобретение относится к геодезии и может найти применение при кадастровом учете земельных угодий со сложным рельефом.
Известен аналитический способ определения площади земельных участков [см. например, “Инженерная геодезия” учебник под редакцией Д.Ш.Михелева, Высшая школа, М., 2000 г., стр.335-337 – аналог]. При аналитическом способе определения площадей применяют формулы геометрии, тригонометрии и аналитической геометрии. При этом оцениваемую площадь разбивают на простейшие геометрические фигуры, преимущественно треугольники (прямоугольники), а площадь участка находят как сумму площадей отдельных фигур (S) вычисляемых: для треугольника по двум сторонам l1, l2 и углу β, заключенному между ними:
![]()
или по формуле Герона:
![]()
где p – полупериметр сторон треугольника равный ![]() .
.
В способе-аналоге площадь участка вычисляют по результатам измерений перечисленных параметров на местности. Результирующая ошибка (стр.337 аналога) определения площади полигона с n вершинами составляет величину:
![]()
где σx,y – среднеквадратическая ошибка определения координат х, у точек вершин полигона при условии, что σx1=σx2=σxn=…=σy1=σy2=…=σyn
Di – расстояние от начала координат до i-ой точки вершины полигона.
Таким образом, к недостаткам способа-аналога следует отнести:
– увеличение результирующей ошибки при усложнении рельефа, т.е. необходимость разбиения полигона на большее число простейших фигур;
– большой объем, трудоемкость наземных измерений, неоперативность работ;
– трудности реализации способа в сложно-пересеченной и горной местности.
В последние годы совершенствуются методы определения площади земельных участков по цифровым моделям местности (ЦММ). Цифровой моделью местности называют совокупность точек местности с известными координатами в трехмерном пространстве х, у, h. Существуют различные методы формирования массивов ЦММ, отличающиеся друг от друга различной точностью и степенью детализации элементов рельефа. Точность ЦММ обычно увязывают с требуемой точностью решения инженерно-геодезических задач. При этом рельеф аппроксимируют криволинейными поверхностями различного порядка.
Наиболее универсальными являются статистические модели местности с разделением на фрагменты, каждый из которых приурочивается к определенной форме рельефа: склон, гора, котловина, лощина, седловина, хребет и в пределах которых назначают свой тип аппроксимирующей функции, т.е. рельеф задается многогранной поверхностью [см. например, Н.П.Булгаков, Е.М.Рывина, Г.А.Федотов “Прикладная геодезия” учебник, Недра, М., 1990 г., §16. Математические модели местности, стр.42-44].
При известной аппроксимирующей функции h(x, у) площадь поверхности рассчитывают аналитически. Ближайшим аналогом является способ аналитического расчета площади криволинейной поверхности [см., например Н.С.Пискунов “Дифференицальное и интегральное исчисления для втузов” учебник, 5-е издание, Наука, М., 1964 г., стр.73-74].
В способе ближайшего аналога площадь (S) криволинейной поверхности, заданной функцией h(x, у) в некоторой области Ф, изменения координат х, у определяют путем вычисления двойного интеграла вида:

Как правило, сложный рельеф местности не может быть выражен простейшими алгебраическими функциями. Поэтому к недостаткам ближайшего аналога следует отнести:
– невозможность непосредственного использования ввиду отсутствия аналитического выражения для функции h(x, у);
– при усложнении аналитического выражения для h(x, у) интеграл от сложного радикала оказывается не берущимся.
Задача, решаемая заявляемым способом, состоит в повышении точности и автоматизации процесса определения площади рельефа, заданного ЦММ, путем разработки специализированной математической программы численного интегрирования для ПЭВМ.
Поставленная задача решается тем, что в способе определения площади рельефа, включающем получение цифровой модели местности (ЦММ) в виде массива дискретных отсчетов зависимости высоты h(x, у) от пространственных координат в области Ф, разбиение матрицы ЦММ на фрагменты, аналитический расчет поверхности как двойной интегральной суммы элементарных фрагментов, дополнительно от начала массива разбивают матрицу на окна |3×3| смежных пикселя, в каждом окне рассчитывают конечные разности по координатам х, у относительно центрального пикселя вида:
![]()
![]()
а площадь рельефа находят численным методом по специализированной математической программе для ПЭВМ как двойную сумму:
![]()
где m, n – число строк, столбцов матрицы ЦММ анализируемого участка;
dx, dy, dh – пространственное разрешение матрицы ЦММ по координатам х, у, h;
a(i, j) – характеристическая функция, равная 1, если (х, у)∈Ф, и равная 0, если (х, у)∉Ф.
Изобретение поясняется чертежами, где:
фиг.1 – визуализированное изображение ЦММ участка;
фиг.2 – последовательность разбиения матрицы ЦММ на окна из |3×3| пикселей;
фиг.3 – криволинейная поверхность фрагмента (окна), кривизна которой задается производными по х, у;
фиг.4 – аппроксимация рельефа мозаикой криволинейных фрагментов;
фиг.5 – функциональная схема устройства, реализующая способ.
Техническая сущность изобретения состоит в следующем. Развитие космических средств наблюдения позволяет в настоящее время получать стереоизображения земной поверхности в видимом диапазоне с разрешением менее 5 м на пиксел. Программные методы обработки стереоизображений [см. например, “Фотограммическая обработка аэроснимков на универсальных стереопарах” в учебнике “Прикладная геодезия”, Н.П.Булгаков, Е.М.Рывкина, Г.А.Федотов, Недра, М., 1990 г., стр.241-247] позволяет формировать цифровые карты местности, широко используемые в военном деле, геодезии, навигации, развитии сотовой связи и др. областях. При наличии ЦММ высокого разрешения представляется возможным решение геодезических задач, в частности вычисление площади рельефа на новом уровне с высокой точностью и документальностью. Цифровая модель местности представляется функцией зависимости высоты h=h(x,y) от пространственных координат х, у. На фиг.1 представлено визуализированное изображение ЦММ обрабатываемого участка. На фиг.2 представлена иллюстрация последовательности разбиения матрицы ЦММ на окна их 4-х смежных пикселей. Каждый пиксел ЦММ характеризуется разрешением по координатам Δx, Δy, Δh, которые считаются известными из технических характеристик средств.
Размер участка определяется числом строк (m) и столбцов (n) матрицы.
Алгоритм вычисления элементарной площади строится на представлении рельефа мозаикой многогранников из фрагментов (окон) |3×3| пикселей. При этом кривизна поверхности фрагмента (окна) определяется значениями производных по х, у, задающими наклон граней многогранника. Процедура представления поверхности окна в виде многогранника иллюстрируется фиг.3, а представление рельефа мозаикой многогранников – фиг.4.
С целью сохранения единообразия формул расчета производных для внутренних и граничных точек области Ф массив дискретных отсчетов расширяют до размеров 0≤i≤n+1, 0≤j≤m+1, поместив в дополнительные фиктивные узлы значения h из соответствующих приграничных узлов:
h(0,j)=h(2,j),h(n+1,j)=h(n-1,j)
h(i,0)=h(i,2),h(i,m+1)=h(i,m-1)
Вычисления осуществляют по специализированной программе для ПЭВМ.



Пример реализации способа.
Заявляемый способ может быть реализован на базе устройства по схеме фиг.5. Функциональная схема устройства фиг.5 содержит орбитальный комплекс наблюдения 1 типа космического аппарата (КА) “Ресурс” с установленной на его борту оптической системой стереосъемки типа MOMS-2Р (ФРГ) с каналами 2, 3 формирования стереоизображения. Съемка запланированных участков местности и включение каналов 2, 3 осуществляет бортовой комплекс управления (БКУ) 4 по командам, передаваемым из центра управления полетом (ЦУП) 5 по радиолинии управления 6. Информацию стереоизображений подстилающей поверхности 7 записывают на бортовой видеомагнитофон 8 и в сеансах видимости КА с наземных пунктов сбрасывают посредством телеметрической системы 9 по автономному каналу связи 10 на наземные пункты приема информации 11, где осуществляется запись массивов информации на видеомагнитофон 12 типа “Арктур”.
Предварительную обработку информации, выделение кадров по служебным признакам и формирование ЦММ осуществляют в Картографическом центре 13 Министерства Природных Ресурсов. Скомпонованные массивы ЦММ по запросам потребителей передаются в Региональные центры кадастрового учета 14, где ведется архив 15 ЦММ региона на базе стримеров, типа FT-120. Программный расчет площади рельефа участков осуществляют на ПЭВМ 16 в стандартном наборе элементов: процессора 17, ОЗУ 18, винчестера 19, дисплея 20, принтера 21, клавиатуры 22. Расчетные значения площадей участков помещают в базу региональных данных с выводом на сайт сети “Интернет” 23.
Программу вычисления площади рельефа записывают на винчестер 19. На электронной карте ЦММ высота (глубина) рельефа обычно квантуется в стандартной шкале от 0 до 255 уровней.
Обрабатываемый участок может иметь произвольную конфигурацию. Для его обработки следует выполнить выделение границы участка, “залив” окрестности белым цветом (255). Предполагается, что на обрабатываемом участке максимально возможная высота 255 не достигается. Если это не так, следует использовать изображение местности, выполненное в другом масштабе глубины. Для вычисления площади поверхности обрабатываемого участка необходимо указать масштаб по горизонтали, вертикали и глубине, то есть указать, чему соответствует в метрах один пиксель по горизонтали (Δх), по вертикали (Δу) и одна единица глубины (Δh).
Пусть область Ф имеет m дискретов по горизонтали (х) и n дискретов по вертикали (у). Массив дискретных отсчетов обозначим h(i,j), где 1≤i≤n, 1≤j≤m, 0≤h(i,j)≤255.
Визуализированное изображение обрабатываемой ЦММ представлено на фиг.1. Один пиксель изображения соответствовал 5 м пространства (Δx=Δy=5 м), а единица глубины составила 7 м. Число строк изображения ЦММ 490, число столбцов 512. Площадь рельефа 1020 га, площадь проекции рельефа на подошву (основание) 630 га.
В соответствии с теоремой отсчетов Котельникова-Шеннона для точного восстановления рельефа по его дискретным отсчетам интервал дискретизации функции сигнала должен соответствовать: Δρ≤1/2Fmax, где
Fmax – максимальная пространственная частота рельефа ![]() ; Δρ – интервал дискретизации
; Δρ – интервал дискретизации ![]()
Таким образом, точность заявляемого способа определяется соотношением между “шероховатостью” рельефа и дискретностью отсчетов ЦММ.
При использовании аэрокосмических средств получения ЦММ высокого пространственного разрешения преимущества заявляемого способа перед аналогами по гамме показателей (как оперативность, достоверность, воспроизводимость, точность, документальность) очевидны.
Способ определения площади рельефа, включающий получение цифровой модели местности (ЦММ) в виде массива дискретных отсчетов зависимости высоты h(x,y) от пространственных координат в области Ф, разбиение матрицы ЦММ на фрагменты, аналитический расчет поверхности как двойной интегральной суммы элементарных фрагментов, отличающийся тем, что цифровую модель местности определяют по записанной информации стереоизображений подстилающей поверхности, полученных путем съемки заданных участков орбитальным комплексом наблюдения с помощью оптической системы, по программным расчетам последовательно от начала массива разбивают матрицу на окна из |3×3| смежных пикселя, в каждом окне рассчитывают конечные разности по координатам х,y относительно центрального пикселя вида:
![]()
![]()
а площадь рельефа находят численным методом по формуле:
![]()
где m, n – число строк, столбцов матрицы ЦММ анализируемого участка,
dх, dy, dh – пространственное разрешение матрицы ЦММ по координатам х, y, h,
a(i,j) – характеристическая функция, равная 1, если (х,y)![]() Ф, и равная 0, если (х,y)∉Ф.
Ф, и равная 0, если (х,y)∉Ф.
Время от времени возникает задача рассчитать площадь поверхности с учетом ее наклона, т.е. того, что эта поверхность находится в трехмерном пространстве. Эта статья рассматривает пример того, как эту задачу можно решить в GRASS GIS.
Для примера возьмем набор geosample (http://gis-lab.info/qa/geosample.html). Данный набор содержит растр высот (слой relief) и векторную карту охраняемых природных территорий (слой oopt). Требуется посчитать площади каждой из охраняемых территорий как с учетом рельефа, так и без этого.
[править] Перепроецирование
Поскольку набор geosample содержит данные в географической системе координат (широта/долгота), а измерения требуется произвести в метрической системе координат, то их предварительно нужно перепроецировать, например в равноплощадную проекцию Альберса. Для этого создадим еще один набор geosample_sib_aea в новой проекции со следующими параметрами:
north: 6184472.19979012 south: 5008416.36981374 west: 16373043.44324575 east: 17599228.40562719 nsres: 659.6 ewres: 659.6
Заходим в этот набор и перепроецируем растровые данные (здесь и ниже галочка “>” означает приглашение командной строки GRASS, после нее вводится сама команда, в данном случае команда “r.proj loc=geosample in=relief out=relief”):
> r.proj loc=geosample in=relief out=relief
Аналогично перепроецируем векторные данные:
> v.proj loc=geosample in=oopt out=oopt
Посмотрим поближе на исходные данные (слой relief):
> r.info relief +----------------------------------------------------------------------------+ | Layer: relief Date: Wed Aug 17 18:08:10 2011 | | Mapset: PERMANENT Login of Creator: dima | | Location: geosample_sib_aea | | DataBase: /home/dima/laboro/GRASSDATA | | Title: ( relief ) | | Timestamp: none | |----------------------------------------------------------------------------| | | | Type of Map: raster Number of Categories: 4197 | | Data Type: CELL | | Rows: 1782 | | Columns: 1859 | | Total Cells: 3312738 | | Projection: Albers Equal Area | | N: 6184472.19979012 S: 5009075.96366118 Res: 659.59384743 | | E: 17599228.40562719 W: 16373043.44324575 Res: 659.5938474 | | Range of data: min = 20 max = 4197 | | | | Data Description: | | generated by r.proj | | | | Comments: | | r.proj input="relief" location="geosample" output="relief" method="n | | earest" | | | +----------------------------------------------------------------------------+
Аналогично по слою oopt:
> v.info oopt +----------------------------------------------------------------------------+ | Layer: oopt | | Mapset: PERMANENT | | Location: geosample_sib_aea | | Database: /home/dima/laboro/GRASSDATA | | Title: | | Map scale: 1:1 | | Map format: native | | Name of creator: dima | | Organization: | | Source date: Wed Aug 17 16:36:58 2011 | |----------------------------------------------------------------------------| | Type of Map: vector (level: 2) | | | | Number of points: 0 Number of areas: 8 | | Number of lines: 0 Number of islands: 8 | | Number of boundaries: 8 Number of faces: 0 | | Number of centroids: 8 Number of kernels: 0 | | | | Map is 3D: No | | Number of dblinks: 1 | | | | Projection: Albers Equal Area | | N: 5929488.79257984 S: 5114805.91166458 | | E: 17470617.17073559 W: 16788858.38019306 | | | | Digitization threshold: 0 | | Comments: | | | +----------------------------------------------------------------------------+
[править] Расчет площадей
GRASS содержит модуль r.surf.area (http://grass.osgeo.org/gdp/html_grass64/r.surf.area.html), который производит требуемые расчеты. Рассчитаем общую площадь всей территории охвата слоя relief с использованием данного модуля:
> r.surf.area relief Null value area ignored in calculation 5.439092e+11 Plan area used in calculation: 1.440478e+12 Surface Area Calculation(low, high, avg): 9.009841e+11 9.024818e+11 9.017329e+11 Current Region plan area: 1.442062e+12 Estimated Region Surface Area: 9.027246e+11 Done.
Остановимся подробнее на результатах расчета:
- Null value area ignored in calculation: площадь ячеек растра, которые не участвовали в расчетах (были замаскированы).
- Plan area used in calculation: площадь всего растра как площадь проекции растра на горизонтальную плоскость.
- Surface Area Calculation(low, high, avg): площадь растра с учетом рельефа. Рассчитывается путем построения треугольников, вершины которых находятся в центре ячеек растра. Поскольку для соседних ячеек можно построить несколько вариантов триангуляции (см. пример на рисунке), то и результаты расчета площадей могут различаться. Поэтому алгоритм сохраняет минимальное, максимальное и среднее ((минимальная + максимальная)/2) значение расчетной площади для каждой пары треугольников.
- Current Region plan area: площадь текущей области (без учета рельефа).
- Estimated Region Surface Area: итоговая расчетная площадь территории.

![]()
На рисунке показаны два различных варианта построения треугольников при расчете площади поверхности (синими точками обозначены узлы решетки растра — 9 ячеек)

![]()
На рисунке показаны два различных варианта построения треугольников при расчете площади поверхности (ячейки растра представлены вертикальными столбиками — 4 ячейки)
Таким образом, получаем, что величина 9.027246e+11 — искомая площадь территории с учетом рельефа, 1.440478e+12 — общая площадь без учета рельефа (если необходимо произвести сравнение площадей с учетом и без учета рельефа, то из общей площади 1.440478e+12 сначала нужно вычесть число 5.439092e+11 — площадь пустых ячеек, которые в расчетах не участвовали).
Нужно заметить, что результаты расчетов модуля зависят от текущего разрешения (что вполне естественно, т.к. результат и должен зависеть от точности исходных данных).
Посмотрим на текущее разрешение:
> g.region -p projection: 99 (Albers Equal Area) zone: 0 datum: ** unknown (default: WGS84) ** ellipsoid: krassovsky north: 6184472.19979012 south: 5008416.36981374 west: 16373043.44324575 east: 17599228.40562719 nsres: 659.59384743 ewres: 659.59384743 rows: 1783 cols: 1859 cells: 3314597
Огрубим разрешение:
> g.region res=6596 -p projection: 99 (Albers Equal Area) zone: 0 datum: ** unknown (default: WGS84) ** ellipsoid: krassovsky north: 6184472.19979012 south: 5008416.36981374 west: 16373043.44324575 east: 17599228.40562719 nsres: 6607.05522459 ewres: 6592.39227087 rows: 178 cols: 186 cells: 33108
И рассчитаем площади с новым разрешением:
> r.surf.area relief Null value area ignored in calculation 5.440617e+11 Plan area used in calculation: 1.426251e+12 Surface Area Calculation(low, high, avg): 8.825813e+11 8.827467e+11 8.826640e+11 Current Region plan area: 1.442062e+12 Estimated Region Surface Area: 8.924489e+11
Как видим, результаты разнятся, и это нужно учитывать при работе.
Вернем разрешение к исходному разрешению растра:
> g.region rast=relief -p projection: 99 (Albers Equal Area) zone: 0 datum: ** unknown (default: WGS84) ** ellipsoid: krassovsky north: 6184472.19979012 south: 5009075.96366118 west: 16373043.44324575 east: 17599228.40562719 nsres: 659.59384743 ewres: 659.59384743 rows: 1782 cols: 1859 cells: 3312738
[править] Расчет площадей по отдельным участкам
Однако, наша задача несколько иная: нужно расчитать площади по каждому из заповедников в отдельности. Для того, чтобы это сделать, необходимо следующее:
- Извлечь из карты oopt интересующий нас полигон.
- Создать маску из этого полигона, чтобы команда “r.surf.area relief” производила расчеты только в замаскированной области
- Вызов команды r.surf.area relief и сохранение результата
Реализация:
Посмотрим содержимое таблицы атрибутов карты oopt:
> v.db.select oopt cat|NAME_PRT_R|NAME_R|TYPE 1|Катунский|Катунский|Заповедник 2|Кузнецкий Алатау|Кузнецкий Алатау|Заповедник 3|Участок "Ханхаринский"|Тигирекский|Заповедник 4|Участок "Белорецкий"|Тигирекский|Заповедник 5|Участок "Тигирекский"|Тигирекский|Заповедник 6|Алтайский|Алтайский|Заповедник 7|Шорский|Шорский|Национальный 8|Кирзинский|Кирзинский|Заказник
Создадим из векторной карты oopt растровую:
> v.to.rast in=oopt out=oopt use=attr col=cat label=NAME_PRT_R
Посмотрим, что из этого получилось, заодно рассчитаем статистику по площадям:
> r.report oopt un=k 100% +-----------------------------------------------------------------------------+ | RASTER MAP CATEGORY REPORT | |LOCATION: geosample_sib_aea Wed Aug 17 18:38:50 2011| |-----------------------------------------------------------------------------| | north: 6184472.19979012 east: 17599228.40562719 | |REGION south: 5009075.96366118 west: 16373043.44324575 | | res: 659.59384743 res: 659.59384743 | |-----------------------------------------------------------------------------| |MASK:none | |-----------------------------------------------------------------------------| |MAP: Labels (oopt in PERMANENT) | |-----------------------------------------------------------------------------| | Category Information | square | |#|description |kilometers| |-----------------------------------------------------------------------------| |1|Катунский . . . . . . . . . . . . . . . . . . . . . . . . . . . | 1501| |2|Кузнецкий Алатау. . . . . . . . . . . . . . . . . . . . . . . . | 3993| |3|Участок "Ханхаринский". . . . . . . . . . . . . . . . . . . . . | 4| |4|Участок "Белорецкий". . . . . . . . . . . . . . . . . . . . . . | 388| |5|Участок "Тигирекский". . . . . . . . . . . . . . . . . . . . . .| 17| |6|Алтайский . . . . . . . . . . . . . . . . . . . . . . . . . . . | 8770| |7|Шорский . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 4201| |8|Кирзинский . . . . . . . . . . . . . . . . . . . . . . . . . . .| 1196| |*|no data. . . . . . . . . . . . . . . . . . . . . . . . . . . . .| 1,421,182| |-----------------------------------------------------------------------------| |TOTAL | 1,441,253| +-----------------------------------------------------------------------------+
Создадим маску, соответствующую участу “Катунский” (категория 1):
Расчитаем площадь для этого участка:
> r.surf.area relief Null value area ignored in calculation 1.439753e+12 Plan area used in calculation: 1.439670e+12 Surface Area Calculation(low, high, avg): 1.447004e+09 1.467648e+09 1.457326e+09 Current Region plan area: 1.441253e+12 Estimated Region Surface Area: 1.458929e+09 Done.
Таким же образом можно получить информацию и по остальным участкам.
Эту процедуру легко автоматизировать, сохранив данные расчетов в файл, например, area.txt:
> for id in `seq 8` do r.mask -r r.mask oopt maskcat=$id r.category oopt cat=$id >> area.txt r.surf.area relief >> area.txt done
Начальные строки файла area.txt представлены ниже:
1 Катунский Null value area ignored in calculation 1.439753e+12 Plan area used in calculation: 1.439670e+12 Surface Area Calculation(low, high, avg): 1.447004e+09 1.467648e+09 1.457326e+09 Current Region plan area: 1.441253e+12 Estimated Region Surface Area: 1.458929e+09 Done. 2 Кузнецкий Алатау Null value area ignored in calculation 1.437260e+12 Plan area used in calculation: 1.439670e+12 Surface Area Calculation(low, high, avg): 3.870987e+09 3.888315e+09 3.879651e+09 Current Region plan area: 1.441253e+12 Estimated Region Surface Area: 3.883918e+09 Done.
Скачать с Depositfiles

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ
ПО КУРСУ «ГЕОДЕЗИЯ ч.1»
7. И3МЕРЕНИЕ ПЛОЩАДЕЙ ПО ПЛАНУ ИЛИ КАРТЕ
Для решения ряда инженерных задач требуется определить по плану или картеплощади различных участков местности. Определение площадей может бытьпроизведено графическим. аналитическим и механическим способами.
7.1. Графический способ определения площади
Графический способ служит для определения по плану или карте площадейнебольших участков (до 10-15 см2) и применяется в двух вариантах: а)с разбивкой намеряемого участка на геометрические фигуры; б) о помощью палеток.
В первом варианте площадь участка разбивают на простейшие гео-метрическиефигуры: треугольники, прямоугольники, трапеции (рис. 19, а), измеряютсоответствующие элементы этих фигур (длины оснований и высоты) и по геометрическимформулам вычисляют площади этих фигур. Площадь всего участка определяется каксумма площадей отдельных фигур. Разбивку участка на фигуры следует выполнять такимобразом, чтобы фигуры были возможно больших размеров, а их стороны повозможности ближе совпадали о контуром участка.
Для контроля площадь участка разбивают на другие геометрические фигуры иповторно определяют площадь. Относительное расхождение в результатах двукратныхопределений общей площади участке не должно превышать 1: 200.
Для малых участков (2-З см2) с резко выраженными криволинейными границамиопределение площади целесообразно производить с помощью квадратной палетки (рис. І9, б). Палетку можно изготовитьна кальке, расчертив ее сеткой квадратов со сторонами 2-5 мм. Зная длину сторони масштаб плана, можно вычислить площадь квадрата палетки IKB.
Для определения площади участка палатку произвольно накладывают на план и подсчитывают число полных квадратов N1 , расположенных внутри контура участка. Затем оценивают на глаз (в десятых долях) каждый неполный квадрат и находят суммарное число N2 для всех неполных квадратов на границах контура. Тогда общая площадь измеряемого участка
S=sKB *(N1+N2).
Для контроля палатку разворачивают примерно на 45 а и производят повторное определение площади. Относительная погрешность определения площади квадратной палеткой составляет 1 : 50 - 1 : 100. При определении площадей несколько более крупных участков (до 10 см2 ) можно использовать линейную палетку (рис. 19, в), которую можно изготовить на кальке, проводя через равные промежутки (2-5 мм) ряд параллельных линий.
Палетка накладывается на данный участок таким образом, чтобы крайние точки участка (точки m и n на рис. 19, в) разместились посредине между параллельными линиями палетки. Затем измеряют с помощью циркуля-измерители и масштабной линейки длины линий l1 , l2 ….., ln , являющиеся средними линиями трапеции, на которые оказывается разбитой с помощью палетки площадь данного участка.
Тогда площадь участка
S=a(l1+l2+……+ln ),
где a - шаг линейной палетки, т.е. расстояние между параллельными линиями.
Для контроля палетку расчерчивают на 60-90о относительно первоначального положении и повторно определяют площадь участка. Относительная погрешность определения площади линейной палаткой зависит от ее шага и составляет 1 : 50 - 1 : 100
7.2. Аналитический способ определения площади
Если по контуру площади измеряемого участка набрать достаточно точек, чтобы с требуемой точностью аппроксимировать данный участок многоугольником, образованным этими точками (рис. 19, а), а затем измерить на карте координаты х и у всех точек, то площадь участка можно определить аналитическим способом.

Для многоугольника о числом вершин n при их оцифровка по ходу часовой стрелки площадь будет определяться по формулам

Для контроля вычисления производит по обеим формулам. Точность аналитического способа зависит от густоты набора точек по контуру измеряемого участка. При значительном числе точек целесообразно вычисления проводить с использованием компьютеров или микрокалькуляторов=
7.3. Механический способ определения площади с помощью планиметра
Планиметром называется механический прибор для измерения площади. В инженерно-геодезической практике с помощью планиметра по планам или картам измеряют площади достаточно больших участков. Из многочисленных конструкций планиметров наибольшее распространение получили полярные планиметры.
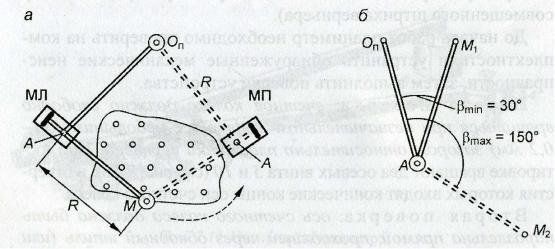
Полярный планиметр (рис. 20) состоит из двух рычагов - полюсного 1 и обводного 4. В нижней части груза 2, закрепленного на одном из концов полюсного рычага, имеется игла - полюс планиметра. На втором конце полюсного рычага находится штифт с шарообразной головкой, которая вставляется в специальное гнездо в каретке 5 обводного рычага. На конце обводного рычага имеется линза 3, на которой нанесена окружность с обводной точкой в центре.
Каретка 5 имеет счетный механизм, состоящий из счетчика 6 целых оборотов счетного колеса и самого счетного колеса 7. Для отсчетов по очетному колесу имеется специальное устройство - верньер 8. При ообводе контура участка обводной линзы 3 ободок счетного колеса и ролик 9 катится или скользит по бумаге, образуя вместе с обводной точкой три опорные точки планиметра. В современных планиметрах каретка со счетным механизмом может перемещаться вдоль обводного рычага, изменяя тем самым его длину, и фиксироваться я новом положении.
Окружность счетного колеса разделена на 100 частей, каждый десятый штрих оцифрован. Отсчет по планиметру состоит из четырех цифр: первая цифра - ближайшая к указателю меньшая цифра счетчика оборотов (тысячи делении планиметра), вторая и третья цифры – сотни и десятки делении на счетном колесе, предшествующие нулевому штриху верньера; четвертая цифра - номер штриха верньера, совпадающего с ближайшим штрихом счетного колеса (единицы делении).
Перед измерением площади участке планиметр устанавливают на карте так, чтобы его полюс располагался вне измеряемого участка, в полюсный и обводной рычаги образовывали примерно прямой угол.
При этом место закрепления полюса выбирают с расчетом, чтобы во время обвода всей фигуры угол между обводным и полюсными рычагами был не менее 30° и не более 150 °.
Совместив обводную точку планиметра с некоторой исходной точкой контура участка, снимают по счетному механизму начальный отсчет no и плавно обводят весь контур по ходу часовой стрелки. Вернувшись в исходную точку, берут конечный отсчет n . Разность отсчетов (n -no ) выражает величину площади фигуры в делениях планиметра. Тогда площадь измеряемого участка

Где µ-цена деления планиметра, т.е. площадь, соответствующая одному делению планиметра.
Для контроля и повышения точности результатов измерений площадь участка измеряют при двух положениях полюса планиметра относительно счетного механизма: "полюс лево" и "полюс право".
Перед измерением площадей необходимо определить цену деления планиметра µ . Для этого выбирают фигуру, площадь которой Ѕо известна заранее (например, один или несколько квадратов координатной сетки). С целью получения более высокой точности данную фигуру обводят по контуру 4 раза: 2 раза при положении "полюс право" и 2 раза при положении "полюс лево". При каждом обводе берут начальный и конечный отсчеты и вычисляют их разность ( ni-noi). Расхождения между значениями разностей при "полюсе право" и "полюсе лево" не должны превышать 2 делении при площади фигуры до 200 делении, 3 делений - при площади фигуры от 200 до 2000 делении и 4 делений - при площади фигуры свыше 2000 делении планиметра.
Если расхождения не превышают допустимых, то рассчитывают среднюю разность отсчетов (n-no)ср и вычислят цену деления планиметра по формуле
 / (n-no)ср
/ (n-no)ср Цену деления вычисляют с точностью до 3-4 значащих цифр.
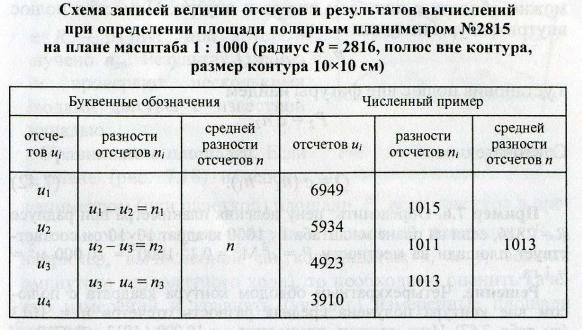
В таблице (с. 39) приведен пример записи результатов измерений цены деления планиметра и определения площади участка на карте.
Точность определения площадей полярным планиметром зависит от размеров измеряемых участков. Чем меньше площадь участка, тем больше относительная погрешность ее определения. Планиметром рекомендуется измерять площади участков на плане (карта) не менее 10-12 см2. При благоприятных условиях измерений относительная погрешность определения площадей с помощью планиметра составляет примерно 1 : 400.
8. ОПИСАНИЕ КАРТЫ
При проведении инженерно-геодезических изысканий составление технической документации требует от исполнителя хорошего знания условных знаков и основных закономерностей размещений природных объектов (например, взаимной согласованности рельефа, гидрографии, растительности, населенных пунктов, дорожной сети и т.д.). Часто при этом возникает необходимость в описании тех или иных участков карты
Для выполнения описания участка карты рекомендуется использовать следующую схему.
І. Название (номенклатура) карты.
2. Выходные данные:
2.1. Где , когда и кем составлена и издана карта.
2.2. По каким картографическим материалам изготовлена.
3. Математические элементы карты:
3.1. Масштаб карты.
3.2. Долготы и широты рамок карты.
3.3. Километровая сетка, частота ее линий и их оцифровка.
3.4. Расположение на карте описываемого участка.
3.5. Геодезическая основа на описываемом участие карты (виды опорных знаков, их количество).
4. Физико-географические элементы: гидрографии (моря, реки, озера, каналы, оросительные и осушительные системы); рельеф, его характер, господствующие высоты и самые низкие места, их отметки; растительный покров.
5. Социально-экономические элементы: населенные пункты, пути сообщения, средства связи, промышленность, сельское и лесное хозяйство, элементы культуры.
В качестве примера приводится следующее описание одной из участков карты масштаба 1 : 25 000.
І. Карта У-34-37-В-в (Снов).
2. Выходные данные:
2.1. Карта подготовлена к изданию в 1981 г. ГУГК и отпечатана в 1982 г. Снимал Иванов А.П.
2.2. Карта составлена по материалам аэрофототопографической съемки 1980 г.
3. Математические элементы карты:
3.1. Масштаб карты 1 : 25 000.
3.2. Лист карты ограничен по долготе меридианами 18о 00’ 00’’ (на западе) и І8°07’'З0’’ (на востоке) и по широте – параллелями 54o 40’ 00’’ (на юге) и 54°45’00’’ (на севере).
3.3. На карте нанесена километровая сетка прямоугольных координат (через 1 км). Квадраты сетки имеют на карте размеры сторон 40 мм (в масштабе карты 1 см соответствует 250 м на местности). На листе карты нанесены 9 горизонтальных линий километровой сетки (от х = 6065 км на юге до х= 6073 км на севере) и 8 вертикальных линий сетки (от у = 4307 км на западе до у = 4314 км на востоке).
3.4. Описываемый участок карты занимает четыре квадрата километровой сетки (от х1 = 6068 км до х2 = 6070 км и от у1 =4312 км до у2 = 4314 км) к востоку от центрального участка карты.
Определение площади участка планиметром
Положение полюса
Номер
Отсчеты
Разность
r=n- n0
Средняя
rcp
Относительная ошибка
(rпп-rпл)/ rcp
Цена деления
µ=so/rcp
Площадь контура
S=µ* rcp
n0
n
1. Определение цены деления планиметра (So=4км2=400га)
ПП
1
2
0112
0243
6414
6549
6302
6306
6304
1:3152 0,06344 га/дел.
ПЛ
1
2
0357
0481
6662
6788
6305
6307
6306
2. Определение площади участка
ПП
ПЛ
1
2
0068
0106
0912
0952
844
846
945
1:472 0,06344 га/дел. 59,95га
3.5. На описываемом участке карты имеется один пункт геодезической сети, установленный на горе Михалинской.
4. Физико-географические элементы.
В северо-восточном углу описываемого участка протекает река Соть шириной свыше 250 м. Направление ее течения с северо-запада на юго-восток, скорость течения 0,1 м/с. На западном берегу реки установлен постоянный знак береговой речной сигнализации. Берега реки заболоченные, покрытые луговой растительностью. Кроме того, на восточном берегу реки имеются отдельные кустарники. В реку Соть на описываемом участке впадают два ручья, протекающие по дну оврагов, выходящих к реке.
Кроме указанных оврагов, к раке выходит еще один овраг и в юго-западной части участка находятся два оврага, покрытые сплошной растительностью. Рельеф местности холмистый, с перепадами высот свыше 100 м. Господствующими высотами являются гора Большая Михалинская с отметкой вершины 213,8 м в западной части участка и гора Михалинская с отметкой вершины 212,8 м в южной части участка. От этих высот рельеф поднимается к реке (с отметкой уреза воды около 108,2 м). На северном участке берег обрывистый (с высотой обрыва до 10 м). Наблюдается также некоторое понижение рельефа от указанных высот к юго-западу.
В южной части участка находится лес Северный, занимающий около 0,25 км2 и расположенный в седловине между указанными высотами и к востоку от седловины. Преобладающая порода деревьев в лесу- сосна, высота деревьев в среднем около 20 м, средняя толщина деревьев 0,20 м, расстояние между деревьями 6 м. В южной части участка к лесу Северном примыкает участок редколесья и вырубленного леса. На западном склоне горы Михалинской имеется отдельно стоящее дерево, имеющее значение ориентира.
5. Социально-экономические элементы.
На описываемом участке нет населенных пунктов, но сразу за его пределами на юго-западе имеется населенный пункт Михалино, насчитывающий 33 дома. На площадь участка попадают частично сады этого населенного пункта. На участке имеется три грунтовых (проселочных) дороги. Одна из них проходит с запада на юго-запад участка, другая идет с юго-запада на север и переходит на самом краю участка в полевую дорогу. В точке этого перехода дорога разветвляется и с севера на юго-восток идет третья грунтовая (просе-
лочная) дорога. От этой третьей дороги на юго-востоке отходит в южном направлении еще одна половая дорога. Других социально-экономических элементов на данном участке карты нет.
9. ОФОРМЛЕНИЕ ОТЧЕТА
Отчет о лабораторных работах по топографической карте состоит из пояснительной записка и графических документов.
Пояснительная записка содержит списание выполненных лабораторных работ, объяснение полученных результатов. Пояснительнаязаписка оформляется на отдельных листах писчей бумаги (стандартного формата 210 х 297 мм). Каждая лабораторная работа должна иметь наименование и сведения о карте, по которой она выполнялась, и дату выполнения работы. Пояснительная записка должна иметь титульный лист, на котором необходимо указать наименование факультета, группы, фамилию студента, выполнившего работы, фамилию преподавателя, выдавшего задание и проверяющего работу, дату выполнения работы.
Графические документы представляют собой копию и топографический профиль. Эти документы вкладываются в пояснительную записку. Копия карты вычерчивается тушью на кальке, при этом копирует зарамочное оформление карты (оформительскую и градусную рамки, подписи), километровую сетку. На копию карты на кальке делают также выкопировки тех участков карты, которые необходимы для иллюстрации решения той или иной задачи, например, при проектировании линии заданного уклона, при определении границ водосборной площади, при описании участка карты. Топографический профиль вычерчивают тушью на миллиметровой бумаге, причем линия профиля должна быть обязательно показана на копии карты и должны быть скопированы на ней горизонтали, непосредственно прилегающие (по 1 см в каждую сторону) к линии профиля.
Другие графические схемы и рисунки, иллюстрирующие решение задач по топокарте, допускается помещать в текст пояснительной записки. Все чертежи должны быть выполнены аккуратно, без помарок, с соблюдением размеров, условных знаков и шрифтов. Страницы пояснительной записки должны быть пронумерованы, а сама записка должна иметь оглавление.
Отсчет сдается на проверку преподавателю, после чего на занятии он защищается студентом.
Статьи по теме:
Скачать с Depositfiles

Как измерили площадь земли если рельеф не ровный?
Ученик
(66),
закрыт
7 лет назад
Дополнен 7 лет назад
Почему не меряют каждый метр земли с учетом уклона и не сложат для получения площади земли?
Дополнен 7 лет назад
Получается площадь земли еще не определили ?
Mikhail Levin
Искусственный Интеллект
(614573)
7 лет назад
в геодезии считаю площадь горизонтальной проекции.
да и та зависит от выбранной картографической проекции. Например, в принятой в мире WGS-84 (и ее клонах в других странах) площадь получается немного меньше, чем в наших СК-42, 63 или 95
Николай Василенко
Ученик
(148)
7 лет назад
С помощью интегральных уравнений. Но с учетом неровностей рельефа площадь поверхности будет зависить от выбора фрактальной размерности, и соответствено результат может быть от площади шара до безконечности в зависимости от длинны “измерительного шеста”
Алексей
Мудрец
(19278)
7 лет назад
Нет никакого смысла считать площади точно: чем больше мы уточняем и чем больше неровностей рассматриваем, тем больше площадь. Например, если мы уточняем с точностью до песчинок, то площадь плоской поверхности метр на метр где-то в 2 раза меньше чем площадь метр на метр, засыпанная песком. Если будем уточнять площадь с точностью, бóльшей, чем размер песчинок, то площадь возрастёт многократно, поскольку поверхностью станет суммарная поверхность всех песчинок. Это справедливо и для бóльших и для меньших неровностей. Если где-то стоит дом, то нужно добавлять площадь поверхности параллелепипеда без нижней грани. А если смотреть ещё точнее, с точностью до того же метра, то добавляются ещё и внутренние площади помещений.. Полагаю, изменчивость морских волн, в т. ч. волн с размерами более 1 метра, ежесекундно изменяет площадь поверхности на процентов эдак 10-20 вверх-вниз, если не больше..
Точность, с которой мы будем считать, будет чистой условностью, т. е. результат не будет иметь практического смысла.
Определение площадей. Геометрические, аналитический
имеханический способы
Внастоящее время площади земельных угодий и инженерных сооружений вычисляют при помощи компьютеров по исходным данным, полученным в результате измерений на местности, по координатам границ объекта, по данным фотографирования местности и др. Но инженер-геодезист должен знать сущность определения площадей объектов традиционными способами, поскольку их геометрия и математическая основа используется в компьютерных программах и нередки случаи, когда приходится определять площади объектов без применения компьютера. К традиционным относятся способы определения площадей: геометрические, аналитические, механические.
15.1.Геометрические способы определения площади
К геометрическим способам определения площади относятся графические (по чертежам местности) и аналитические (расчетные по координатам контура территории).
Графические способы определения площади применяются для небольших участков. На местности (рис. 15.1, а) сложный контур АВСDЕК разделяют на простые геометрические фигуры, вершины которых обозначают вехами. В трапеции АВЕК измеряют основания а и b, высоту h, а в треугольниках ВСD и ВDЕ измеряют основания а1 и а, высоты h1 и h. Площадь участка Р = Р1 + Р2 + Р3, где Р1 = h (а
+ b)/2; Р2 = а1 h1 /2; Р3 = а h2 /2.
Если треугольнике (рис. 15.1, б) измерить две стороны и угол β между ними, то
Р = 0,5ас sin β.
Площадь определяется рассмотренными способами с относительной погреш-
ностью 1 / 1000 – 1/5000.
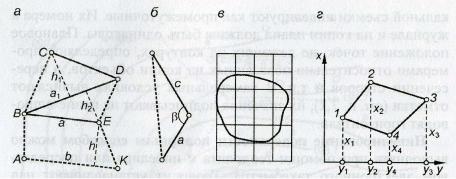
Рис. 15.1. Геометрические способы определения площадей:
а, б – измерением геометрических фигур; в – с помощью палетки; г – по координатам
Аналогичные способы можно применить для графического определения площади по плану масштаба 1 : М, но с относительной погрешностью 1/50 – 1/1000, зависящей от масштаба и точности плана. С помощью карандаша и линейки контур АВСDЕК (см. рис. 15.1, а) разграфляют на плане на простые фигуры, а их площади в нашем примере будут вычисляться по формулам, приведенным выше, или по формулам Р1 = М2 h (а + b)/2; Р2 = М2 а1 h1 /2; Р3 = М2 а h2 /2. Линейные величины а, b и h определяются по плану с погрешностями до 0,5 мм за счет неточностей изображения границ общего контура.
Площадь по плану или карте можно определить при помощи палетки, представляющей прозрачный лист пластика, на который нанесена сетка равных по площади фигур, например квадратов со стороной от 2 до 10 мм (рис. 15.1, в). Техника определения площади палетками рассмотрена в п. 15.4.
15.2. Аналитический способ определения площади
Аналитические способы определения площади применяют для замкнутых плоских многоугольников, в которых известны координаты х и у всех вершин (к таким многоугольникам относятся граница населенного пункта, промышленного, сельскохозяйственного или горно-добывающего предприятия, контур лесного массива, озера, болота и т.д.).
Площадь замкнутого многоугольника вычисляют по различным формулам ана-
|
литической геометрии, наиболее распространены следующие: |
||
|
n |
n |
|
|
2Р = ∑ х i (уi+1 – уi-1); |
2Р = ∑ у i (хi-1 – хi+1); i = 1, 2, …, n, |
(15.2) |
|
i |
i |
т.е. удвоенная площадь многоугольника равна сумме произведений каждой абсциссы на разность ординат передней и задней по ходу точек, а также сумме произведений каждой ординаты на разность абсцисс задней и передней по ходу точек. Например, для многоугольника 1-2-3-4 (рис. 15.1. г)
2Р = х1 (у2 – у4) + х2 (у3 – у1) + х3 (у4 – у2) + х4 (у1 – у3);
. (15.3)
2Р = у1 (х4 – х2) + у2 (х1 – х3) + у3 (х2 – х4) + у4 (х3 – х1);
Площадь вычисляют отдельно по каждой формуле (15.3) с промежуточным контролем разностей координат на условие
|
n |
n |
|
|
∑(уi+1 – уi-1) = 0; |
∑(хi-1 – хi+1) = 0, i = 1, 2, …, n. |
(15.4) |
|
i |
i |
Точность расчетов по формулам (15.4) определяется погрешностями координат. Например, если координаты вершин многоугольника получены теодолитным ходом, то площадь участка получается с относительной погрешностью 1/500 – 1/2000. В случае неверно записанного значения хотя бы одной из координат хi или уi получается ошибочное значение площади при полном совпадении результатов расчетов по формулам (15.3) и (15.4). Такую ошибку можно обнаружить, например, по чрезмерному расхождению между площадью многоугольника и суммой площадей контуров внутри него, нанесенных на план и измеренных планиметром.
15.3. Определение площади полярным планиметром
Полярный планиметр – это механическое устройство для определения площади фигур на планах и картах, а также на других чертежах. На полюсном рычаге 1 планиметра (рис. 15.2) закреплен груз с иглой 3, представляющей полюс Оп планиметра. Вторым концом полюсный рычаг шарнирно входит в гнездо 10 корпуса счетного механизма, установленного на обводном рычаге. Обводный шпиль 6, укреплен-
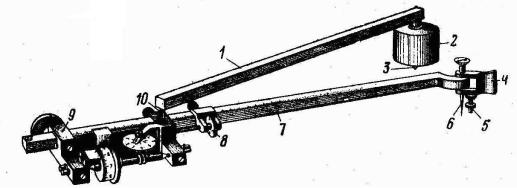
ный на обводном рычаге, представляет обводную точку (марку) М (см. рис. 15.4, б). Рабочий радиус R обводного рычага равен расстоянию АМ между центром шарнира и обводной точкой М (см. рис. 15.4, а) . Этот радиус можно изменить перемещением корпуса счетного механизма вдоль обводного рычага (рис. 15.3), а величину радиуса отсчитать по шкале на обводном рычаге и верньеру счетного механизма. В нашем примере (см. рис. 15.3) R = 1713.
|
Рис. 15.2. Полярный планиметр: |
||||
|
1 |
– |
полюсный рычаг; 2 – |
груз; 3 – игла; 4 – ручка; 5 – опорный штифт; |
|
|
6 |
– обводный шпиль; 7 – |
обводный рычаг; 8 – |
установочный винт; |
|
|
9 |
– |
опора корпуса счетного механизма; 10 – |
гнездо соединения рычагов |
Отсчет по шкалам счетного механизма содержит четыре цифры (см. рис. 15.3). Здесь отсчет u = 3684, где 3 – отсчет по циферблату оборотов счетного колеса; 684
– отсчет по шкале счетного колеса относительно нулевого штриха верньера (68 – номер штриха расположенного ниже нуля верньера; 4 – номер совмещенного штриха верньера).
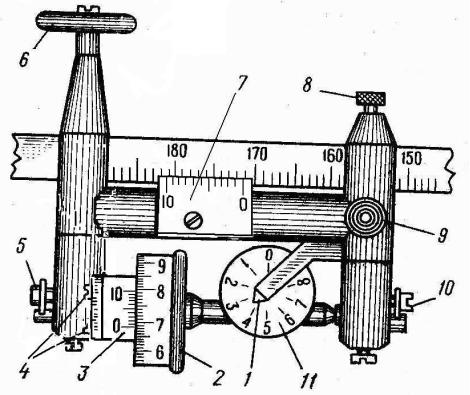
Рис. 15.3. Счетный механизм планиметра:
1 – указатель; 2 – счетное колесо; 3 – верньер счетного механизма; 4 – винты регулировки зазора между верньером и сетным колесом; 5, 10 – винты регулировки счетного колеса; 6 – опорный ролик; 7 – верньер шкалы радиуса планиметра; 8 – закрепительный винт корпуса счетного механизма; 9 – гнездо соединения рычагов; 11 – циферблат счетчика оборотов счетного колеса
П о в е р к и п л а н и м е т р а
До начала работ планиметр необходимо проверить на комплектность и устранить обнаруженные механические неисправности, затем выполнить следующие поверки устройства:
1.Счетное колесо должно свободно вращаться при незначительном люфте и
снебольшим (0,1– 0,2 мм) зазором относительно пластинки верньера. При юсти-
ровке вращают два осевых винта 5 и 10 (см. рис. 15.3), в отверстия которых входят конические концы оси счетного колеса.
2.Ось счетного колеса должна быть параллельна прямой, проходящей через обводный шпиль(или метку) и центр шарнира. Для поверки контур обводят шпи-
лем (маркой М) несколько раз в положении планиметра МЛ «счетный механизм слева от фигуры» (см. рис. 15.5, а) и столько же раз в положении МП «счетный механизм справа от фигуры», не меняя точки полюса О. Если средние разности отсчетов nМЛ и nМП различаются в пределах точности измерений планиметром, то
условие считается выполненным. Для юстировки исправительным винтом изменяют угол между корпусом счетного механизма и обводным рычагом.
Рис. 15.4. Вторая поверка планиметра (а); допустимые углы между рычагами (б)
При работе с неотъюстированным на данное условие планиметром каждую фигуру следует обводить при двух положениях планиметра – ПП и ПЛ и за окончательный результат принимать среднее.
Для измерения площади план кладут на расположенную горизонтально чертежную доску с гладкой поверхностью. Полюс полярного планиметра можно закреплять на плане в положении вне контура или в положении внутри контура, предпочтительное положение полюса – вне контура. Выбирают положение полюса так, чтобы при обводе контура угол β между рычагами (см. рис. 15.4, б) не был меньше 30 и больше 150°. Обводную точку М совмещают с какой-либо точкой К контура. По счетному механизму берут отсчет u1 и записывают в таблицу 15.1, затем контур плавно обводят точкой М и завершают обвод в точке К и берут отсчет u2 (желательно обводить против часовой стрелки, в этом случае последовательные значения отсчетов ui уменьшаются и это удобно для вычислений). Разность отсчетов u1 – u1 = n1 представляет площадь в делениях планиметра.
Продолжают обводы, берут отсчеты ui (см. табл. 15.1) и вычисляют разности отсчетов ni, которые не должны различаться между собой более чем на две единицы при n ≤ 200, на четыре при n ≤ 1000, на шесть при n ≤ 2000. Вычисляют среднюю площадь n в делениях планиметра.
Если плюс расположен вне фигуры, ее площадь в масштабе плана вычисляется по формуле
если же полюс находится внутри фигуры, то площадь вычисляется по формуле
|
Р = с n + Q , |
(15.6) |
|
|
где с – |
цена деления планиметра; |
|
|
Q – |
постоянное слагаемое (обе величины зависят от масштаба плана и радиуса |
планиметра);
n = u i – u i+1 – разность начального и конечного отсчетов при одном обводе замкнутого контура.
Таблица 15.1.
Определение постоянных планиметра с и Q. На плане данного масштаба вы-
бирают простую фигуру с известной площадью Р, например квадрат координатной сетки 10×10 см или два таких квадрата и в положении “ полюс вне контура” 4–5 раз обводят планиметром контур, находят среднюю разность n и цену деления планиметра
Для определения постоянной Q выбирают фигуру, которую можно обвести с полюсом вне ее и внутри. Поместив полюс внутри фигуры получим Р1 = с n1 + Q , а установив полюс вне фигуры найдем Р2 = с n2 и, следовательно,
П р и м е р 1. Определить цену деления планиметра при радиусе R = 2816, если на плане масштаба 1 : 1000 квадрат 10×10 см соответствует площади на местности
Р= d2 М2 = 0,12 ·10002 = 10 000 м2 = 1 га.
Ре ш е н и е. Четырехкратным обводом этого контура с полюсом вне контура
получена средняя разность отсчетов n = 1013 (см. табл. 15.1). Цена деления пла-
ниметра с = 10 000 / 1013 = 9,8717 м2 / 1 деление = 1 / 1013 = 0,0009871 га / 1 деле-
ние. Такая “ некруглая” цена деления осложняет устные вычисления по формулам
(15.39) и (7.40).
Для изменения цены деления планиметра изменяют радиус R обводного рычага
|
до значения R0, рассчитанного по формулам |
|
|
R0 = R (с0 / с) или R0 = R (n / n0 ), |
(15.9) |
где n0 – средняя разность отсчетов, отвечающая значению с0.
В нашем примере круглое значение с0 = 10 м2 / 1 деление, ему соответствует ра-
диус R0 = 2816 (10 / 9,8717) = 2853 или R0 = 2816 (1013 / 1000) = = 2853. После ус-
тановки радиуса R0 проверяют новую цену деления несколькими обводами контура.
Зависимость цены деления планиметра от масштаба плана. Если при мно-
гократном обводе контура, например квадрата размером 10×10 см, средняя разность отсчетов nср = 1000 ± 2 деления, то практически точные значения цены деления планиметра (формула 15.7) будут равны:
–с = 0,1 га/дел. для плана масштаба 1:10 000;
–с = 10 м2/дел. (0,001 га/дел) для плана масштаба 1:1000;
–с = 2,5 м2/дел. (0,00025 га/дел) для плана масштаба 1:500.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
