Как найти площадь резистора

1.Расчет
тонкопленочных резисторов

К пленочным резисторам предъявляются следующие
основные требования: стабильность во времени, малая занимаемая площадь на
подложке, низкий температурный коэффициент сопротивления, требуемая мощность
рассеяния, низкий уровень шумов, малые значения паразитных параметров.

Исходные данные для расчета резисторов приведены в
таблице 1.

Исходные данные для расчета резисторов

Таблица 1.

№	Схемное обознач.	Номинал, R, кОм	Относит. погр-ть номинала, γR	Максим. Мощность рассеян. Р, Вт	Максим. Раб. темпер. tmax, 0С	Предполаг. длит. Работы, ч	Относит. погреш. сопр-я, γρ0	Абсолют. погр-ть геом. параметров ∆l, ∆b,м
1	R1	6.8	0.15	0.02	80	10000	0.05	10^(-5)
2	R2	68
3	R3	0.39
4	R4	10
5	R6	18
6	R7	1.8
7	R8	100
8	R9	0,12
9	R10	150
10	R11	150

Все резисторы разбиваем на две группы: R3, R7, R9 – первая
группа;R1, R2, R4, R6, R8, R10, R11 – вторая группа.

1.1.Расчет первой группы резисторов

Для первой группы резисторов выбираем тантал

–
удельное поверхностное сопротивление ρ0=100 Ом

– удельная
мощность рассеяния Р0=3 Вт/см²

–
ТКС αR=-2*10^-4

Температурная погрешность зависит от ТКС материала
пленки и диапазона рабочих температур: γt=αR( tmax -20)= -2*10^(-4)(80-20)=
-0.012.

Допустимая погрешность коэффициента формы:

γкфдоп=γR-γρ0-γст-γt-γк ,

где
γст=0,03
– погрешность, обусловленная старением пленки;

     
γк=0,01
– погрешность переходных сопротивлений контактов.

γкфдоп=0,15-0,05-0,03-0,012-0,01=0,048

R9=120
Ом

1.Вычисляем
коэффициент формы Кф=R/ρ0=120/100=1,2

2.Определяем
расчетную ширину резистора:

bточн=(∆b+∆l/Кф)/γкфдоп=(10+10/1.2)/0.048=382 мкм

bp=Pρ0/P0R=0.02*100/300*120=56 мкм

3.Выбираем
максимальную ширину резистора:

b=382
мкм

4.Расчетная
длина резистора равна: lрасч=bКф=459
мкм

5.Полная
длина резистора равна: lполн=lрасч+2L=459+200=658 мкм

6.Площадь
резистора равна: S=lполнb=0.658*0.382=0.251 мм²

R7=1,8
кОм

1.Вычисляем
коэффициент формы Кф=R/ρ0=1800/100=18

2.Определяем
расчетную ширину резистора:

bточн=(∆b+∆l/Кф)/γкфдоп=(10+10/18)/0.048=220 мкм

bp=Pρ0/P0R=0.02*100/300*1800=3,7
мкм

3.Выбираем
максимальную ширину резистора:

b=220
мкм

4.Расчетная
длина резистора равна: lрасч=bКф=3960
мкм

5.Полная
длина резистора равна: lполн=lрасч+2L=3960+400=4360 мкм

6.Площадь
резистора равна: S=lполнb=4,360*0.22=0.959 мм²

R3=390
Ом

1.Вычисляем
коэффициент формы Кф=R/ρ0=390/100=3,9

2.Определяем
расчетную ширину резистора:

bточн=(∆b+∆l/Кф)/γкфдоп=(10+10/3,9)/0.048=262 мкм

bp=Pρ0/P0R=0.02*100/300*390=17
мкм

3.Выбираем
максимальную ширину резистора:

b=262
мкм

4.Расчетная
длина резистора равна: lрасч=bКф=1021
мкм

5.Полная
длина резистора равна: lполн=lрасч+2L=1021+200=1221 мкм

6.Площадь
резистора равна: S=lполнb=1,221*0.262=0.32 мм²

1.2.Расчет второй группы
резисторов

Для второй группы резисторов выбираем кермет К-50С с
параметрами:

–
удельное поверхностное сопротивление ρ0=6000 Ом

–
удельная мощность рассеяния Р0=2 Вт/см²

–
ТКС αR=-3*10^-4

Температурная погрешность зависит от ТКС материала
пленки и диапазона рабочих температур: γt=αR( tmax -20)= -3*10^(-4)(80-20)= -0.018.

Допустимая погрешность коэффициента формы:

γкфдоп=γR-γρ0-γст-γt-γк ,

где
γст=0,03
– погрешность, обусловленная старением пленки;

     
γк=0,01
– погрешность переходных сопротивлений контактов.

γкфдоп=0,15-0,05-0,03-0,018-0,01=0,042

R1=6,8 кОм

1.Вычисляем
коэффициент формы Кф=R/ρ0=6800/6000=1,13

2.Определяем
расчетную ширину резистора:

bточн=(∆b+∆l/Кф)/γкфдоп=(10+10/1,13)/0.042=449 мкм

bp=Pρ0/P0R=0.02*6000/200*6800=88
мкм

3.Выбираем
максимальную ширину резистора:

b=449
мкм

4.Расчетная
длина резистора равна: lрасч=bКф=507
мкм

5.Полная
длина резистора равна: lполн=lрасч+2L=507+200=707 мкм

6.Площадь
резистора равна: S=lполнb=0,707*0.449=0.317 мм²

R2=68
кОм

1.Вычисляем
коэффициент формы Кф=R/ρ0=68000/6000=11,3

2.Определяем
расчетную ширину резистора:

bточн=(∆b+∆l/Кф)/γкфдоп=(10+10/11,3)/0.042=259 мкм

bp=Pρ0/P0R=0.02*6000/200*68000=8,8
мкм

3.Выбираем
максимальную ширину резистора:

b=259
мкм

4.Расчетная
длина резистора равна: lрасч=bКф=2927
мкм

5.Полная
длина резистора равна: lполн=lрасч+2L=2927+200=3127 мкм

6.Площадь
резистора равна: S=lполнb=3,127*0.259=0.81 мм²

R4=40
кОм

1.Вычисляем
коэффициент формы Кф=R/ρ0=40000/6000=6,67

2.Определяем
расчетную ширину резистора:

bточн=(∆b+∆l/Кф)/γкфдоп=(10+10/6,67)/0.042=274 мкм

bp=Pρ0/P0R=0.02*6000/200*40000=15
мкм

3.Выбираем
максимальную ширину резистора:

b=274
мкм

4.Расчетная
длина резистора равна: lрасч=bКф=1828
мкм

5.Полная
длина резистора равна: lполн=lрасч+2L=1828+200=2028 мкм

6.Площадь
резистора равна: S=lполнb=2,028*0.274=0.556 мм²

R6=18
кОм

1.Вычисляем
коэффициент формы Кф=R/ρ0=18000/6000=3

2.Определяем
расчетную ширину резистора:

bточн=(∆b+∆l/Кф)/γкфдоп=(10+10/3)/0.042=317 мкм

bp=Pρ0/P0R=0.02*6000/200*18000=33
мкм

3.Выбираем
максимальную ширину резистора:

b=317
мкм

4.Расчетная
длина резистора равна: lрасч=bКф=951
мкм

Определение
габаритов печатной платы

Основные
конструктивные параметры элементной
базы:

Наименование элемента	Кол-во	Вариант установки	Установочная площадь, мм2
Конденсаторы: К50-16 К10-7в	4 4	II-в II-в	427,75 353,75
Микросхемы: К176ИЕ12 К176ИЕ13 К514ИД2 К176ЛА7 К176ЛЕ5	1 1 1 1 1	VIII-a VIII-a VI-б VIII-a VIII-a	141,25 141,25 241,5 146,25 146,25
Резистор КИМ Резистор СП3-9а	26 1	II-в II-в	812,5 29,7
Диод КД103А	11	II-в	385
Тиристор КУ101А	1	V-в	93,6
Транзистор КТ315А Транзистор КТ315В Транзистор КТ315Г	6 1 5	II-в II-в II-в	129,6 21,6 108

Площадь, занимаемая одним конденсатором
(микросхемой), определяется по формуле:

S=
B·L,

где B и L – габаритные размеры конденсатора
(микросхемы).

Для конденсатора

К50-16
: S_к1=6,5·13,5+13,5·8+15,5·8+13,5·8=427,75
(мм²)

К10-7в: S_к2=6,5·8,5·2+9·13,5·2=353,75
(мм²)

Для микросхемы

К176ИЕ12: S_м/сх=7,3·19,35=141,25
(мм²)

К176ИЕ13: S_м/сх=7,3·19,35=141,25
(мм²)

К514ИД2: S_м/сх=13,8·17,5=241,5
(мм²)

К176ЛА7: S_м/сх=7,5·19,5=146,25
(мм²)

К176ЛЕ5: S_м/сх=7,5·19,5=146,25
(мм²)

Для транзистора:

КТ315А: S_м/сх=7,2·3·6=129,6
(мм²)

КТ315В: S_м/сх=7,2·3=21,6
(мм²)

КТ315Г: S_м/сх=7,2·3·5=108
(мм²)

Площадь, занимаемая одним резистором(диодом),
определяется по формуле:

S=
D·l,

где D и l –
габаритные размеры резистора.

Для резистора:

КИМ
: S_р=2,5·12,5·26=812,5
(мм²)

СП3-9а: S_р=2,2·13,5=29,7
(мм²)

Для диода:

КД103А: S_д=2,8·12,5·11=385
(мм²)

Для
тиристора:

КУ101А S_т=11,7·8=93,6
(мм²)

Определим общую площадь, занимаемую
всеми ЭРЭ на печатной плате:

,

где
N
– количество ЭРЭ одного типа,
устанавливаемых на печатную плату.

S=427,75+353,75+141,25+141,25+241,5+146,25+146,25+812,5+29,7+385+93,6+129,6+21,6+108=3578
(мм²)

С
учетом рекомендуемого значения
коэффициента заполнения площади печатной
платы для бытовой РЭА, равного 0,6, получим
значение площади

мм².

Рассмотрено
несколько возможных вариантов соотношения
сторон печатной платы (60×110, 65×100, 80×80) и
по ГОСТ 10317-79 был выбран следующий –
60×110 мм².

Для
определения объема печатной платы
необходимо знать ее высоту, которая
определяется с учетом превышения над
плоскостью платы самого высокого ЭРЭ
плюс
толщина основания ПП.
Высота рассматриваемой печатной платы
равна (высота пьезоэлемента ZQ1,
равная 19,7 мм, плюс толщины платы, равная
1,5 мм). Тогда

V_пп
= 60·110·(19,7+1,5)=
60·110·21,2=139·10³мм³.

РАСЧЁТ ПЕЧАТНОГО
МОНТАЖА

1Выбор метода
изготовления и класса точности печатной
платы

Для соединения
элементов электрической схемы электронного
кубика между собой в качестве базовой
несущей конструкции выбираем двухстороннюю
печатную плату (размером 4060),
выполненную комбинированным позитивным
методом из фольгированного стеклотекстолита
СФ-2Н-50Г-1,5 (ГОСТ 10316-78).

Учитывая
невысокий уровень насыщенности печатной
платы, выбираем по ГОСТ 23751 – 86 третий
класс точности.

2 Расчёт печатного
монтажа

Исходные данные:

– плата печатная
двухсторонняя;

– метод изготовления
– комбинированный позитивный;

– линейные размеры
платы, мм 40·60·1,5;

– материал –
стеклотекстолит фольгированный
СФ-2Н-50Г-1,5;

– толщина фольги
h, мм 0,05;

– допустимая
плотность тока j_доп,
А/мм2 38;

– удельное
сопротивление ρ, Ом·мм2/м 0,0175.

– шаг координатной
сетки, мм 1,25.

Основные
конструктивные параметры печатных плат
для третьего класса точности (ГОСТ
23751-86):

– минимальное
значение номинальной ширины проводника
t_1min,
мм 0,25;

– номинальное
расстояние между проводниками S, мм 0,25;

– гарантийный
поясок b_м,
на наружном слое, мм 0,10;

– то же, на внутреннем
слое, мм 0,05;

– допуск на отверстие
d,
мм
;

– допуск на ширину
проводника без покрытия t,
мм
;

– допуск на
расположение отверстий _d,
мм 0,08;

– допуск на
расположение контактных площадок _p,
мм 0,20;

– допуск на отверстие
d,
мм;

– допуск на
расположение проводников на ДПП l,
мм 0.03;

2.1 Расчет по
постоянному току

Минимальная ширина
печатного проводника по постоянному
току для цепей питания и заземления:

где I_max
– максимальный постоянный ток, протекающий
в проводнике;

i_доп
– допустимая плотность тока, А/мм2;

h – толщина
проводника, мкм.

Максимальный
постоянный ток I_max,
протекающий в проводнике для цепей
питания, равен 31,25 мА. Тогда, получим,

(мм).

Минимальная ширина
проводника, исходя из допустимого
падения напряжения на нем:

,

где 
– удельное объёмное сопротивление,
Ом·мм²/м;

l
– длина проводника, м;

U_доп
– допустимое падение напряжения, В.

Допустимое падение
напряжения не должно превышать 5% от
напряжения питания микросхем, поэтому
принимаем:

U_доп
= 0,05·5=0,25 В.

Тогда

(мм).

Соседние файлы в папке 39 Часы на светодиодных индикаторах

• #

  21.02.2014155.69 Кб57блокпитания.frw

• #

  21.02.201481.17 Кб57Компановка.bak

• #

  21.02.201482.93 Кб62Компановка.cdw

• #
• #
• #
• #
• #
• #
• #
• #

  21.02.201417.31 Кб60спецификация_сб.bak

Решение задач на закон Ома для участка и полной цепи

Решение задач на закон Ома сводится к нахождению одной из трех неизвестных составляющих: тока, сопротивления или напряжения. Сам же закон описывает, как они соотносятся между собой.

Напомним, что согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

Формула закона Ома для участка цепи:

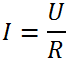
Формула закона Ома для полной цепи:

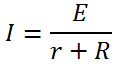Задача 1

Утюг включенный в сеть напряжением 220 В, потребляет ток 1,2 А. Определите сопротивление утюга.

Согласно закону Ома для участка цепи:

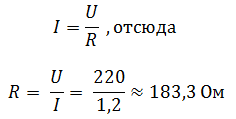
Ответ: R = 183,3 Ом.

Задача 2

К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.

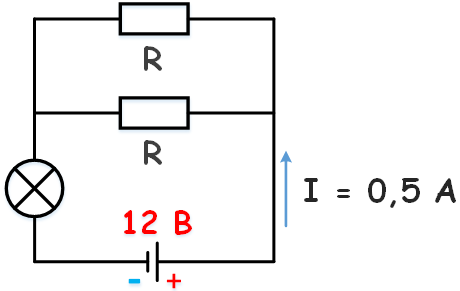
Найдем экв. сопротивление двух параллельно соединённых резисторов:

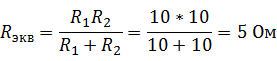
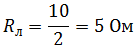
Согласно закону Ома для полной цепи:

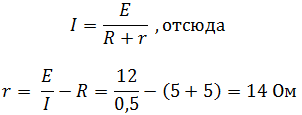
Ответ: r = 14 Ом.

Задача 3

К участку цепи с напряжением 12 В через резистор сопротивлением 2 Ом подключены десять одинаковых лампочек сопротивлением 10 Ом. Найти напряжение на каждой лампочке.

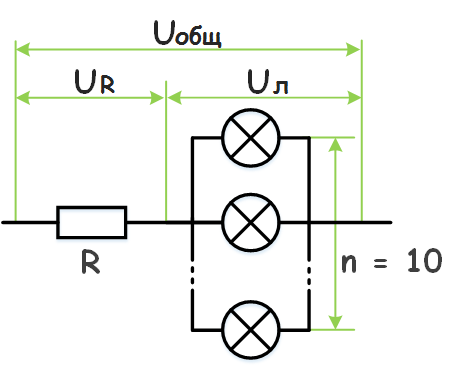
Так как лампочки подключены параллельно, напряжение на них будет одинаковым, согласно закону Ома для участка цепи:

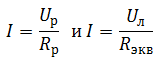
При последовательном соединении ток в цепи общий:

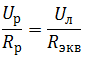
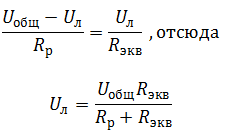
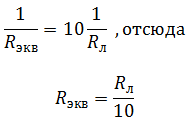
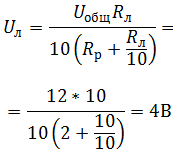
Ответ: Uл = 4 В.

Задача 4

Как определить длину мотка медной проволоки, не разматывая его?

Для решения данной задачи необходимо воспользоваться формулой:

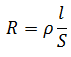
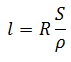
В этой формуле, l – длина проволоки, R – сопротивление, S – площадь поперечного сечения, ρ – удельное сопротивление металлов, в данном случае ρ для меди равно 0.0175 Ом/м.

Сопротивление R проволоки можно измерить с помощью омметра, а площадь S с помощью штангенциркуля, измерив диаметр проволоки и по формуле Πr 2 вычислив ее значение. Значение удельного сопротивления ρ не только для меди, но и других металлов можно найти в справочнике, или тут. Подставив все известные величины в формулу, приведенную выше, получим длину проволоки.

Задача 5

Начертите схему электрической цепи, состоящей из источника тока, выключателя и двух ламп, включенных параллельно. Что произойдет в цепи при перегорании одной лампы?

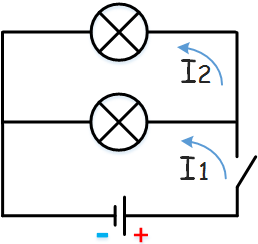
При перегорании одной из лампочек, вторая будет гореть, так как, при параллельном включении проводников токи I₁ и I₂ проходящие через них не зависят друг от друга и при разрыве параллельной цепочки ток продолжает протекать.

Источник

Задачи на закон Ома с решением

Знание закона Ома на сегодняшний день – вопрос общей эрудиции каждого человека. В сегодняшней статье займемся решением задач по теме «закон Ома».

Подписывайтесь на наш телеграм и получайте интересные новости каждый день! А если хотите получить скидку и не упустить выгоду – загляните на наш второй канал с приятными акциями и бонусами для клиентов.

Закон Ома: задачи с решением

Для новичков, которые только начинают решать задачи по физике, мы подготовили специальную памятку и собрали вместе более 40 формул по разным темам. Берите и пользуйтесь!

Задача на закон Ома №1

Определите силу тока в медном проводнике сеченим 0,5 мм2, если длина проводника 100 м, а напряжение на его концах равно 6,8 В.

Сначала запишем закон Ома:

В данном случае, чтобы найти силу тока I, нужно определить сопротивление R. Используем формулу с удельным сопротивлением и перепишем выражение для закона Ома:

Осталось подставить числа и рассчитать:

I = 6 , 8 · 0 , 5 0 , 017 · 100 = 2 А

Значение удельного сопротивления «ро» для меди берется из таблиц. Для меди ρ = 0 , 017 О м · м м 2 м

Задача на закон Ома №2

По вольфрамовой проволоке длиной 3 м протекает электрический ток силой 0,04 А. Проволока находится под напряжением 5 В. Определите величину площади поперечного сечения проволоки.

Выразим площадь поперечного сечения проводника из формулы для сопротивления:

Сопротивление R найдем из закона Ома:

Подставим выражение для R в формулу для S и рассчитаем:

S = ρ l · I U = 0 , 055 · 3 · 0 , 04 5 = 0 , 0013 м м 2

Ответ: 0 , 0013 м м 2

Задача на закон Ома №3

Каково напряжение на неоднородном участке цепи?

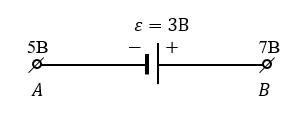
По закону Ома для неоднородного участка цепи:

Считая началом участка точку A, а концом – точку B, и беря поэтому ЭДС со знаком плюс (внутри источника направление тока от отрицательного полюса к положительному), получаем:

U A B = φ A — φ B + ε = 5 — 7 + 3 = 1 В

Нужно больше примеров решений задач? Вы найдете их в нашем блоге!

Задача на закон Ома №4

Какова сила тока в резисторе, если его сопротивление 12 Ом, а напряжение на нем 120 В?

Это простейшая задача на закон Ома для участка цепи, которая решается в одно действие. Просто записываем закон Ома и производим расчет:

Ответ: 10 А.

Задача на закон Ома №5

Источник постоянного тока с ЭДС E = 12 В и внутренним сопротивлением г = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить силу тока в цепи I, падение напряжения UR на внешнем участке и падение напряжения Ur на внутреннем участке цепи.

Это задача на закон Ома для полной цепи. По закону Ома для замкнутой цепи:

I = ε R + r = 12 9 + 1 = 1 , 2 А

Падение напряжения на внешнем участке цепи:

U R = I · R = ε R R + r = 12 · 9 9 + 1 = 10 , 8 В

Падение напряжение на внутреннем участке цепи:

U r = ε — U R = 12 — 10 , 8 = 1 , 2 В

Ответ: 1,2 А; 10,8 В; 1,2 В.

Школьный учитель Георг Симон Ом открыл свой закон в 1826 году. Подробнее об истории открытия и самом законе Ома читайте в нашем блоге.

Вопросы на закон Ома

Вопрос 1. Сформулируйте закон Ома для однородного участка цепи.

Ответ. Закон Ома для однородного участка цепи нласит:

Ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.

Вопрос 2. Сформулируйте закон Ома для замкнутой цепи.

Ответ. Закон Ома для замкнутой цепи гласит:

Величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.

Вопрос 3. От чего зависит сопротивление цепи?

Ответ. Сопротивление вещества обусловлено колебанием атомов кристаллической решетки.

• температуры;
• материала;
• поперечного сечения проводника.

Вопрос 4. Зависит ли сопротивление от напряжения и силы тока?

Ответ. Нет. Сопротивление не зависит от напряжения и силы тока в проводнике.

Вопрос 5. Всегда ли соблюдается закон Ома?

Ответ. Нет, не всегда. Например, закон Ома не действует при низких температурах для веществ, обладающих сверхпроводимостью.

Проблемы с учебой? Обращайтесь в профессиональный сервис для студентов за квалифицированной помощью.

Источник