Как найти площадь робота

Перейти к содержимому Меню Закрыть

ГДЗ, ответы, контрольные работы, решение заданий, тесты на Знания.ком

Искать:

Знания.ком

Меню

Знания.ком

Искать:

Меню

ГДЗ, ответы, контрольные работы, решение заданий, тесты на Знания.ком

Искать:

Кнопка

Главная страница

Вопросы

как найти площадь робота?

17 просмотров10.07.2022Геометрия

admin304.70K 10.07.2022 0 комментариев

как найти площадь робота?

Регистрация или Вход

Вопросы

Информатика. 9 класс. 3 ответа | 0 Голосов

характеристика автора романа Бедная Лиза 2 ответа | 0 Голосов

Пример со скрытым числом 1 ответ | 0 Голосов

Разработка на Python 1 ответ | 0 Голосов

Обществознание законы 1 ответ | 0 Голосов

Источник

Главная
Блог
Робот, который поможет разобраться с «площадью» и «периметром»

Робот, который поможет разобраться с «площадью» и «периметром»

Многим второклашкам тема «Площадь и периметр квадрата и прямоугольника» даётся очень непросто. Как раз для таких ребят мы подготовили шаблон и инструкцию, как с помощью робота разобраться в этой сложной теме.

Скачать шаблон.

Дата публикации: 2019-10-14 09:55

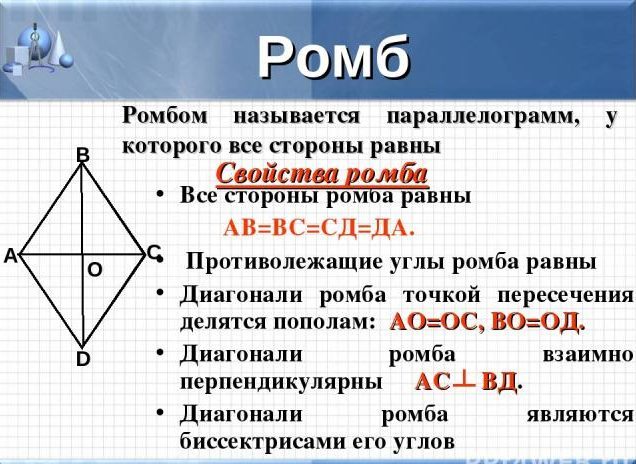
Как вычислить площадь ромба – свойства фигуры

Прежде, чем вычислить площадь ромба, лучше ознакомиться со свойствами данной фигуры. Ведь благодаря знанию этих характеристик дальше проще будет доказать вероятность той или иной формулы. Ранее упоминалось уже, что такое ромб. Он представляет собой фигуру с равными абсолютно всеми сторонами, равными противоположными острыми и тупыми углами, но не прямыми.

Ромб имеет следующие свойства:

у него все стороны между собой равны
углы, лежащие напротив друг друга, тоже равны
диагонали данной фигуры являются биссектрисами, в точке пересечения делятся на равные отрезки
также диагонали пересекаются в центре ромба и под прямыми углами
противоположные стороны фигуры не могут пересекаться, даже если продлить лучи они же параллельны, как у параллелограмма.

Свойства фигуры

ВАЖНО: Обратите внимание, что ромб можно разбить на четыре прямоугольных треугольника, которые будут между собой равны по площади, или на два равносторонних идентичных треугольника, см. изображение выше.

Как вычислить площадь ромба?

Итак, давайте выясним, как вычисляется площадь ромба. Давайте воспользуемся для этого формулой площади прямоугольника, где:

S = a • b, где a, b – стороны прямоугольника.

Чтобы было понятно, как вывести из этой формулы, формулу площади ромба, смотрите объяснение:

Нарисуйте ромб, проведите высоту к основанию ромба BH.
Из точки D на линию AD проведите тоже высоту CH1.
Выходит что треугольник ABH и треугольник CH1D между собой равны по двум общим сторонам, ∠ углу между ними.
Значит AH=DH1. Площадь образовавшегося квадрата будет равна площади ромба
А значит BH • HH1 – это и есть площадь ромба, другими словами произведение высоты BH ромба на сторону AD и будет S площадью ромба, поскольку HH1 = BC, а BH – это высота.

Высота ромба

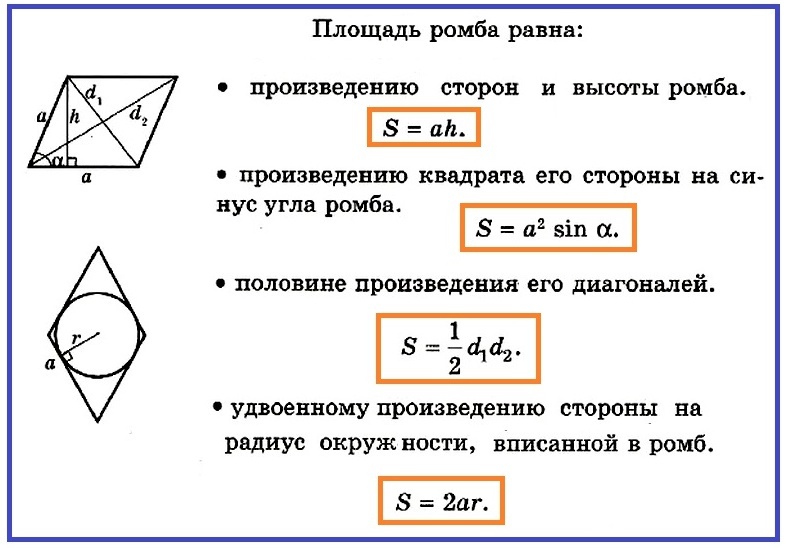
Из доказательства вытекает, что:

S ромба = a • h и измеряется в квадратных единицах.

Как найти площадь ромба, зная угол и сторону геометрической фигуры?

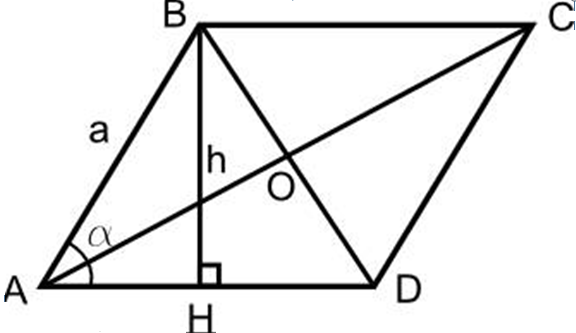
Теперь мы знаем, как выглядит формула площади ромба, можем по этой же формуле найти и S площадь ромба, зная чему равна сторона ромба и ∠ угол, например, острый у основания, как на фото ниже.

S = a • h

Но в нашем случае нам неизвестна высота ромба, ее следует найти. Для этого придется рассмотреть треугольник прямоугольный, который получился, когда была проведена высота к основанию ромба.

В этом треугольнике известна гипотенуза и ∠α. Чтобы вычислить площадь всей фигуры, понадобится найти высоту. А h = a • sin∠α. Значит S площадь равностороннего параллелограмма (ромба) равняется:

S = a • a • sin∠α = a² • sin∠α

Площадь фигуры

Как вычислять площадь ромба, зная его диагонали?

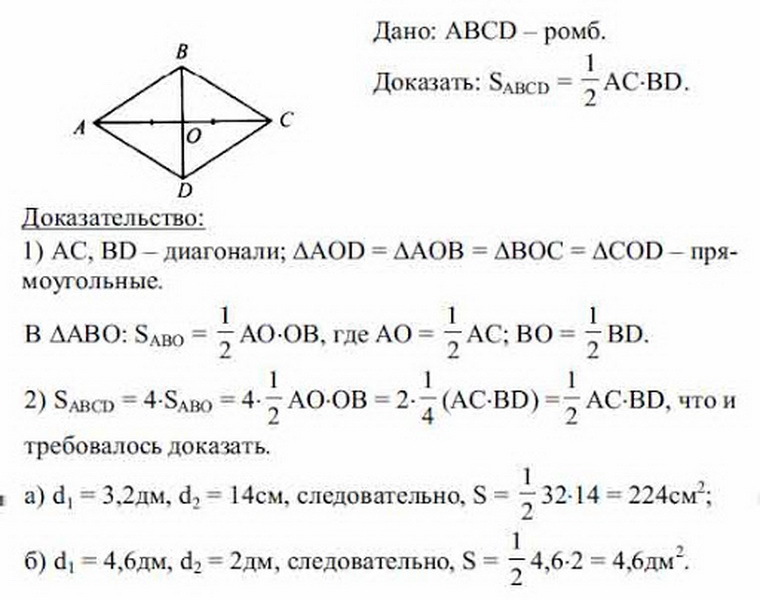
Чтобы узнать формулу площади ромба, когда известны только (a, b) диагонали, следует рассмотреть следующий пример. Дано BCDA – ромб и знаем чему равны диагонали. Теперь следует найти S площадь равностороннего параллелограмма по величинам диагоналей.

Ранее уже рассматривали свойства ромба. Диагонали ромба равны, в точке пересечения делятся на равные отрезки. Из этого следует, что все треугольники, которые вписаны в фигуру в результате пересечения обеих диагоналей тоже равны между собой и они прямоугольные (по трем сторонам). Чтобы найти площадь ромба, достаточно найти площадь одного треугольника и полученные данные умножить на 4.

Итого выходит, что:

S ромба = 4 (1/2 AO • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) = 4 • 1/8 AC • BD = 1/2 BD • AC, итого площадь S ромба будет = произведению a • b (диагоналей) деленное на два: S = 1/2 a • b

Площадь фигуры

Как вычислять площадь ромба, зная его сторону и радиус вписанной в него окружности?

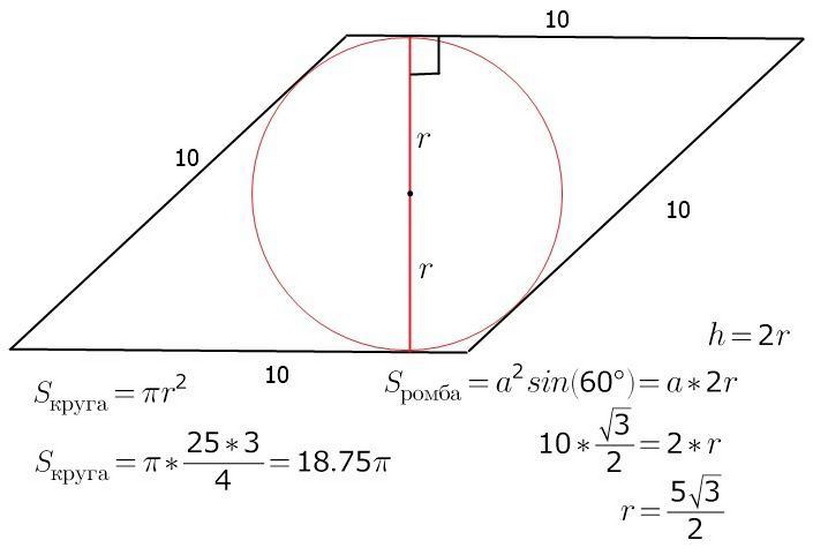
Площадь ромба можно рассчитать, зная r – радиус и a – длину стороны фигуры. Уже известно, что S – площадь фигуры будет равна произведению b – стороны на h – высоту. Через центр окружности, он же будет являться и центром пересечения a, b – диагоналей ромба. Проведите высоту и одновременно диаметр ромба. На изображении видно, что высота фигуры – это два радиуса окружности. Теперь легко будет найти и площадь самого ромба:

S = a • h = a • 2r

Ниже смотрите пример задачи на данную тематику.

Площадь ромба

Еще смотрите подобные статьи на данную тематику здесь:

Площадь прямоугольника, как найти?
Как найти площадь круга?
Площадь квадрата – формулы.

Видео: Пример того, как вычислять площадь ромба

Источник

Площадь фигуры ограниченной линиями

Что умеет?

Находит точки пересечения указанных кривых линий
Умный робот определяет области, где лежат фигуры, чтобы вычислить их площади. Она делает это, находя точки, где графики пересекаются.
Помогает находить площади под графиками, вычисляя интегралы.

Примеры кривых

С осями ординат x и y
```
y = x^2 + 1
y = 0
x = -1
x = 2
```
Графики, заданные неявным образом
```
y = 3
xy = 2
y^2 - x^2 = 3
```
Две окружности
```
x^2 + y^2 = 4
x^2 + y^2 = 9
```
В полярных координатах
```
r = 2(1 - cos(p))
r = 2
```
Парабола и прямая линия
```
y = (x + 2)^2
y = 4
```
```
y = (x + 2)^2
y = 1 - x
```
```
y = x^2
x + y = 2
```
Корень квадратный
```
y = x^2
y = sqrt(x)
```
С экспонентой и численным решением
```
y = (2x+3)*e^(-x)
x^2 = y
```
Параметрически-заданная функция
```
x = 2(t - sint)
y = 3(1 - cost)
```

Указанные выше примеры содержат также:

модуль или абсолютное значение: absolute(x) или |x|
квадратные корни sqrt(x),
кубические корни cbrt(x)
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
показательные функции и экспоненты exp(x)
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x)
натуральные логарифмы ln(x),
десятичные логарифмы log(x)
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x)
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x)
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x)
знак числа:
sign(x)
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x)
Факториал от x:
x! или factorial(x)
Гамма-функция gamma(x)
Функция Ламберта LambertW(x)
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)

Правила ввода

Можно делать следующие операции

2*x: – умножение
3/x: – деление
x^2: – возведение в квадрат
x^3: – возведение в куб
x^5: – возведение в степень
x + 7: – сложение
x – 6: – вычитание
Действительные числа: вводить в виде 7.5, не 7,5

Постоянные

pi: – число Пи
e: – основание натурального логарифма
i: – комплексное число
oo: – символ бесконечности

Источник

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 – 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 – 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 – 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник