
{S = a^2 cdot sin (alpha)}
На этой странице мы предлагаем вам 7 формул площади ромба. Для каждой формулы можно воспользоваться онлайн калькулятором и мгновенно получить результат, не прибегая к помощи обычного калькулятора
Содержание:
- калькулятор площади ромба
- формула площади ромба через сторону и угол
- формула площади ромба через сторону и высоту
- формула площади ромба через диагонали
- формула площади ромба через угол и диагональ из угла
- формула площади ромба через угол и противолежащую диагональ
- формула площади ромба ромба через радиус вписанной окружности и угол
- формула площади ромба через радиус вписанной окружности и сторону
- примеры задач
Формула площади ромба через сторону и угол

S = a^2 cdot sin (alpha)
a – сторона ромба
α – угол между сторонами ромба
Формула площади ромба через сторону и высоту

S = a cdot h
a – сторона ромба
h – высота ромба
Формула площади ромба через диагонали
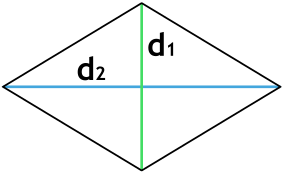
S = dfrac{d_1 cdot d_2}{2}
d1 и d2 – диагонали ромба
Формула площади ромба через угол и диагональ из угла
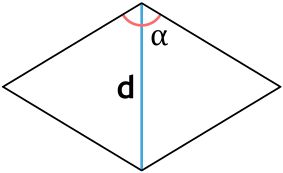
S = dfrac{d^2}{2} cdot \tg(dfrac{alpha}{2})
d – диагональ ромба
α – угол между сторонами ромба, из которого выходит диагональ
Формула площади ромба через угол и противолежащую диагональ

S = dfrac{d^2}{2} cdot ctg(dfrac{alpha}{2})
d – диагональ ромба, противоположная углу α
α – угол между сторонами ромба
Формула площади ромба через радиус вписанной окружности и угол
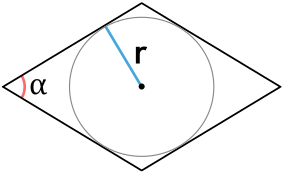
S = dfrac{4r^2}{sin(alpha)}
r – радиус окружности
α – угол между сторонами ромба
Формула площади ромба через радиус вписанной окружности и сторону
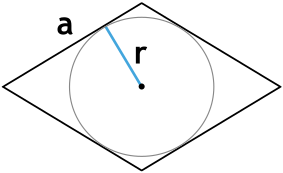
S = 2ar
r – радиус окружности
a – сторона ромба
Примеры задач на нахождение площади ромба
Задача 1
Найдите площадь ромба если его диагонали равны 34 и 4.
Решение
Для решения задачи воспользуемся формулой площади ромба через диагонали.
S = dfrac{d_1 cdot d_2}{2} = dfrac{34 cdot 4}{2} = 68 : см^2
Ответ: 68 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь ромба если его диагонали равны 4 и 6.
Решение
Задача аналогична предыдущей.
S = dfrac{d_1 cdot d_2}{2} = dfrac{4 cdot 6}{2} = 12 : см^2
Ответ: 12 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь ромба стороны которого равны 5, а высота равна 4.
Решение
Воспользуемся формулой площади ромба через высоту и сторону.
S = a cdot h = 5 cdot 4 = 20 : см^2
Ответ: 20 см²
Проверим полученный ответ на калькуляторе .
Ромб – это геометрическая фигура; параллелограмм, имеющие 4 равные стороны.
-
Формула вычисления площади
- По длине стороны и высоте
- По длине стороны и углу
- По длинам диагоналей
- Примеры задач
Формула вычисления площади
По длине стороны и высоте
Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a ⋅ h

По длине стороны и углу
Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:
S = a 2 ⋅ sin α

По длинам диагоналей
Площадь ромба равна одной второй произведения его диагоналей.
S = 1/2 ⋅ d1 ⋅ d2

Примеры задач
Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.
Решение:
Используем первую формулу, рассмотренную выше: S = 10 см ⋅ 8 см = 80 см2.
Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.
Решение:
Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см)2 ⋅ sin 30° = 36 см2 ⋅ 1/2 = 18 см2.
Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.
Решение:
Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 ⋅ 4 см ⋅ 8 см = 16 см2.
Как рассчитать площадь ромба
На данной странице калькулятор поможет рассчитать площадь ромба онлайн. Для расчета задайте длину основания, высоту или длины диагоналей и угол между ними.
Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом.
Через сторону и высоту
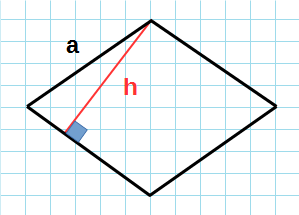
Формула для нахождения площади ромба через сторону и высоту:
a – сторона ромба; h – высота ромба.
Через диагонали
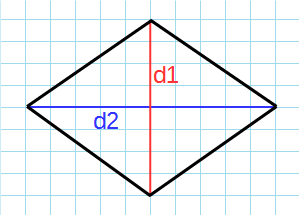
Формула для нахождения площади ромба через диагонали:
d1, d2 – диагонали ромба.
Через сторону и угол
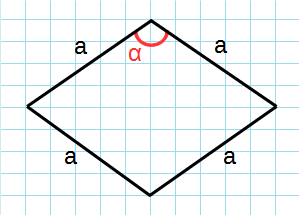
Формула для нахождения площади ромба через сторону и угол:
a – сторона ромба; α – угол между сторонами.
Через угол и диагональ из этого угла
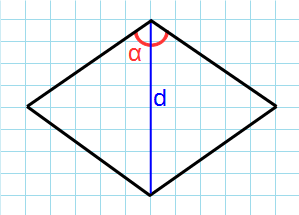
Формула для нахождения площади ромба через угол и диагональ выходящая из этого угла:
d – диагональ ромба; α – угол между сторонами.
Через угол и противолежащию диагональ
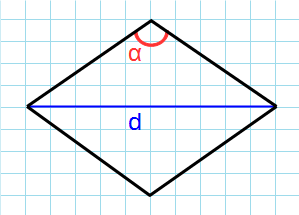
Формула для нахождения площади ромба через угол и диагональ противолежащая углу:
d – диагональ ромба; α – угол между сторонами.
Через угол и радиус вписанной окружности
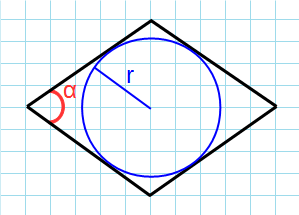
Формула для нахождения площади ромба через угол и радиус вписанной окружности:
r – радиус окружности; α – угол между сторонами.
Через сторону и радиус вписанной окружности
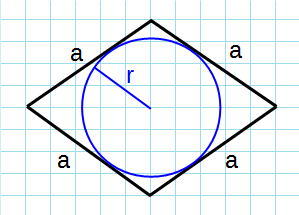
Формула для нахождения площади ромба через сторону и радиус вписанной окружности:
a – сторона ромба; r – радиус вписанной окружности.
Ромб — это параллелограмм, в котором все стороны равны друг другу.
Онлайн-калькулятор площади ромба
Если стороны ромба образуют прямой угол, то получим квадрат.
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.
Площадь ромба, как и площади большинства геометрических фигур, можно найти несколькими способами. Разберемся в их сути и рассмотрим примеры решений.
Формула площади ромба по стороне и высоте
Пусть нам дан ромб со стороной aa и высотой hh, проведенной к этой стороне. Так как ромб это параллелограмм, то его площадь мы находим так же, как и площадь параллелограмма.
S=a⋅hS=acdot h
aa — сторона;
hh — высота, опущенная на сторону aa.
Решим простой пример.
Сторона ромба равна 5 (см.). Высота, опущенная к этой стороне, имеет длину 2 (см.). Найти площадь ромба SS.
Решение
a=5a=5
h=2h=2
Пользуемся нашей формулой и вычисляем:
S=a⋅h=5⋅2=10S=acdot h=5cdot 2=10 (см. кв.)
Ответ: 10 см. кв.
Формула площади ромба через диагонали
Здесь все так же просто. Нужно просто взять половину произведения диагоналей и получить площадь.
S=12⋅d1⋅d2S=frac{1}{2}cdot d_1cdot d_2
d1,d2d_1, d_2 — диагонали ромба.
Одна из диагоналей ромба равна 7 (см.), а другая в 2 раза больше первой. Найдите площадь фигуры.
Решение
d1=7d_1=7
d2=2⋅d1d_2=2cdot d_1
Найдем вторую диагональ:
d2=2⋅d1=2⋅7=14d_2=2cdot d_1=2cdot 7=14
Тогда площадь:
S=12⋅7⋅14=49S=frac{1}{2}cdot7cdot14=49 (см. кв.)
Ответ: 49 см. кв.
Формула площади ромба через две стороны и угол между ними
S=a2⋅sin(α)S=a^2cdotsin(alpha)
aa — сторона ромба;
αalpha — любой угол ромба.
Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.
Решение
a=10a=10
α=30∘alpha=30^{circ}
По формуле получаем:
S=a2⋅sin(α)=100⋅sin(30∘)=50S=a^2cdotsin(alpha)=100cdotsin(30^{circ})=50 (см. кв.)
Ответ: 50 см. кв.
Формула площади ромба по радиусу вписанной окружности и углу
S=4⋅r2sin(α)S=frac{4cdot r^2}{sin(alpha)}
rr — радиус вписанной окружности в ромб;
αalpha — любой угол ромба.
Найти площадь ромба, если угол между основаниями равен 60 градусов, а радиус вписанной окружности – 4 (см.).
Решение
r=4r=4
α=60∘alpha=60^{circ}
S=4⋅r2sin(α)=4⋅16sin(60∘)≈73.9S=frac{4cdot r^2}{sin(alpha)}=frac{4cdot 16}{sin(60^{circ})}approx73.9 (см. кв.)
Ответ: 73.9 см. кв.
Формула площади ромба по радиусу вписанной окружности и стороне
S=2⋅a⋅rS=2cdot acdot r
aa —сторона ромба;
rr — радиус вписанной окружности в ромб.
Возьмем условие из предыдущей задачи, но пусть вместо угла нам известна сторона ромба, равная 5 см.
Решение
a=5a=5
r=4r=4
S=2⋅a⋅r=2⋅5⋅4=40S=2cdot acdot r=2cdot5cdot4=40 (см. кв.)
Ответ: 40 см. кв.
Ищете того, кто сможеит помочь вам решить контрольную работу по геометрии? Наши эксперты окажут вам быструю и качественную помощь с выполнением работы!
Тест на тему “Площадь ромба”
Формулы площади ромба

$$S= ah$$
(S) — площадь ромба
(a) — сторона
(h) — высота
(a =)
(h =)

$$S= frac{1}{2} d_1 d_2$$
(S) — площадь ромба
(d_1) — диагональ
(d_2) — диагональ
(d_1=)
(d_1=)

$$S= a^2 sin alpha $$
(S) — площадь ромба
(a) — сторона
(alpha) — острый угол
(a =)
( alpha =)

$$S= frac{4r^2}{ sin alpha} $$
(S) — площадь ромба
(r) — радиус вписанной окружности
(alpha) — острый угол
(r =)
( alpha =)

$$S= 2ar $$
(S) — площадь ромба
(a) — сторона
(r) — радиус вписанной окружности
(a =)
(r =)
