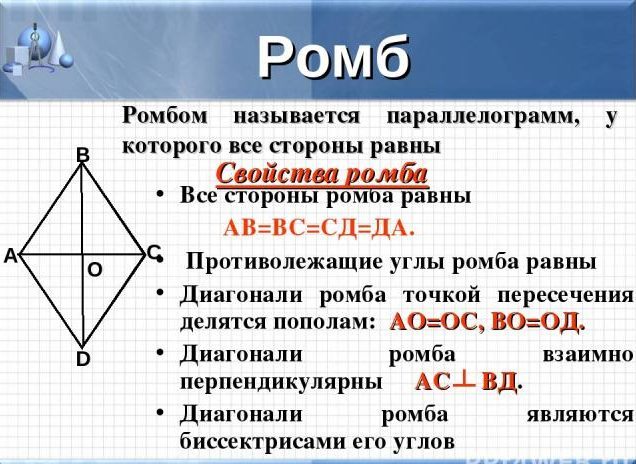
Ромб – это геометрическая фигура; параллелограмм, имеющие 4 равные стороны.
-
Формула вычисления площади
- По длине стороны и высоте
- По длине стороны и углу
-
По длинам диагоналей
- Примеры задач
Формула вычисления площади
По длине стороны и высоте
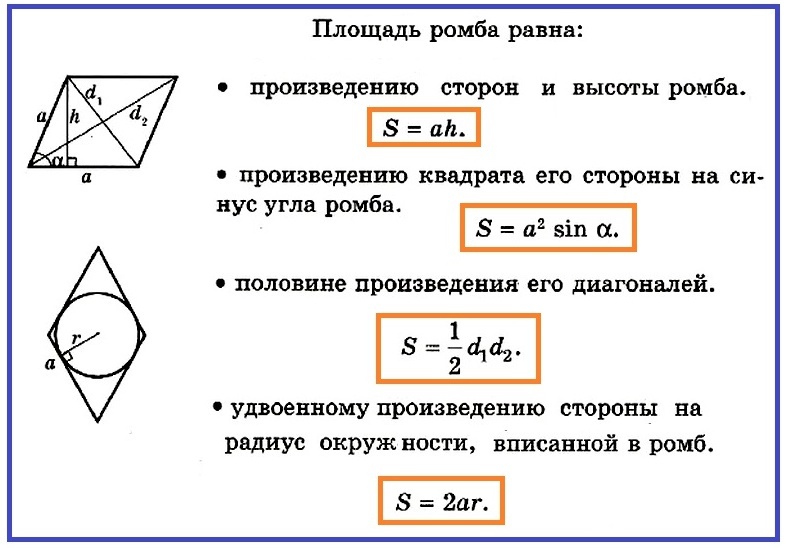
Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a ⋅ h

По длине стороны и углу
Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:
S = a 2 ⋅ sin α

По длинам диагоналей
Площадь ромба равна одной второй произведения его диагоналей.
S = 1/2 ⋅ d1 ⋅ d2

Примеры задач
Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.
Решение:
Используем первую формулу, рассмотренную выше: S = 10 см ⋅ 8 см = 80 см2.
Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.
Решение:
Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см)2 ⋅ sin 30° = 36 см2 ⋅ 1/2 = 18 см2.
Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.
Решение:
Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 ⋅ 4 см ⋅ 8 см = 16 см2.
В этой статье вы узнаете, как можно найти площадь ромба различными методами. Благодаря этим формулам будет легко решать задачи по геометрии, ведь здесь в статье будет описано, как вычислить площадь ромба, зная величину диагонали большей и меньшей, стороны, углы и диаметр вписанной окружности в ромб.
Содержание
- Как вычислить площадь ромба – свойства фигуры
- Как вычислить площадь ромба?
- Как найти площадь ромба, зная угол и сторону геометрической фигуры?
- Как вычислять площадь ромба, зная его диагонали?
- Как вычислять площадь ромба, зная его сторону и радиус вписанной в него окружности?
- Видео: Пример того, как вычислять площадь ромба
Узнать площадь ромба можно по разным формулам. Достаточно знать свойства это фигуры и свойства других фигур, ведь ромб можно разбить на треугольники, приравнять его к параллелограмму и т.п. Ниже вы увидите такие формулы. Еще необходимо знать, чем отличается ромб от четырехугольника и параллелограмма. По математическому определению. Ромб представляет собой фигуру подобную параллелограмму с равными сторонами, но в отличие от квадрата – у ромба углы не прямые. Зато сумма двух углов у основания ромба будет равняться 180 градусов. Все эти знания пригодятся для расчета площади ромба, далее подробнее.
Как вычислить площадь ромба – свойства фигуры
Прежде, чем вычислить площадь ромба, лучше ознакомиться со свойствами данной фигуры. Ведь благодаря знанию этих характеристик дальше проще будет доказать вероятность той или иной формулы. Ранее упоминалось уже, что такое ромб. Он представляет собой фигуру с равными абсолютно всеми сторонами, равными противоположными острыми и тупыми углами, но не прямыми.
Ромб имеет следующие свойства:
- у него все стороны между собой равны
- углы, лежащие напротив друг друга, тоже равны
- диагонали данной фигуры являются биссектрисами, в точке пересечения делятся на равные отрезки
- также диагонали пересекаются в центре ромба и под прямыми углами
- противоположные стороны фигуры не могут пересекаться, даже если продлить лучи они же параллельны, как у параллелограмма.
ВАЖНО: Обратите внимание, что ромб можно разбить на четыре прямоугольных треугольника, которые будут между собой равны по площади, или на два равносторонних идентичных треугольника, см. изображение выше.
Как вычислить площадь ромба?
Итак, давайте выясним, как вычисляется площадь ромба. Давайте воспользуемся для этого формулой площади прямоугольника, где:
- S = a • b, где a, b – стороны прямоугольника.
Чтобы было понятно, как вывести из этой формулы, формулу площади ромба, смотрите объяснение:
- Нарисуйте ромб, проведите высоту к основанию ромба BH.
- Из точки D на линию AD проведите тоже высоту CH1.
- Выходит что треугольник ABH и треугольник CH1D между собой равны по двум общим сторонам, ∠ углу между ними.
- Значит AH=DH1. Площадь образовавшегося квадрата будет равна площади ромба
- А значит BH • HH1 – это и есть площадь ромба, другими словами произведение высоты BH ромба на сторону AD и будет S площадью ромба, поскольку HH1 = BC, а BH – это высота.
Из доказательства вытекает, что:
- S ромба = a • h и измеряется в квадратных единицах.
Как найти площадь ромба, зная угол и сторону геометрической фигуры?
Теперь мы знаем, как выглядит формула площади ромба, можем по этой же формуле найти и S площадь ромба, зная чему равна сторона ромба и ∠ угол, например, острый у основания, как на фото ниже.
- S = a • h
Но в нашем случае нам неизвестна высота ромба, ее следует найти. Для этого придется рассмотреть треугольник прямоугольный, который получился, когда была проведена высота к основанию ромба.
В этом треугольнике известна гипотенуза и ∠α. Чтобы вычислить площадь всей фигуры, понадобится найти высоту. А h = a • sin∠α. Значит S площадь равностороннего параллелограмма (ромба) равняется:
- S = a • a • sin∠α = a² • sin∠α
Как вычислять площадь ромба, зная его диагонали?
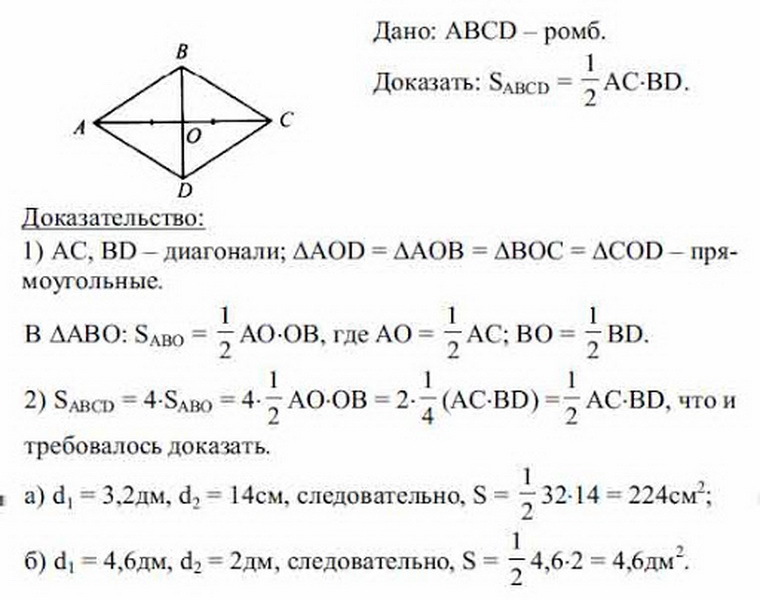
Чтобы узнать формулу площади ромба, когда известны только (a, b) диагонали, следует рассмотреть следующий пример. Дано BCDA – ромб и знаем чему равны диагонали. Теперь следует найти S площадь равностороннего параллелограмма по величинам диагоналей.
Ранее уже рассматривали свойства ромба. Диагонали ромба равны, в точке пересечения делятся на равные отрезки. Из этого следует, что все треугольники, которые вписаны в фигуру в результате пересечения обеих диагоналей тоже равны между собой и они прямоугольные (по трем сторонам). Чтобы найти площадь ромба, достаточно найти площадь одного треугольника и полученные данные умножить на 4.
Итого выходит, что:
- S ромба = 4 (1/2 AO • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) = 4 • 1/8 AC • BD = 1/2 BD • AC, итого площадь S ромба будет = произведению a • b (диагоналей) деленное на два: S = 1/2 a • b
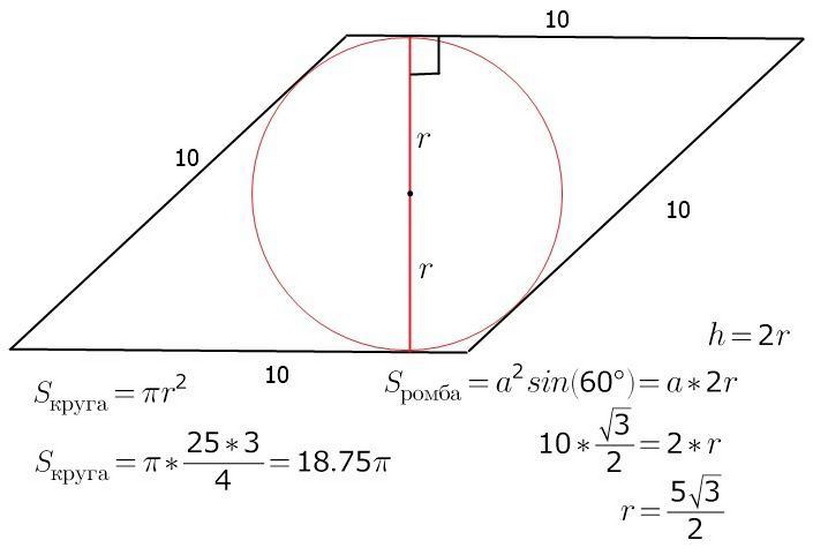
Как вычислять площадь ромба, зная его сторону и радиус вписанной в него окружности?
Площадь ромба можно рассчитать, зная r – радиус и a – длину стороны фигуры. Уже известно, что S – площадь фигуры будет равна произведению b – стороны на h – высоту. Через центр окружности, он же будет являться и центром пересечения a, b – диагоналей ромба. Проведите высоту и одновременно диаметр ромба. На изображении видно, что высота фигуры – это два радиуса окружности. Теперь легко будет найти и площадь самого ромба:
- S = a • h = a • 2r
Ниже смотрите пример задачи на данную тематику.
Еще смотрите подобные статьи на данную тематику здесь:
- Площадь прямоугольника, как найти?
- Как найти площадь круга?
- Площадь квадрата – формулы.
Видео: Пример того, как вычислять площадь ромба
В статье рассмотрим формулу площади ромба и не одну! На картинках покажем, как легко находиться площадь ромба по простым формулам.
Существует большое количество заданий на нахождение той или иной величины в ромбе и в этом нам помогут формулы, о которых и пойдет речь.
Ромб относится к отдельному виду четырехугольников, так как у него все стороны равны. Так же представляет частный случай параллелограмма в котором стороны АВ=ВС=СD=АD равны.
Заметка: Если Вам нужна курсовая, контрольная или дипломная работа, тогда вам на webmath.ru. или просто перейдите по ссылке заказать курсовую работу (http://www.webmath.ru/zakaz_kursovye.php).
Ромб обладает следующими свойствами:
– у ромба параллельные углы равные,
– сложение двух соседних углов равно 180 градусам,
– Пересечение диагоналей под углом в 90 градусов,
– Биссектрисами ромба, приходятся его же диагонали,
– Диагональ при пересечении делится на равные части.
Ромб обладает следующими признаками:
– Если у параллелограмма в котором диагонали встречаются под углом 90 градусов, то он называется ромбом.
– Если у параллелограмма в котором биссектриса это диагональ, то он называется ромбом.
– Если у параллелограмма равные стороны – это ромб.
– Если у четырехугольника равные стороны – это ромб.
– Если у четырехугольника в котором биссектриса это диагональ и диагонали встречаются под углом 90 градусов, то это ромб.
– Если у параллелограмма одинаковые высоты – это ромб.
Из вышеперечисленных признаков можно сделать вывод, что они нужны для того чтобы научиться отделять ромб от других схожих с ним фигур.
Так как в ромбе все стороны одинаковы периметр находится по следующей формуле:
Р=4а
Площадь ромба формула
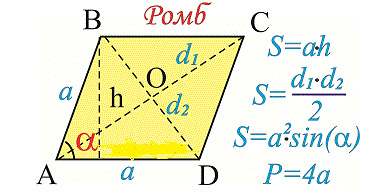
Данных формул несколько. Самая простая решается как сложение площадь 2 треугольников, которые получились в результате деления диагоналей.
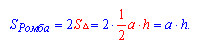
С помощью второй формулы можно решать задачи с известными диагоналями ромба. В этом случае площадью ромба будет: сумма диагоналей деленная на два.
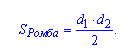
Очень просто в решении и не забудется.
Третью формулу можно использовать когда знаешь угол между сторон. Зная его можно найти площадь ромба, она будет равна квадрату сторон на синус угла. При чем нет разницы какой угол. так как синус угла имеет единое значение.
Важно помнить что измерение площади происходит в квадратах, а периметра в единицах. Данные формулы очень легко применяются на практике.
Так же могут встретиться задачи на поиск радиуса по вписанной в ромб окружности.
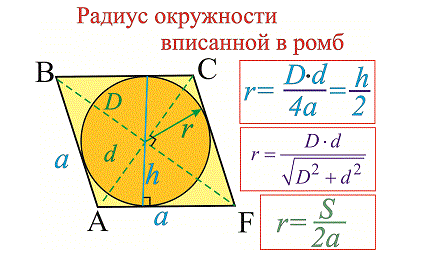
Для этого так же существует несколько формул:
В помощью первой формулы радиус находится как произведение диагоналей поделенное на число полученное от сложения всех сторон. либо равняется половине высоты ( r=h/2).
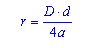
Во второй формуле взят принцип из первой, применяется мы знаем диагонали и стороны ромба.
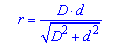
В третьей формуле радиус выходит из высоты меньшего из треугольников, получившегося в результате пересечения.
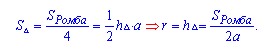
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Ромб — это параллелограмм, в котором все стороны равны друг другу.
Онлайн-калькулятор площади ромба
Если стороны ромба образуют прямой угол, то получим квадрат.
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.
Площадь ромба, как и площади большинства геометрических фигур, можно найти несколькими способами. Разберемся в их сути и рассмотрим примеры решений.
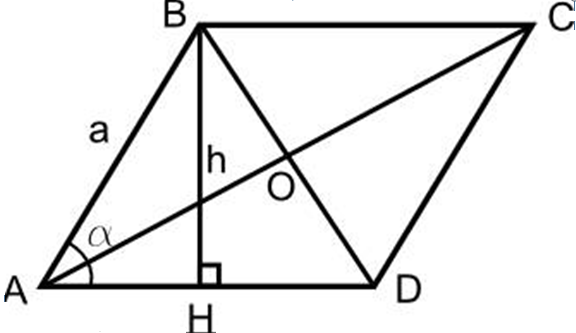
Формула площади ромба по стороне и высоте
Пусть нам дан ромб со стороной aa и высотой hh, проведенной к этой стороне. Так как ромб это параллелограмм, то его площадь мы находим так же, как и площадь параллелограмма.
S=a⋅hS=acdot h
aa — сторона;
hh — высота, опущенная на сторону aa.
Решим простой пример.
Сторона ромба равна 5 (см.). Высота, опущенная к этой стороне, имеет длину 2 (см.). Найти площадь ромба SS.
Решение
a=5a=5
h=2h=2
Пользуемся нашей формулой и вычисляем:
S=a⋅h=5⋅2=10S=acdot h=5cdot 2=10 (см. кв.)
Ответ: 10 см. кв.
Формула площади ромба через диагонали
Здесь все так же просто. Нужно просто взять половину произведения диагоналей и получить площадь.
S=12⋅d1⋅d2S=frac{1}{2}cdot d_1cdot d_2
d1,d2d_1, d_2 — диагонали ромба.
Одна из диагоналей ромба равна 7 (см.), а другая в 2 раза больше первой. Найдите площадь фигуры.
Решение
d1=7d_1=7
d2=2⋅d1d_2=2cdot d_1
Найдем вторую диагональ:
d2=2⋅d1=2⋅7=14d_2=2cdot d_1=2cdot 7=14
Тогда площадь:
S=12⋅7⋅14=49S=frac{1}{2}cdot7cdot14=49 (см. кв.)
Ответ: 49 см. кв.
Формула площади ромба через две стороны и угол между ними
S=a2⋅sin(α)S=a^2cdotsin(alpha)
aa — сторона ромба;
αalpha — любой угол ромба.
Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.
Решение
a=10a=10
α=30∘alpha=30^{circ}
По формуле получаем:
S=a2⋅sin(α)=100⋅sin(30∘)=50S=a^2cdotsin(alpha)=100cdotsin(30^{circ})=50 (см. кв.)
Ответ: 50 см. кв.
Формула площади ромба по радиусу вписанной окружности и углу
S=4⋅r2sin(α)S=frac{4cdot r^2}{sin(alpha)}
rr — радиус вписанной окружности в ромб;
αalpha — любой угол ромба.
Найти площадь ромба, если угол между основаниями равен 60 градусов, а радиус вписанной окружности – 4 (см.).
Решение
r=4r=4
α=60∘alpha=60^{circ}
S=4⋅r2sin(α)=4⋅16sin(60∘)≈73.9S=frac{4cdot r^2}{sin(alpha)}=frac{4cdot 16}{sin(60^{circ})}approx73.9 (см. кв.)
Ответ: 73.9 см. кв.
Формула площади ромба по радиусу вписанной окружности и стороне
S=2⋅a⋅rS=2cdot acdot r
aa —сторона ромба;
rr — радиус вписанной окружности в ромб.
Возьмем условие из предыдущей задачи, но пусть вместо угла нам известна сторона ромба, равная 5 см.
Решение
a=5a=5
r=4r=4
S=2⋅a⋅r=2⋅5⋅4=40S=2cdot acdot r=2cdot5cdot4=40 (см. кв.)
Ответ: 40 см. кв.
Ищете того, кто сможеит помочь вам решить контрольную работу по геометрии? Наши эксперты окажут вам быструю и качественную помощь с выполнением работы!
Тест на тему “Площадь ромба”
Download Article
Download Article
A rhombus is a parallelogram with four congruent sides. It does not have to have right angles.[1]
There are three formulas for finding the area of a rhombus. Just follow these steps if you want to know how to do it.
-

1
Find the length of each diagonal. The diagonals of a rhombus are the lines that connect the opposite vertices (corners) in the center of the shape. The diagonals of a rhombus are perpendicular and form four right triangles through their intersection.[2]
- Let’s say the diagonals are 6 cm. and 8 cm. long.
-

2
Multiply the length of the diagonals. Just write down the length of the diagonals and multiply them. In this case, 6 cm x 8 cm = 48 cm2. Don’t forget to square the units since you’re working in square units.[3]
Advertisement
-

3
Divide the result by 2. Since 6 cm x 8 cm = 48 cm2, just divide the result by 2. 48 cm2/2 = 24 cm2. The area of the rhombus is 24 cm2.[4]
Advertisement
-

1
Find the base and the height.[5]
You can also think of this as multiplying the altitude of the rhombus with the length of the side of the rhombus. Let’s say the height of the rhombus is 7 cm and the base is 10 cm. -

2
Multiply the base and height. Once you know the base and height of the rhombus, all you have to do to find the area of the shape is to multiply them. So, 10 cm x 7 cm = 70 cm2. The area of the rhombus is 70 cm2.[6]
Advertisement
-

1
Square the length of any side. A rhombus has four equal sides, so it doesn’t matter which side you choose. Let’s say the side is 2 cm long. 2 cm x 2 cm = 4 cm2.[7]
-

2
Multiply it by the sine of one of the angles. It doesn’t matter which angle you choose. Let’s say one of the angles is 33 degrees. Just multiply sine (33) by 4 cm2 to get the area of the rhombus. (2 cm)2 x sine (33) = 4 cm2 x 0.55 = 2.2 cm2. The area of the rhombus is 2.2 cm2.[8]
Advertisement
Rhombus Area Calculator, Practice Problems, and Answers
Add New Question
-
Question
How do I find the perimeter of a rhombus?

Perimeter = sum of all sides. The rhombus has equal sides, so its perimeter = side x 4.
-
Question
How can I find the height of a rhombus?

In a rhombus, the diagonals bisect and are perpendicular, meaning that inside the rhombus there are four right-angle triangles, with side lengths half that of the diagonals, use the pythagoran theorem to find the hypotenuses a² + b² = c²
Now we have the base, given any of the angles inside the rhombus, we can find all of them because they are corresponding and all add up to 360 degrees, once we have all of the angles, another two identical triangles appear. we only have to use one of these as they are identical.
Now we have the hypotenuse and an angle of this triangle so using trigonometry we can find the adjacent side which is the height of the rhombus.
-
Question
How do I determine the perimeter given one diagonal and the area?

Use the Pythagorean theorem to find the sides and then find the perimeter.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
A rhombus is a shape with four equal sides, each of which is parallel to the opposite side. While a square is a type of rhombus, they can also be diamond-shaped, with angles of greater or less than 90° at each corner. There are several easy ways to find the area of a diamond-shaped rhombus. One is to measure the rhombus diagonally from corner to corner, each way. For instance, let’s say your rhombus measures 10 cm across lengthwise and 6 cm across widthwise. Once you find the length of each diagonal, multiply the lengths together. In this case, 10 cm x 6 cm = 60 cm. Finally, divide the result by 2. Don’t forget to square your units when you write the result, since you’re measuring the area. 60/2 = 30, so our rhombus has an area of 30 cm squared. Another simple method is to multiply the base length of the rhombus by its height. Measure the width of the bottom line of the rhombus, then take a perpendicular measurement from the base to the opposite line at the top. Multiply the measurements together to find the area. For instance, if a rhombus is 12 cm long at the base and has a height of 8 cm, the area of the rhombus would be 96 cm squared. If you only know the length of one side of the rhombus and one of the angles, you can still figure out the area using trigonometry. To do this, square the length of the known side, then multiply the result by the sine of one of the angles. For instance, if the rhombus has one side with a length of 6 cm, and you know it contains a 45° angle, the area would be 36 cm squared x sin(45°), or approximately 30.63 cm squared. If you want to learn how to use trigonometry to find the area of the rhombus, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 892,161 times.
