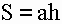Площадь ромба по периметру
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Ромб представляет собой параллелограмм, все стороны которого одинаковы по длине, а углы, в отличие от квадрата и прямоугольника, не эквивалентны $90°$.
Рисунок 1. Ромб. Автор24 — интернет-биржа студенческих работ
Для того чтобы найти площадь этого геометрического объекта, необходимо применить одну из формул:
$S=frac{AC cdot BD}{2}left(1right)$, здесь $AC$ и $BD$ — диагонали;
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
$S=AB cdot H_{AB}left(2right)$, здесь $AB$ — сторона, а $H_{AB}$ —длина высоты, опущенной с неё;
$S=AB^2 cdot sin αleft(3right)$.
Так как периметр ромба $P=AB^2$, равенство $(3)$ можно переписать через периметр:
$S=P cdot sin αleft(3right)$.
Пример 1
Нужно выяснить, является ли четырёхугольник-параллелограмм, диагонали которого перпендикулярны, ромбом (смотрите рис.1).
Решение:
Рассмотрим $4$-угольник $ABCD$ с перпендикулярными диагоналями, пересекающимися в точке $O$.
- $triangle AOD$ и $triangle AOB$ являются равными так как они имеют общую сторону $OA$, а все углы, образуемые пересечением диагоналей — прямые, то есть равны. Также равны между собой $OB$ и $OD$ по свойству параллелограмма.
- Из предыдущего пункта следует, что $AB=AD$. Также можно вспомнить, что одно из свойств параллелограмма — это равенство его противоположных сторон, следовательно, $AB=AD=CD=CB$. Все стороны данного $4$-угольника равны, а это значит, что он является ромбическим.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 22.04.2023
|
У ромба все стороны равны, значит длинна стороны равна а=Р/4, потом при помощи тригонометрии находим большую и малую диагональ. d1=2a*sin(b) d2=2a*cos(b) Площадь определяется по формуле S=(2a*sin(b)*2a*cos(b))/2=2*a^2*sin(b)*cos(b) – это длнный вариант Второй вариант есть прямо на рисунке система выбрала этот ответ лучшим bezdelnik 5 лет назад Площадь ромба по стороне a и острому углу α находим по формуле : S = a^2*Sin α. Сторона а =Р/4, где Р – периметр ромба. Тогда S = Р^2*Sin α /16. Например, при Р=40 см и α = 30° S = 1600*0,5 /16 = 50 квадратных см. Знаете ответ? |
Содержание:
- Формулы площади ромба:
- Формула периметра ромба:
Ромб – это четырёхугольник, у которого все стороны равны.
Ромб можно рассматривать как частный случай параллелограмма, у которого или две смежные стороны равны, или диагонали
взаимно перпендикулярны, или диагональ делит угол пополам. Ромб с прямыми углами называется квадратом.
Формулы площади ромба:
Площадь геометрической фигуры – часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади ромба выражается числом заключающихся в него квадратных единиц.
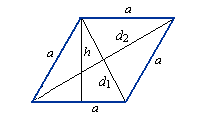
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
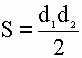
S – площадь ромба
a – длина основания ромба
h – длина высоты ромба
d1 – длина 1-ой диагонали
d2 – длина 2-ой диагонали
См. также: Программа для расчета площади ромба.
Формула периметра ромба:
Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.
1) Периметр ромба равен сумме 4-х длин его сторон или произведению
длины любой его стороны на четыре (так как у ромба длины всех сторон равны).
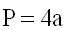
P – периметр ромба
a – длина стороны ромба
Остались вопросы?
Здесь вы найдете ответы.
Что понимается под высотой ромба?
Высота ромба представляет собой перпендикуляр, который опущен из одного из
его углов на сторону, противоположную данному углу.
Высота ромба, опущенная из одного его угла, делит противолежащую сторону
пополам. Как найти величины углов этого ромба?
Обозначим имеющийся ромб как ABCD. Из его угла В проведем высоту ВН, после
чего получим треугольник АВН с прямым углом. Известно, что длина всех
сторон ромба одинаковая, а длина АН равна половине длины АВ. Зная это и
используя теорему, которая является обратной теореме о 30-градусном угле,
можно провести доказательство того, что угол АВН равен 30 градусам.
Учитывая то, что сумма всех углов треугольника равна 180 градусом, можно
найти неизвестную величину третьего угла треугольника:
BAH=180-30-90=60 градусов.
Так, угол АВС равен:
ABC=180-60=120 градусов.
Как найти высоту ромба, если единственной величиной, которая известна,
является длина одной его стороны?
Известна формула площади (S) ромба, которая представляет собой
произведение длины его стороны (а) на высоту (h), проведенную к ней:
S = a*h.
Есть возможность выразить высоту из приведенной выше формулы. Она будет
равна отношению площади ромба к длине его стороны:
h = S/a.
Имеется треугольник с прямым углом и катетами длиной 3 см. и 4 см. Его
площадь аналогична площади ромба со стороной 5 см. Как найти высоту ромба?
Площадь (S) треугольника с прямым углом рассчитывается путем деления
пополам произведения длин его катетов. В данном случае она будет равна:
SΔ = 4*3/2 = 6 см.кв.
Площадь ромба определяется умножением длины его стороны на высоту,
проведенную к ней. Если принять высоту за х, и учесть, что площадь ромба
равна площади прямоугольного треугольника (6 см.кв.), то:
S = 5*x = 6 см.кв.
Отсюда можно найти значение х:
х = 6/5 = 1,2 см.
Ответ: высота ромба составляет 1,2 см.
Как найти высоту ромба при условии, что длины его диагоналей равны 6 см. и 8
см.?
Диагонали, проведенные в ромбе, делят эту фигуру на четыре треугольника,
которые являются равными. Длины катетов этих треугольников составляют 3
см. и 4 см. Такой вывод можно сделать на основании того, что в точке
пересечения диагоналей они делятся пополам. Гипотенуза (с) треугольников
представляет собой сторону ромба. Ее длина равна:
с = √(9+16) = √25 = 5 см.
Следовательно, сторона ромба также равна 5 см.
Площадь ромба высчитывается как произведение длин его диагоналей, деленное
пополам:
S = d1*d2/2 = 6*8/2 = 24 см. кв.
Известна также другая формула, используемая для вычисления площади ромба,
в которой длина его стороны (а) умножается на высоту(h):
S = a*h
Из данной формулы выражаем высоту:
h = S/a = 24/5 = 4,8 см.
Ответ: Высота ромба составляет 4,8 см.
Как найти высоту ромба при условии, что его диагонали равны d1 и d2, а длина
стороны – а?
Высоту ромба можно рассчитать, если его диагонали (d1 и d2)и сторона (а) –
известные величинами. В этом случае для определения неизвестной высоты
следует пользоваться приведенной ниже формулой:
h = (d1 * d2)/a
Площадь ромба составляет 60 см.кв., а его периметр равен 48 см. Как найти
высоту ромба в конкретном случае?
Периметр (Р) ромба равен сумме длин всех его сторон (а) и вычисляется по
следующей формуле:
Р = а+а+а+а
В данном случае периметр ромба равен 48 см., это значит, что:
а+а+а+а = 48 см.
Находим значение а:
а = 48/4 = 12 см.
Площадь ромба (S) является произведением длины его стороны (а) и высоты
(h), проведенной к этой стороне:
S = а*h
В задании сказано, что площадь ромба – 60 см.кв. Значит:
а*h=60
Находим неизвестную высоту:
h=60/а=60/12=5 см.
Ответ: Высота ромба – 5 см.
Как найти высоту ромба, зная о том, что его площадь составляет 48 см.кв., а
периметр – 32 см.?
Согласно формуле расчета периметра (Р) ромба, он равен сумме длин всех его
сторон (а) (Р=а+а+а+а). Известно, что все стороны ромба имеет одинаковую
длину. Из этого следует, что длина одной стороны будет равна ¼ части его
периметра:
а = Р/4 = 32/4 = 8 см.
Площадь (S) ромба можно высчитать путем умножения длины его стороны (а) на
высоту (h), проведенную к ней:
S = а* h
В конкретном случае:
48 = 8* h
Отсюда можем найти высоту (h), разделив площадь на длину стороны ромба:
H = 48/8 = 6 см.
Ответ: Высота ромба составляет 6 см.
Отношение длин диагоналей ромба выглядит как 10/24. Его периметр равен 52
см. Как найти высоту ромба в данном случае?
Периметр (Р) ромба равен сумме длин всех его сторон (а), длины которых
равны. Это значит:
Р = 4*а
По условию задачи:
52 = 4*а
Следовательно:
а = 52/13 = 13 см.
Предположим, что длина одной из диагоналей ромба равна 10х, тогда длина
второй его диагонали будет выглядеть как 24х. Отношение их длин можно
записать в следующем виде:
10х:24х=10:24
Доказано, что диагонали ромба взаимно перпендикулярны и в точке
пересечения они делятся пополам, при этом образуя четыре равных
треугольника с прямым углом.
Теорема Пифагора гласит, что сумма длин его катетов, возведенных во вторую
степень, равна длине гипотенузы, которая также возведена в квадрат:
с2 = а2 + b2
Для данной задачи это равенство записывается так:
(5х)²+(12х)²=13²
Отсюда видно, что:
169х²=169; следовательно, х2 = 1. Значит х тоже будет равен 1.
Длина диаметра, обозначенного как 10х, равна 10 см. (10*1), а длина
второго диаметра, который обозначен как 24х, равна 24 см. (24*1).
Площадь (S) ромба рассчитывается как:
S = d₁*d₂/2 или a·h
Из этого можно составить следующее уравнение:
d₁*d₂=2a*h
Выражаем h и получаем:
h= d₁*d₂/2*а=10·24:26=240/26=120/13 см.
Какая формула используется с целью вычисления высоты ромба?
Ромб имеет четыре высоты. Все они имеют равные длины. Вывод об этом можно
сделать, рассмотрев все треугольные фигуры, элементами которых являются
эти высоты. Есть возожность высчитать высоту ромба при помощи различных
параметров, которые могут быть указаны в условии конкретной задачи.
Предположим, что нам известна площадь (S) ромба и длина его стороны (а). В
этом случае высота ромба будет равна отношению его площади к длине высоты:
h = S/a.
Если же по условию задачи известны длины диагоналей ромба d1 и d2, а также
его сторона а, то высоту можно рассчитать так: h = (d1*d2 )/a.
В случае, когда известна длина стороны (а) ромба и угол А, находящийся
между смежными сторонами, то для расчета высоты ромба используется
следующая формула:
h = a*a*sin A /a = a*sin A.
Существуют также и другие варианты вычисления длины высоты ромба на
основании того, какие величины будут известны по условию задания. Однако
ключевыми параметрами, используя которые можно вычислить высоту ромба,
являются диагонали, длина любой его стороны и угол, образованный между
смежными сторонами.
В каком виде записываются формулы, используемые для определения площади
ромба?
Площадь ромба можно рассчитать одним из трех способов:
1. S = a² sin a, в которой α — образованный двумя сторонами угол, a —
сторона.
2. S = ah, или Длина стороны ромба, умноженная на его высоту.
3. S = (d1*d2)/2, в которой d1 и d2 – длины диагоналей фигуры.
На сторону ромба опущена высота, которая на 1,7 см. меньше ее длины.
Периметр фигуры составляет 32 см. Как в данном случае вычислить площадь
ромба?
Зная, чему равен периметр ромба, можно вычислить длину его стороны:
Р/4 = 8 см.
Известно, что высота данной фигуры меньше ее стороны на 1,7 см. Теперь
можем определить длину высоты:
h = 8-1,7 = 6,3 см.
Площадь ромба можно найти, умножив его сторону на высоту, которая на нее
опущена:
8 * 6,3 = 50,4 см².кв.
Ответ: S = 50,4 см. кв.
Известно, что диагонали ромба относятся как 4/3, а его сторона составляет 10
см. Как найти площадь ромба?
Если длины диагоналей фигуры относятся как 4/3, то их половины будут
относиться также:
(4d)²+(3d)²=10² = 16d²+9d² = 100
Отсюда:
25d²=100
d =2,
Значит:
d¹/2 = 4d = 8 см.
d²/2 = 3d = 6 см.
Теперь можно найти площадь:
S= 2*d¹/2*d²/2=2*8*6 = 96 см.кв.
Ответ: S ромба = 96 см.кв.
Как записывается формула расчета площади ромба через длины его диагоналей d1
и d2?
Площадь ромба можно описать как сумму площадей 2-х треугольных фигур,
основанием которых является одна диагональ, а вторая диагональ ромба
представляет собой сумму длин высот этих фигур. Диагонали ромба при
пересечении образуют угол в 90 градусов. На основании этого можно найти
площадь ромба следующим образом:
S = ½ d1*d2.
Как записать формулу вычисления площади ромба через диагонали?
Известно, что, пересекаясь, диагонали ромба образуют угол в 90 градусов и
в точке пересечения делятся пополам.
Для расчета площади ромба через диагонали нужно перемножить их длины, а
затем разделить полученное число на два:
S = ½ d1*d2.
Для примера можно рассмотреть ромб, одна диагональ которого равна 5 см., а
вторая – 4 см. Тогда его площадь будет равна:
S=1/2*5*4=10 см. кв.
Как выглядит формула для определения площади ромба?
S ромба возможно вычислить, перемножив длину одной из его сторон (а) и
высоту (h). Формула записывается так:
S=a*h.
См. также: Программа для расчета периметра ромба.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Ромб. Формулы, признаки и свойства ромба
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
AC 2 + BD 2 = 4AB 2
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 1 = a √ 2 – 2 · cosβ
d 2 = a √ 2 + 2 · cosβ
d 2 = a √ 2 – 2 · cosα
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Площадь ромба – формула, пример расчет, как начертить
Через диагонали
Диагональ ромба d1
Диагональ ромба d2
Результат
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Свойства ромба
На рисунке выше ( ABCD ) – ромб, ( AC = DB = CD = AD ) . Так как ромб – это параллелограмм, то он обладает всеми свойствами параллелограмма, но так же есть свойства присущие только ромбу.
В любой ромб можно вписать окружность. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей. Радиус окружности равен половине высоты ромба:
Формула вычисления площади
1. По длине стороны и высоте:
Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a*h
2. По длине стороны и углу
Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:
S = a 2 *sin α
3. По длинам диагоналей
Площадь ромба равна одной второй произведения его диагоналей.
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
AC 2 + BD 2 = 4AB 2
Примеры задач
Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.
Решение:
Используем первую формулу, рассмотренную выше: S = 10 см * 8 см = 80 см 2 .
Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.
Решение:
Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см) 2 * sin 30° = 36 см 2 * 1/2 = 18 см 2 .
Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.
Решение:
Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 * 4 см * 8 см = 16 см 2 .
Через основание и высоту
Высоты ромба h
Сторона ромба а
Площади фигур
Расчет площади квадрата, прямоугольника, параллелограмма, треугольника, трапеции, ромба, круга (площадь фигур).
Площади фигур
Площадь ромба по углу и противолежащей диагонали
Площадь ромба по углу и диагонали проведенной из этого угла
Способ расчета площади ромба
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: 
где a – стороны, h – высота
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: 
где d1, d2 – диагонали
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: 
где a – сторона, α – угол между сторонами
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: 
где r – радиус вписанной окружности, α – угол между сторонами
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: 
где r – радиус вписанной окружности, a – сторона
Формула площади ромба через две стороны и угол между ними
a — сторона ромба;
— любой угол ромба.
Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.
Решение
По формуле получаем:
S = a 2 ⋅ sin ( α ) = 1 0 0 ⋅ sin ( 3 0 ∘ ) = 5 0 (см. кв.)
Ответ: 50 см. кв.
Формула площади ромба через угол и радиус вписанной окружности
Формула площади ромба через сторону и угол
Таблица с формулами площади ромба
В зависимости от известных исходных данных, площадь ромба можно вычислить по различным формулам.
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула |
| 1 | сторона и высота |  |
| 2 | диагонали |  |
| 3 | диагональ и угол между сторонами |  |
| 4 | диагональ и угол между сторонами |  |
| 5 | сторона и угол между сторонами |  |
| 6 | радиус вписанной окружности и угол между сторонами |  |
| 7 | сторона и радиус вписанной окружности |  |
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d56470b5ce02de4 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
[spoiler title=”источники:”]
http://exceltut.ru/ploshhad-romba-formula-primer-raschet-kak-nachertit/
http://mathvox.ru/geometria/mnogougolniki/glava-6-romb-i-ego-svoistva/ploschad-romba-i-vpisannaya-okrujnost-formula-1/
[/spoiler]
Ромб – это геометрическая фигура; параллелограмм, имеющие 4 равные стороны.
-
Формула вычисления площади
- По длине стороны и высоте
- По длине стороны и углу
- По длинам диагоналей
- Примеры задач
Формула вычисления площади
По длине стороны и высоте
Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a ⋅ h
По длине стороны и углу
Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:
S = a 2 ⋅ sin α
По длинам диагоналей
Площадь ромба равна одной второй произведения его диагоналей.
S = 1/2 ⋅ d1 ⋅ d2
Примеры задач
Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.
Решение:
Используем первую формулу, рассмотренную выше: S = 10 см ⋅ 8 см = 80 см2.
Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.
Решение:
Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см)2 ⋅ sin 30° = 36 см2 ⋅ 1/2 = 18 см2.
Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.
Решение:
Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 ⋅ 4 см ⋅ 8 см = 16 см2.