Каталог заданий.
Ромб
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 18 № 311333 

i
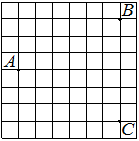
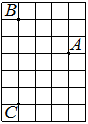
На рисунке изображен ромб ABCD. Используя рисунок, найдите
Аналоги к заданию № 311333: 311376 Все
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 2)
Решение
·
Помощь
2
Тип 18 № 311376 

i
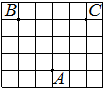
На рисунке изображен ромб ABCD. Используя рисунок, найдите
Аналоги к заданию № 311333: 311376 Все
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.6)
Решение
·
Помощь
3
Тип 18 № 348446 

i
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Аналоги к заданию № 348446: 348586 349027 349478 … Все
Решение
·
Помощь
4
Тип 18 № 356974 

i
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Аналоги к заданию № 356974: 356975 356976 356977 … Все
Источник: Банк заданий ФИПИ
Решение
·
Помощь
Пройти тестирование по этим заданиям
Всем привет!
До ОГЭ по математике осталось совсем немного времени, но с другой стороны его не так уж и мало, чтобы успеть подготовиться и получить хороший результат на экзамене!
С этой статье мы разберем, как решать одно из самых простых заданий по математике, а именно №18. Кроме того, это задание относится к блоку “Геометрия”, а для того, чтобы успешно сдать ОГЭ, необходимо набрать как минимум два балла по геометрии! И спомощью этого задания вы уже получите как минимум один балл))
Даже если вам тяжело дается геометрия, это задание сможет решить каждый школьник..нужно просто повторить немного теории и научиться пользоваться некоторыми формулами, которые будут вам доступны на экзамене в форме справочных материалов.
В качестве примеров я взяла 5 заданий из сборника Ященко для подготовке к ОГЭ 2023. Итак, поехали.
Задание 1
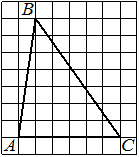
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до отрезка BC.
Здесь все просто – расстояние от точки до прямой – это перпендикуляр, проведенный к этой прямой. Поэтому соединяем точки В и С в отрезок ВС, проводим к нему перпендикуляр из точки А. Считаем длину его по клеточкам:
Задание 2
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Для того, чтобы найти площадь трапеции, необходимо вспомнить формулу нахождения площади. Но на экзамене выдаются справочные материалы, поэтому найти эту формулу не составит никакого труда:
Осталось расшифровать эту формулу:
a и b – это основания трапеции, h -высота трапеции. Дальше считаем все по клеточкам и подставляем полученные значения в формулу:
Задание 3
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Здесь, как и в предыдущем задании, мы можем воспользоваться справочными материалами и найти формулу площади треугольника.
В этом задании используем 1 формулу, где а – это основание треугольника, h – высота, проведенная к основанию. В качестве основания мы берем сторону, расположенную слева, так как ее можно посчитать точно по клеточкам, соответственно и высоту проводим к этой стороне. Далее считаем клетки, подставляем в формулу и вычисляем площадь.
Задание 4
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. … Найдите длину его средней линии, параллельной стороне AC.
Для решения этой задачи необходимо знать формулу нахождения средней линии. Но и здесь нам помогут справочные материалы. Там эта формула конечно же есть, даже если вы впервые слышите о таком понятии, как средняя линия, здесь все предельно ясно: нужно нижнее основание треугольника разделить на 2.
Остается только посчитать длину нижнего основания по клеточкам и разделить полученное значение на два.
Задание 5
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.
Находим формулу площади ромба в справочных материалах:
Далее считаем диагонали ромба по клеточкам, подставляем полученные значения в формулу площади и вычисляем площадь ромба:
Видеоразбор других прототипов 18 задания можно посмотреть здесь:
Подписывайтесь на канал, чтобы успешно подготовиться к ОГЭ 2023!
Если статья была полезна, не забудьте поставить лайк, это очень поможет ее продвижению!
Пишите в комментариях, какие еще задания ОГЭ подробно разобрать?
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.
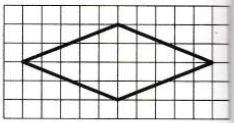
Источник: ОГЭ Ященко 2022 (36 вар)
Решение:
Площадь ромба находится по формуле, через диагонали:
S=frac{1}{2}cdot d_{1}cdot d_{2}=frac{1}{2}cdot 4cdot 10=2cdot 10=20
Ответ: 20.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.6 / 5. Количество оценок: 41
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Задание 3. ЕГЭ. Найти площадь ромба
Рубрика Задание 3, Решаем ЕГЭ по математике Комментарии (0)
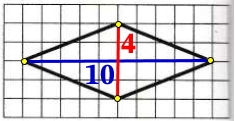
Задание. На клетчатой бумаге с размером клетки 1 × 1 изображен ромб. Найдите его площадь.

Решение:

Площадь ромба равна половине произведения его диагоналей, т. е.
![]()
По рисунку находим: AC = 10, BD = 2, тогда
![]()
Ответ: 10
Понравилось? Нажмите
Это задание из ОГЭ по математике предлагает найти площади, углы, длины геометрических фигур, нарисованных на фоне в клетку. Задание 18 с кратким ответом, в ответ идет только число.
Реальные задания №18 по геометрии из банка ФИПИ
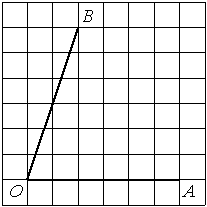
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=6/2=3.
Ответ: 3
AE8B22
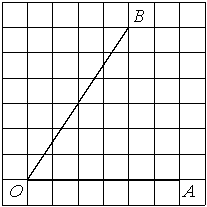
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=6/4=1,5.
Ответ: 1,5
09C3B1
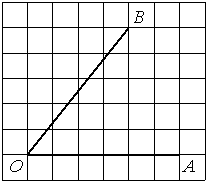
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=5/4=1,25.
Ответ: 1,25
739060
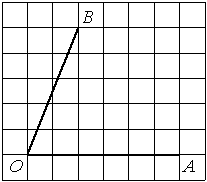
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=5/2=2,5.
Ответ: 2,5
0747AA
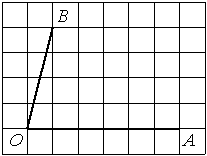
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=4/1=4.
Ответ: 4
9C09A9
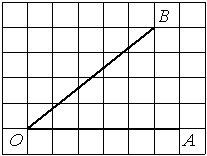
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=4/5=0,8.
Ответ: 0,8
A1ECAA
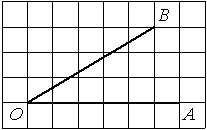
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=3/5=0,6.
Ответ: 0,6
887E42
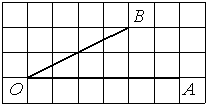
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=2/4=0,5.
Ответ: 0,5
201054
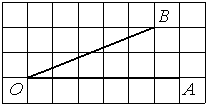
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=2/5=0,4.
Ответ: 0,4
E73651
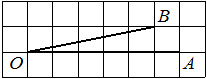
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=1/5=0,2.
Ответ: 0,2
A601D0
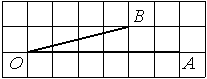
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=1/4=0,25.
Ответ: 0,25
51BEC9
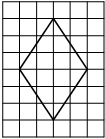
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 6*4=12
Ответ: 12
F519DD
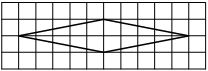
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 10*2=10
Ответ: 10
704DB1
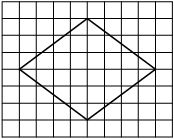
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 6*8=24
Ответ: 24
2F4DA5
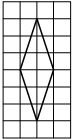
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 6*2=6
Ответ: 6
1F239C
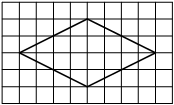
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 8 * 4 = 16
Ответ: 16
33E327
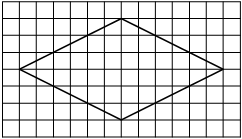
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 6 = 36
Ответ: 36
0B92D0
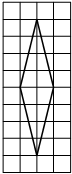
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 8 * 2 = 8
Ответ: 8
3B5D8B
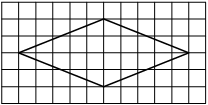
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 4 = 20
Ответ: 20
CFCA33
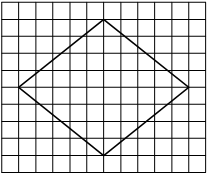
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 8 = 40
Ответ: 40
3B008A
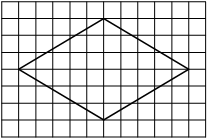
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 6 = 30
Ответ: 30
8372E0
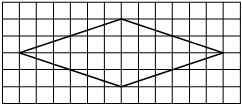
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 4 = 24
Ответ: 24
FFD1EE
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 2 = 12
Ответ: 12
E2A932
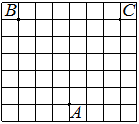
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 3
969F4E
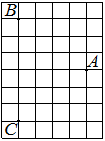
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 5
AFB9A1
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 1
D234F7
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 2
68F679
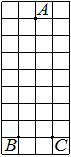
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 4
9672D7
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 5
3F311F
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 6
C598DA
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 8
FCC29D
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 7
0DBF9B
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 6
B73FA9
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 1
78BDFE
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 7
CB1715
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 3
107F53
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 2
5B4C37
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4
FEDC09
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 6
C563EA
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 5
B2853A
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
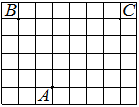
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4
FE13B1
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 2
C8BF73
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
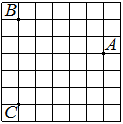
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 5
A4B62F
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 2
DA3762
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 7
C576A6
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
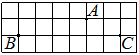
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 1
9D880E
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4
078B48
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
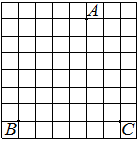
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 6
854014
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 3
B4DCCF
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 8
259D23
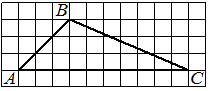
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3
9C2804
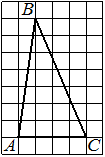
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5
BC4EBE
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2
7ECBCE
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
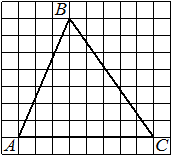
Решение:
Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4
D2D94B
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
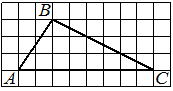
Решение:
Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4
8F5C52
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
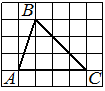
Решение:
Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2
686EFB
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
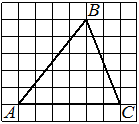
Решение:
Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3
07C968
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
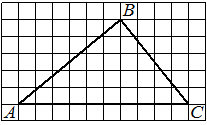
Решение:
Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5
E3456A
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
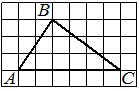
Решение:
Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3
794271
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
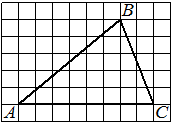
Решение:
Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4
A1906B
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
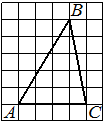
Решение:
Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2
E52B99
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
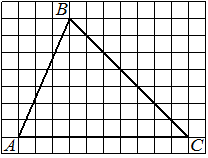
Решение:
Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5
E331C7
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
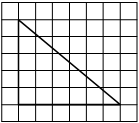
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 6
F7FF65
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
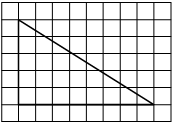
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 8
AAC1BC
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
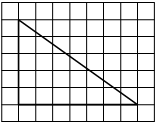
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 7
2BD44A
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
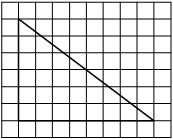
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 8
6DE9A6
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
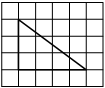
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 4
39A91A
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
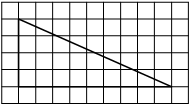
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 9
197283
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
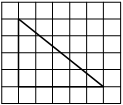
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 5
2EA9C2
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
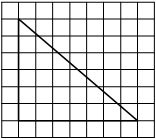
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 7
ED1F0E
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
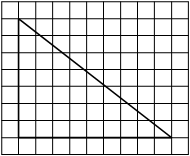
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 9
10323E
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
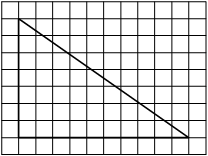
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 10
ED4E1A
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
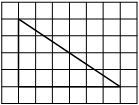
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 6
4FAEEC
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
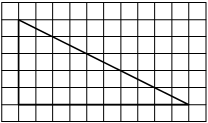
Решение:
Катет – сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 10
F8232E
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
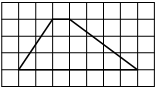
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (1+7) : 2 = 4
Ответ: 4
351A72
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
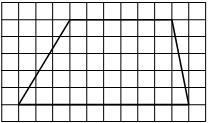
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (6+10) : 2 = 8
Ответ: 8
5EFE19
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
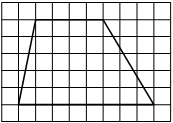
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (4+8) : 2 = 6
Ответ: 6
C05266
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
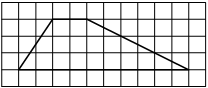
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (2+10) : 2 = 6
Ответ: 6
CFD6D8
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
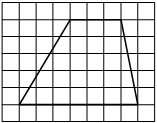
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (3+7) : 2 = 5
Ответ: 5
3BD771
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
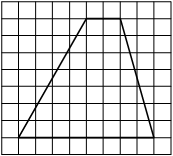
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (2+8) : 2 = 5
Ответ: 5
869450
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
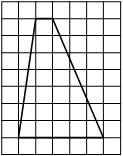
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (1+5) : 2 = 3
Ответ: 3
19D522
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
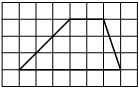
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (2+6) : 2 = 4
Ответ: 4
A28F9D
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
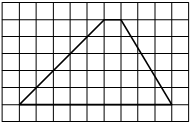
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (1+9) : 2 = 5
Ответ: 5
2EF821
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
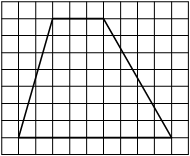
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (3+9) : 2 = 6
Ответ: 6
45A5FF
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
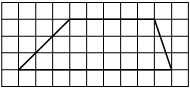
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (5+9) : 2 = 7
Ответ: 7
7AAADC
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
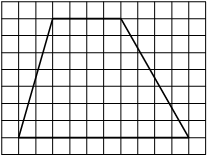
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (4+10) : 2 = 7
Ответ: 7
321F00
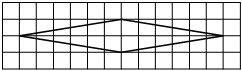
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
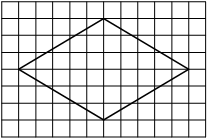
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10
87C214
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
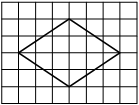
Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 6
6CB64A
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8
4801B0
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12
DEA70E
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8
6D0D8F
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12
8D9098
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8
90A16B
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10
F3D7EA
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10
35106F
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10
1C594B
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 6
E4F439
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:
Диагональ – прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12
657F97
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
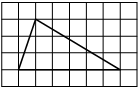
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 6 * 3 = 9
Ответ: 9
E873D3
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
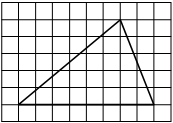
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 5 = 20
Ответ: 20
9E69AF
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
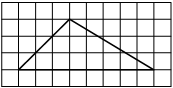
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 3 = 12
Ответ: 12
53C928
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
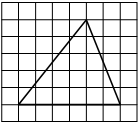
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 6 * 5 = 15
Ответ: 15
EE2C25
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
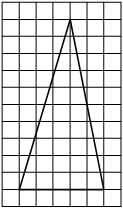
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 5 * 10 = 25
Ответ: 25
1B4EAF
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
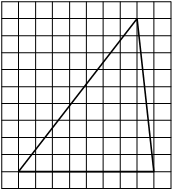
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 9 = 36
Ответ: 36
94B40E
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
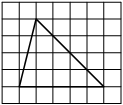
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 5 * 4 = 10
Ответ: 10
F50FF8
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
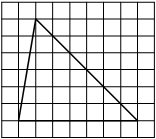
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 6 = 21
Ответ: 21
3A7F81
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
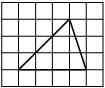
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 4 * 3 = 6
Ответ: 6
DFB4EA
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
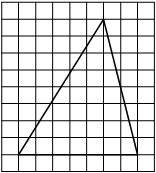
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 8 = 28
Ответ: 28
7AEBD7
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
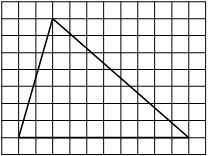
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 10 * 7 = 35
Ответ: 35
4718F7
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
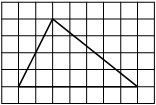
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 2 = 14
Ответ: 14
0C5645
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
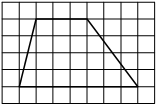
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (7+3) * 4= 20
Ответ: 20
695D77
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
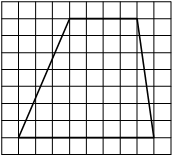
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 7= 42
Ответ: 42
07B1AD
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
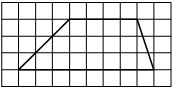
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 3 = 18
Ответ: 18
4774FE
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
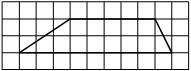
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 2= 14
Ответ: 14
284762
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
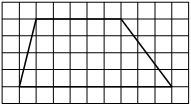
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 4= 28
Ответ: 28
2916B2
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
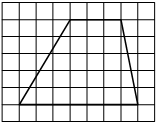
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 5= 25
Ответ: 25
867701
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
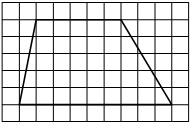
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 5= 35
Ответ: 35
B5D99F
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
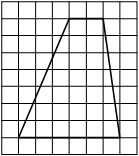
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (2+6) * 7= 28
Ответ: 28
B11571
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
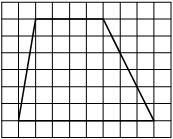
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 6= 36
Ответ: 36
E46263
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
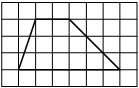
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (2+6) * 3= 12
Ответ: 12
283DE4
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
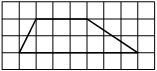
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 2= 10
Ответ: 10
383C46
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
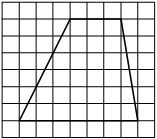
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 6= 30
Ответ: 30
2E7B84
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
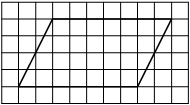
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 4 = 28
Ответ: 28
71E23E
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
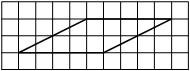
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 2 = 10
Ответ: 10
3BD9B6
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
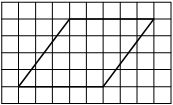
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 4 = 20
Ответ: 20
5C5046
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
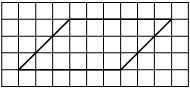
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 3 = 18
Ответ: 18
566A4E
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
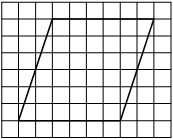
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 6 = 36
Ответ: 36
0275CC
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
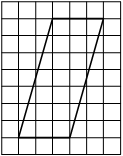
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 3 * 7 = 21
Ответ: 21
E81F8D
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
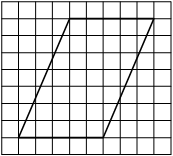
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 7 = 35
Ответ: 35
2A59D7
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 2 = 14
Ответ: 14
5FC71A
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
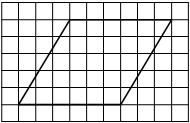
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 5 = 30
Ответ: 30
257B6F
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
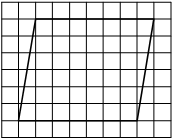
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 6 = 42
Ответ: 42
839354
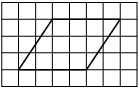
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 4 * 3 = 12
Ответ: 12
C1A1AF
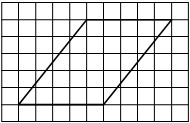
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 5 = 25
Ответ: 25
9B4AE0
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:
Считаем клетки внутри фигуры.
Ответ: 14
11403B
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:
Считаем клетки внутри фигуры.
Ответ: 8
CDF457
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:
Считаем клетки внутри фигуры.
Ответ: 15
06B968
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:
Считаем клетки внутри фигуры.
Ответ: 10
AFB70E
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:
Считаем клетки внутри фигуры.
Ответ: 13
C4025D
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:
Считаем клетки внутри фигуры.
Ответ: 16
E4CBB2
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:
Считаем клетки внутри фигуры.
Ответ: 9
211628
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:
Считаем клетки внутри фигуры.
Ответ: 17
5D3FCF
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:
Считаем клетки внутри фигуры.
Ответ: 19
320729
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:
Считаем клетки внутри фигуры.
Ответ: 18
C72856
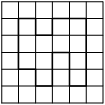
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 12
BB2950
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:
Считаем клетки внутри фигуры.
Ответ: 11
F78C61
