Лучший ответ
Natalinka
Просветленный
(23121)
12 лет назад
Находишь вторую диагональ по теор Пифагора. Площадь ромба равна произведению диагоналей.
Остальные ответы
anastasia.kochura
Профи
(699)
12 лет назад
ромб состоит из 4 прямоугольных треугольников.
диагонали точкой пересечения делятся пополам.
по теореме пифагора найди еще один отрезок диагонали.
площадь треугольника будет равна 1/2катет*катет
ну а потом умнож плошадь треугольника на 4
Оля Борисенко
Ученик
(216)
12 лет назад
У ромба все стороны равны, найти зная все стороны одного треугольника площадь и умножить на 2.
Бунтарка
Профи
(512)
12 лет назад
найди вторую диагональ, площадь равна произведению диагоналей
Орлянский Даниил
Ученик
(111)
5 лет назад
Сторона ромба 4 см, а менша дiагоналi сторонi. Обчислити площу ромба?
Содержание:
- Формулы площади ромба:
- Формула периметра ромба:
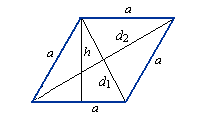
Ромб – это четырёхугольник, у которого все стороны равны.
Ромб можно рассматривать как частный случай параллелограмма, у которого или две смежные стороны равны, или диагонали
взаимно перпендикулярны, или диагональ делит угол пополам. Ромб с прямыми углами называется квадратом.
Формулы площади ромба:
Площадь геометрической фигуры – часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади ромба выражается числом заключающихся в него квадратных единиц.
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
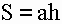
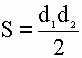
S – площадь ромба
a – длина основания ромба
h – длина высоты ромба
d1 – длина 1-ой диагонали
d2 – длина 2-ой диагонали
См. также: Программа для расчета площади ромба.
Формула периметра ромба:
Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.
1) Периметр ромба равен сумме 4-х длин его сторон или произведению
длины любой его стороны на четыре (так как у ромба длины всех сторон равны).
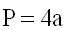
P – периметр ромба
a – длина стороны ромба
Остались вопросы?
Здесь вы найдете ответы.
Что понимается под высотой ромба?
Высота ромба представляет собой перпендикуляр, который опущен из одного из
его углов на сторону, противоположную данному углу.
Высота ромба, опущенная из одного его угла, делит противолежащую сторону
пополам. Как найти величины углов этого ромба?
Обозначим имеющийся ромб как ABCD. Из его угла В проведем высоту ВН, после
чего получим треугольник АВН с прямым углом. Известно, что длина всех
сторон ромба одинаковая, а длина АН равна половине длины АВ. Зная это и
используя теорему, которая является обратной теореме о 30-градусном угле,
можно провести доказательство того, что угол АВН равен 30 градусам.
Учитывая то, что сумма всех углов треугольника равна 180 градусом, можно
найти неизвестную величину третьего угла треугольника:
BAH=180-30-90=60 градусов.
Так, угол АВС равен:
ABC=180-60=120 градусов.
Как найти высоту ромба, если единственной величиной, которая известна,
является длина одной его стороны?
Известна формула площади (S) ромба, которая представляет собой
произведение длины его стороны (а) на высоту (h), проведенную к ней:
S = a*h.
Есть возможность выразить высоту из приведенной выше формулы. Она будет
равна отношению площади ромба к длине его стороны:
h = S/a.
Имеется треугольник с прямым углом и катетами длиной 3 см. и 4 см. Его
площадь аналогична площади ромба со стороной 5 см. Как найти высоту ромба?
Площадь (S) треугольника с прямым углом рассчитывается путем деления
пополам произведения длин его катетов. В данном случае она будет равна:
SΔ = 4*3/2 = 6 см.кв.
Площадь ромба определяется умножением длины его стороны на высоту,
проведенную к ней. Если принять высоту за х, и учесть, что площадь ромба
равна площади прямоугольного треугольника (6 см.кв.), то:
S = 5*x = 6 см.кв.
Отсюда можно найти значение х:
х = 6/5 = 1,2 см.
Ответ: высота ромба составляет 1,2 см.
Как найти высоту ромба при условии, что длины его диагоналей равны 6 см. и 8
см.?
Диагонали, проведенные в ромбе, делят эту фигуру на четыре треугольника,
которые являются равными. Длины катетов этих треугольников составляют 3
см. и 4 см. Такой вывод можно сделать на основании того, что в точке
пересечения диагоналей они делятся пополам. Гипотенуза (с) треугольников
представляет собой сторону ромба. Ее длина равна:
с = √(9+16) = √25 = 5 см.
Следовательно, сторона ромба также равна 5 см.
Площадь ромба высчитывается как произведение длин его диагоналей, деленное
пополам:
S = d1*d2/2 = 6*8/2 = 24 см. кв.
Известна также другая формула, используемая для вычисления площади ромба,
в которой длина его стороны (а) умножается на высоту(h):
S = a*h
Из данной формулы выражаем высоту:
h = S/a = 24/5 = 4,8 см.
Ответ: Высота ромба составляет 4,8 см.
Как найти высоту ромба при условии, что его диагонали равны d1 и d2, а длина
стороны – а?
Высоту ромба можно рассчитать, если его диагонали (d1 и d2)и сторона (а) –
известные величинами. В этом случае для определения неизвестной высоты
следует пользоваться приведенной ниже формулой:
h = (d1 * d2)/a
Площадь ромба составляет 60 см.кв., а его периметр равен 48 см. Как найти
высоту ромба в конкретном случае?
Периметр (Р) ромба равен сумме длин всех его сторон (а) и вычисляется по
следующей формуле:
Р = а+а+а+а
В данном случае периметр ромба равен 48 см., это значит, что:
а+а+а+а = 48 см.
Находим значение а:
а = 48/4 = 12 см.
Площадь ромба (S) является произведением длины его стороны (а) и высоты
(h), проведенной к этой стороне:
S = а*h
В задании сказано, что площадь ромба – 60 см.кв. Значит:
а*h=60
Находим неизвестную высоту:
h=60/а=60/12=5 см.
Ответ: Высота ромба – 5 см.
Как найти высоту ромба, зная о том, что его площадь составляет 48 см.кв., а
периметр – 32 см.?
Согласно формуле расчета периметра (Р) ромба, он равен сумме длин всех его
сторон (а) (Р=а+а+а+а). Известно, что все стороны ромба имеет одинаковую
длину. Из этого следует, что длина одной стороны будет равна ¼ части его
периметра:
а = Р/4 = 32/4 = 8 см.
Площадь (S) ромба можно высчитать путем умножения длины его стороны (а) на
высоту (h), проведенную к ней:
S = а* h
В конкретном случае:
48 = 8* h
Отсюда можем найти высоту (h), разделив площадь на длину стороны ромба:
H = 48/8 = 6 см.
Ответ: Высота ромба составляет 6 см.
Отношение длин диагоналей ромба выглядит как 10/24. Его периметр равен 52
см. Как найти высоту ромба в данном случае?
Периметр (Р) ромба равен сумме длин всех его сторон (а), длины которых
равны. Это значит:
Р = 4*а
По условию задачи:
52 = 4*а
Следовательно:
а = 52/13 = 13 см.
Предположим, что длина одной из диагоналей ромба равна 10х, тогда длина
второй его диагонали будет выглядеть как 24х. Отношение их длин можно
записать в следующем виде:
10х:24х=10:24
Доказано, что диагонали ромба взаимно перпендикулярны и в точке
пересечения они делятся пополам, при этом образуя четыре равных
треугольника с прямым углом.
Теорема Пифагора гласит, что сумма длин его катетов, возведенных во вторую
степень, равна длине гипотенузы, которая также возведена в квадрат:
с2 = а2 + b2
Для данной задачи это равенство записывается так:
(5х)²+(12х)²=13²
Отсюда видно, что:
169х²=169; следовательно, х2 = 1. Значит х тоже будет равен 1.
Длина диаметра, обозначенного как 10х, равна 10 см. (10*1), а длина
второго диаметра, который обозначен как 24х, равна 24 см. (24*1).
Площадь (S) ромба рассчитывается как:
S = d₁*d₂/2 или a·h
Из этого можно составить следующее уравнение:
d₁*d₂=2a*h
Выражаем h и получаем:
h= d₁*d₂/2*а=10·24:26=240/26=120/13 см.
Какая формула используется с целью вычисления высоты ромба?
Ромб имеет четыре высоты. Все они имеют равные длины. Вывод об этом можно
сделать, рассмотрев все треугольные фигуры, элементами которых являются
эти высоты. Есть возожность высчитать высоту ромба при помощи различных
параметров, которые могут быть указаны в условии конкретной задачи.
Предположим, что нам известна площадь (S) ромба и длина его стороны (а). В
этом случае высота ромба будет равна отношению его площади к длине высоты:
h = S/a.
Если же по условию задачи известны длины диагоналей ромба d1 и d2, а также
его сторона а, то высоту можно рассчитать так: h = (d1*d2 )/a.
В случае, когда известна длина стороны (а) ромба и угол А, находящийся
между смежными сторонами, то для расчета высоты ромба используется
следующая формула:
h = a*a*sin A /a = a*sin A.
Существуют также и другие варианты вычисления длины высоты ромба на
основании того, какие величины будут известны по условию задания. Однако
ключевыми параметрами, используя которые можно вычислить высоту ромба,
являются диагонали, длина любой его стороны и угол, образованный между
смежными сторонами.
В каком виде записываются формулы, используемые для определения площади
ромба?
Площадь ромба можно рассчитать одним из трех способов:
1. S = a² sin a, в которой α — образованный двумя сторонами угол, a —
сторона.
2. S = ah, или Длина стороны ромба, умноженная на его высоту.
3. S = (d1*d2)/2, в которой d1 и d2 – длины диагоналей фигуры.
На сторону ромба опущена высота, которая на 1,7 см. меньше ее длины.
Периметр фигуры составляет 32 см. Как в данном случае вычислить площадь
ромба?
Зная, чему равен периметр ромба, можно вычислить длину его стороны:
Р/4 = 8 см.
Известно, что высота данной фигуры меньше ее стороны на 1,7 см. Теперь
можем определить длину высоты:
h = 8-1,7 = 6,3 см.
Площадь ромба можно найти, умножив его сторону на высоту, которая на нее
опущена:
8 * 6,3 = 50,4 см².кв.
Ответ: S = 50,4 см. кв.
Известно, что диагонали ромба относятся как 4/3, а его сторона составляет 10
см. Как найти площадь ромба?
Если длины диагоналей фигуры относятся как 4/3, то их половины будут
относиться также:
(4d)²+(3d)²=10² = 16d²+9d² = 100
Отсюда:
25d²=100
d =2,
Значит:
d¹/2 = 4d = 8 см.
d²/2 = 3d = 6 см.
Теперь можно найти площадь:
S= 2*d¹/2*d²/2=2*8*6 = 96 см.кв.
Ответ: S ромба = 96 см.кв.
Как записывается формула расчета площади ромба через длины его диагоналей d1
и d2?
Площадь ромба можно описать как сумму площадей 2-х треугольных фигур,
основанием которых является одна диагональ, а вторая диагональ ромба
представляет собой сумму длин высот этих фигур. Диагонали ромба при
пересечении образуют угол в 90 градусов. На основании этого можно найти
площадь ромба следующим образом:
S = ½ d1*d2.
Как записать формулу вычисления площади ромба через диагонали?
Известно, что, пересекаясь, диагонали ромба образуют угол в 90 градусов и
в точке пересечения делятся пополам.
Для расчета площади ромба через диагонали нужно перемножить их длины, а
затем разделить полученное число на два:
S = ½ d1*d2.
Для примера можно рассмотреть ромб, одна диагональ которого равна 5 см., а
вторая – 4 см. Тогда его площадь будет равна:
S=1/2*5*4=10 см. кв.
Как выглядит формула для определения площади ромба?
S ромба возможно вычислить, перемножив длину одной из его сторон (а) и
высоту (h). Формула записывается так:
S=a*h.
См. также: Программа для расчета периметра ромба.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Ромб – это геометрическая фигура; параллелограмм, имеющие 4 равные стороны.
-
Формула вычисления площади
- По длине стороны и высоте
- По длине стороны и углу
- По длинам диагоналей
- Примеры задач
Формула вычисления площади
По длине стороны и высоте
Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a ⋅ h

По длине стороны и углу
Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:
S = a 2 ⋅ sin α

По длинам диагоналей
Площадь ромба равна одной второй произведения его диагоналей.
S = 1/2 ⋅ d1 ⋅ d2

Примеры задач
Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.
Решение:
Используем первую формулу, рассмотренную выше: S = 10 см ⋅ 8 см = 80 см2.
Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.
Решение:
Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см)2 ⋅ sin 30° = 36 см2 ⋅ 1/2 = 18 см2.
Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.
Решение:
Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 ⋅ 4 см ⋅ 8 см = 16 см2.
Download Article
Download Article
A rhombus is a parallelogram with four congruent sides. It does not have to have right angles.[1]
There are three formulas for finding the area of a rhombus. Just follow these steps if you want to know how to do it.
-

1
Find the length of each diagonal. The diagonals of a rhombus are the lines that connect the opposite vertices (corners) in the center of the shape. The diagonals of a rhombus are perpendicular and form four right triangles through their intersection.[2]
- Let’s say the diagonals are 6 cm. and 8 cm. long.
-

2
Multiply the length of the diagonals. Just write down the length of the diagonals and multiply them. In this case, 6 cm x 8 cm = 48 cm2. Don’t forget to square the units since you’re working in square units.[3]
Advertisement
-

3
Divide the result by 2. Since 6 cm x 8 cm = 48 cm2, just divide the result by 2. 48 cm2/2 = 24 cm2. The area of the rhombus is 24 cm2.[4]
Advertisement
-

1
Find the base and the height.[5]
You can also think of this as multiplying the altitude of the rhombus with the length of the side of the rhombus. Let’s say the height of the rhombus is 7 cm and the base is 10 cm. -

2
Multiply the base and height. Once you know the base and height of the rhombus, all you have to do to find the area of the shape is to multiply them. So, 10 cm x 7 cm = 70 cm2. The area of the rhombus is 70 cm2.[6]
Advertisement
-

1
Square the length of any side. A rhombus has four equal sides, so it doesn’t matter which side you choose. Let’s say the side is 2 cm long. 2 cm x 2 cm = 4 cm2.[7]
-

2
Multiply it by the sine of one of the angles. It doesn’t matter which angle you choose. Let’s say one of the angles is 33 degrees. Just multiply sine (33) by 4 cm2 to get the area of the rhombus. (2 cm)2 x sine (33) = 4 cm2 x 0.55 = 2.2 cm2. The area of the rhombus is 2.2 cm2.[8]
Advertisement
Rhombus Area Calculator, Practice Problems, and Answers
Add New Question
-
Question
How do I find the perimeter of a rhombus?

Perimeter = sum of all sides. The rhombus has equal sides, so its perimeter = side x 4.
-
Question
How can I find the height of a rhombus?

In a rhombus, the diagonals bisect and are perpendicular, meaning that inside the rhombus there are four right-angle triangles, with side lengths half that of the diagonals, use the pythagoran theorem to find the hypotenuses a² + b² = c²
Now we have the base, given any of the angles inside the rhombus, we can find all of them because they are corresponding and all add up to 360 degrees, once we have all of the angles, another two identical triangles appear. we only have to use one of these as they are identical.
Now we have the hypotenuse and an angle of this triangle so using trigonometry we can find the adjacent side which is the height of the rhombus.
-
Question
How do I determine the perimeter given one diagonal and the area?

Use the Pythagorean theorem to find the sides and then find the perimeter.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
A rhombus is a shape with four equal sides, each of which is parallel to the opposite side. While a square is a type of rhombus, they can also be diamond-shaped, with angles of greater or less than 90° at each corner. There are several easy ways to find the area of a diamond-shaped rhombus. One is to measure the rhombus diagonally from corner to corner, each way. For instance, let’s say your rhombus measures 10 cm across lengthwise and 6 cm across widthwise. Once you find the length of each diagonal, multiply the lengths together. In this case, 10 cm x 6 cm = 60 cm. Finally, divide the result by 2. Don’t forget to square your units when you write the result, since you’re measuring the area. 60/2 = 30, so our rhombus has an area of 30 cm squared. Another simple method is to multiply the base length of the rhombus by its height. Measure the width of the bottom line of the rhombus, then take a perpendicular measurement from the base to the opposite line at the top. Multiply the measurements together to find the area. For instance, if a rhombus is 12 cm long at the base and has a height of 8 cm, the area of the rhombus would be 96 cm squared. If you only know the length of one side of the rhombus and one of the angles, you can still figure out the area using trigonometry. To do this, square the length of the known side, then multiply the result by the sine of one of the angles. For instance, if the rhombus has one side with a length of 6 cm, and you know it contains a 45° angle, the area would be 36 cm squared x sin(45°), or approximately 30.63 cm squared. If you want to learn how to use trigonometry to find the area of the rhombus, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 892,776 times.
Did this article help you?
Площадь ромба
1. Площадь ромба равна произведению стороны на высоту, проведенную к этой стороне (рис. 1), то есть
(
S=a h
)
2. Если известна сторона ромба (у ромба все стороны равны) и угол между сторонами (рис. 1), то площадь можно найти по следующей формуле:
(
S=a^{2} sin alpha
)
3. Площадь ромба также равна полупроизведению диагоналей, то есть:
(
S=frac{d_{1} d_{2}}{2}
)
4. Если известен радиус r окружности, вписанной в ромб (рис. 1), и сторона ромба a, то его площадь вычисляется по формуле:
(
S=2 a r
)
Примеры решения задач
ПРИМЕР 1
Найти площадь ромба с диагоналями 10 см и 6 см.
Искомая площадь равна половине произведения диагоналей, то есть
(
S=frac{1}{2} cdot 10 cdot 6=30
) (см2)
Площадь ромба равна (
mathrm{S}=30 mathrm{см} 2
)
ПРИМЕР 2
Найти площадь ромба, если его сторона равна 5, а большая диагональ – 8.
Сделаем рисунок (рис. 2).
Обозначим меньшую диагональ ромба (
mathrm{d} 2
), то есть (
A C=d 2
). Согласно свойства ромба, его диагонали пересекаются под прямым углом и точкой пересечения делятся пополам.
Рассмотрим прямоугольный треугольник (
mathrm{AOD}
). Тогда по теореме Пифагора:
(
5^{2}=left(frac{d_{2}}{2}right)^{2}+left(frac{8}{2}right)^{2} Rightarrow frac{d_{2}^{2}}{4}=25-16
)
(
d_{2}^{2}=4 cdot 9 Rightarrow d_{2}=sqrt{36}=6
)
А тогда искомая площадь
(
S=frac{8 cdot 6}{2}=24
)
(
mathrm{S}=24
)
