Как рассчитать площадь ромба
На данной странице калькулятор поможет рассчитать площадь ромба онлайн. Для расчета задайте длину основания, высоту или длины диагоналей и угол между ними.
Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом.
Через сторону и высоту
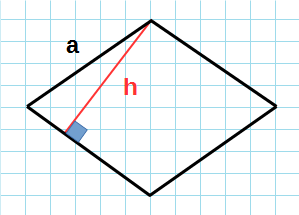
Формула для нахождения площади ромба через сторону и высоту:
a – сторона ромба; h – высота ромба.
Через диагонали
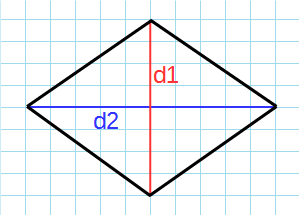
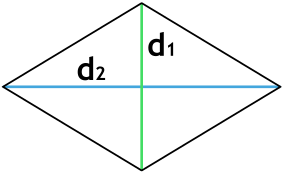
Формула для нахождения площади ромба через диагонали:
d1, d2 – диагонали ромба.
Через сторону и угол
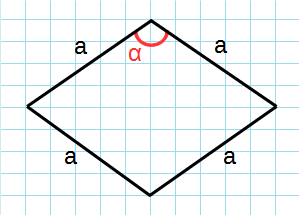
Формула для нахождения площади ромба через сторону и угол:
a – сторона ромба; α – угол между сторонами.
Через угол и диагональ из этого угла
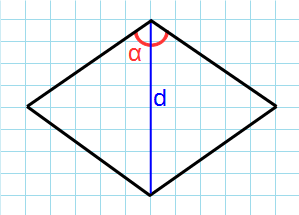
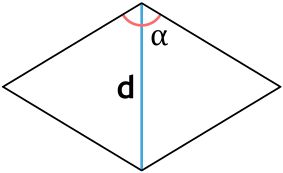
Формула для нахождения площади ромба через угол и диагональ выходящая из этого угла:
d – диагональ ромба; α – угол между сторонами.
Через угол и противолежащию диагональ
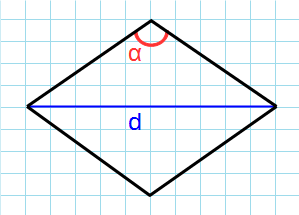
Формула для нахождения площади ромба через угол и диагональ противолежащая углу:
d – диагональ ромба; α – угол между сторонами.
Через угол и радиус вписанной окружности
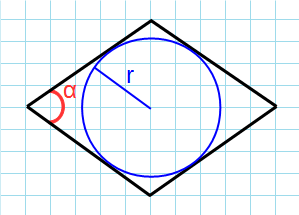
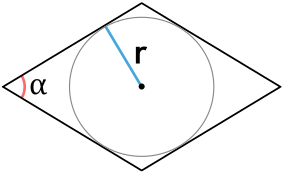
Формула для нахождения площади ромба через угол и радиус вписанной окружности:
r – радиус окружности; α – угол между сторонами.
Через сторону и радиус вписанной окружности
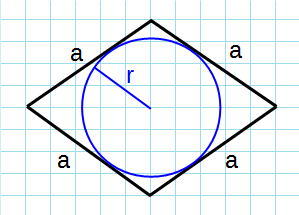
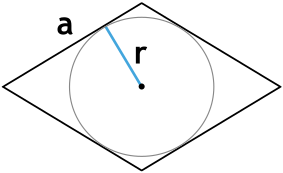
Формула для нахождения площади ромба через сторону и радиус вписанной окружности:
a – сторона ромба; r – радиус вписанной окружности.

{S = a^2 cdot sin (alpha)}
На этой странице мы предлагаем вам 7 формул площади ромба. Для каждой формулы можно воспользоваться онлайн калькулятором и мгновенно получить результат, не прибегая к помощи обычного калькулятора
Содержание:
- калькулятор площади ромба
- формула площади ромба через сторону и угол
- формула площади ромба через сторону и высоту
- формула площади ромба через диагонали
- формула площади ромба через угол и диагональ из угла
- формула площади ромба через угол и противолежащую диагональ
- формула площади ромба ромба через радиус вписанной окружности и угол
- формула площади ромба через радиус вписанной окружности и сторону
- примеры задач
Формула площади ромба через сторону и угол
S = a^2 cdot sin (alpha)
a – сторона ромба
α – угол между сторонами ромба
Формула площади ромба через сторону и высоту
S = a cdot h
a – сторона ромба
h – высота ромба
Формула площади ромба через диагонали
S = dfrac{d_1 cdot d_2}{2}
d1 и d2 – диагонали ромба
Формула площади ромба через угол и диагональ из угла
S = dfrac{d^2}{2} cdot \tg(dfrac{alpha}{2})
d – диагональ ромба
α – угол между сторонами ромба, из которого выходит диагональ
Формула площади ромба через угол и противолежащую диагональ
S = dfrac{d^2}{2} cdot ctg(dfrac{alpha}{2})
d – диагональ ромба, противоположная углу α
α – угол между сторонами ромба
Формула площади ромба через радиус вписанной окружности и угол
S = dfrac{4r^2}{sin(alpha)}
r – радиус окружности
α – угол между сторонами ромба
Формула площади ромба через радиус вписанной окружности и сторону
S = 2ar
r – радиус окружности
a – сторона ромба
Примеры задач на нахождение площади ромба
Задача 1
Найдите площадь ромба если его диагонали равны 34 и 4.
Решение
Для решения задачи воспользуемся формулой площади ромба через диагонали.
S = dfrac{d_1 cdot d_2}{2} = dfrac{34 cdot 4}{2} = 68 : см^2
Ответ: 68 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь ромба если его диагонали равны 4 и 6.
Решение
Задача аналогична предыдущей.
S = dfrac{d_1 cdot d_2}{2} = dfrac{4 cdot 6}{2} = 12 : см^2
Ответ: 12 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь ромба стороны которого равны 5, а высота равна 4.
Решение
Воспользуемся формулой площади ромба через высоту и сторону.
S = a cdot h = 5 cdot 4 = 20 : см^2
Ответ: 20 см²
Проверим полученный ответ на калькуляторе .
Ромб – это геометрическая фигура; параллелограмм, имеющие 4 равные стороны.
-
Формула вычисления площади
- По длине стороны и высоте
- По длине стороны и углу
- По длинам диагоналей
-
Примеры задач
Формула вычисления площади
По длине стороны и высоте
Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a ⋅ h
По длине стороны и углу
Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:
S = a 2 ⋅ sin α
По длинам диагоналей
Площадь ромба равна одной второй произведения его диагоналей.
S = 1/2 ⋅ d1 ⋅ d2
Примеры задач
Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.
Решение:
Используем первую формулу, рассмотренную выше: S = 10 см ⋅ 8 см = 80 см2.
Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.
Решение:
Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см)2 ⋅ sin 30° = 36 см2 ⋅ 1/2 = 18 см2.
Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.
Решение:
Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 ⋅ 4 см ⋅ 8 см = 16 см2.
Ромб — это параллелограмм, в котором все стороны равны друг другу.
Онлайн-калькулятор площади ромба
Если стороны ромба образуют прямой угол, то получим квадрат.
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.
Площадь ромба, как и площади большинства геометрических фигур, можно найти несколькими способами. Разберемся в их сути и рассмотрим примеры решений.
Формула площади ромба по стороне и высоте
Пусть нам дан ромб со стороной aa и высотой hh, проведенной к этой стороне. Так как ромб это параллелограмм, то его площадь мы находим так же, как и площадь параллелограмма.
S=a⋅hS=acdot h
aa — сторона;
hh — высота, опущенная на сторону aa.
Решим простой пример.
Сторона ромба равна 5 (см.). Высота, опущенная к этой стороне, имеет длину 2 (см.). Найти площадь ромба SS.
Решение
a=5a=5
h=2h=2
Пользуемся нашей формулой и вычисляем:
S=a⋅h=5⋅2=10S=acdot h=5cdot 2=10 (см. кв.)
Ответ: 10 см. кв.
Формула площади ромба через диагонали
Здесь все так же просто. Нужно просто взять половину произведения диагоналей и получить площадь.
S=12⋅d1⋅d2S=frac{1}{2}cdot d_1cdot d_2
d1,d2d_1, d_2 — диагонали ромба.
Одна из диагоналей ромба равна 7 (см.), а другая в 2 раза больше первой. Найдите площадь фигуры.
Решение
d1=7d_1=7
d2=2⋅d1d_2=2cdot d_1
Найдем вторую диагональ:
d2=2⋅d1=2⋅7=14d_2=2cdot d_1=2cdot 7=14
Тогда площадь:
S=12⋅7⋅14=49S=frac{1}{2}cdot7cdot14=49 (см. кв.)
Ответ: 49 см. кв.
Формула площади ромба через две стороны и угол между ними
S=a2⋅sin(α)S=a^2cdotsin(alpha)
aa — сторона ромба;
αalpha — любой угол ромба.
Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.
Решение
a=10a=10
α=30∘alpha=30^{circ}
По формуле получаем:
S=a2⋅sin(α)=100⋅sin(30∘)=50S=a^2cdotsin(alpha)=100cdotsin(30^{circ})=50 (см. кв.)
Ответ: 50 см. кв.
Формула площади ромба по радиусу вписанной окружности и углу
S=4⋅r2sin(α)S=frac{4cdot r^2}{sin(alpha)}
rr — радиус вписанной окружности в ромб;
αalpha — любой угол ромба.
Найти площадь ромба, если угол между основаниями равен 60 градусов, а радиус вписанной окружности – 4 (см.).
Решение
r=4r=4
α=60∘alpha=60^{circ}
S=4⋅r2sin(α)=4⋅16sin(60∘)≈73.9S=frac{4cdot r^2}{sin(alpha)}=frac{4cdot 16}{sin(60^{circ})}approx73.9 (см. кв.)
Ответ: 73.9 см. кв.
Формула площади ромба по радиусу вписанной окружности и стороне
S=2⋅a⋅rS=2cdot acdot r
aa —сторона ромба;
rr — радиус вписанной окружности в ромб.
Возьмем условие из предыдущей задачи, но пусть вместо угла нам известна сторона ромба, равная 5 см.
Решение
a=5a=5
r=4r=4
S=2⋅a⋅r=2⋅5⋅4=40S=2cdot acdot r=2cdot5cdot4=40 (см. кв.)
Ответ: 40 см. кв.
Ищете того, кто сможеит помочь вам решить контрольную работу по геометрии? Наши эксперты окажут вам быструю и качественную помощь с выполнением работы!
Тест на тему “Площадь ромба”
Rhombus is a special type of Parallelogram which is of huge importance. In a rhombus, all four sides are equal and opposite pairs of lines are congruent, also opposite angles in a rhombus are equal. Rhombus often gets confused with square but Rhombus is very different from the square. Why a rhombus is not considered a square is explained here. Area of the Rhombus is the space occupied by the boundaries of the Rhombus in 2-D space. Area of the Rhombus can be calculated using various methods some of which are discussed in this article.
What is Area of a Rhombus?
Area of the rhombus is considered as the space enclosed by the Rhombus in the 2-D plane. It depends on the dimensions of the rhombus. It is measured in square units, such as square meters, square centimeters, etc. Area of Rhombus is measured using the formulas listed below
Area of Rhombus Formula
Area of the rhombus can be found using various methods some of them are listed in the table below
| Formulas for finding the Area of Rhombus | |
|---|---|
| If Base and Height are given | A = b × h |
| If Diagonals are given | A = ½ × D × d |
| If Base and Interior angle is given | A = b2 × Sin(a) |
Where,
D = length of first diagonal
d = length of second diagonal
b = length of side of rhombus
h = height of rhombus
a = measure of an interior angle
Derivation of Area Formula for Rhombus
Let us consider a rhombus ABCD with O as the point of intersection of two diagonals AC and BD.
The area of rhombus will be
Area = 4 × area of △AOB
= 4 × (1/2) × AO × OB sq.units
= 4 × (1/2) × (1/2) d1 × (1/2) d2 sq.unit
= 4 × (1/8) d1 × d2
= 1/2 d1 × d2
Therefore, the area of a rhombus is A = 1/2 d1 × d2.
How to Find the Area of a Rhombus?
The area of a rhombus is the total space covered or enclosed by the rhombus on a two-dimensional plane. The area of the rhombus can be calculated by three different methods by using diagonal, using base and height, and using trigonometry.
Different methods for finding area of Rhombus are given below
Area of Rhombus using Diagonal
Area = (d1 × d2)/2 sq. units
Where,
d1 is the length of diagonal 1
d2 is the length of diagonal 2
Example 1: Find the area of a rhombus having diagonals 16 m and 18 m.
Solution:
Diagonal 1, d1 = 16 m
Diagonal 2, d2 = 18 m
Area of a rhombus, A = (d1 × d2) / 2
= (16 × 18) / 2
= 288 / 2
= 144 m2
Thus, the area of the rhombus is 144 m2
Area of Rhombus using Base and Height
Area of a Rhombus = b × h sq units
Where,
b is the length of any side of the rhombus
h is the height of the rhombus
Example 2: Find the area of a rhombus having base of 12 m and height is 16 m.
Solution:
Base, b = 12 m
Height, h = 16 m
Area, A = b × h
= 12 × 16 m2
A = 192 m2
Thus, the area of the rhombus is 192 m2
Area of Rhombus using Trigonometric Ratios
Area of a Rhombus = b2 × sin(A) sq. units
Where,
b is the length of any side of the rhombus
A is a measure of any interior angle
Example 3: Find the area of a rhombus if the length of its side is 12 m and one of its angles A is 60°
Solution:
Side = s = 12 m
Angle A = 60°
Area = s2 × sin (60°)
A = 144 × √3/2
A = 72√3 m2
Solved Examples on Area of Rhombus
Example 1: Calculate the area of a rhombus (using base and height) if its base is 5cm and height is 3cm.
Solution:
Given,
Base (b) = 5cm
height of rhombus(h) = 3cm
Now,’
Area of the rhombus(A) = b × h
= 5 × 3
= 15cm2
Example 2: Calculate the area of a rhombus (using diagonal) having diagonals equal to 4cm and 3cm.
Solution:
Given,
Length of diagonal 1 (d1) = 4cm
Length of diagonal 2 (d2) = 3cm
Now,
Area of Rhombus (A) = 1/2 d1 × d2
= 4 x3/2 = 6cm2
Example 3: Calculate the area of the rhombus (using trigonometry) if its side is 8cm and one of its angles A is 30 degrees.
Solution:
Side of the rhombus (b) = 8cm
angle (a) = 30 degrees
Now,
Area of the rhombus(A) = b2 × sin(a)
= (8) × sin(30)
= 64 × 1/2 = 32 cm2
Example 4: Calculate the base of a rhombus if its area is 25cm2 and height is 10cm.
Solution:
Given,
Area = 25 cm2
height of rhombus(h) = 10 cm
Now,
Area of the rhombus(A) = b × h
25 = b × 10
= 2.5 cm
FAQs on Area of Rhombus
Question 1: What do we mean by Rhombus?
Answer:
A rhombus is a type of quadrilateral whose opposite sides are parallel and equal. Also, the opposite angles of a rhombus are equal and the diagonals bisect each other at right angles.
Question 2: Give the Formula for finding the Area of a Rhombus.
Answer:
For finding the area of a rhombus, the given formula is used:
A = ½ × d1 × d2
where, d1 and d2 are diagonals of rhombus
Question 3: How to calculate the perimeter of a rhombus?
Solution:
The perimeter of a rhombus can be calculated by the formula
P= 4b units
where b is a side of the rhombus.
Question 4: How to Find the Area of a Rhombus When the Side and Height are Given?
Answer:
The area of a rhombus its height and side are given is calculated using
A = Base × Height sq units
Question 5: Can area of a rhombus be same as the area of a square?
Answer:
No, The area of a rhombus is not the same as the area of a square. The area of a square is the square of its side, whereas the area of a rhombus is the half the product of diagonal 1 and diagonal 2.
Question 6: Write the Difference between Area of Rhombus and Perimeter of Rhombus.
Answer:
Perimeter of a rhombus is the measure of its boundary and it is calculated by adding the length of all its sides i.e. Perimeter = 4 × sides, whereas area of Rhombus is the product of its base and height, i.e., Area = base × height.
Last Updated :
25 Aug, 2022
Like Article
Save Article