Ромб — это параллелограмм, в котором все стороны равны друг другу.
Онлайн-калькулятор площади ромба
Если стороны ромба образуют прямой угол, то получим квадрат.
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.
Площадь ромба, как и площади большинства геометрических фигур, можно найти несколькими способами. Разберемся в их сути и рассмотрим примеры решений.
Формула площади ромба по стороне и высоте
Пусть нам дан ромб со стороной aa и высотой hh, проведенной к этой стороне. Так как ромб это параллелограмм, то его площадь мы находим так же, как и площадь параллелограмма.
S=a⋅hS=acdot h
aa — сторона;
hh — высота, опущенная на сторону aa.
Решим простой пример.
Сторона ромба равна 5 (см.). Высота, опущенная к этой стороне, имеет длину 2 (см.). Найти площадь ромба SS.
Решение
a=5a=5
h=2h=2
Пользуемся нашей формулой и вычисляем:
S=a⋅h=5⋅2=10S=acdot h=5cdot 2=10 (см. кв.)
Ответ: 10 см. кв.
Формула площади ромба через диагонали
Здесь все так же просто. Нужно просто взять половину произведения диагоналей и получить площадь.
S=12⋅d1⋅d2S=frac{1}{2}cdot d_1cdot d_2
d1,d2d_1, d_2 — диагонали ромба.
Одна из диагоналей ромба равна 7 (см.), а другая в 2 раза больше первой. Найдите площадь фигуры.
Решение
d1=7d_1=7
d2=2⋅d1d_2=2cdot d_1
Найдем вторую диагональ:
d2=2⋅d1=2⋅7=14d_2=2cdot d_1=2cdot 7=14
Тогда площадь:
S=12⋅7⋅14=49S=frac{1}{2}cdot7cdot14=49 (см. кв.)
Ответ: 49 см. кв.
Формула площади ромба через две стороны и угол между ними
S=a2⋅sin(α)S=a^2cdotsin(alpha)
aa — сторона ромба;
αalpha — любой угол ромба.
Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.
Решение
a=10a=10
α=30∘alpha=30^{circ}
По формуле получаем:
S=a2⋅sin(α)=100⋅sin(30∘)=50S=a^2cdotsin(alpha)=100cdotsin(30^{circ})=50 (см. кв.)
Ответ: 50 см. кв.
Формула площади ромба по радиусу вписанной окружности и углу
S=4⋅r2sin(α)S=frac{4cdot r^2}{sin(alpha)}
rr — радиус вписанной окружности в ромб;
αalpha — любой угол ромба.
Найти площадь ромба, если угол между основаниями равен 60 градусов, а радиус вписанной окружности – 4 (см.).
Решение
r=4r=4
α=60∘alpha=60^{circ}
S=4⋅r2sin(α)=4⋅16sin(60∘)≈73.9S=frac{4cdot r^2}{sin(alpha)}=frac{4cdot 16}{sin(60^{circ})}approx73.9 (см. кв.)
Ответ: 73.9 см. кв.
Формула площади ромба по радиусу вписанной окружности и стороне
S=2⋅a⋅rS=2cdot acdot r
aa —сторона ромба;
rr — радиус вписанной окружности в ромб.
Возьмем условие из предыдущей задачи, но пусть вместо угла нам известна сторона ромба, равная 5 см.
Решение
a=5a=5
r=4r=4
S=2⋅a⋅r=2⋅5⋅4=40S=2cdot acdot r=2cdot5cdot4=40 (см. кв.)
Ответ: 40 см. кв.
Ищете того, кто сможеит помочь вам решить контрольную работу по геометрии? Наши эксперты окажут вам быструю и качественную помощь с выполнением работы!
Тест на тему “Площадь ромба”
|
Как найти площадь ромба если известны диагонали ?
Это еще школьный материал, все подобные задачи решали на уроках геометрии. Что же такое ромб. Это 4-х угольная фигура с 4-мя сторонами, у которой противоположные стороны параллельны друг другу и по длине одинаковые. Ромб очень похож на квадрат. Если нам известны диагонали, то формула вычисления площади фигуры следующая: S=d1*d2/2, в формуле d1,d2 – это диагонали фигуры. модератор выбрал этот ответ лучшим Alexsandr82 5 лет назад Чтобы найти площадь ромба если известны обе его диагонали нужно просто их перемножить изатем разделить на два. Сложнее бывает если известна только одна диагональ, а вторую нужно найти, зная один из углов ромба или известен радиус вписанной окружности и один из углов ромба. В таких случаях сначала ищем неизвестную диагональ, а затем находим площать ромба. Формула рассчета диагоналей если известны угол и вторая диагональ: d1 = d2*tg(b/2) d2 = d1*tg(a/2) Где d1 – большая диагональ, d2 – малая, а – меньший угол ромба, b – больший угол. Формула для рассчета диагоналей ромба если известен один угол и радиус вписанной окружности: d1 = 2r/sin(a/2) d2 = 2r/sin(b/2) Зная обе диагонали мы можем рассчитать площадь ромба.
Думаю, что эту формулу можно легко вывести самой. Достаточно представить себе ромб и провести некоторые дополнительные построения, чтобы сделать из ромба более простую фигуру. А именно легко заметить, что диагонали ромба разбивают его на четыре одинаковых прямоугольных треугольника. Если каждый такой треугольник, удвоить, отразить относительно гипотенузы, то есть стороны ромба, то вместо ромба мы получим прямоугольник. То есть мы на диагоналях ромба строим прямоугольник, у которого параллельные стороны равны соответствующей диагонали. А площадь прямоугольника равна а*b или в нашем случае d*d. Но этот прямоугольник в два раза больше нашего ромба, а следовательно формула площади ромба примет вид S=d*d/2.
Ксарфакс 6 лет назад Если известны диагонали ромба a и b, то можно легко найти его площадь. Она будет равна: S(ромба) = 0,5*a*b, то есть половина произведения диагоналей. Доказательство Диагонали ромба разбивают его на 4 равных прямоугольных треугольника. Катеты каждого из них равны половине диагоналей: 0,5a и 0,5b.
Площадь прямоугольного треугольника равна половине произведения катетов. Соответственно, площадь ромба равна 4 площадям одного треугольника, который был образован пересечением диагоналей. S(ромба) = 4*(0,5a*0,5b*0,5) = 4*0,125*a*b = 0,5a*b. Что и требовалось доказать. Пример Диагональ a = 4 см. Диагональ b = 8 см. S(ромба) = 0,5*4*8 см. = 16 см.
Алиса в Стране 5 лет назад Очень даже просто. Существует очень простая специальная математическая формула для этого случая, которую дети изучают в школах: d1 х d2 / 2, где d1 и d2 – это диагонали ромба. Звучит это так: чтобы найти площадь ромба нужно перемножить его диагонали и поделить это произведение на два. Таня Ляпаева 8 лет назад Хм…У ромба стороны противоположны, он же и параллелограмм. Если нам известны диагонали, то можно вычесть площадь из этой фигуры. Пусть диагонали b1 и b2, тогда Площадь (S) = b1*b2/b2. Мы просто перемножаем эти диагонали и делаем все по формуле. Юлия1578 9 лет назад Задача очень простая. Нужно только логически поразмыслить и вспомнить одну простую математическую формулу. Чтобы вычислить искомую площадь ромба, зная параметры диагонали, выполняем всего два арифметических действия:
Артём Денисов 7 лет назад Если известны только параметры диагоналей, то чтобы отыскать площадь самой фигуры, следует перемножить сами диагонали ((S) = d1*d2/d2). Где S – площадь, а d1 и d2 – диагонали. Именно таким образом и находится площадь ромба, когда известны лишь диагонали этой фигуры. Внутри ромба имеется четыре прямоугольных треугольника. площадь одного треугольника равна: S= d1xd2/8, поскольку в ромбе таких треугольников четыре, площадь ромба будет равняться: Sр= d1xd2/8×4= d1xd2/2 т.е. половине произведения его диагоналей.
Стрымбрым 8 лет назад Ромбом называют параллелограмм, у которого все стороны равны между собой. Частный случай ромба – квадрат (ромб с прямыми углами). А чтобы определить площадь ромба, требуется перемножить его диагонали и разделить пополам.
иришенька 8 лет назад Сделать это совсем несложно. Итак, если известны диагонали то их нужно просто перемножить, а затем разделить на 2. Думаю, теперь вы без труда сможете определить площадь ромба, зная только его диагонали. Знаете ответ? |
Площадь ромба через диагонали: онлайн-калькулятор
Найти площадь фигуры можно несколькими способами. Один из них – использовать в расчетах значения диагоналей. Калькулятор на нашем сайте доступен без регистрации. Пользователь может вводить значения без ограничений в количестве вычислений.
Сервис используют учащиеся школ и университетов, родители учеников, преподаватели. Также среди пользователей работники технических профессий, которым необходимо быстро произвести расчеты.
Формула площади ромба через диагонали
В автоматическом подсчете сначала единицы измерения переводятся в необходимые. Затем программа переходит к непосредственному решению.
Чтобы вычислить площадь ромба по диагоналям, следует произведение диагоналей разделить пополам:
S=12·d1·d2.
Сервис с калькуляторами создан для расширения возможностей получить качественное образование. Zaochnik позволяет:
- Сэкономить деньги на репетиторах. В разделе собраны все основные темы. С их помощью ученик может самостоятельно подготовиться к поступлению в ВУЗ.
- Не отставать от программы. Пропущенная тема легко отрабатывается на примерах. Пошаговое решение помогает запомнить алгоритм и применять его в дальнейшем.
- Быстро проверять выполненные задания. Родители и преподаватели теперь смогут тратить меньше времени на проверку домашних заданий.
- Не растеряться на контрольной. Если необходимо срочно вспомнить формулу и свериться с ответом, найдите нужный калькулятор, введите данные и получите вычисления с готовым ответом.
Если тема все равно осталась непонятной или срочно надо сделать объемное задание, напишите консультанту. Он подберет опытного преподавателя из нашего штата. По выгодной цене вы получите готовый к сдаче проект.

{S = a^2 cdot sin (alpha)}
На этой странице мы предлагаем вам 7 формул площади ромба. Для каждой формулы можно воспользоваться онлайн калькулятором и мгновенно получить результат, не прибегая к помощи обычного калькулятора
Содержание:
- калькулятор площади ромба
- формула площади ромба через сторону и угол
- формула площади ромба через сторону и высоту
- формула площади ромба через диагонали
- формула площади ромба через угол и диагональ из угла
- формула площади ромба через угол и противолежащую диагональ
- формула площади ромба ромба через радиус вписанной окружности и угол
- формула площади ромба через радиус вписанной окружности и сторону
- примеры задач
Формула площади ромба через сторону и угол

S = a^2 cdot sin (alpha)
a – сторона ромба
α – угол между сторонами ромба
Формула площади ромба через сторону и высоту

S = a cdot h
a – сторона ромба
h – высота ромба
Формула площади ромба через диагонали
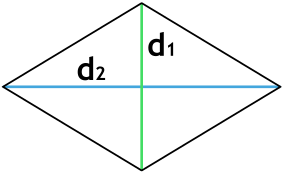
S = dfrac{d_1 cdot d_2}{2}
d1 и d2 – диагонали ромба
Формула площади ромба через угол и диагональ из угла
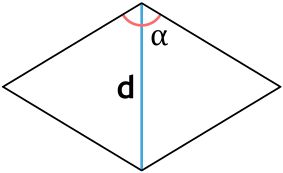
S = dfrac{d^2}{2} cdot \tg(dfrac{alpha}{2})
d – диагональ ромба
α – угол между сторонами ромба, из которого выходит диагональ
Формула площади ромба через угол и противолежащую диагональ

S = dfrac{d^2}{2} cdot ctg(dfrac{alpha}{2})
d – диагональ ромба, противоположная углу α
α – угол между сторонами ромба
Формула площади ромба через радиус вписанной окружности и угол
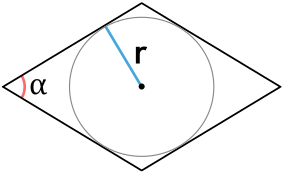
S = dfrac{4r^2}{sin(alpha)}
r – радиус окружности
α – угол между сторонами ромба
Формула площади ромба через радиус вписанной окружности и сторону
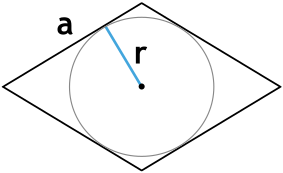
S = 2ar
r – радиус окружности
a – сторона ромба
Примеры задач на нахождение площади ромба
Задача 1
Найдите площадь ромба если его диагонали равны 34 и 4.
Решение
Для решения задачи воспользуемся формулой площади ромба через диагонали.
S = dfrac{d_1 cdot d_2}{2} = dfrac{34 cdot 4}{2} = 68 : см^2
Ответ: 68 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь ромба если его диагонали равны 4 и 6.
Решение
Задача аналогична предыдущей.
S = dfrac{d_1 cdot d_2}{2} = dfrac{4 cdot 6}{2} = 12 : см^2
Ответ: 12 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь ромба стороны которого равны 5, а высота равна 4.
Решение
Воспользуемся формулой площади ромба через высоту и сторону.
S = a cdot h = 5 cdot 4 = 20 : см^2
Ответ: 20 см²
Проверим полученный ответ на калькуляторе .
Как считать:
через сторону и высоту
через диагонали
через сторону и угол
Укажите размеры:
Результат:
Решение:
Ссылка на страницу с результатом:
# Теория
Ромб – это параллелограмм у которого все стороны равны.
Расчёты площади ромба основааны непосредственно на данных свойствах ромба:
- Все стороны ромба равны;
- Диагонали ромба пересекаются под прямым углом и в месте пересечения делятся пополам;
- Сумма углов, прилежащих к одной стороне ромба, равна 180°
- Противоположные углы ромба равны.
Формула площади ромба
Площадь ромба через сторону и высоту
a
a
a
a
h
S = a cdot h
- S – площадь ромба
- a – сторона ромба
- h – высота
Площадь ромба через диагонали
d
1
d
2
S = dfrac{d_1 cdot d_2}{2}
- S – площадь ромба
- d1 и d2 – диагонали ромба
Площадь ромба через сторону и угол
При расчёте площади ромба через сторону и угол, значение для α можно брать у любого угла – как устрого так и тупого (синус у них будет одиноковый).
S = a^2 cdot sin alpha
- S – площадь ромба
- a – сторона ромба
- sin α – синус угла
Похожие калькуляторы:
Войдите чтобы писать комментарии



