Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
![]()
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:

SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
![]()
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:

SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
![]()
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
![]()
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
![]()
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
 ACD
ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко

Профиль
Благодарили: 0
Сообщений: 1

Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?![]()
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев

Профиль
Благодарили: 0
Сообщений: 8

Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Формулы площади геометрических фигур
Площадь геометрической фигуры – численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника

-
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p – a)(p – b)(p – c)
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. -
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S – площадь треугольника,
a, b, c – длины сторон треугольника,
h – высота треугольника,
γ – угол между сторонами a и b,
r – радиус вписанной окружности,
R – радиус описанной окружности,p = a + b + c – полупериметр треугольника. 2
Формулы площади квадрата

-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S – площадь квадрата,
a – длина стороны квадрата,
d – длина диагонали квадрата.
Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S – Площадь прямоугольника,
a, b – длины сторон прямоугольника.
Формулы площади параллелограмма

-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S – Площадь параллелограмма,
a, b – длины сторон параллелограмма,
h – длина высоты параллелограмма,
d1, d2 – длины диагоналей параллелограмма,
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма.
Формулы площади ромба

-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.где S – Площадь ромба,
a – длина стороны ромба,
h – длина высоты ромба,
α – угол между сторонами ромба,
d1, d2 – длины диагоналей.
Формулы площади трапеции

-
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a – b| -
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S – площадь трапеции,
a, b – длины основ трапеции,
c, d – длины боковых сторон трапеции,p = a + b + c + d – полупериметр трапеции. 2
Формулы площади выпуклого четырехугольника

-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S – площадь четырехугольника,
d1, d2 – длины диагоналей четырехугольника,
α – угол между диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-

Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p – a)(p – b)(p – c)(p – d) – abcd cos2θ
где S – площадь четырехугольника,
a, b, c, d – длины сторон четырехугольника,
p = a + b + c + d2 – полупериметр четырехугольника,
θ = α + β2 – полусумма двух противоположных углов четырехугольника.
-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p – a)(p – b)(p – c)(p – d)
Формулы площади круга

-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S – Площадь круга,
r – длина радиуса круга,
d – длина диаметра круга.
Формулы площади эллипса
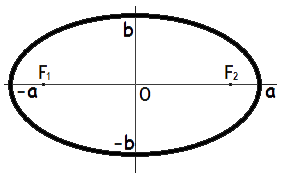
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S = π · a · b
где S – Площадь эллипса,
a – длина большей полуоси эллипса,
b – длина меньшей полуоси эллипса.
1. Формула площади равнобедренной трапеции через стороны и угол

b – верхнее основание
a – нижнее основание
c – равные боковые стороны
α – угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):



2. Формула площади равнобокой трапеции через радиус вписанной окружности

R – радиус вписанной окружности
D – диаметр вписанной окружности
O – центр вписанной окружности
H – высота трапеции
α, β – углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d – диагональ трапеции
α, β – углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m – средняя линия трапеции
c – боковая сторона
α, β – углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b – верхнее основание
a – нижнее основание
h – высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):

Площади фигур
Ученик – это факел, который надо зажечь.
Цели: познакомить и довести до понимания понятие «площадь фигуры», научить находить площадь фигур, используя различные приемы.
Задачи:
- Формирование у учащихся понимания площади как количества квадратов, размещенных на поверхности данной фигуры, и умения применять свойства площадей при их нахождении.
- .Знакомство с разнообразием плоских фигур и способами нахождения их площадей (использование палетки, миллиметровой бумаги, дополнение до прямоугольника, деление пополам перегибанием по диагонали).
- Развитие действий наблюдения, конструирования, измерений, восприятия геометрических конфигураций, выполнения графических действий, критического мышления и активности в получении знаний.
- Воспитание ответственности и толерантности к одноклассникам.
- Привитие навыков аккуратной работы с колюще-режущими инструментами (ножницы, линейки, карандаши).
- Развитие интереса к изучению математики, исторических фактов в ее развитии, известных и менее известных математиков.
План урока:
0) Перемена — Песня из м/Ф «38попугаев»(51сек.) Слайд №0
I. Рефлексия настроения (приглашение к сотрудничеству).
II. Формулировка темы урока.
1.Создание проблемной ситуации, м/ф «38 попугаев» (2мин. 15сек.)
2.Обсуждение возникшей проблемы (1,2)
3.Исторические сведения в ее решении (1870, Париж, 24, эталоны)
4.Формулировка темы урока.
III. Новый материал.
1.Выбор единицы измерения площади (мерки-квадраты)
2.Объяснение понятия площади на примере. Cлайд №1
3.Обучающие практические работы:
№1) S учебника — укладка квадратов. Слайд №2,3
№2) S парты по формуле. Слайд №4,5,6
№3) S квадрата рисунок с учебника. Слайд №7,8,9
№4) в прямоугольнике диагональ ─ 2 равных треугольника. S треугольника. Слайд №10,11
№ 5) Фигуру треугольника достраиваем до прямоугольника.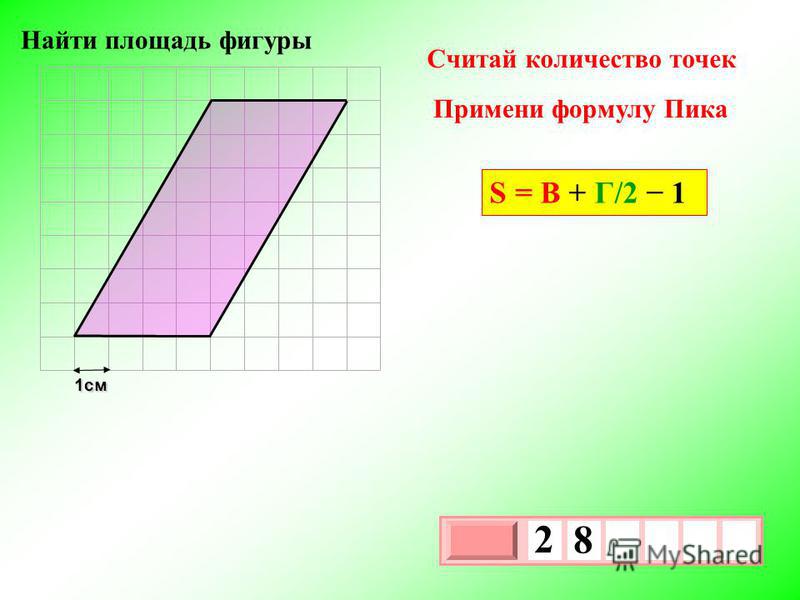
Слайд №12
Вырезать этот прямоугольник, потом фигуру треугольника, остатки наложить на фигуру треугольника. (=)
Фигуры равны = площади равны, а обратно???
№ 6) S фигур одинаковые, но фигуры неравны. Слайд №13;14
а) 2 равных квадрата; 1делим на 4 квадрата, 2 квадрата делим на 2 треугольника
б) из частей собираем треугольник
IV. Закрепление нового. Решение устных задач по готовым рисункам.
Слайд №15. 1) Сравнение периметров и площадей ( Р1=Р2, S1>S2)
Слайд №16. 2) Сравнение периметров и площадей (Р1>Р2, S1<S2)
Слайд №17. 3) Сравнение периметров и площадей (Р1>Р2, S1=S2)
4) Возможно использование палетки, миллиметровки (просто к сведению)
V. Проверка усвоения нового. Обсуждение, чтение с доски выводов.
VI. Подведение итогов. Благодарю за активное сотрудничество. Изучение формул для нахождения площадей других фигур на следующих уроках.
VII. Рефлексия настроения.
Ход урока
Песня из м/ф «38 попугаев»
I.
Приветствую учеников.
II.
1. Просмотр мультфильма «38 попугаев».
2.
а) В чем состоит процесс измерения длины удава?
б) Почему длина одного удава выражается разными числами?
1 удав=2 слона=5 мартышек=38 попугаев. Как понять — много это или мало?
в) Как избежать ситуации, что длина одного предмета различна?
Нужно договориться о мерках. Чем измерять длину?
3. Слоны, мартышки, попугаи… Как в м/ф многообразие единиц измерения привело к неудобствам?
Так и в жизни людей при обменах, куплях-продажах, строительстве шаги, локти, дюймы, сажени, мили, акры и аршины… тормозили развитие производства и сельского хозяйства.
Передовые ученые разных стран начали активную агитацию за установление единых мер во всем.
В 1870 году в Париже собрались представители 24 стран, утвердили эталон длины ─ 1 метр, который изготовлен из сплава платины (90%) и иридия (10%), а эталон веса ─1 килограмм, вес 1 дм3 (литра) воды при температуре 4 С.
Комиссия постановила изготовить копии эталонов и распределить между странами заказчиками.
С этого времени в музеях разных стран хранятся эталоны метра и килограмма и делаются их многочисленные точные копии для использования на производстве, в хозяйстве, в повседневной жизни людей, включая нас с вами.
Предлагаю вам почитать об этом времени, как это происходило, найти как можно больше названий разных мер (длины, площади, времени, денежных единиц). Это будет вашим домашним заданием. А сегодня мы согласно теме урока поведем разговор о площади фигур.
Запись темы урока в тетради: Площадь фигур.
III. Новый материал
1. Выбор единицы измерения площади.
Как мы поняли из м/ф надо договориться о мерке, о единице измерения. Чем будем измерять площадь?
1) Запись в тетради: Единица измерения площади фигур (мерка площади) — квадрат, сторона которого равна единице измерения длины:
если сторона квадрата 1 м, значит, площадь его 1 м²;
если сторона квадрата 1 дм, значит, площадь его 1 дм²;
если сторона квадрата 1 см, значит, площадь его 1 см²;
если сторона квадрата 1 мм, значит, площадь его 1 мм²;
2) Единицы измерения ─ 1 м
²; 1 дм²; 1 см²; 1 мм².
Крупные площади измеряются большими единицами измерения:
1км², 1сотка = 1ар = 100м², 1га = 100ар = 10000 м²
Найдите на столе 3 квадрата красного цвета – это мерки, которыми мы будем пользоваться.
Измерьте сторону самого большого красного квадрата, для этого положите линейку так, чтобы «0» на линейке совпал с левым углом квадрата, линейку совместите со стороной квадрата, правый угол квадрата указывает на какое число? 10 см = 1 дм. Это, значит, длина стороны равна 10 см (1 дм) А чему равна площадь? S = 1 дм² (=100 см²). Подпишем мерку №1.
Измерьте сторону среднего квадрата так же, совместив левый угол квадрата с «0» на линейке, а правый угол укажет на число «1». Длина стороны среднего квадрата 1см (10мм). А чему равна площадь его? S=1 см² (=100 мм²). Подпишем мерку №2.
Измерьте сторону самого маленького квадрата. Длина стороны 1 мм. А чему равна его площадь? S = 1 мм². Мерка №3.
2. Рассмотрим фигуру на рисунке.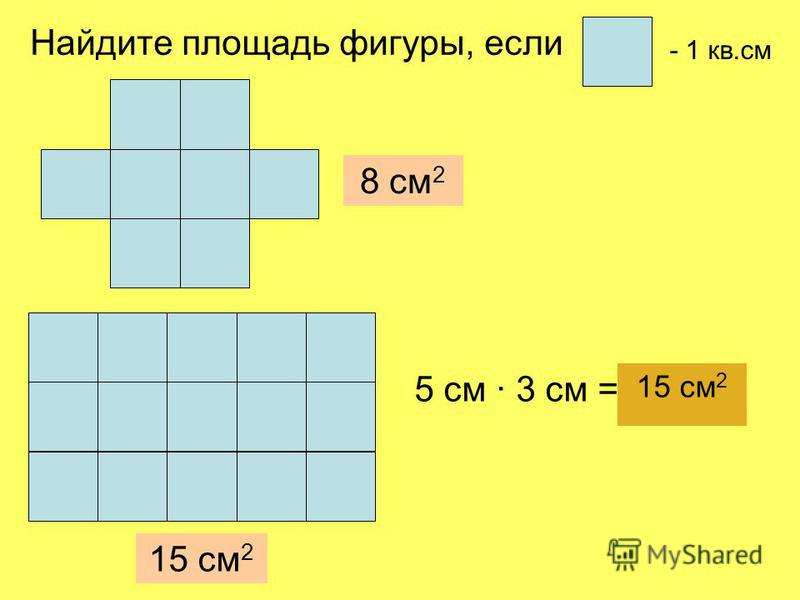 Слайд №1
Слайд №1
Что же такое площадь фигуры?
3) Запись в тетради: Площадь фигуры – это количество квадратов, которое можно уместить на поверхности фигуры.
Обучающие практические работы:
№1) Нахождение площади учебника (прямоугольника).
Выберите подходящий квадрат-мерку. Сколько раз укладывается на поверх- ности данного прямоугольника? Значит, какова площадь прямоугольника? А что такое площадь? А как вы считали? Было удобно? Размеры учебника 16, 21. Слайд №2,3
№2) Нахождение площади парты (прямоугольника).
Выберите подходящий квадрат-мерку, которым будем измерять. Мерка сколько раз укладывается на поверхности данного прямоугольника? Значит,
какова площадь прямоугольника? А что такое площадь? А как вы считали? Было удобно? А кто работал по-другому?
Можно ли было укладывать на этот прямоугольник мерки большего размера?
Нахождение площади прямоугольника можно считать укладыванием квадратов-мерок, а можно умножить длину на ширину, это формула нахождения площади прямоугольника.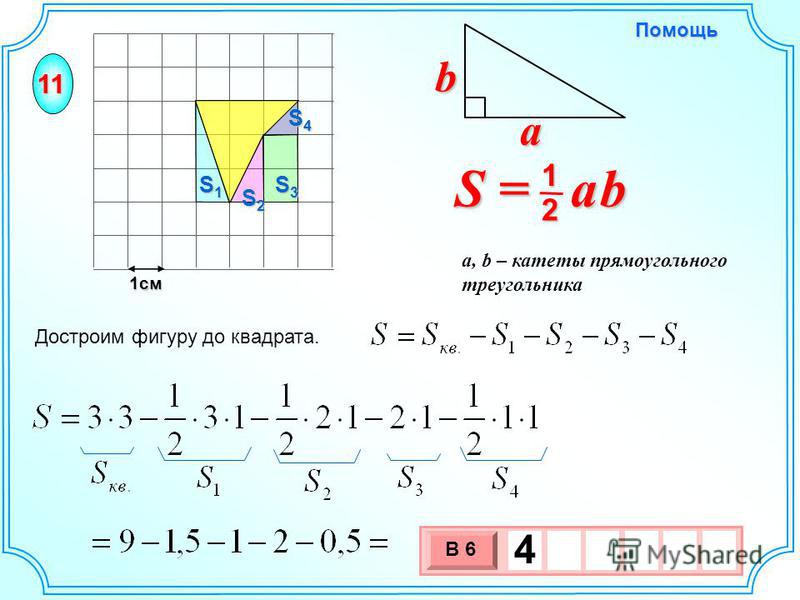
4) Запись в тетради: Прямоугольник S=ab, где a, b – длина, ширина.
№3) Нахождение площади квадрата, изображённого на корочке учебника «Геометрия 7-9». Выясняем, кто пользовался наложением, а кто формулой. Длина стороны квадрата 6см, значит S=36см² Слайд №4,5,6
4) Запись в тетради: Квадрат
S=a²
№4) Находим площадь треугольника. Слайд №7,8,9
5) Запись в тетрадь: Равные фигуры имеют равные площади.
а) Прямоугольник на плотной бумаге (зелень). Найдите площадь прямоугольника:
S=5 · 3=15см², запомните.
б) Разрежьте прямоугольник — зелень по диагонали. Проверьте, наложением,
полученные части треугольники — зелень равны?
в) Треугольники равны, значит, площади равны. S=15:2=7,5см2.
S=15:2=7,5см2.
Площадь треугольника равна половине площади прямоугольника.
6) Запись в тетради: Треугольник S=ab/2
Здесь мы воспользовались ещё важным свойством,
7) Запись в тетради: Если фигура состоит из частей, то площадь фигуры равна сумме площадей.
Слайд №10,11
№5). Найдите произвольный треугольник-лимон,
а) Достройте его до прямоугольника. Слайд №12
б) Найди площадь прямоугольника.
в) Теперь площадь треугольника, для этого разделим площадь прямоугольника на 2.
г) Убедитесь наложением, что оставшиеся части вместе составляют треугольник-лимон, т.е. площадь треугольника равна половине площади достроенного прямоугольника.
Фигуры равны = площади равны, а обратно???
№6)
а) Вырежем 2 квадрата-шоколада, для этого вам придётся объединиться, т.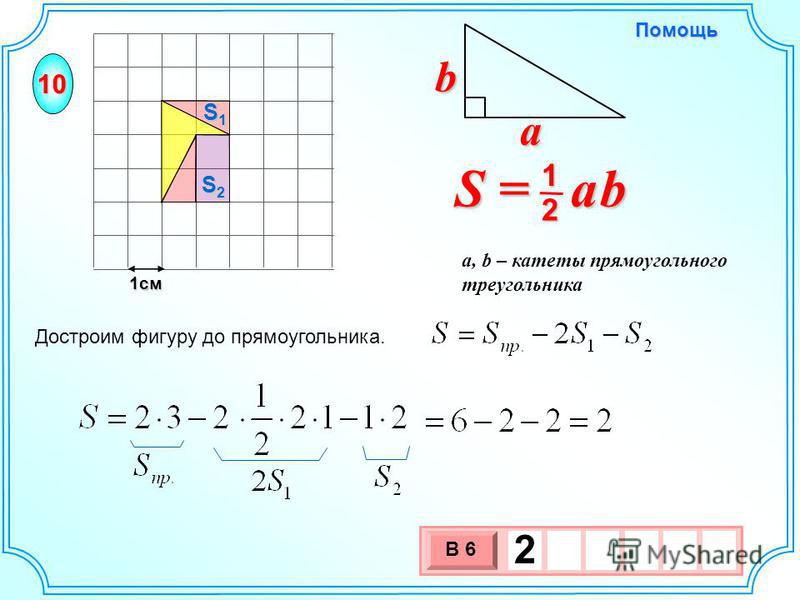 к. в наборе один шоколадный лист, длину отрежьте как ширину.
к. в наборе один шоколадный лист, длину отрежьте как ширину.
б) Один из 2 одинаковых квадратов-шоколадов, разделим на 4 одинаковых квадрата, 2 квадрата оставим, а другие 2разделим по диагонали на 2 треугольника. Слайд №13,14
в) Большой треугольник-шоколад составьте из частей, на которые разделен квадрат.
Сравни площади большого квадрата и большого треугольника.
8) Запись в тетради: Фигуры неравные, но составлены из одинаковых частей, значит, площади равны. Равновеликие.
IV. Закрепление нового материала
Решение задач по рисунку (устно). Слайд №15
1) Сравни периметры фигур самым легким способом. Сравни площади фигур. Сделай вывод. В чем отличие линий 1 и 2 фигур? А длина этих линий разная или одинаковая?
9) Запись в тетради: Периметры фигур равны, а площади не равны.
2) Слайд №16
Сравни периметры фигур самым легким способом. Сравни площади фигур.
| Периметр: вертик.14+горизонт.14=28 |
Периметр: вертик.12+горизонт.10=22 |
В чем отличие линий? Сколько горизонтальных? Сколько вертикальных?
Площади: S1=17 клеток, S2=18 клеток.
Вывод: Периметр фигуры больше, но ее площадь меньше.
3) Слайд №17
Сравни периметры фигур самым легким способом. Сравни площади фигур. Сделай вывод.
Вывод: Квадрат, имея меньший периметр, имеет площадь равную площади
прямоугольника с большим периметром.
Запись в тетрадь: Садовый участок квадратной формы выгоднее, экономия на заборе.
Более вытянутая фигура имеет меньшую площадь, чем более компактная при одинаковом периметре.
4) Иногда используют для нахождения площадей палетку (прозрачная пленка,
разделенная на одинаковые квадраты). Чтобы узнать площадь фигуры сначала
считают сколько полных квадратов. Потом сколько неполных квадратов.
Договорились два неполных квадрата считать за один.
V. Проверка усвоения нового материала
1) Что такое площадь? (Площадь – количество квадратов, занимаемых фигурой.)
2) Удобнее вычислять площадь по формулам или использовать наложение?
3) Формула площади прямоугольника S=a b.
4) Формула площади треугольника S=½ a b.
5) Равные фигуры имеют равные площади.
6) Фигуры, составленные из равных частей, имеют одинаковую площадь.
7) Садовый участок – квадрат выгоднее прямоугольника.
VI. Подведение итогов
Благодарю за активное сотрудничество. Изучение формул для нахождения площадей других фигур на следующих уроках.
Изучение формул для нахождения площадей других фигур на следующих уроках.
VII. Рефлексия настроения
Шуточное стихотворение:
— Эх, — вздыхали рыбаки,
— Это разве судаки?
Раньше вытащишь рыбеху,
— Хвост, бывало, в полруки!
— Эх, вздыхали судаки,
— Раньше были червяки…
Червяком одним, бывало,
— Наедалось полреки!
— Эх, — вздыхали червяки,
— Раньше врали рыбаки!
Мы, послушав их, бывало,
Сами лезли на крючки!
Запись на доске (и в тетради)
Площадь фигур
1) Единица измерения площади фигур (мерка площади) — квадрат, сторона
которого равна единице измерения длины:
1м²; 1дм²; 1см²; 1мм²; 1м2; 1дм²; 1см²; 1мм².
1км², 1сотка=1ар=100м², 1га=100ар=10000м²
2) Площадь фигуры – это количество квадратов, которое можно уместить на поверхности фигуры.
3) Прямоугольник S=a b, где a, b – длина, ширина.
4) Квадрат S=a².
5) Равные фигуры имеют равные площади.
6) Треугольник S=ab/2.
7) Если фигура состоит из частей, то площадь фигуры равна сумме площадей.
8) Фигуры неравные, но составлены из одинаковых частей, значит, площади равны. Равновеликие.
9) Cадовый участок квадратной формы выгоднее, чем прямоугольной (экономия на заборе).
Площади геометрических фигур / math5school.ru — Общие дети, г. Воронеж
Площадь кругового кольца равна четверти произведения числа «пи» на разность квадратов внешнего и внутреннего диаметров.2cdot text{ctg}(frac{pi}{n})$
n — число ребер(вершин).
$pi=3,14159265359$
Площадь геометрической фигуры
Что такое площадь
Площадь геометрической фигуры — это неотрицательная численная величина, которая характеризует размер этой фигуры.
Изначально, геометрия в Древней Греции (по-гречески «землемерие») занималась измерением площадей и объемов. Значительное число задач в области элементарной геометрии посвящено именно таким вопросам.
Значительное число задач в области элементарной геометрии посвящено именно таким вопросам.
Общим методом нахождения площадей фигур в координатной плоскости является интегральное исчисление. Этими вопросами занимается математический анализ.
Для понимания применения универсального метода математического анализа для определения площади фигур можно привести следующие примеры вычисления площади:
- Площадь фигуры, заключенная между графиком непрерывной функции на интервале [a,b] и осью абсцисс, равна определенному интегралу этой функции на том же интервале
- Площадь фигуры, заключенная между графиками двух непрерывных функций на интервале [a,b] равна разности определенных интегралов этих функций на этом интервале
Или, с помощью формул это будет выглядеть следующим образом:
Как видно из рисунка и из формул, площадь фигуры, заключенной между графиком непрерывной функции f(x) и осью координат x на интервале [a,b] равна определенному интегралу этой функции [1].
Если же нам необходимо найти площадь фигуры, заключенной между графиками двух непрерывных функций — мы просто находим определенный интеграл для обоих функций и вычитаем площадь одной фигуры из площади другой. Разность площадей и даст нам искомую величину.
С помощью интегрального исчисления также определяются площади поверхностей фигур и в полярных координатах (фигура, заключенная между двумя лучами) и в трехмерном пространстве.
Свойства площади фигур
Площадь фигуры – это неотрицательная величина, числовое значение которой имеет следующие свойства:
- Площадь фигуры является неотрицательной величиной
- Равные фигуры имеют равные площади
- Площадь фигуры равна сумме составляющих ее и не перекрывающих друг друга частей (свойство аддитивности).
- Площадь квадрата со стороной, равной единице измерения, равна единице (свойство нормированности)
- Площадь фигуры всегда больше площади ее части (свойство монотонности)
Формулы для нахождения площадей геометрических фигур
Площадь квадрата со стороной а
S=a2
См. также — квадрат и площадь квадрата. Все формулы.
также — квадрат и площадь квадрата. Все формулы.
Площадь прямоугольника со сторонами а и b
S=ab
См. также Задачи про нахождение площади прямоугольника с пояснениями.
Площадь параллелограмма со сторонами а и b или с основанием а и высотой h
S=ah
S=ab*sin ∠ab
См. также свойства и площадь параллелограмма.
Площадь ромба со стороной а, углом между сторонами α, диагоналями d1, d2
S=ab*sinα
или
S=1/2 d1d2
См. также Задачи о ромбе.
также Задачи о ромбе.
Площадь треугольника с основанием а и высотой h
S=1/2 ah
См. также площадь треугольника (все формулы).
Площадь трапеции с основанием а, b и высотой h
S=(a+b)/2 * h
См. также свойства и площадь трапеции (все формулы).
Площадь круга
S=πR2
См. также Задачи про окружность.
Биссектриса. Примеры решения задач |
Описание курса
| Окружность. Уравнение окружности
Как найти площадь геометрических фигур?boeffblog.
 ru
ru
Что такое площадь?
Площадь – характеристика замкнутой геометрической фигуры (круг, квадрат, треугольник и т.д.), которая показывает ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Обозначается буквой S (square).
Как найти площадь треугольника?
1. Самая известная формула площади треугольника по стороне и высоте:
S = a · h
где a – длина основания, h – высота треугольника, проведенная к основанию.
Причем, основание не обязательно должно находиться снизу. Так тоже сойдет.
Если треугольник тупоугольный, то высота опускается на продолжение основания:
Если треугольник прямоугольный, то основанием и высотой являются его катеты:
2. Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:
S = a · b · sinα
где a и b – две стороны треугольника, sinα – синус угла между этими сторонами.

Главное условие – угол берется между двумя известными сторонами.
3. Формула площади по трем сторонам (формула Герона):
S =
где a, b и с – стороны треугольника, а р – полупериметр. p = (a + b + c)/2.
4. Формула площади треугольника через радиус описанной окружности:
S =
где a, b и с – стороны треугольника, а R – радиус описанной окружности.
5. Формула площади треугольника через радиус вписанной окружности:
S =p · r
где р – полупериметр треугольника, а r – радиус вписанной окружности.
Как найти площадь прямоугольника?
1. Площадь прямоугольника находится довольно-таки просто:
Площадь прямоугольника находится довольно-таки просто:
S = a · b
Никаких подвохов.
Как найти площадь квадрата?
1. Так как квадрат является прямоугольником, у которого все стороны равны, то к нему применяется такая же формула:
S = a · a = a2
2. Также площадь квадрата можно найти через его диагональ:
S = d2
Как найти площадь параллелограмма?
1. Площадь параллелограмма находится по формуле:
S = a · h
Это связано с тем, что если от него отрезать прямоугольный треугольник справа и приставить его слева, получится прямоугольник:
2. Также площадь параллелограмма можно найти через угол между двумя сторонами:
Также площадь параллелограмма можно найти через угол между двумя сторонами:
S = a · b · sinα
Как найти площадь ромба?
Ромб по своей сути является параллелограммом, у которого все стороны равны. Поэтому для него применяются те же формулы площади.
1. Площадь ромба через высоту:
S = a · h
2. Площадь ромба через угол между сторонами:
S = a · a sinα = a2 · sinα
3. Площадь ромба через диагонали:
Площадь ромба через диагонали:
S = d1 · d2
Как найти площадь трапеции?
1. Площадь трапеции находится по следующей формуле:
S = · h
Как найти площадь круга?
1. Площадь круга можно найти через радиус:
S = π r2
2. Площадь круга можно найти через диаметр:
S = πd2/4
Площадь | интернет проект BeginnerSchool.ru
В этой статье мы разберемся, как вычислить площадь фигуры.
Сравнить площади разных фигур можно способом наложения. Посмотрите на рисунок. Мы видим две фигуры: треугольник и прямоугольник. Для того, чтобы их сравнить мы можем наложить меньшую фигуру на большую. Треугольник полностью поместился в прямоугольнике, это значит, что треугольник меньше прямоугольника.
Посмотрите на рисунок. Мы видим две фигуры: треугольник и прямоугольник. Для того, чтобы их сравнить мы можем наложить меньшую фигуру на большую. Треугольник полностью поместился в прямоугольнике, это значит, что треугольник меньше прямоугольника.
Но не всегда можно сравнить площади фигур таким способом. Тогда можно разбить фигуру на равные квадраты и посчитать количество квадратов входящих в эту фигуру.
На рисунке изображено две фигуры. Путем наложения эти фигуры сравнить невозможно. Мы разбили эти фигуры на квадраты с одинаковой площадью. Теперь можно посчитать количество квадратов входящих в эти фигуры. В первую фигуру вписалось 6 квадратов, а во вторую 8. Значит площадь первой фигуры меньше площади второй.
Площадь фигуры равна числу единичных квадратов, составляющих эту фигуру.
Если у квадрата сторона равна 1 см, то площадь такого квадрата равна 1 квадратному сантиметру (см2).
Площадь квадрата сторона которого равна 1 дециметр равна 1 квадратному дециметру (дм2) или 100 квадратным сантиметрам(см2).
Площадь фигуры обозначается заглавной латинской буквой S.
Допустим нам надо найти площадь прямоугольника, длины сторон которого равны 6 и 4 см. Разделим прямоугольник на квадратные сантиметры и вычислим его площадь.
Итак, умножим длину прямоугольника на его ширину и получим площадь:
S = 6 × 4 = 24 см2
Чтобы вычислить площадь прямоугольника, надо измерить его длину и ширину в одинаковых единицах измерения и найти их произведение.
Если известна площадь прямоугольника и ширина, то найти длину просто, надо разделить площадь на известную длину.
Д = S ÷ Ш
или
Ш = S ÷ Д
Например, площадь прямоугольника равна 15 см2. Длина прямоугольника равна 5 см. Найдем его ширину:
Ш = 15 ÷ 5 = 3 см
Если фигура сложная, например, такая как на рисунке, то вычислить её площадь можно разбив фигуру на прямоугольники, вычислить их площадь, а затем сложить полученные площади.
Итак нашу фигуру мы можем разбить на два прямоугольника: первый площадью 2 см2, и второй площадью 8 см2:
S = 2 × 1 + 4 × 2 = 10 см2
А как найти площадь прямоугольного треугольника. Для этого надо достроить треугольник до прямоугольника, так как показано на рисунке.
Для этого надо достроить треугольник до прямоугольника, так как показано на рисунке.
Теперь найдем площадь полученного прямоугольника и разделим её пополам:
S = (3 × 6) ÷ 2 = 9 см2
Кажется все просто, когда треугольник прямоугольный. Если у треугольника нет прямого угла, то вычислить его площадь можно следующим образом:
На следующем рисунке мы видим треугольник, площадь которого нам надо вычислить, он выделен желтым цветом. Впишем его в прямоугольник, так как показано на рисунке. Длина полученного прямоугольна – 5 см. Ширина – 4 см. Вершина треугольника делит длину прямоугольника на части в 3 и 2 см.
Теперь для того, чтобы найти площадь нашего треугольника, надо вычислить площади двух полученных прямоугольных треугольников и сложить их:
S1 = (3 × 4) ÷ 2 = 6 см2
S2 = (2 × 4) ÷ 2 = 4 см2
S = S1 + S2 = 6 + 4 = 10 см2
Спасибо, что Вы с нами.
Понравилась статья — поделитесь с друзьями:
Оставляйте пожалуйста комментарии в форме ниже
Площади фигур.
 Сравнение площадей фигур
Сравнение площадей фигур
Планируемые результаты:
- Личностные: формировать понимание значения математических знаний в жизни и деятельности людей, осознание личностного смысла изучения математики, укреплять интерес к изучению математики;
- Познавательные: находить нужную информацию в различных источниках, устанавливать математические отношения между объектами (геометрические фигуры), рассуждать, делать выводы и фиксировать их, решать задачи практического содержания;
- Метапредметные: формировать умения планировать, контролировать и оценивать учебные действия; овладение логическими действиями сравнения, анализа, синтеза;
- Предметные: знакомство с понятием «Площадь», формировать умения сравнивать площади фигур тремя способами.
Тип урока: урок открытия нового знания.
Ход урока
1. Активизация внимания, актуализация знаний
1 слайд.
— Назовите данные предметы. (Плоские геометрические фигуры)
— Какое задание предлагаете выполнить? (разделить на группы, найти Р)
— Как найти периметр? Найдите периметр, сравните их.
Как вы считаете, можно ли ещё как то сравнить плоские фигуры? (ответы ребят)
2. Введение в новую тему
Над чем будем работать на уроке? Определите тему урока.
На доске.
Тема. Площади фигур. Сравнение площадей фигур.
— Какие вопросы возникают к данной теме? (вопросы ребят)
— Н а основании ваших вопросов поставим цели для себя на урок.
Цели.
- Узнать что такое площадь.
- Учиться сравнивать площади разных фигур.
3. Работа по теме урока
а) Где в жизни вы встречались со словом площадь? Как вы можете сказать, что такое площадь? Как вы понимаете площадь фигуры?
б) работа со словарями в группах.
Найти в словарях определение площади и прочитать. (читают)
Слайд 2, 3 (написаны три определения площади)
Какое определение соответствует нашему уроку? Почему?
в) практическая работа
Вырежите любую фигуру. Закрасте цветным карандашом площадь вашей фигуры.
(работа в группе) Покажите площадь вашей фигуры и замкнутую линию, которая ограничивает площадь фигуры.
Вывод. Что называется площадью фигуры? (обязательно вернуться к первой цели урока)
-Достигли первой цели? Какую ещё цель мы перед собой поставили?
г) способы сравнения площадей фигур.
Слайд 4. (два домика разные по цвету, размеру, но одинаковые по форме).
Из каких фигур состоят дома? Сравните площади домов. Как вы это сделали? (НА ГЛАЗ)
На доске. Способы сравнения площадей фигур.
1. На глаз.
На глаз.
— Найдите предметы в классе, площади которых вы можете сравнить на глаз.
(работа в группе с геометрическими фигурами) расположить фигуры в порядке возрастания их площадей, записать в таком порядке номера.
Самопроверка (ключ на доске)
Вывод. Как можно сравнить площади фигур? (на глаз)
— Я вам предлагаю сравнить площади ваших ладошек.
Найдите себе пару и сравните площади ладошек. (у детей возникают затруднения, но они находят способ наложения)
Поднимите руку у кого площадь ладошки больше. Хлопните в ладоши у кого площадь ладошки меньше. Возьмитесь за руки у кого площади ладошек одинаковые. (присаживаются на свои места)
— Как вы сравнивали площади ладошек.
— Как вы бы назвали этот способ? (дети высказываются)
2. Путём наложения. (добавить к способам сравнения площадей)
Используя данный способ сравните площади вашей тетради и учебника. (работа в паре)
-У каких предметов, которые находятся на вашей парте, мы можем сравнить площади путём наложения?
Вывод. Назовите второй способ сравнения фигур?
Назовите второй способ сравнения фигур?
Всегда ли эффективно использовать данные способы сравнения? Как вы считаете?
У вас на парте квадрат и прямоугольник. (Вырезаны из тетрадного листа в клеточку) Сравните их площади. (Способы на глаз и путём наложения учащиеся понимают что не подходят, находят новый способ)
Проверка у доски. 4∙ 4=16 клеточек, 8 ∙ 2 = 16 клеточек
Вывод. Как ещё можно сравнить площади фигур? (при помощи мерки)
3. При помощи мерки (добавить в способы сравнения площадей фигур)
4. Закрепление
Выполнить задание № 2., с.19 (работа в паре), используют третий способ, заполняют таблицу.
Взаимопроверка в группе по часовой стрелке. Ключ на доске.
Вывод. Разные фигуры по форме могут иметь одинаковую площадь.
5. Рефлексия
Тест. (проверка со слайда)
Вернуться к целям урока.
— Кто считает, что достиг целей урока, встаньте, пожалуйста. Кто считает, что ему ещё нужно поработать над данной темой, поднимите руку.
— Где в жизни нам пригодиться материал урока?
Дз. На выбор из рабочей тетради.
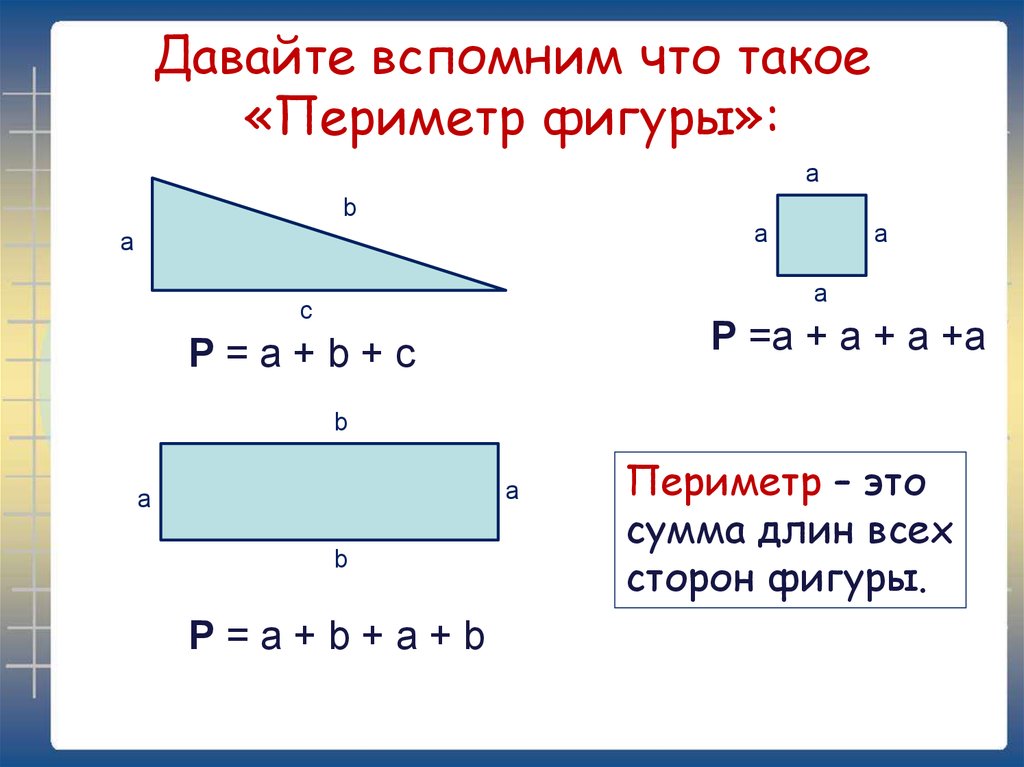
Периметр и площадь геометрических фигур
Существует много плоских геометрических фигур: точка, линия (прямая или кривая), отрезок, угол, ломаная и т. д.:
Если внимательно посмотреть на все эти фигуры, то можно выделить две из них, которые образованы замкнутыми линиями (окружность и треугольник). Эти фигуры имеют своего рода границу, отделяющую то что находится внутри, от того что находится снаружи. То есть граница делит плоскость на две части: внутреннюю и внешнюю область относительно фигуры, к которой она относится:
Периметр
Периметр – это замкнутая граница плоской геометрической фигуры, отделяющая её внутреннюю область от внешней.
Периметр есть у любой замкнутой геометрической фигуры:
На рисунке периметры выделены красной линией. Обратите внимание, что периметр окружности часто называют длиной.
Обратите внимание, что периметр окружности часто называют длиной.
Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.
У всех многоугольников нахождение периметра сводится к сложению длин всех сторон, то есть периметр многоугольника всегда равен сумме длин его сторон. При вычислении периметр часто обозначают большой латинской буквой P
:
Площадь
Площадь – это часть плоскости, занимаемая замкнутой плоской геометрической фигурой.
Любая плоская замкнутая геометрическая фигура имеет определённую площадь. На чертежах площадью геометрических фигур является внутренняя область, то есть та часть плоскости, которая находится внутри периметра.
Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Обычно за единицу измерения площади принимается квадрат, у которого сторона равна единице измерения длины: миллиметру, сантиметру, метру и т. д.
д.
На рисунке изображён квадратный сантиметр. Квадратный сантиметр — квадрат, у которого каждая сторона имеет длину 1 см:
Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д.
Таблица перевода квадратных единиц
мм2
см2
дм2
м2
ар (сотка)
гектар (га)
км2
мм2
1 мм2
0,01 см2
10-4 дм2
10-6 м2
10-8 ар
10-10 га
10-12 км2
см2
100 мм2
1 см2
0,01 дм2
10-4 м2
10-6 ар
10-8 га
10-10 км2
дм2
104 мм2
100 см2
1 дм2
0,01 м2
10-4 ар
10-6 га
10-8 км2
м2
106 мм2
104 см2
100 дм2
1 м2
0,01 ар
10-4 га
10-6 км2
ар
108 мм2
106 см2
104 дм2
100 м2
1 ар
0,01 га
10-4 км2
га
1010 мм2
108 см2
106 дм2
104 м2
100 ар
1 га
0,01 км2
км2
1012 мм2
1010 см2
108 дм2
106 м2
104 ар
100 га
1 км2
104 = 10 000
10-4 = 0,000 1
106 = 1 000 000
10-6 = 0,000 001
108 = 100 000 000
10-8 = 0,000 000 01
1010 = 10 000 000 000
10-10 = 0,000 000 000 1
1012 = 1 000 000 000 000
10-12 = 0,000 000 000 001
Площадь круга, треугольника, квадрата, прямоугольника, параллелограмма, трапеции, эллипса и сектора
Площадь — это размер поверхности!
Узнайте больше о площади или воспользуйтесь калькулятором площади.
Пример: Какова площадь этого прямоугольника?
Формула:
Площадь = w × h
w = ширина
h = высота
Мы знаем, что w = 5 и h = 3 , поэтому:
Площадь = 5 × 3 = 15
Пример: Какова площадь этого круга?
Радиус = r = 3
Площадь
= π × r 2
= π × 3 2
= π × (3 × 3)
= 3.14159 … × 9
= 28,27 (до 2 знаков после запятой)
Пример: Какова площадь этого треугольника?
Высота = h = 12
База = b = 20
Площадь = ½ × b × h = ½ × 20 × 12 = 120
Более сложный пример:
Пример: Сэм косит траву по цене 0,10 доллара за квадратный метр
Сколько зарабатывает Сэм, обрабатывая эту область:
Разобьем область на две части:
Часть А представляет собой квадрат:
Площадь A = a 2 = 20 м × 20 м = 400 м 2
Часть B представляет собой треугольник. При взгляде сбоку он имеет основание 20 м и высоту 14 м.
При взгляде сбоку он имеет основание 20 м и высоту 14 м.
Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2
Итак, общая площадь:
Площадь = Площадь A + Площадь B = 400 м 2 + 140 м 2 = 540 м 2
Сэм зарабатывает 0,10 доллара за квадратный метр
Сэм зарабатывает = 0,10 доллара × 540 млн 2 = 54 доллара
Калькулятор площади
. Найдите область из 16 популярных фигур!
Если вам интересно, как рассчитать площадь любой базовой формы, вы попали в нужное место — этот калькулятор площади ответит на все ваши вопросы.Воспользуйтесь нашим интуитивно понятным инструментом, чтобы выбрать из шестнадцати различных форм и вычислить их площадь в мгновение ока. Если вы ищете определение площади или, например, формулу ромба, у нас есть все необходимое. Продолжайте прокручивать, чтобы узнать больше, или просто поиграйте с нашим инструментом — вы не будете разочарованы!
Что такое площадь в математике? Определение площади
Проще говоря, площадь — это размер поверхности . Другими словами, его можно определить как пространство, занимаемое плоской формой.Чтобы понять концепцию, обычно полезно рассматривать площадь как как количество краски, необходимое для покрытия поверхности . Посмотрите на картинку ниже — все фигуры имеют одинаковую площадь, 12 квадратных единиц:
Другими словами, его можно определить как пространство, занимаемое плоской формой.Чтобы понять концепцию, обычно полезно рассматривать площадь как как количество краски, необходимое для покрытия поверхности . Посмотрите на картинку ниже — все фигуры имеют одинаковую площадь, 12 квадратных единиц:
Есть много полезных формул для вычисления площади простых форм. В разделах ниже вы найдете не только хорошо известные формулы для треугольников, прямоугольников и кругов, но и другие формы, такие как параллелограммы, воздушные змеи или кольца.
Мы надеемся, что после этого объяснения у вас не возникнет проблем с определением области в математике!
Как рассчитать площадь?
Ну конечно это зависит от формы ! Ниже вы найдете формулы для всех шестнадцати форм, представленных в нашем калькуляторе площади.Для ясности мы перечислим только уравнения — их изображения, объяснения и выводы можно найти в отдельных абзацах ниже (а также в инструментах, посвященных каждой конкретной форме).
Вы готовы? Вот наиболее важные и полезные формулы площади для шестнадцати геометрических фигур:
- Квадрат формула площади:
A = a²
- Прямоугольник формула площади:
A = a * b
- Формулы площади треугольника :
-
A = b * h / 2 или
-
А = 0.5 * a * b * sin (γ) или
-
A = 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)) или
-
A = a² * sin (β) * sin (γ) / (2 * sin (β + γ))
- Круг формула площади:
A = πr²
- Сектор круга формула площади:
A = r² * угол / 2
- Эллипс формула площади:
A = a * b * π
- Трапеция формула площади:
A = (a + b) * h / 2
- Параллелограмм формулы площади:
-
A = a * h или
-
A = a * b * sin (угол) или
-
A = e * f * sin (угол)
- Ромб формулы площади:
-
A = a * h или
-
A = (e * f) / 2 или
-
A = s² * sin (угол)
- Kite формулы площади:
-
A = (e * f) / 2 или
-
A = a * b * sin (γ)
- Пентагон Формула площади:
A = a² * √ (25 + 10√5) / 4
- Шестиугольник формула площади:
A = 3/2 * √3 * a²
- Восьмиугольник формула площади:
A = 2 * (1 + √2) * a²
- Кольцевое пространство формула площади:
A = π (R² - r²)
- Четырехугольник формула площади:
A = e * f * sin (угол)
- Правильный многоугольник формула площади:
A = n * a² * детская кроватка (π / n) / 4
Если ваша форма неправильная, попробуйте мысленно разделить ее на основные формы, для которых вы можете легко вычислить площадь.
Хотите изменить единицу площади? Просто нажмите на название устройства, и появится раскрывающийся список.
Формула площади
Вы забыли, что такое формула площади? Тогда вы попали в нужное место. Площадь квадрата равна длине его сторон:
-
Площадь квадрата = a * a = a² , где a — сторона квадрата
Это самая основная и наиболее часто используемая формула, хотя существуют и другие.Например, есть формулы площади, в которых используются диагональ, периметр, радиус описанной окружности или внутренний радиус.
Формула площади прямоугольника
Формула площади прямоугольника тоже несложная задача — это просто умножение сторон прямоугольника:
Расчет площади прямоугольника чрезвычайно полезен в повседневных ситуациях: от строительства здания (оценка необходимой плитки, настила, сайдинга или определение площади крыши) до декорирования вашей квартиры (сколько краски или обоев мне нужно?) До расчета количества людей ваш листовой торт может накормить.
Формула площади треугольника
Существует множество различных формул для вычисления площади треугольника, в зависимости от того, что дано и какие законы или теоремы используются. В этом калькуляторе площади мы реализовали четыре из них:
1. Данные база и высота
-
Площадь треугольника = b * h / 2
2. Даны две стороны и угол между ними (SAS)
-
Площадь треугольника = 0.5 * а * б * sin (γ)
3. Даны три стороны (SSS) (Эта формула площади треугольника называется формулой Герона )
-
Площадь треугольника = 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))
4. Даны два угла и сторона между ними (ASA)
-
Площадь треугольника = a² * sin (β) * sin (γ) / (2 * sin (β + γ))
Есть треугольник особого вида, прямоугольный. В этом случае основание и высота — это две стороны, которые образуют прямой угол. Тогда площадь прямоугольного треугольника может быть выражена как:
В этом случае основание и высота — это две стороны, которые образуют прямой угол. Тогда площадь прямоугольного треугольника может быть выражена как:
Площадь прямоугольного треугольника = a * b / 2
Формула площади круга
Формула площади круга — одна из самых известных формул:
-
Площадь круга = πr² , где r — радиус окружности
В этом калькуляторе мы реализовали только это уравнение, но в нашем круговом калькуляторе вы можете рассчитать площадь по двум разным формулам:
- Диаметр
-
Площадь круга = πr² = π * (d / 2) ²
- Окружность
Кроме того, формула площади круга удобна в повседневной жизни — как серьезная дилемма, какой размер пиццы выбрать.
Формула площади сектора
Формулу площади сектора можно найти, взяв пропорцию круга. Площадь сектора пропорциональна его углу, поэтому, зная формулу площади круга, мы можем записать, что:
α / 360 ° = Площадь сектора / Площадь круга
Преобразование угла говорит нам, что 360 ° = 2π
α / 2π = Площадь сектора / πr²
так:
-
Площадь сектора = r² * α / 2
Формула площади эллипса
Чтобы найти формулу площади эллипса, сначала вспомните формулу площади круга: πr² . Для эллипса у вас есть не одно значение радиуса, а два разных значения:
Для эллипса у вас есть не одно значение радиуса, а два разных значения: a и b . Единственная разница между формулой площади круга и эллипса заключается в замене r² произведением большой и малой полуосей, a * b :
-
Площадь эллипса = π * a * b
Формула площади трапеции
Площадь трапеции можно найти по следующей формуле:
-
Площадь трапеции = (a + b) * h / 2 , где a и b — длины параллельных сторон, а h — высота
Также формула площади трапеции может быть выражена как:
Площадь трапеции = м * ч , где м — среднее арифметическое длин двух параллельных сторон
Площадь формулы параллелограмма
Если вы хотите рассчитать площадь с учетом основания и высоты, сторон и угла или диагоналей параллелограмма и угла между ними, вы находитесь в правильном месте. В нашем инструменте вы найдете три формулы площади параллелограмма:
В нашем инструменте вы найдете три формулы площади параллелограмма:
1. Основание и высота
-
Площадь параллелограмма = a * h
2. Стороны и угол между ними
-
Площадь параллелограмма = a * b * sin (α)
3. Диагонали и угол между ними
-
Площадь параллелограмма = e * f * sin (θ)
Площадь формулы ромба
Мы реализовали три полезные формулы для вычисления площади ромба.Вы можете найти этот район, если знаете:
1. Сторона и высота
2. Диагонали
-
Площадь ромба = (e * f) / 2
3. Сторона и любой угол, например, α
-
Площадь ромба = a² * sin (α)
Площадь формулы воздушного змея
Для расчета площади воздушного змея можно использовать два уравнения, в зависимости от того, что известно:
- Площадь формулы воздушного змея с учетом диагоналей змея
- Площадь формулы воздушного змея с учетом двух несовпадающих длин сторон и угла между этими двумя сторонами
-
Площадь змеевика = a * b * sin (α)
Формула площади пятиугольника
Площадь пятиугольника можно рассчитать по формуле:
-
Площадь пятиугольника = a² * √ (25 + 10√5) / 4 , где a — сторона правильного пятиугольника
Ознакомьтесь с нашим специальным инструментом пятиугольник, в котором представлены другие важные свойства правильного пятиугольника: сторона, диагональ, высота и периметр, а также радиус описанной и вписанной окружности.
Площадь шестиугольника формулы
Основная формула площади шестиугольника:
-
Площадь шестиугольника = 3/2 * √3 * a² , где a — сторона правильного шестиугольника
Так откуда взялась формула? Вы можете представить себе правильный шестиугольник как набор шести равносторонних треугольников. Чтобы найти площадь шестиугольника, все, что нам нужно сделать, это найти площадь одного треугольника и умножить ее на шесть. Формула для площади правильного треугольника равна квадрату стороны, умноженному на квадратный корень из 3, деленный на 4:
.
Площадь равностороннего треугольника = (a² * √3) / 4
Площадь шестиугольника = 6 * Площадь равностороннего треугольника = 6 * (a² * √3) / 4 = 3/2 * √3 * a²
Площадь восьмиугольника по формуле
Чтобы найти площадь восьмиугольника, все, что вам нужно сделать, это знать длину стороны и формулу ниже:
-
Площадь восьмиугольника = 2 * (1 + √2) * a²
Площадь восьмиугольника также можно рассчитать по:
Площадь восьмиугольника = периметр * апофема / 2
Периметр в восьмиугольном корпусе просто 8 * . А что такое апофема? Апофема — это расстояние от центра многоугольника до середины стороны. В то же время это высота треугольника, образованного линией от вершин восьмиугольника к его центру. Этот треугольник — один из восьми совпадающих — является равнобедренным треугольником, поэтому его высоту можно рассчитать, например, с помощью теоремы Пифагора по формуле:
А что такое апофема? Апофема — это расстояние от центра многоугольника до середины стороны. В то же время это высота треугольника, образованного линией от вершин восьмиугольника к его центру. Этот треугольник — один из восьми совпадающих — является равнобедренным треугольником, поэтому его высоту можно рассчитать, например, с помощью теоремы Пифагора по формуле:
h = (1 + √2) * a / 4
Итак, наконец, мы получаем первое уравнение:
Площадь восьмиугольника = периметр * апофема / 2 = (8 * a * (1 + √2) * a / 4) / 2 = 2 * (1 + √2) * a²
Формула площади кольцевого пространства
Кольцо — это объект в форме кольца — это область, ограниченная двумя концентрическими окружностями разного радиуса.Найти формулу площади кольца — простая задача, если вы помните формулу площади круга. Вы только посмотрите: площадь кольца — это разница площадей большего круга радиуса R и меньшего радиуса r:
-
Площадь кольца = πR² - πr² = π (R² - r²)
Кстати, вы видели наш конвертер размера кольца?
Площадь четырехугольника
Четырехугольная формула, которую реализует этот калькулятор площади, использует две заданные диагонали и угол между ними.
-
Площадь четырехугольника = e * f * sin (α) , где e, f — диагонали
Мы можем использовать любой из двух углов, так как мы вычисляем их синус. Зная, что два соседних угла являются дополнительными, мы можем утверждать, что sin (угол) = sin (180 ° - угол) .
Если вы ищете другие формулы для определения площади четырехугольника, воспользуйтесь нашим специальным инструментом для четырехугольника, где вы найдете формулу Бретшнайдера (с учетом четырех сторон и двух противоположных углов) и формулу, в которой используются бимедианы и угол между ними .
Формула площади правильного многоугольника
Формула для площади правильного многоугольника выглядит следующим образом:
-
Площадь правильного многоугольника = n * a² * детская кроватка (π / n) / 4
где n — количество сторон, а a — длина стороны.
Существуют и другие уравнения, в которых используются, например, такие параметры, как радиус описанной окружности или периметр. Вы можете найти эти формулы в специальном абзаце нашего калькулятора площади многоугольника.
Вы можете найти эти формулы в специальном абзаце нашего калькулятора площади многоугольника.
Если вы имеете дело с неправильным многоугольником, помните, что вы всегда можете разделить фигуру на более простые фигуры.Просто посчитайте площадь каждого из них и в конце просуммируйте их. Разбиение многоугольника на набор треугольников называется триангуляцией многоугольника.
Что такое область 2D-форм?
Что такое площадь 2D-фигур?
Площадь любой 2D-формы — это размер области, заключенной в нее. Есть несколько 2D-форм, таких как квадрат, прямоугольник, круг, ромб и треугольник. Цветная область в каждой форме представляет область соответствующей формы.
Единица площади называется квадратными.У разных форм есть разные формулы для расчета площади.
Площадь квадрата и прямоугольника :
Площадь квадрата и прямоугольника равна произведению двух смежных сторон.
2D Форма
Формула площади
Пример
Квадрат
Площадь квадрата = Сторона × Сторона
Площадь = S × S
Площадь = 4 × 4 = 16 кв.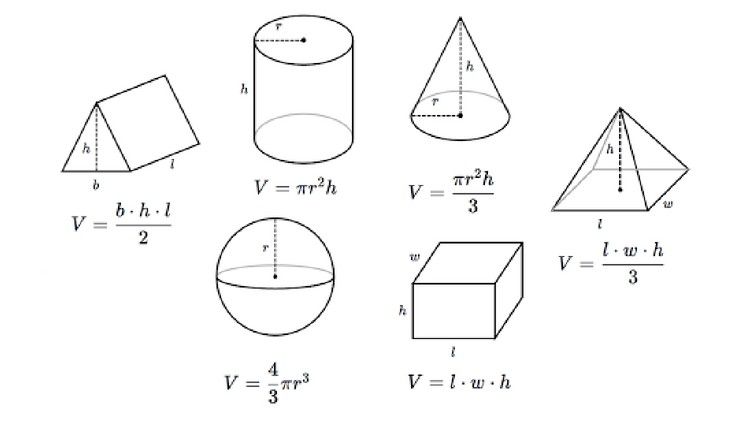 размеры в см
размеры в см
Прямоугольник
Площадь прямоугольника = длина × ширина
= длина × ширина
Площадь = 8 × 3 = 24 кв. См
Площадь треугольника :
Треугольники могут быть разных типов, например равносторонний треугольник, равнобедренный треугольник и прямоугольный треугольник, но формула для площади всех видов треугольников одинакова.
Площадь треугольника определяется по формуле: 1 ⁄ 2 × b × h, где основание (b) — длина любой стороны треугольника, а высота (h) — расстояние по перпендикуляру между основанием. и верхняя вершина треугольника.
Пример:
В треугольнике ABC основание составляет 6 единиц, а высота — 4 единицы.
Итак, площадь треугольника ABC = 1 ⁄ 2 × b × h
= 1 ⁄ 2 × 6 × 4
= 12 кв. Единиц
Круг :
Площадь круга вычисляется по формуле π × r 2 , где r — радиус круга, а π — постоянная величина, значение которой равно 227 или 3.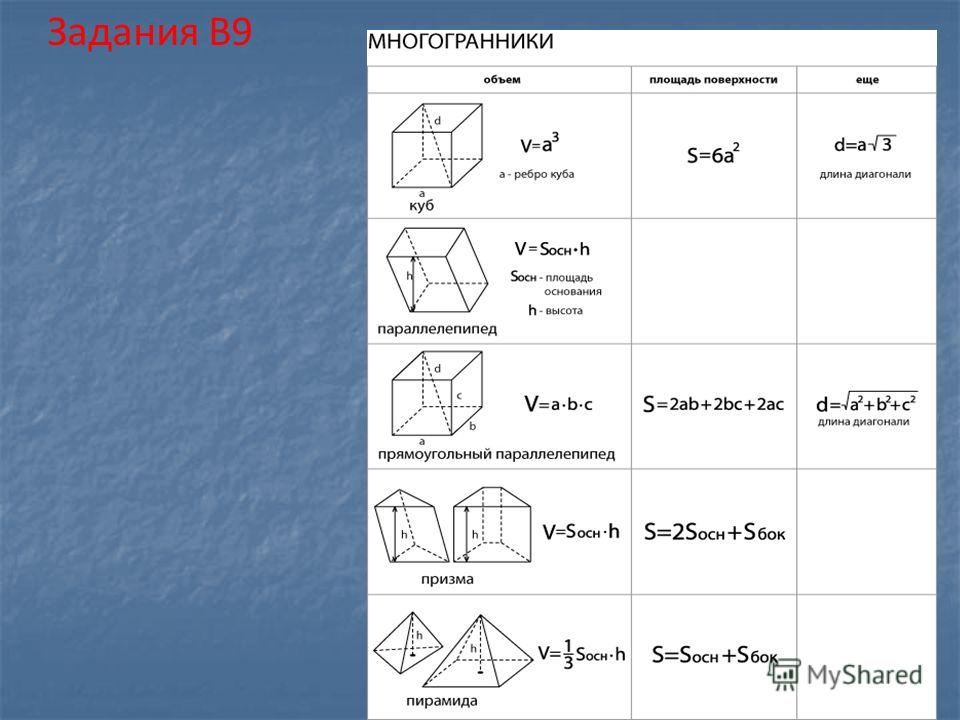 14
14
Пример: Площадь вышеуказанного круга = π × r 2
= 3,14 × 4 2
= 3,14 × 16
= 50,24 кв. См
Ромб :
Формула для определения площади ромба: pq / 2, где p и q — две диагонали ромба.
В ромбе ABCD площадь можно вычислить следующим образом:
Площадь ромба = 1 ⁄ 2 pq
= 1 ⁄ 2 × 3 × 5
= 7,5 см кв.
Параллелограмм :
Чтобы найти площадь параллелограмма, мы используем формулу b × h, где b обозначает основание, а h обозначает высоту. Высота — это расстояние по вертикали между основанием и верхом.
Пример:
На приведенном выше рисунке площадь параллелограмма равна b × h. Следовательно, это 6 × 4 = 24 кв. См
Расчетная область | SkillsYouNeed
Площадь — это мера того, сколько места внутри фигуры. Расчет площади формы или поверхности может быть полезен в повседневной жизни — например, вам может потребоваться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы засеять лужайку.
Расчет площади формы или поверхности может быть полезен в повседневной жизни — например, вам может потребоваться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы засеять лужайку.
На этой странице описаны основные сведения, которые вам необходимо знать, чтобы понять и вычислить площади общих форм, включая квадраты и прямоугольники, треугольники и круги.
Расчет площади по сетке
Когда фигура рисуется на масштабированной сетке, вы можете найти площадь, подсчитав количество квадратов сетки внутри фигуры.
В этом примере внутри прямоугольника 10 квадратов сетки.
Чтобы найти значение площади с использованием метода сетки, нам нужно знать размер, который представляет квадрат сетки.
В этом примере используются сантиметры, но тот же метод применяется к любой единице длины или расстояния. Например, вы можете использовать дюймы, метры, мили, футы и т. Д.
В этом примере каждый квадрат сетки имеет ширину 1 см и высоту 1 см. Другими словами, каждый квадрат сетки равен одному квадратному сантиметру.
Другими словами, каждый квадрат сетки равен одному квадратному сантиметру.
Подсчитайте квадраты сетки внутри большого квадрата, чтобы найти его площадь.
Есть 16 маленьких квадратов, поэтому площадь большого квадрата составляет 16 квадратных сантиметров.
В математике мы сокращаем «квадратные сантиметры» до 2 . 2 означает «квадрат».
Каждый квадрат сетки равен 1 см 2 .
Площадь большого квадрата 16см 2 .
Подсчет квадратов на сетке для определения площади работает для всех форм — если известны размеры сетки. Однако этот метод становится более сложным, когда фигуры не точно соответствуют сетке или когда вам нужно подсчитать доли квадратов сетки.
В этом примере квадрат не точно помещается на сетке.
Мы все еще можем вычислить площадь, считая квадраты сетки.
- Имеется 25 квадратов полной сетки (заштрихованы синим цветом).
- 10 квадратов полусетки (заштрихованы желтым цветом) — 10 полуквадратов равны 5 полным квадратам.
- Также есть 1 четверть квадрата (заштрихована зеленым) — (или 0,25 целого квадрата).
- Сложите целые квадраты и дроби вместе: 25 + 5 + 0.25 = 30,25.
Следовательно, площадь этого квадрата составляет 30,25 см 2 .
Вы также можете записать это как 30¼см 2 .
Хотя использование сетки и подсчета квадратов внутри фигуры является очень простым способом изучения концепций площади, оно менее полезно для нахождения точных областей с более сложными формами, когда можно сложить много частей квадратов сетки.
Площадь можно рассчитать с помощью простых формул, в зависимости от типа фигуры, с которой вы работаете.
Остальная часть этой страницы объясняет и дает примеры того, как вычислить площадь фигуры без использования системы сеток.
Площади простых четырехугольников:
квадратов, прямоугольников и параллелограммов
Простейшие (и наиболее часто используемые) вычисления площади выполняются для квадратов и прямоугольников.
Чтобы найти площадь прямоугольника, умножьте его высоту на ширину.
Для квадрата вам нужно только найти длину одной из сторон (поскольку каждая сторона имеет одинаковую длину), а затем умножить это на себя, чтобы найти площадь.Это то же самое, что сказать длину 2 или длину в квадрате.
Рекомендуется проверять, является ли фигура квадратом, измеряя две стороны. Например, стена комнаты может выглядеть как квадрат, но когда вы ее измеряете, вы обнаруживаете, что на самом деле это прямоугольник.
Часто в реальной жизни формы могут быть более сложными. Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.
Типовой план помещения не может состоять из простого прямоугольника или квадрата:
В этом и других подобных примерах фокус состоит в том, чтобы разделить фигуру на несколько прямоугольников (или квадратов).Неважно, как вы разделите фигуру — любое из трех решений даст один и тот же ответ.
Для решений 1 и 2 необходимо создать две фигуры и сложить их площади, чтобы найти общую площадь.
Для решения 3 вы создаете большую форму (A) и вычитаете из нее меньшую форму (B), чтобы найти площадь.
Другая распространенная проблема — найти область границы — фигуры внутри другой фигуры.
В этом примере показана дорожка вокруг поля — ширина дорожки 2 метра.
Опять же, в этом примере есть несколько способов определить площадь пути.
Вы можете просмотреть путь как четыре отдельных прямоугольника, вычислить их размеры, а затем их площадь и, наконец, сложить области, чтобы получить итог.
Более быстрый способ — вычислить площадь всей формы и площадь внутреннего прямоугольника. Вычтите площадь внутреннего прямоугольника из всей, оставив площадь пути.
- Площадь всей формы составляет 16 м × 10 м = 160 м 2 .
- Мы можем определить размеры средней секции, потому что знаем, что дорожка по краю имеет ширину 2 метра.

- Ширина всей формы составляет 16 м, а ширина пути по всей форме — 4 м (2 м слева от формы и 2 м справа). 16 м — 4 м = 12 м
- То же самое для высоты: 10м — 2м — 2м = 6м
- Итак, мы подсчитали, что средний прямоугольник имеет размер 12 × 6 м.
- Таким образом, площадь среднего прямоугольника составляет: 12 м × 6 м = 72 м 2 .
- Наконец, мы убираем область среднего прямоугольника из области всей формы. 160 — 72 = 88м 2 .
Площадь тропы 88м 2 .
Параллелограмм — это четырехгранная форма с двумя парами сторон равной длины — по определению прямоугольник является разновидностью параллелограмма. Однако большинство людей склонны думать о параллелограммах как о четырехсторонних фигурах с наклонными линиями, как показано здесь.
Площадь параллелограмма рассчитывается так же, как и для прямоугольника (высота × ширина), но важно понимать, что высота означает не длину вертикальных (или отклоненных от вертикали) сторон, а расстояние между сторонами.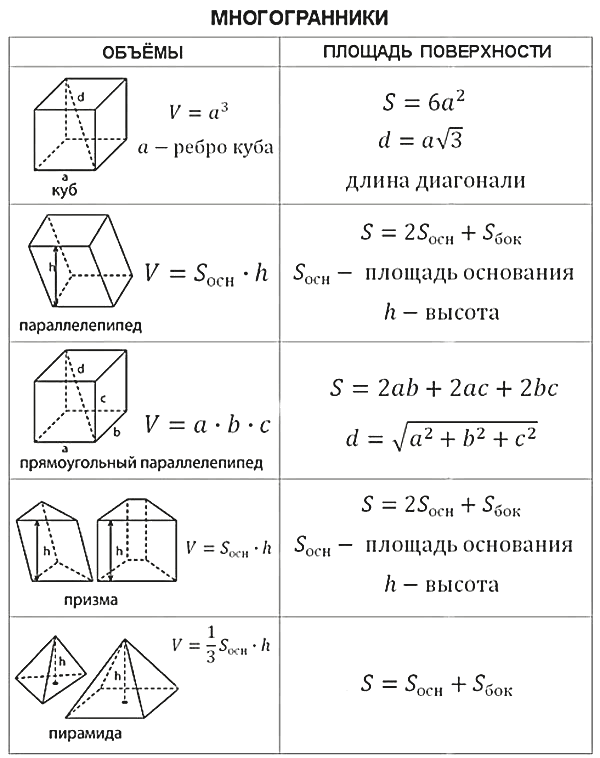
Из диаграммы вы можете видеть, что высота — это расстояние между верхней и нижней сторонами фигуры, а не длина стороны.
Представьте себе воображаемую линию под прямым углом между верхней и нижней сторонами. Это высота.
Области треугольников
Может быть полезно думать о треугольнике как о половине квадрата или параллелограмма.
Предполагая, что вы знаете (или можете измерить) размеры треугольника, вы можете быстро вычислить его площадь.
Площадь треугольника (высота × ширина) ÷ 2.
Другими словами, вы можете вычислить площадь треугольника так же, как площадь квадрата или параллелограмма, а затем просто разделите свой ответ на 2.
Высота треугольника измеряется по прямой линии от нижней линии (основания) до «вершины» (верхней точки) треугольника.
Вот несколько примеров:
Площадь трех треугольников на диаграмме выше одинакова.
Каждый треугольник имеет ширину и высоту 3 см.
Площадь рассчитана:
(высота × ширина) ÷ 2
3 × 3 = 9
9 ÷ 2 = 4,5
Площадь каждого треугольника составляет 4,5 см 2 .
В реальных ситуациях вы можете столкнуться с проблемой, требующей найти площадь треугольника, например:
Вы хотите покрасить фронтальный конец сарая. Вам нужно посетить магазин украшений только один раз, чтобы получить нужное количество краски.Вы знаете, что литр краски покроет 10 м 2 стены. Сколько краски нужно, чтобы покрыть фронтон?
Вам нужно три измерения:
A — Общая высота до вершины крыши.
B — Высота вертикальных стен.
C — Ширина здания.
В этом примере измерения:
A — 12,4 м
B — 6,6 м
C — 11,6 м
Следующий этап требует дополнительных расчетов.Подумайте о здании как о двух формах: прямоугольнике и треугольнике. По имеющимся у вас измерениям вы можете рассчитать дополнительное измерение, необходимое для определения площади фронтона.
Размер D = 12,4 — 6,6
D = 5,8 м
Теперь вы можете определить площадь двух частей стены:
Площадь прямоугольной части стены: 6,6 × 11,6 = 76,56 м 2
Площадь треугольной части стены: (5.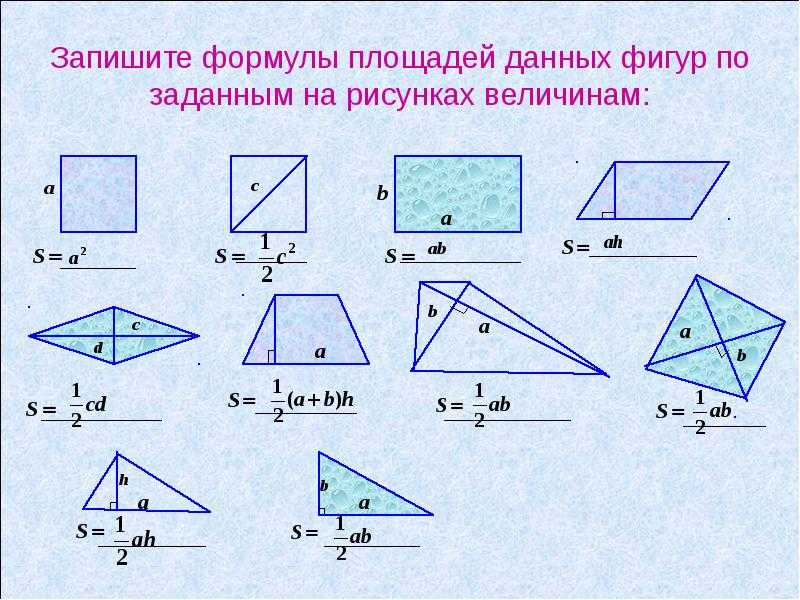 8 × 11,6) ÷ 2 = 33,64 м 2
8 × 11,6) ÷ 2 = 33,64 м 2
Сложите эти две области вместе, чтобы получить общую площадь:
76,56 + 33,64 = 110,2 м 2
Как вы знаете, один литр краски покрывает 10 м 2 стены, поэтому мы можем рассчитать, сколько литров нам нужно купить:
110,2 ÷ 10 = 11,02 л.
На самом деле вы можете обнаружить, что краска продается только в 5-литровых или 1-литровых канистрах, результат — чуть более 11 литров. У вас может возникнуть соблазн округлить до 11 литров, но, если мы не будем разбавлять краску водой, этого будет недостаточно.Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски. Это позволит избежать потерь и оставит большую часть литра для подкраски позднее. И не забывайте, что если вам нужно нанести более одного слоя краски, вы должны умножить количество краски для одного слоя на количество необходимых слоев!
Области кругов
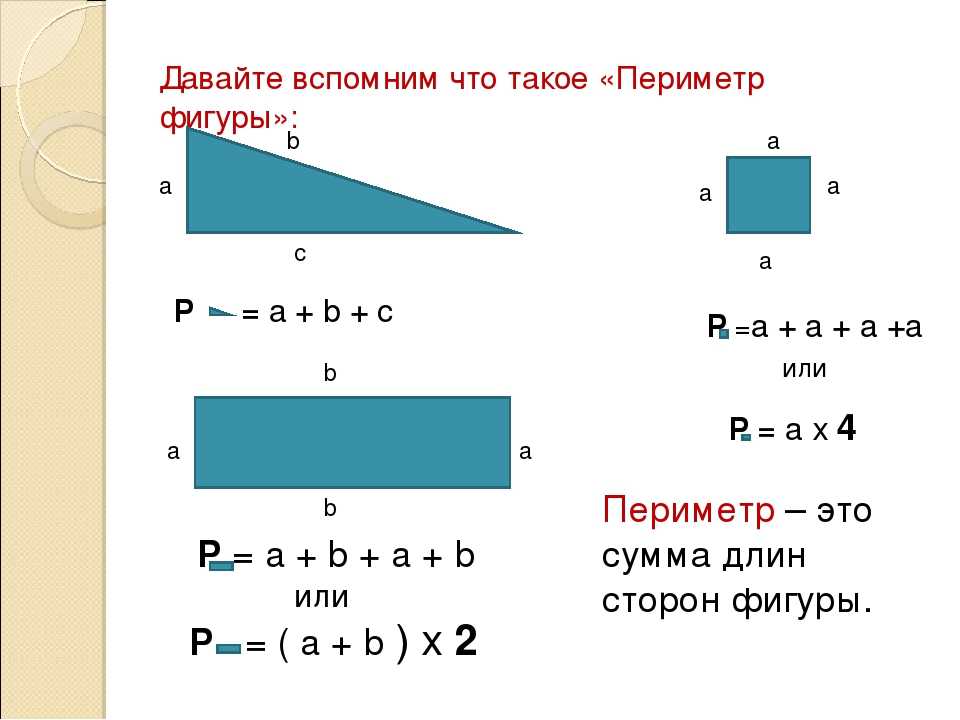
Чтобы вычислить площадь круга, вам необходимо знать его диаметр или радиус .
Диаметр круга — это длина прямой линии от одной стороны круга до другой, проходящей через центральную точку круга. Диаметр в два раза больше длины радиуса (диаметр = радиус × 2)
Радиус круга — это длина прямой линии от центральной точки круга до его края. Радиус составляет половину диаметра. (радиус = диаметр ÷ 2)
Вы можете измерить диаметр или радиус в любой точке окружности — важно измерять, используя прямую линию, проходящую через (диаметр) или заканчивающуюся в (радиусе) центром окружности.
На практике при измерении окружностей часто легче измерить диаметр, а затем разделить на 2, чтобы найти радиус.
Радиус нужен для вычисления площади круга, формула:
площадь круга = πR 2 .
Это означает:
π = Pi — постоянная, равная 3,142.
R = радиус окружности.
R 2 (радиус в квадрате) означает радиус × радиус.
Следовательно, круг с радиусом 5 см имеет площадь:
3. 142 × 5 × 5 = 78,55 см 2 .
142 × 5 × 5 = 78,55 см 2 .
Круг диаметром 3 м имеет площадь:
Сначала прорабатываем радиус (3м ÷ 2 = 1,5м)
Затем примените формулу:
πR 2
3,142 × 1,5 × 1,5 = 7,0695.
Площадь круга диаметром 3 м составляет 7,0695 м 2 .
Последний пример
В этом примере используется большая часть содержимого этой страницы для решения простых задач с областями.
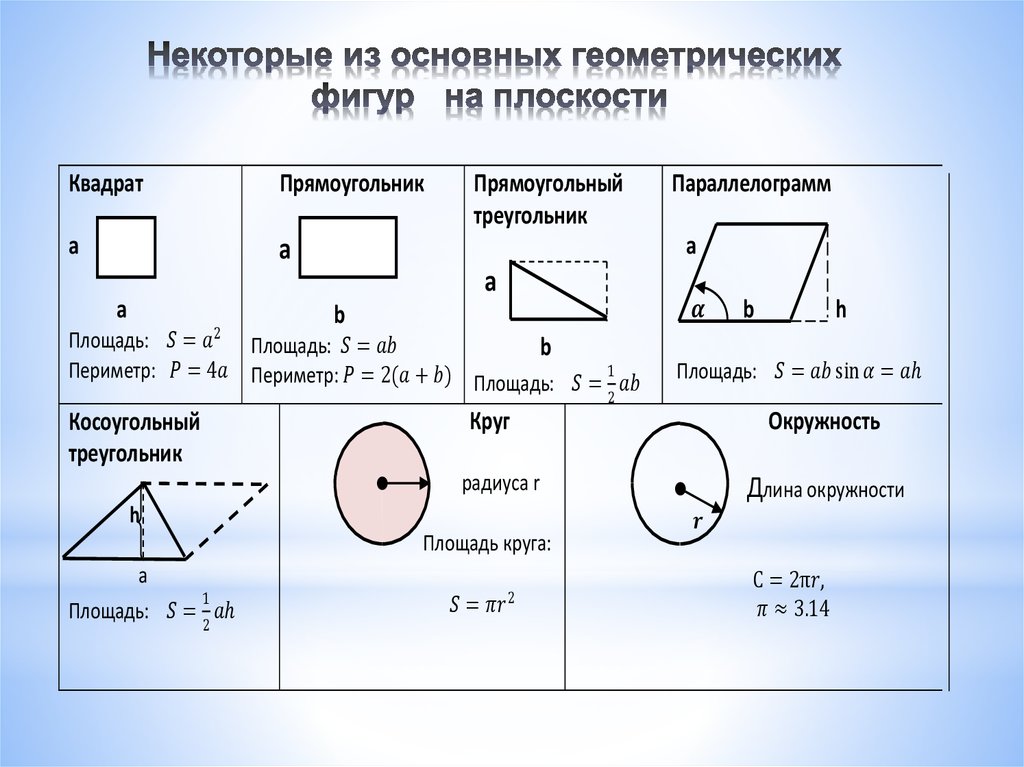
Это дом Рубена М. Бенджамина в Блумингтоне, штат Иллинойс, внесенный в Национальный реестр исторических мест США (номер записи: 376599).
Этот пример включает поиск передней части дома, деревянной решетчатой части — исключая дверь и окна. Вам нужны следующие размеры:
A — 9,7 м
B — 7,6 м
C — 8,8 м
D — 4,5 м
Е — 2.3 мес.
F — 2,7 м
G — 1,2 м
H — 1,0 м
Примечания:
- Все размеры являются приблизительными.
- Не нужно беспокоиться о бордюре вокруг дома — она не учтена в измерениях.
- Мы предполагаем, что все прямоугольные окна имеют одинаковый размер.
- Размер круглого окна — это диаметр окна.
- Размер двери включает ступеньки.
Какова площадь деревянной реечной части дома?
Работы и ответы ниже:
Ответы на приведенный выше пример
Сначала определите площадь основной формы дома — прямоугольника и треугольника, составляющих форму.
Главный прямоугольник (B × C) 7,6 × 8,8 = 66,88 м 2 .
Высота треугольника (A — B) 9,7 — 7,6 = 2,1.
Следовательно, площадь треугольника равна (2.1 × C) ÷ 2.
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м 2 .
Общая площадь фасада дома равна сумме площадей прямоугольника и треугольника:
66,88 + 9,24 = 76,12 м 2 .
Затем проработайте площади окон и дверей, чтобы их можно было вычесть из всей площади.
Площадь двери и ступенек составляет (Д × В) 4,5 × 2,3 = 10,35 м 2 .
Площадь одного прямоугольного окна составляет (G × F) 1.2 × 2,7 = 3,24 м 2 .
Есть пять прямоугольных окон. Умножьте площадь одного окна на 5.
3,24 × 5 = 16,2 м2. (общая площадь прямоугольных окон).
Круглое окно имеет диаметр 1 м, поэтому радиус 0,5 м.
Используя πR 2 , определите площадь круглого окна: 3,142 × 0,5 × 0,5 =. 0,7855м 2 .
Затем сложите площади двери и окон.
(зона двери) 10,35 + (прямоугольная зона окон) 16.2 + (площадь круглого окна) 0,7855 = 27,3355
Наконец, вычтите общую площадь окон и дверей из всей площади.
76,12 — 27,3355 = 48,7845
Площадь деревянного реечного фасада дома, и ответ на проблему: 48,7845м 2 .
Вы можете округлить ответ до 48,8 м 2 или 49 м 2 .
См. Нашу страницу Оценка, приближение и округление .
Площадь фигур | Сеточная техника | Формулы
Содержание
14 декабря 2020
Время чтения: 5 минут
Введение
Наш мир полон удивительных форм.
Круги и овалы
Квадрат и прямоугольники,
Звезды и треугольники.
Интересно узнать о различных формах и их структуре.
Вы используете множество предметов разной формы в повседневной жизни и на работе.
В этой статье вы узнаете о различных типах фигур и о том, как рассчитать площадь фигур.
Геометрия — это наука, в которой вы изучаете типы форм и их размеры. Он разработал формулы для определения площади определенных форм.
Часто возникает необходимость рассчитать площадь поверхности, покрытую этими объектами. Начнем с определения области.
Как найти области различной формы в геометрии-PDF
Узнайте о различных формах и о том, как рассчитать их площади, о технике сетки и реальных примерах. Вот загружаемый PDF-файл, чтобы узнать больше.
Вот загружаемый PDF-файл, чтобы узнать больше.
📥
Как найти области различной формы в геометрии-PDF
Загрузить
Также читайте,
Что такое «Площадь»?
Слово «Площадь» на латыни означает свободную поверхность.Площадь можно определить как пространство, занимаемое плоской поверхностью определенной формы.
Измеряется в «количестве» квадратных единиц. (квадратные сантиметры, квадратные дюймы, квадратные футы и т. Д.).
Знание формы поверхности помогает нам в повседневной жизни. Это помогает общаться или давать информацию в практической жизни.
Например, площадь участка можно использовать для расчета площади поверхности, доступной для строительства, или площади комнаты, которую можно рассчитать, чтобы определить размер используемого ковра.
У большинства объектов или фигур есть края и углы. Длина и ширина этих краев учитываются для расчета площади конкретной формы.
Как использовать технику сетки, чтобы найти площадь?
Сеточные методы могут помочь нам лучше понять эти формулы.
Нарисуем фигуру на масштабированной сетке. Площадь можно найти, посчитав количество квадратов, покрывающих внутреннюю часть фигуры.
На этом рисунке 6 квадратов сетки в прямоугольнике. Следует знать размеры квадрата сетки.
Может быть в сантиметрах, дюймах или футах. Предположим, что ширина 1 квадрата составляет 1 см, тогда площадь прямоугольника, как на этой картинке, будет 6 квадратных сантиметров. Идея в том, сколько квадратов покрывают внутреннее пространство формы.
Формулы для расчета площадей различной формы
Квадрат
Чтобы вычислить площадь квадрата, нужно просто знать длину одной стороны квадрата и умножить это число на себя.
Напр. если длина квадрата 4 см, то площадь 4 см x 4 см = 16 см 2.
Прямоугольник
Чтобы найти площадь прямоугольника, нужно знать его длину и ширину.
Площадь можно вычислить, просто умножив длину на ширину.
Напр. Длина прямоугольника 4 см, ширина 5 см.
Таким образом, площадь будет: 4 см x 5 см = 20 см².
Треугольник
Посмотрите на картинку ниже. Если вы заметили, треугольник — это половина квадрата или параллелограмма. Естественно, его площадь составляла бы половину квадрата / параллелограмма.
т.е. (длина x высота) / 2
Теперь высоту треугольника можно измерить, проведя прямую (прямоугольную) линию от основания треугольника до вершины (верхнего угла треугольника).
Здесь, в приведенном выше примере, площадь треугольника будет 4 × 3/2 = 6 кв. См.
Круг
Чтобы получить площадь круга, нужно знать его диаметр или радиус.
Радиус круга — это длина линии от центральной точки круга к его краю. Радиус составляет половину диаметра.
Диаметр — это линия, проведенная между двумя краями окружностей, проходящих через центр той же окружности.
Формула для определения площади круга: π × r 2 , где значение π (3.142) постоянно.
Следовательно, площадь круга равна: 3,142 × Радиус круга 2
Напр. Радиус круга 3 см. тогда площадь будет: 3,142 × 3 2 = 28,278 кв. см.
Некоторые примеры из реальной жизни на области фигур
Вы можете применить эти формулы, чтобы получить площади различной формы.
1. Предположим, Джини получил 4 куска одной пиццы среднего размера, а Джони получил 3 куска другой пиццы большого размера. Как Джини и Джони узнают, у кого больше пиццы?
Ответ:
Первый шаг: нам нужно рассчитать площадь обеих пицц. Для этого мы рассмотрим радиус его диаметра, поскольку пицца имеет форму круга.
Предположим, пицца среднего размера имеет радиус 10 см. Его площадь составит
кв.
3,142 × 10 2 по формуле.
т.е. π × R 2
Площадь будет:
314,2 кв. См.
Точно так же пицца большого размера имеет радиус 16 см, площадь будет:
3,142 × 16 2 =
804.352 кв. См.
Теперь, когда у нас есть площадь, давайте посмотрим, сколько долей пиццы у Джини и Джона.
У Джини 4 одинаковых кусочка из 6 пиццы среднего размера, которая имеет площадь 62,84 кв. См.
Итак, доля Джини составляет 314.2/6 × 4 = 209,466 кв. См.
И у Джони есть 3 куска одинакового размера из 6 пиццы среднего размера. Который имеет площадь 100 544 кв. См
Его доля составит 804,352 / 6 × 3 = 402,176 кв. См.
Исходя из вышесказанного, мы можем сказать, что у Джонни есть еще пиццы.
2. Необходимо определить площадь стены, на которой будут проводиться малярные работы.
Ответ:
Первый шаг — вычислить всю площадь стены путем измерения высоты и ширины.
Вычитание площади окна / двери путем измерения высоты и ширины окна / двери.
И можно узнать точное направление работы.
Предположим, что высота составляет 11 квадратных футов, а ширина — 10 квадратных футов.
Площадь стены будет: 11 футов × 10 футов (высота × ширина) = 110 квадратных футов
Из этой области нужно исключить область Окна.
Давайте вычислим площадь окна, учитывая высоту и ширину окна.
То же будет 3 фута в высоту и 4 фута в ширину.
Таким образом, площадь окна будет 3 фута × 4 фута = 12 футов.
Следовательно, общая рабочая площадь будет:
110 квадратных футов — 12 квадратных футов = 98 квадратных футов.
Выше показан пример того, как вычислить формы области, которые полезны в повседневной жизни.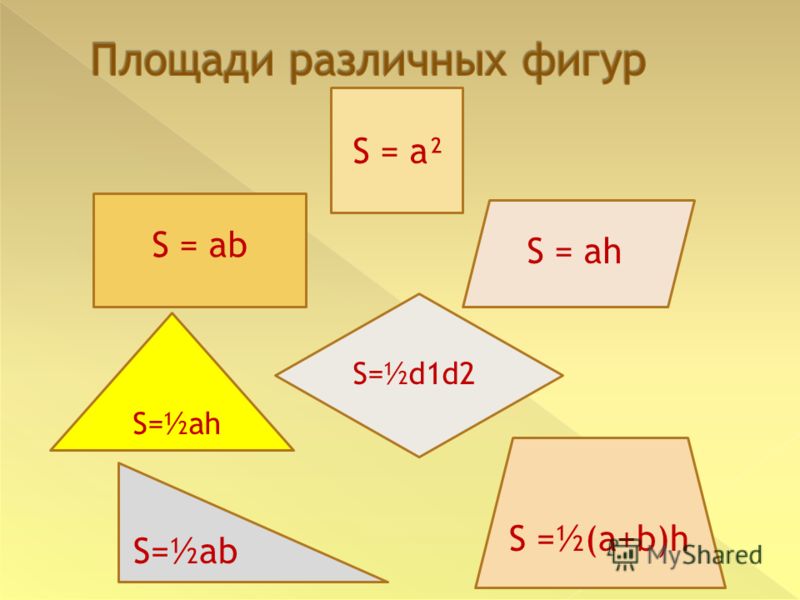
Есть и другие области, в которых нам нужно вычислить площади форм.Формулы помогают получить площади различных и сложных форм.
Что мы узнали
Приведенная ниже таблица содержит некоторые основные формы и формулы для расчета их площадей.
Форма
Чертеж
Формула
Площадь
a² («a» обозначает длину одной стороны квадрата)
Прямоугольник
Длина × Ширина
Треугольник
½ (основание × высота)
Круг
π x R 2 («π» означает — 3.142 & «R» означает — Радиус окружности)
Резюме
Область форм — очень важная тема как для экзаменов, так и для практической жизни, у нее много приложений.
От глиняных табличек вавилонской эры, показывающих расчет площади трапеции до современных формул для различных форм, расчет площади был не только увлекательной областью изучения, но также имел бесконечное практическое применение.
Одинаковые формы с разными областями и разные формы с одинаковыми областями, все они должны быть рассчитаны для различных целей, таких как строительство зданий, покраска областей, укладка плитки, продажа предметов, и список бесконечен.
Для простых форм вы можете использовать технику сетки, чтобы найти область, в противном случае вы можете просто использовать формулы.
Если вы думаете, что эта статья принесет пользу вашим друзьям, не стесняйтесь поделиться ею с ними!
Также читайте,
О компании Cuemath
Cuemath, удобная для учащихся платформа математики и кодирования, проводит регулярные онлайн-классы для преподавателей и развития навыков, а их приложение Mental Math для iOS и Android представляет собой универсальное решение для детей, развивающее несколько навыков.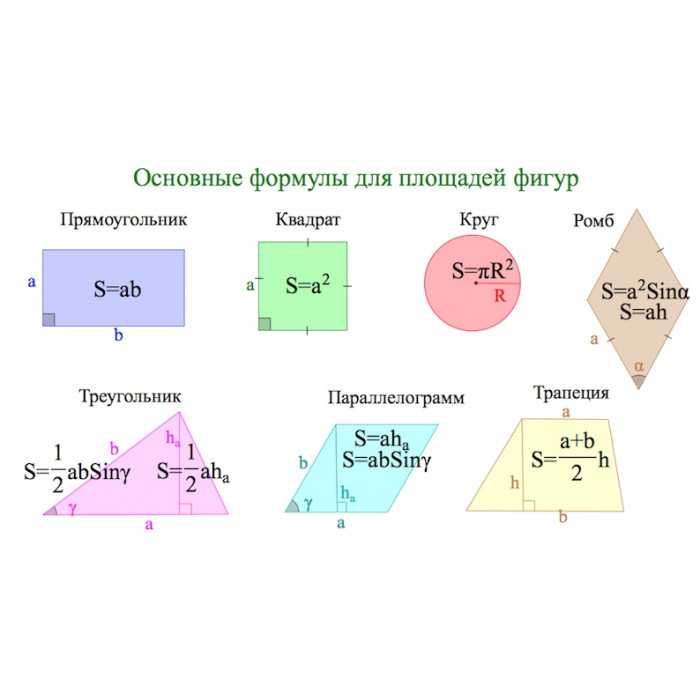
Ознакомьтесь со структурой оплаты для всех классов и закажите пробное занятие сегодня!
Часто задаваемые вопросы
Что такое площадь?
Площадь можно определить как объем пространства, занимаемого плоской поверхностью определенной формы.
Что такое сеточная техника?
Методы сетки
могут помочь нам лучше понять эти формулы для поиска площади. Нарисуйте фигуру на масштабированной сетке. Площадь можно найти, посчитав количество квадратов, покрывающих внутреннюю площадь формы
.
Какие бывают типы фигур?
Различные типы форм:
- Треугольник
- Квадрат
- Прямоугольник
- Пентагон
- Шестиугольник и т. Д.
Какова площадь треугольника?
Если вы заметили, треугольник — это половина квадрата или параллелограмма. Естественно, его площадь будет равна половине квадрата / параллелограмма, т. Е. (Длина x высота) / 2
Е. (Длина x высота) / 2
.
Какова площадь квадрата?
Чтобы вычислить площадь квадрата, нужно просто знать длину одной стороны квадрата и умножить это число на себя.
Что такое площадь прямоугольника?
Чтобы найти площадь прямоугольника, нужно знать его длину и ширину.Просто умножив его длину на ширину, можно вычислить площадь
Что такое площадь круга?
Формула для определения площади круга: π × r 2 , где значение π (3.142) постоянно. Здесь r — радиус круга.
Внешние ссылки
Калькулятор площади
— Расчет площади различной формы
Рассчитайте площадь, выбрав форму и введя свои измерения в любых метрических или обычных единицах США.См. Формулы для расчета площади каждой формы ниже.
Как рассчитать площадь
Площадь — это пространство внутри периметра / границы пространства, его символ — (A). Это размер двухмерной поверхности и измеряется в квадратных единицах, например квадратных футах.
Квадратные футы также могут быть выражены в футах 2 или в квадратных футах. Используйте наши формулы, чтобы найти площадь многих форм.
Перед вычислением площади важно измерить все длины в одной и той же единице измерения или преобразовать все длины в одну и ту же единицу измерения.Воспользуйтесь нашими калькуляторами преобразования единиц длины или калькуляторами преобразования единиц площади для преобразования британских единиц измерения в метрическую.
Используйте приведенные ниже формулы, чтобы вычислить площадь многих популярных фигур.
Формула площади
А = а 2
А = а × а
a = длина кромки
Формула площади прямоугольника
A = длина × ширина
l = длина
w = ширина
Формула приграничной площади
А = (l1 × w1) — (l2 × l2)
l1 = внешняя длина
w1 = внешняя ширина
l2 = внутренняя длина
w2 = внутренняя ширина
Формула площади трапеции
A = 1 / 2 (a + b) h
a = основание a
b = основание b
h = высота
Формула площади параллелограмма
A = b × h
b = основание
h = высота
Формула площади треугольника
s = 1 / 2 (a + b + c)
A = s (s — a) (s — b) (s — c))
a = край a
b = край b
c = край c
Эта формула известна как формула Герона.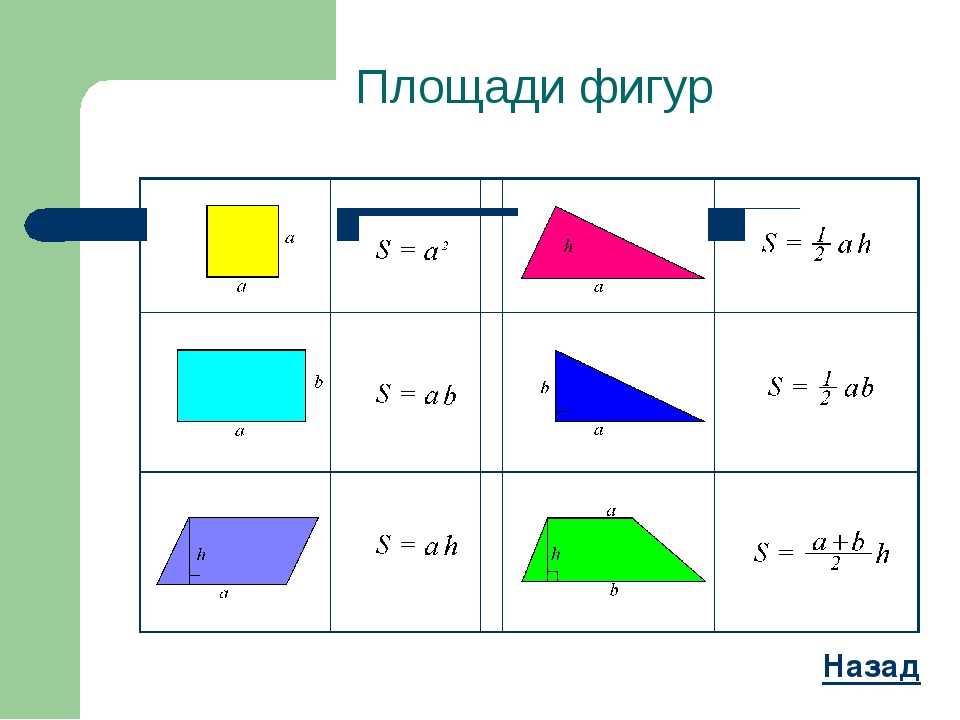 Вы также можете использовать упрощенную формулу, если известна высота треугольника.
Вы также можете использовать упрощенную формулу, если известна высота треугольника.
A = 1 / 2 bh
b = край b
h = высота
Формула площади круга
А = πr 2
r = радиус
Если вам известен диаметр окружности, вы можете найти радиус, разделив диаметр пополам.
Знаете ли вы, что у нас также есть калькулятор для определения площади круга?
Формула площади эллипса
А = πab
a = ось a
b = ось b
Формула площади сектора
А = (θ ÷ 360) πr 2
r = радиус
θ = угол
Узнайте больше о секторах и посмотрите более подробные примеры в нашем калькуляторе площади секторов.
Формула площади правильного многоугольника
A = (a 2 × n) ÷ (4 × tan (π ÷ n))
a = длина кромки
n = количество сторон
Неправильные многоугольники и сложные формы
Уловка для определения площади неправильного многоугольника или сложной формы состоит в том, чтобы сначала разбить форму на правильные многоугольники, такие как треугольники и квадраты, затем найти площадь этих фигур и сложить их вместе, чтобы найти общую сумму.
Разница между площадью и площадью
Вам может быть интересно, чем площадь отличается от площади поверхности.В то время как площадь — это размер двумерной плоскости, площадь поверхности — это размер поверхности трехмерной твердой формы.
Разница между площадью и периметром
Так в чем же разница между периметром и площадью? Периметр — это расстояние вокруг двухмерной фигуры, а площадь — это размер самой фигуры.
Конечно, у нас есть калькулятор периметра, который поможет решить эту проблему с измерением длины.
Иллюстративная математика
Задача
Ниже приведены изображения равностороннего треугольника, квадрата, правильного шестиугольника и круга, каждый из которых имеет
тот же периметр:
-
Найдите площадь равностороннего треугольника, периметр которого равен 1 доллару.
-
Найдите площадь квадрата, периметр которого равен 1 доллару.
-
Найдите площадь правильного шестиугольника, периметр которого равен одной единице.
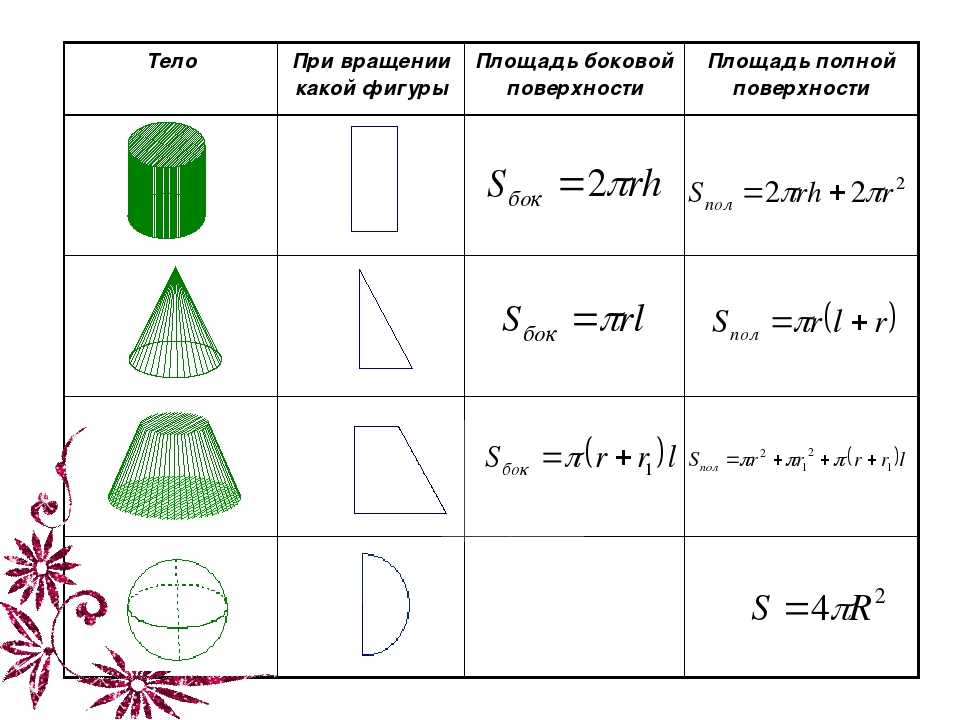
-
Найдите площадь круга, периметр которого равен 1 доллару.
-
Перечислите ответы на (a), (b), (c) и (d) в увеличивающемся размере. Как, по вашему мнению, площадь правильного восьмиугольника с периметром в 1 доллар будет сравниваться с площадью?
треугольник, квадрат, шестиугольник и круг?
Комментарий IM
Эта проблема является частью очень богатой традиции задач, стремящихся максимизировать
площадь, ограниченная фигурой с фиксированным периметром.Здесь рассматриваются только три формы, потому что проблема сложна для более неправильных форм. Для
Например, из всех треугольников тот, у которого фиксированный периметр $ P $ и наибольшая площадь
равносторонний треугольник, все стороны которого равны $ frac {P} {3} $, но это
трудно показать, потому что нелегко найти площадь треугольника в терминах
длины трех сторон (хотя формула Герона позволяет это сделать). Ни
легко ли сравнить площадь двух треугольников с одинаковым периметром без
зная свои индивидуальные области.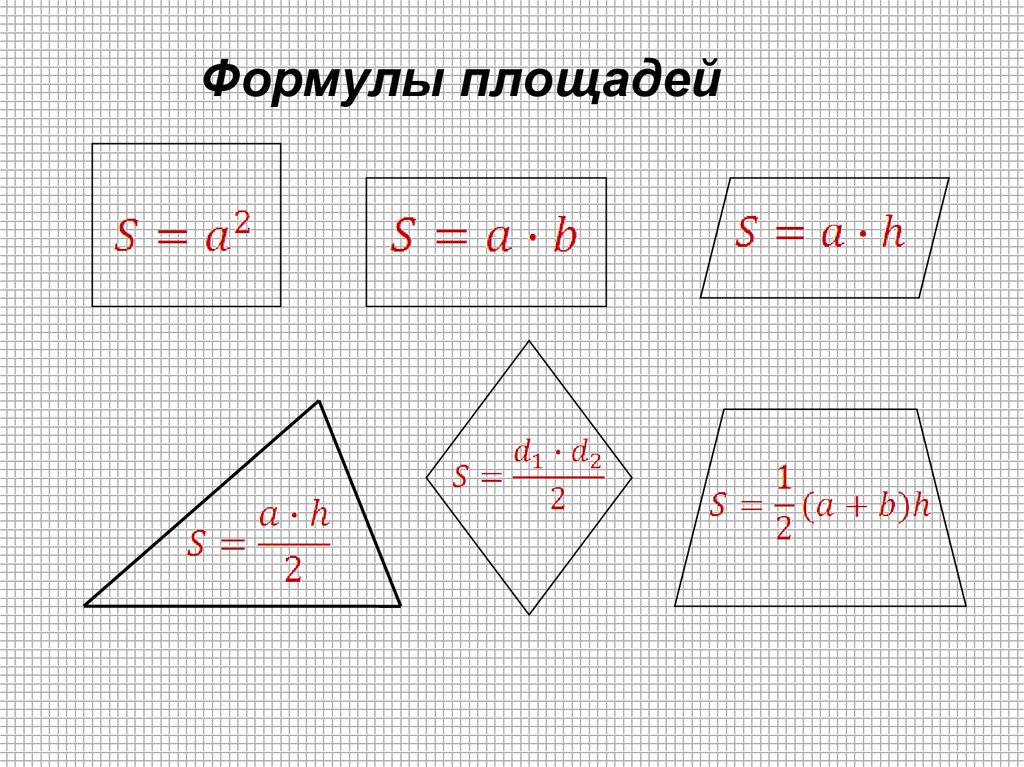 Для четырехугольников возникает аналогичная проблема:
Для четырехугольников возникает аналогичная проблема:
показывая, что из всех прямоугольников с периметром $ P $ тот, у которого наибольший
Площадь — квадрат, длина сторон которого равна $ frac {P} {4} $ — хорошая задача, над которой должны подумать учащиеся. Но сравнить квадрат с четырехугольником неправильной формы равного периметра будет сложно.
Для этой проблемы были выбраны очень явные формы с целью обеспечения
возможность для студентов попрактиковаться, используя свои знания различных
геометрические формулы для площади и периметра.Учитель, чтобы подкрепить
часть (d), возможно, пожелает нарисовать примеры шестиугольника и восьмиугольника (оба разделяют
тот же периметр, что и у других фигур). Основная идея заключается в том, что по мере увеличения количества сторон многоугольника многоугольник становится все больше и больше похож на круг, и, в частности, его площадь приближается к площади круга.
17.07.2020Leave a Comment on Площади разных фигур: Площади геометрических фигур / math5school. ruРазное
ruРазное
Площадь разных фигур. Как вычислить и обозначить площадь. Помещение прямоугольной или квадратной формы
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.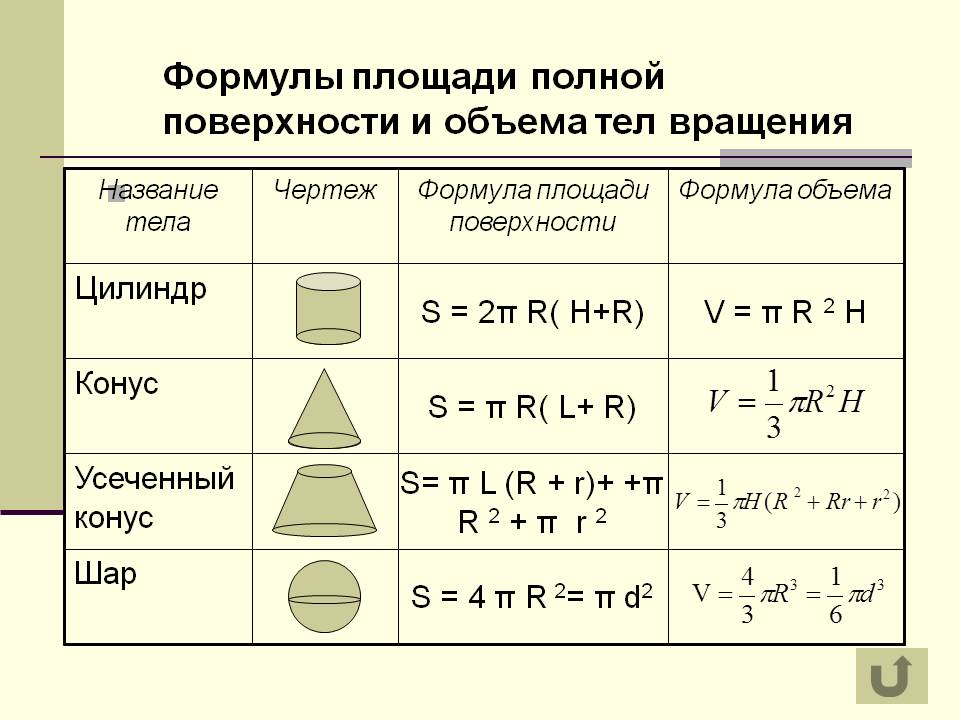
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности.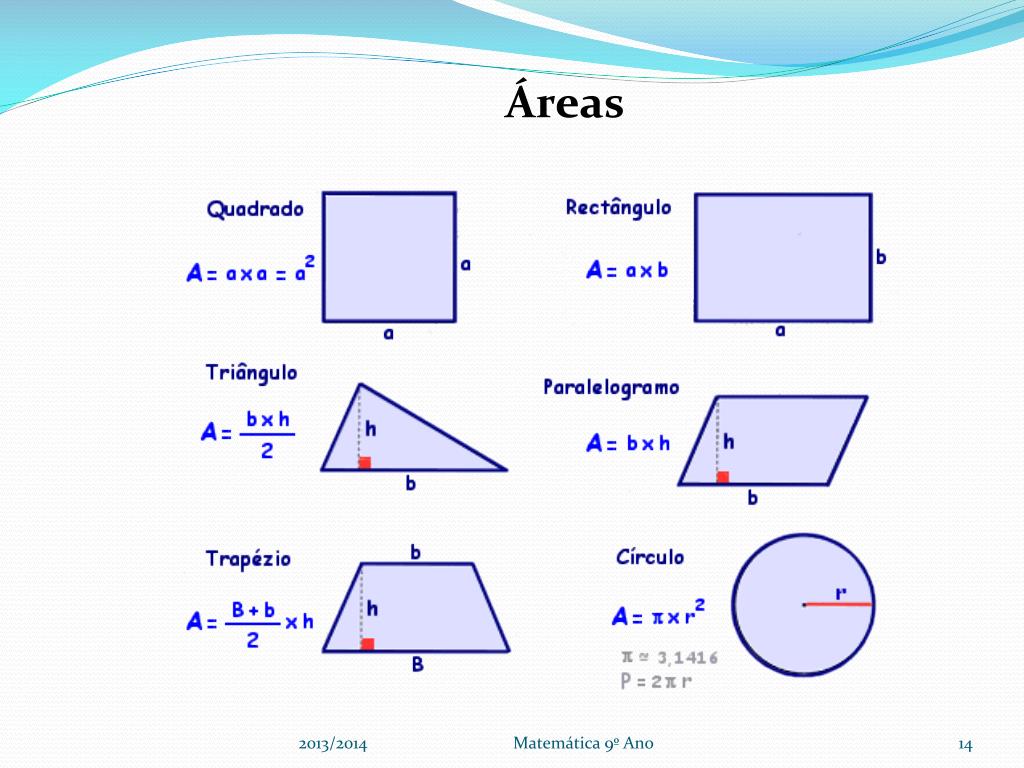 Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.
Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении. Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Формулы для нахождения площади любого треугольника представлены несколькими вариантами:
1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:
2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.
На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:
Прямоугольник
Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:
Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении. Такая формула площади прямоугольника имеет вид:
Квадрат
Площадь квадрата определяют как вторую степень длины стороны:
Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник.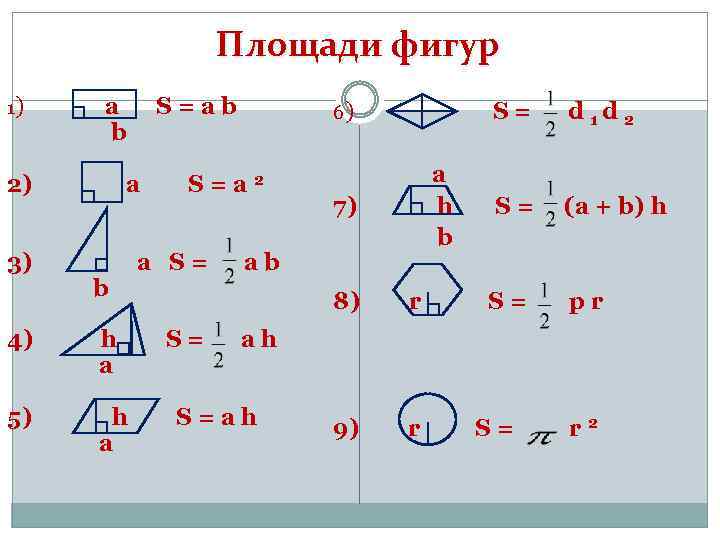 У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
Площадь квадрата можно найти другим способом, например, если использовать диагональ:
Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:
Параллелограмм
Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.
Формулы площади параллелограмма таковы:
Ромб
Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями.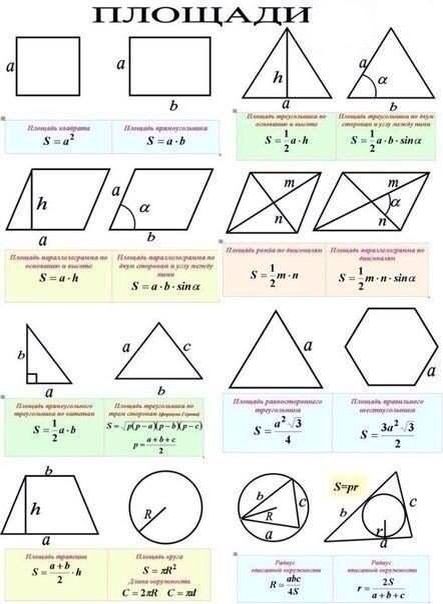 Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:
Трапеция
Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:
Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены.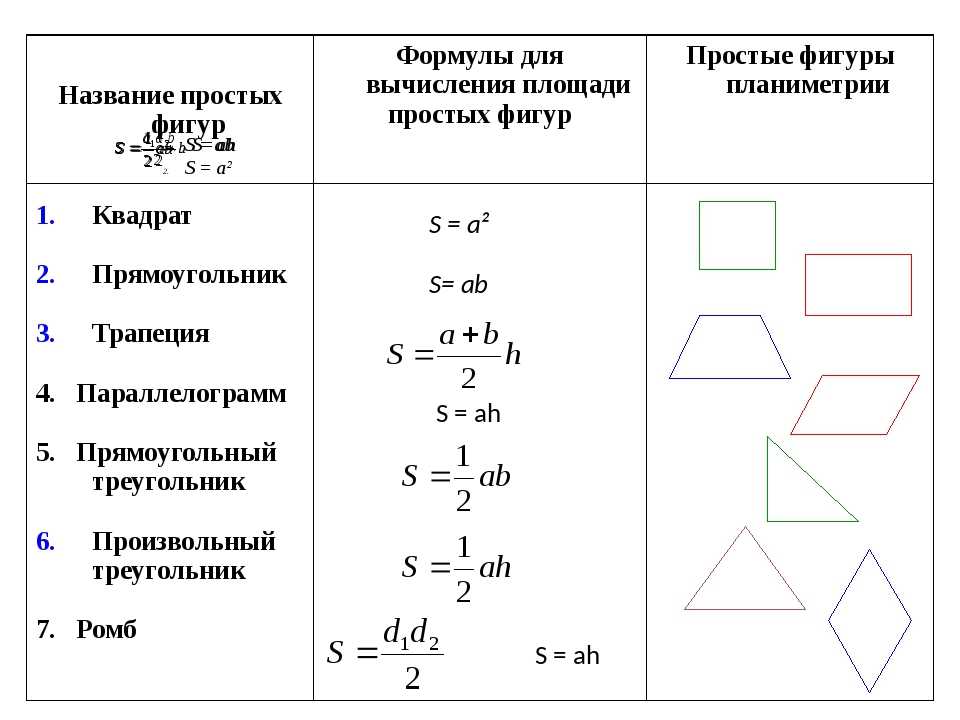 Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
Цилиндр и параллелепипед
Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра. Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:
Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:
Кольцо
Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы. Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Площадь кольца, с использованием длин диаметров, определяют следующим образом:
Многоугольник
Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:
где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.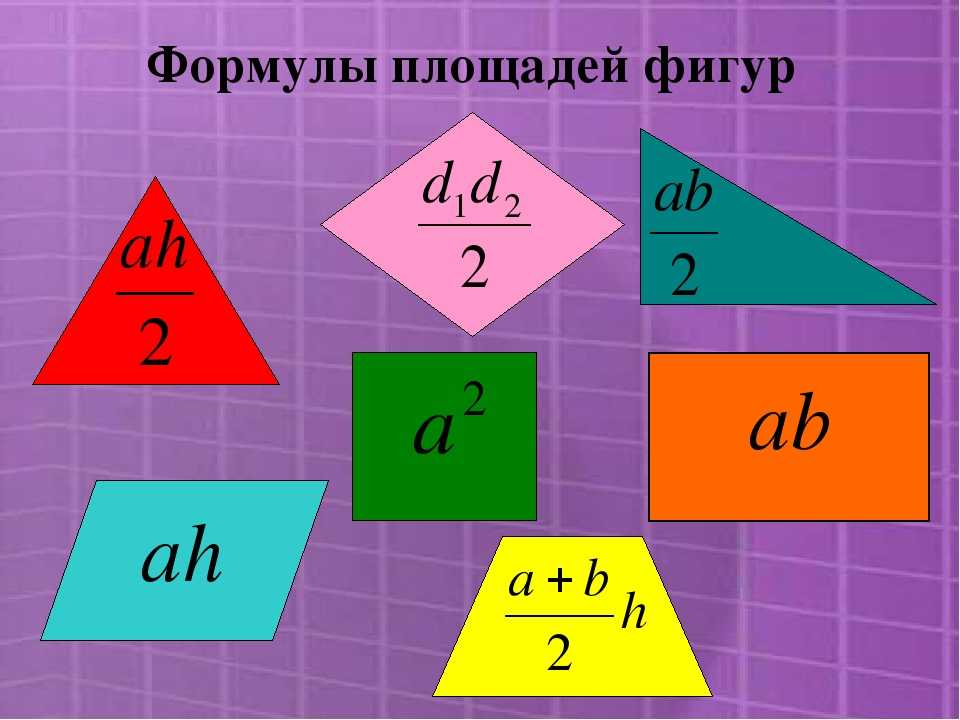
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Как найти площадь фигуры?
Знать и уметь рассчитывать площади различных фигур необходимо не только для решения простых геометрических задач. Не обойтись без этих знаний и при составлении или проверке смет на ремонт помещений, расчета количества необходимых расходных материалов. Поэтому давайте разберемся, как находить площади разных фигур.
Поэтому давайте разберемся, как находить площади разных фигур.
Часть плоскости, заключенная внутри замкнутого контура, называется площадью этой плоскости. Выражается площадь количеством заключенных в ней квадратных единиц.
Чтобы вычислить площадь основных геометрических фигур, необходимо использовать правильную формулу.
Площадь треугольника
Обозначения:
- Если известны h, a, то площадь искомого треугольника определяется как произведение длин стороны и высоты треугольника, опущенной к этой стороне, разделенное пополам: S=(a·h)/2
- Если известны a, b, c, то искомая площадь рассчитывается по формуле Герона: корень квадратный, взятый из произведения половины периметра треугольника и трех разностей половины периметра и каждой стороны треугольника: S = √(p·(p — a)·(p — b)·(p — c)).
- Если известны a, b, γ, то площадь треугольника определяется как половина произведения 2-х сторон, умноженная на значение синуса угла между этими сторонами: S=(a·b·sin γ)/2
- Если известны a, b, c, R, то искомая площадь определяется как деление произведения длин всех сторон треугольника на четыре радиуса описанной окружности: S=(a·b·c)/4R
- Если известны p, r, то искомая площадь треугольника определяется умножением половины периметра на радиус вписанной в него окружности: S=p·r
Площадь квадрата
Обозначения:
- Если известна сторона, то площадь данной фигуры определяется как квадрат длины его стороны: S=a 2
- Если известна d, то площадь квадрата определяется как половина квадрата длины его диагонали: S=d 2 /2
Площадь прямоугольника
Обозначения:
- S — определяемая площадь,
- a, b — длины сторон прямоугольника.
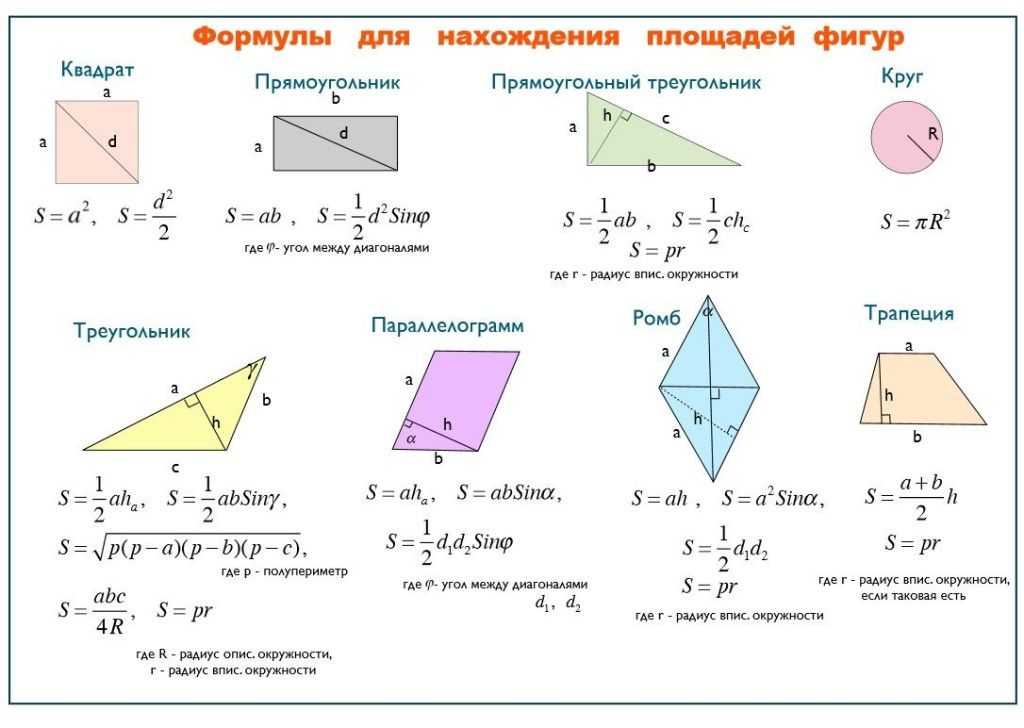
- Если известны a, b, то площадь данного прямоугольника определяется произведением длин двух его сторон: S=a·b
- Если длины сторон неизвестны, то площадь прямоугольника нужно разбить на треугольники. В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.
Площадь параллелограмма
Обозначения:
- S — искомая площадь,
- a, b — длины сторон,
- h — длина высоты данного параллелограмма,
- d1, d2 — длины двух диагоналей,
- α — угол, находящийся между сторонами,
- γ — угол, находящийся между диагоналями.
- Если известны a, h, то искомая площадь определяется перемножением длин стороны и высоты, опущенной на эту сторону: S=a·h
- Если известны a, b, α, то площадь параллелограмма определяется перемножением длин сторон параллелограмма и значения синуса угла между этими сторонами: S=a·b·sin α
- Если известны d 1 , d 2 , γ то площадь параллелограмма определяется как половина произведения длин диагоналей и значения синуса угла между этими диагоналями: S=(d 1 ·d 2 ·sinγ)/2
Площадь ромба
Обозначения:
- S — искомая площадь,
- a — длина стороны,
- h — длина высоты,
- α — меньший угол между двумя сторонами,
- d1, d2 — длины двух диагоналей.

- Если известны a, h, то площадь ромба определяется умножением длины стороны на длину высоты, которая опущена на эту сторону: S=a·h
- Если известны a, α, то площадь ромба определяется перемножением квадрата длины стороны на синус угла между сторонами: S=a 2 ·sin α
- Если известны d 1 и d 2 , то искомая площадь определяется как половина произведения длин диагоналей ромба: S=(d 1 ·d 2)/2
Площадь трапеции
Обозначения:
- Если известны a, b, c, d, то искомая площадь определяется по формуле: S= (a+b) /2 *√ .
- При известных a, b, h, искомая площадь определяется как произведение половины суммы оснований и высоты трапеции: S=(a+b)/2·h
Площадь выпуклого четырехугольника
Обозначения:
- Если известны d 1 , d 2 , α, то площадь выпуклого четырехугольника определяется как половина произведения диагоналей четырехугольника, умноженная на величину синуса угла между этими диагоналями: S=(d 1 · d 2 ·sin α)/2
- При известных p, r площадь выпуклого четырехугольника определяется как произведение полупериметра четырехугольника на радиус окружности, вписанной в этот четырехугольник: S=p·r
- Если известны a, b, c, d, θ, то площадь выпуклого четырехугольника определяется как корень квадратный из произведений разницы полупериметра и длины каждой стороны за минусом произведения длин всех сторон и квадрата косинуса половины суммы двух противоположных углов: S 2 = (p — a)(p — b)(p — c)(p — d) — abcd·cos 2 ((α+β)/2)
Площадь круга
Обозначения:
Если известен r, то искомая площадь определяется как произведение числа π на радиус в квадрате: S=π r 2
Если известна d, то площадь круга определяется как произведение числа π на квадрат диаметра, поделенное на четыре: S=(π·d 2)/4
Площадь сложной фигуры
Сложную можно разбить на простые геометрические фигуры.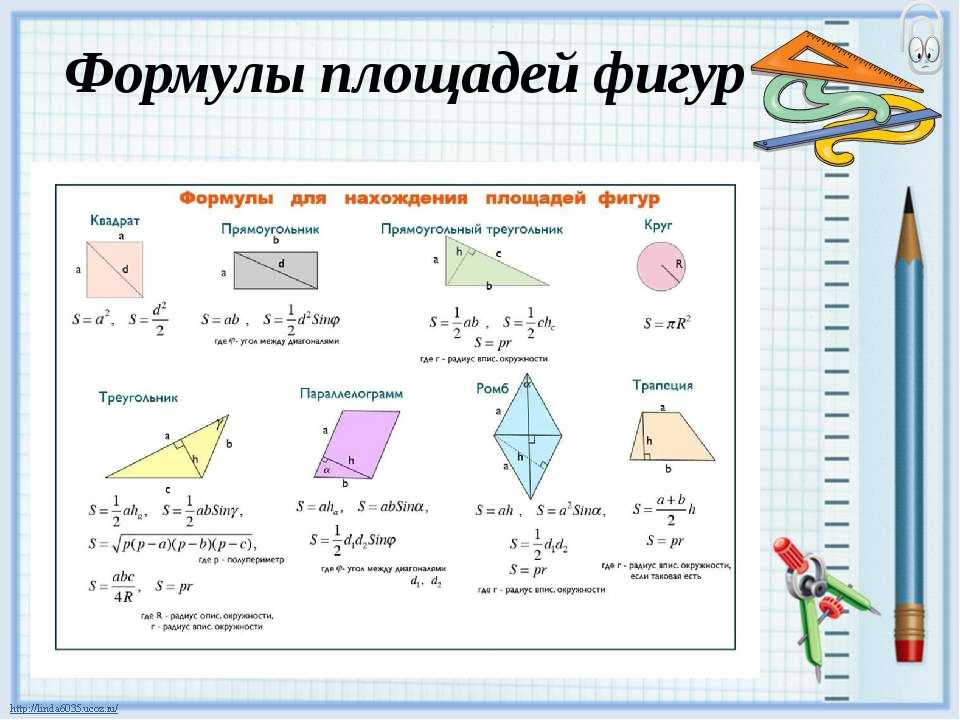 Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо.
Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо.
Обозначение:
- S — площадь кольца,
- R, r — радиусы внешней окружности и внутренней соответственно,
- D, d — диаметры внешней окружности и внутренней соответственно.
Для того чтобы найти площадь кольца, надо из площади большего круга отнять площадь меньшего круга. S = S1-S2 = πR 2 -πr 2 = π (R 2 -r 2).
Таким образом, если известны R и r, то площадь кольца определяется как разница квадратов радиусов внешней и внутренней окружностей, умноженная на число пи: S=π(R 2 -r 2).
Если известны D и d, то площадь кольца определяется как четверть разницы квадратов диаметров внешней и внутренней окружностей, умноженная на число пи: S= (1/4)(D 2 -d 2) π.
Площадь закрашенной фигуры
Предположим, что внутри одного квадрата (А) находится другой (Б) (меньшего размера), и нам нужно найти закрашенную полость между фигурами «А» и «Б».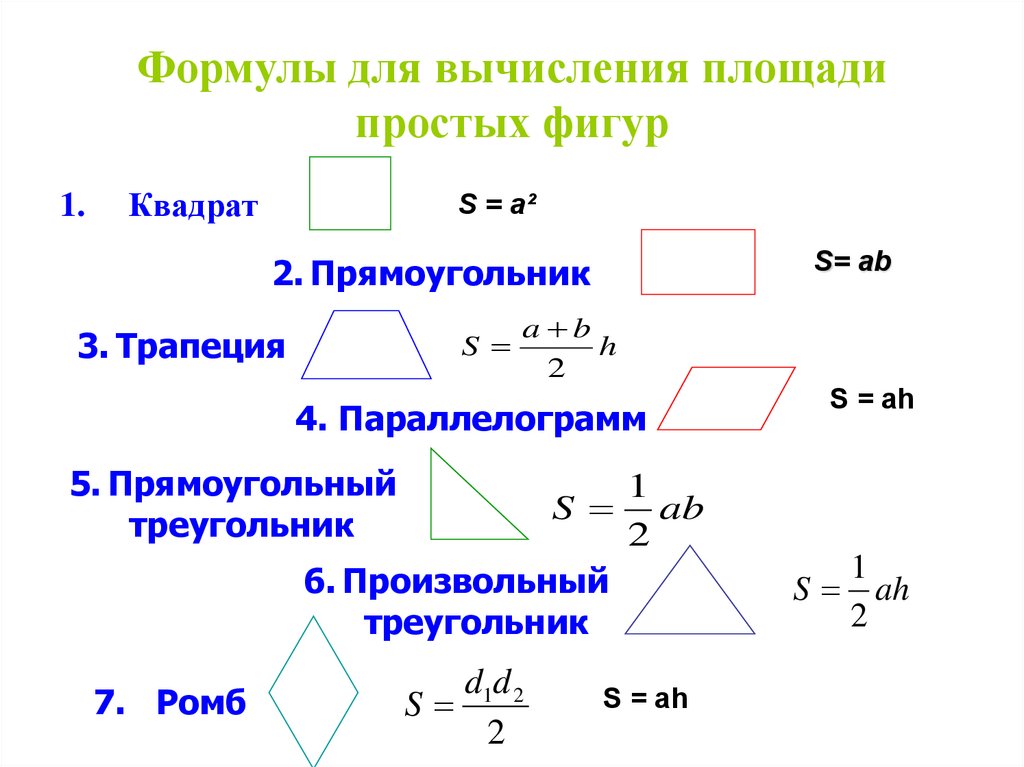 Скажем так, «рамку» маленького квадрата. Для этого:
Скажем так, «рамку» маленького квадрата. Для этого:
- Находим площадь фигуры «А» (вычисляется по формуле нахождения площади квадрата).
- Аналогичным образом находим площадь фигуры «Б».
- Вычитаем из площади «А» площадь «Б». И таким образом получаем площадь закрашенной фигуры.
Теперь вы знаете, как находить площади разных фигур.
Площади фигур — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1.
 Проект по геометрии учеников 8 «Б» класса
Проект по геометрии учеников 8 «Б» класса
S = d2
 Также площадь параллелограмма можно найти через угол между двумя сторонами:
Также площадь параллелограмма можно найти через угол между двумя сторонами:S = a · a sinα = a2 · sinα
3. Площадь ромба через диагонали:
Площадь ромба через диагонали:
S = d1 · d2
Как найти площадь трапеции?
1. Площадь трапеции находится по следующей формуле:
S = · h
Как найти площадь круга?
1. Площадь круга можно найти через радиус:
S = π r2
2. Площадь круга можно найти через диаметр:
S = πd2/4
Площадь | интернет проект BeginnerSchool.ru
В этой статье мы разберемся, как вычислить площадь фигуры.
Сравнить площади разных фигур можно способом наложения. Посмотрите на рисунок. Мы видим две фигуры: треугольник и прямоугольник. Для того, чтобы их сравнить мы можем наложить меньшую фигуру на большую. Треугольник полностью поместился в прямоугольнике, это значит, что треугольник меньше прямоугольника.
Посмотрите на рисунок. Мы видим две фигуры: треугольник и прямоугольник. Для того, чтобы их сравнить мы можем наложить меньшую фигуру на большую. Треугольник полностью поместился в прямоугольнике, это значит, что треугольник меньше прямоугольника.
Но не всегда можно сравнить площади фигур таким способом. Тогда можно разбить фигуру на равные квадраты и посчитать количество квадратов входящих в эту фигуру.
На рисунке изображено две фигуры. Путем наложения эти фигуры сравнить невозможно. Мы разбили эти фигуры на квадраты с одинаковой площадью. Теперь можно посчитать количество квадратов входящих в эти фигуры. В первую фигуру вписалось 6 квадратов, а во вторую 8. Значит площадь первой фигуры меньше площади второй.
Площадь фигуры равна числу единичных квадратов, составляющих эту фигуру.
Если у квадрата сторона равна 1 см, то площадь такого квадрата равна 1 квадратному сантиметру (см2).
Площадь квадрата сторона которого равна 1 дециметр равна 1 квадратному дециметру (дм2) или 100 квадратным сантиметрам(см2).
Площадь фигуры обозначается заглавной латинской буквой S.
Допустим нам надо найти площадь прямоугольника, длины сторон которого равны 6 и 4 см. Разделим прямоугольник на квадратные сантиметры и вычислим его площадь.
Итак, умножим длину прямоугольника на его ширину и получим площадь:
S = 6 × 4 = 24 см2
Чтобы вычислить площадь прямоугольника, надо измерить его длину и ширину в одинаковых единицах измерения и найти их произведение.
Если известна площадь прямоугольника и ширина, то найти длину просто, надо разделить площадь на известную длину.
Д = S ÷ Ш
или
Ш = S ÷ Д
Например, площадь прямоугольника равна 15 см2. Длина прямоугольника равна 5 см. Найдем его ширину:
Ш = 15 ÷ 5 = 3 см
Если фигура сложная, например, такая как на рисунке, то вычислить её площадь можно разбив фигуру на прямоугольники, вычислить их площадь, а затем сложить полученные площади.
Итак нашу фигуру мы можем разбить на два прямоугольника: первый площадью 2 см2, и второй площадью 8 см2:
S = 2 × 1 + 4 × 2 = 10 см2
А как найти площадь прямоугольного треугольника. Для этого надо достроить треугольник до прямоугольника, так как показано на рисунке.
Для этого надо достроить треугольник до прямоугольника, так как показано на рисунке.
Теперь найдем площадь полученного прямоугольника и разделим её пополам:
S = (3 × 6) ÷ 2 = 9 см2
Кажется все просто, когда треугольник прямоугольный. Если у треугольника нет прямого угла, то вычислить его площадь можно следующим образом:
На следующем рисунке мы видим треугольник, площадь которого нам надо вычислить, он выделен желтым цветом. Впишем его в прямоугольник, так как показано на рисунке. Длина полученного прямоугольна – 5 см. Ширина – 4 см. Вершина треугольника делит длину прямоугольника на части в 3 и 2 см.
Теперь для того, чтобы найти площадь нашего треугольника, надо вычислить площади двух полученных прямоугольных треугольников и сложить их:
S1 = (3 × 4) ÷ 2 = 6 см2
S2 = (2 × 4) ÷ 2 = 4 см2
S = S1 + S2 = 6 + 4 = 10 см2
Спасибо, что Вы с нами.
Понравилась статья — поделитесь с друзьями:
Оставляйте пожалуйста комментарии в форме ниже
Площади фигур.
 Сравнение площадей фигур
Сравнение площадей фигур


 На глаз.
На глаз. Назовите второй способ сравнения фигур?
Назовите второй способ сравнения фигур?4. Закрепление

 Обратите внимание, что периметр окружности часто называют длиной.
Обратите внимание, что периметр окружности часто называют длиной.P:
 д.
д.Узнайте больше о площади или воспользуйтесь калькулятором площади.

w = ширина
h = высота
 При взгляде сбоку он имеет основание 20 м и высоту 14 м.
При взгляде сбоку он имеет основание 20 м и высоту 14 м.  Другими словами, его можно определить как пространство, занимаемое плоской формой.Чтобы понять концепцию, обычно полезно рассматривать площадь как как количество краски, необходимое для покрытия поверхности . Посмотрите на картинку ниже — все фигуры имеют одинаковую площадь, 12 квадратных единиц:
Другими словами, его можно определить как пространство, занимаемое плоской формой.Чтобы понять концепцию, обычно полезно рассматривать площадь как как количество краски, необходимое для покрытия поверхности . Посмотрите на картинку ниже — все фигуры имеют одинаковую площадь, 12 квадратных единиц: 
A = a² A = a * b -
A = b * h / 2или -
А = 0.5 * a * b * sin (γ)или -
A = 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))или -
A = a² * sin (β) * sin (γ) / (2 * sin (β + γ))
A = πr² A = r² * угол / 2 A = a * b * π A = (a + b) * h / 2 -
A = a * hили -
A = a * b * sin (угол)или -
A = e * f * sin (угол)
-
A = a * hили -
A = (e * f) / 2или -
A = s² * sin (угол)
-
A = (e * f) / 2или -
A = a * b * sin (γ)
A = a² * √ (25 + 10√5) / 4 A = 3/2 * √3 * a² A = 2 * (1 + √2) * a² A = π (R² - r²) A = e * f * sin (угол) A = n * a² * детская кроватка (π / n) / 4 
Площадь квадрата = a * a = a² , где a — сторона квадрата 
Площадь треугольника = b * h / 2 Площадь треугольника = 0.5 * а * б * sin (γ) Площадь треугольника = 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)) Площадь треугольника = a² * sin (β) * sin (γ) / (2 * sin (β + γ))  В этом случае основание и высота — это две стороны, которые образуют прямой угол. Тогда площадь прямоугольного треугольника может быть выражена как:
В этом случае основание и высота — это две стороны, которые образуют прямой угол. Тогда площадь прямоугольного треугольника может быть выражена как: Площадь прямоугольного треугольника = a * b / 2 Площадь круга = πr² , где r — радиус окружности Площадь круга = πr² = π * (d / 2) ² α / 360 ° = Площадь сектора / Площадь круга 360 ° = 2π α / 2π = Площадь сектора / πr² Площадь сектора = r² * α / 2 πr² . Для эллипса у вас есть не одно значение радиуса, а два разных значения:
Для эллипса у вас есть не одно значение радиуса, а два разных значения: a и b . Единственная разница между формулой площади круга и эллипса заключается в замене r² произведением большой и малой полуосей, a * b : Площадь эллипса = π * a * b Площадь трапеции = (a + b) * h / 2 , где a и b — длины параллельных сторон, а h — высота Площадь трапеции = м * ч , где м — среднее арифметическое длин двух параллельных сторон  В нашем инструменте вы найдете три формулы площади параллелограмма:
В нашем инструменте вы найдете три формулы площади параллелограмма: Площадь параллелограмма = a * h Площадь параллелограмма = a * b * sin (α) Площадь параллелограмма = e * f * sin (θ) Площадь ромба = (e * f) / 2 Площадь ромба = a² * sin (α) Площадь змеевика = a * b * sin (α) Площадь пятиугольника = a² * √ (25 + 10√5) / 4 , где a — сторона правильного пятиугольника 
Площадь шестиугольника = 3/2 * √3 * a² , где a — сторона правильного шестиугольника Площадь равностороннего треугольника = (a² * √3) / 4 Площадь шестиугольника = 6 * Площадь равностороннего треугольника = 6 * (a² * √3) / 4 = 3/2 * √3 * a² Площадь восьмиугольника = 2 * (1 + √2) * a² Площадь восьмиугольника = периметр * апофема / 2 8 * . А что такое апофема? Апофема — это расстояние от центра многоугольника до середины стороны. В то же время это высота треугольника, образованного линией от вершин восьмиугольника к его центру. Этот треугольник — один из восьми совпадающих — является равнобедренным треугольником, поэтому его высоту можно рассчитать, например, с помощью теоремы Пифагора по формуле:
А что такое апофема? Апофема — это расстояние от центра многоугольника до середины стороны. В то же время это высота треугольника, образованного линией от вершин восьмиугольника к его центру. Этот треугольник — один из восьми совпадающих — является равнобедренным треугольником, поэтому его высоту можно рассчитать, например, с помощью теоремы Пифагора по формуле: h = (1 + √2) * a / 4 Площадь восьмиугольника = периметр * апофема / 2 = (8 * a * (1 + √2) * a / 4) / 2 = 2 * (1 + √2) * a² Площадь кольца = πR² - πr² = π (R² - r²) 
Площадь четырехугольника = e * f * sin (α) , где e, f — диагонали sin (угол) = sin (180 ° - угол) . Площадь правильного многоугольника = n * a² * детская кроватка (π / n) / 4  Вы можете найти эти формулы в специальном абзаце нашего калькулятора площади многоугольника.
Вы можете найти эти формулы в специальном абзаце нашего калькулятора площади многоугольника. Площадь квадрата = Сторона × Сторона
Площадь = S × S
Площадь = 4 × 4 = 16 кв. размеры в см
размеры в см
Площадь прямоугольника = длина × ширина
= длина × ширина
Площадь = 8 × 3 = 24 кв. См
 14
14  Расчет площади формы или поверхности может быть полезен в повседневной жизни — например, вам может потребоваться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы засеять лужайку.
Расчет площади формы или поверхности может быть полезен в повседневной жизни — например, вам может потребоваться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы засеять лужайку. Другими словами, каждый квадрат сетки равен одному квадратному сантиметру.
Другими словами, каждый квадрат сетки равен одному квадратному сантиметру. 





 8 × 11,6) ÷ 2 = 33,64 м 2
8 × 11,6) ÷ 2 = 33,64 м 2 
 142 × 5 × 5 = 78,55 см 2 .
142 × 5 × 5 = 78,55 см 2 . 
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м 2 .

См. Нашу страницу Оценка, приближение и округление .
Введение
Квадрат и прямоугольники,
Звезды и треугольники.
Вы используете множество предметов разной формы в повседневной жизни и на работе.
 Вот загружаемый PDF-файл, чтобы узнать больше.
Вот загружаемый PDF-файл, чтобы узнать больше. Загрузить

Квадрат

Треугольник
Теперь высоту треугольника можно измерить, проведя прямую (прямоугольную) линию от основания треугольника до вершины (верхнего угла треугольника).

Первый шаг: нам нужно рассчитать площадь обеих пицц. Для этого мы рассмотрим радиус его диаметра, поскольку пицца имеет форму круга.

кв.
3,142 × 10 2 по формуле.
т.е. π × R 2
Площадь будет:
314,2 кв. См.
3,142 × 16 2 =
804.352 кв. См.
Итак, доля Джини составляет 314.2/6 × 4 = 209,466 кв. См.
Его доля составит 804,352 / 6 × 3 = 402,176 кв. См.

Таким образом, площадь окна будет 3 фута × 4 фута = 12 футов.

Форма
Чертеж
Формула
Площадь
a² («a» обозначает длину одной стороны квадрата)
Прямоугольник
Длина × Ширина
Треугольник
½ (основание × высота)
Круг
π x R 2 («π» означает — 3.142 & «R» означает — Радиус окружности)


Что такое площадь?
Методы сетки
Какие бывают типы фигур?
 Е. (Длина x высота) / 2
Е. (Длина x высота) / 2 Какова площадь квадрата?
Калькулятор площади

А = а × а
w = ширина
w1 = внешняя ширина
l2 = внутренняя длина
w2 = внутренняя ширина
b = основание b
h = высота
h = высота
A = s (s — a) (s — b) (s — c))
b = край b
c = край c
 Вы также можете использовать упрощенную формулу, если известна высота треугольника.
Вы также можете использовать упрощенную формулу, если известна высота треугольника. h = высота
b = ось b
θ = угол
n = количество сторон

тот же периметр:

треугольник, квадрат, шестиугольник и круг?
площадь, ограниченная фигурой с фиксированным периметром.Здесь рассматриваются только три формы, потому что проблема сложна для более неправильных форм. Для
Например, из всех треугольников тот, у которого фиксированный периметр $ P $ и наибольшая площадь
равносторонний треугольник, все стороны которого равны $ frac {P} {3} $, но это
трудно показать, потому что нелегко найти площадь треугольника в терминах
длины трех сторон (хотя формула Герона позволяет это сделать). Ни
легко ли сравнить площадь двух треугольников с одинаковым периметром без
зная свои индивидуальные области.
 Для четырехугольников возникает аналогичная проблема:
Для четырехугольников возникает аналогичная проблема:показывая, что из всех прямоугольников с периметром $ P $ тот, у которого наибольший
Площадь — квадрат, длина сторон которого равна $ frac {P} {4} $ — хорошая задача, над которой должны подумать учащиеся. Но сравнить квадрат с четырехугольником неправильной формы равного периметра будет сложно.
возможность для студентов попрактиковаться, используя свои знания различных
геометрические формулы для площади и периметра.Учитель, чтобы подкрепить
часть (d), возможно, пожелает нарисовать примеры шестиугольника и восьмиугольника (оба разделяют
тот же периметр, что и у других фигур). Основная идея заключается в том, что по мере увеличения количества сторон многоугольника многоугольник становится все больше и больше похож на круг, и, в частности, его площадь приближается к площади круга.
 ruРазное
ruРазное
 Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так: Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:


 Поэтому давайте разберемся, как находить площади разных фигур.
Поэтому давайте разберемся, как находить площади разных фигур.

 Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо.
Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо. Скажем так, «рамку» маленького квадрата. Для этого:
Скажем так, «рамку» маленького квадрата. Для этого: Проект по геометрии учеников 8 «Б» класса
Проект по геометрии учеников 8 «Б» классаКалинина Даниила
И
Самошкина Артема
2. Тема проекта: «Площади фигур»
3. Тип проекта: Информационный
4. Цель проекта: « Ознакомиться с формулами по нахождению площади в разных фигурах».
5. Источники информации: -Учебная литература -Интернет ресурсы
6. З а д а ч и п р о е к т а :
З адач и
прое кт а :
А) Познакомиться с формулами S
треугольника
Б)Познакомиться с формулами S квадрата
В)Познакомиться с формулами S
прямоугольника
Г)Познакомиться с формулами S
параллелограмма
Д)Познакомиться с формулами S ромба
Е) Познакомиться с формулами S трапеции
Ж) Познакомиться с формулами S
Выпуклого четырехугольника
З) Познакомиться с формулами S
круга
И) Познакомиться с формулами S
эллипса
7. Формулы площади треугольника
1)Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину
проведенной к этой стороне высоты
S =1/2 a · h
2)Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
3)Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус
угла между ними.
S = 1/2 a · b · sin γ
4)Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = (a · b · с)/4R
5)Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной
окружности. S = p · r
где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,
p = (a + b + c) /2 — полупериметр треугольника.
9. Формулы площади квадрата
1)Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
S = a2
2)Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его
диагонали.
S = 1/2 d2
где S — Площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.
10. Задача
Найти площадь квадрата
Дано: ABCD – квадрат
Сторона A
A = 5 см
Найти: S ABCD
Решение :
S= a2
S= 52 =25см2
Ответ: S =25см2
A
B
C
D
11.
 Формула площади прямоугольникаПлощадь прямоугольника равна произведению длин
Формула площади прямоугольникаПлощадь прямоугольника равна произведению длин
двух его смежных сторон
S=a·b
где S — Площадь прямоугольника,
a, b — длины сторон прямоугольника.
12. Задача
Найти площадь прямоугольника.
Дано: прямоугольник со сторонами a и b,
a = 4 см, b = 2 см.
Найти: S.
Решение:
S = ab
S = 4 см ∙ 2 см = 8 см2
Ответ: S = 8 см2
13. Формулы площади параллелограмма
1)Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и
длины опущенной на эту сторону высоты.
S=a·h
2)Формула площади параллелограмма по двум сторонам и углу
между ними
Площадь параллелограмма равна произведению длин его сторон
умноженному на синус угла между ними.
S = a · b · sin α
3)Формула площади параллелограмма по двум диагоналям и углу
между ними
Площадь параллелограмма равна половине произведения длин его
диагоналей умноженному на синус угла между ними.
S = 1/2 d1 d2 · sin γ
где S — Площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.
14. Задача
Найти площадь параллелограмма
Дано: параллелограмм ABCD,
BH – высота
AD = 8 см,
BH = 5 см.
Найти: S ABCD
Решение:
S = AD ∙ BH
S = 8 см ∙ 5 см = 40 см2
Ответ: S = 40 см2
15. Формулы площади ромба
1)Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины
опущенной на эту сторону высоты.
S=a·h
2)Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его
стороны и синуса угла между сторонами ромба.
S = a2 · sin α
3)Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его
диагоналей.
S = 1/2d1 · d2
где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d1, d2 — длины диагоналей.
16. Задача
Найти площадь ромба
Дано:ABCD-ромб
AC=10см
BD=24см
AC,BD-диагонали
Найти:S ABCD
Решение:
S ABCD = ½ d1 · d2
S ABCD = ½ · 10 ·24 =120см2
Ответ: S = 120см2
17. Формулы площади трапеции
1)Формула Герона для трапеции
S = (a + b) · √(p — a)(p — b)(p — a — c)(p — a — d)
|a — b|
2)Формула площади трапеции по длине основ и
высоте
Площадь трапеции равна произведению полусуммы ее
оснований на высоту
S = 1/2(a + b) · h
где S — Площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d — полупериметр трапеции.
2
18. Задача
Найти площадь трапеции
Дано: трапеция ABCD,
BC = 4 см, AD = 6 см
BH = 5 см.
Найти: S.
Решение:
S = ½(AD + BC) ∙ BH
S = ½(4 см + 6 см) ∙ 5 см = ½ ∙ 10 см ∙ 5 см = ½ ∙ 50 см2 = 25см2
Ответ: S = 25 см2
19.
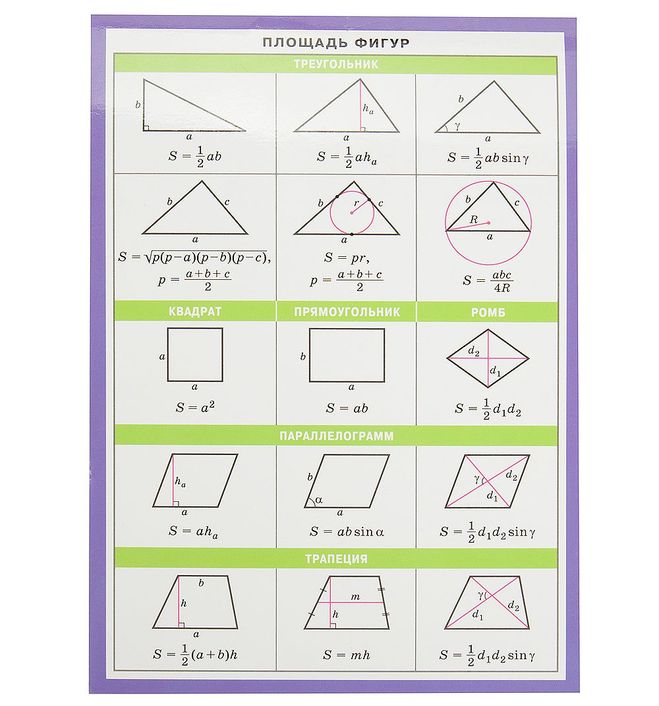 Формулы площади выпуклого четырехугольника1)Формула площади четырехугольника по длине диагоналей и углу между ними
Формулы площади выпуклого четырехугольника1)Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на
синус угла между ними:
S = 1/2d1 d2 sin α
где S — площадь четырехугольника,
d1, d2 — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника.
2)Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной
окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной
окружности
S=p·r
3)Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d — полупериметр четырехугольника,
2
θ = α + β — полусумма двух противоположных углов четырехугольника.
2
4)Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p — a)(p — b)(p — c)(p — d)
20.
 ЗадачаНайти площадь выпуклого четырехугольника
ЗадачаНайти площадь выпуклого четырехугольника
Дано:ABCD-выпуклый четырехугольник
d1 и d2- диагонали
d1=2 d2= 5
Угол α = 30
sin α=1/2
Найти: S ABCD
Решение:
S = 1/2d1 d2 sin α
S = 1/2 ∙2 ∙5 ∙ 1/2 =2,5см2
Ответ: S = 2,5см2
21. Формулы площади круга
1)Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на
число пи.
S = π r2
2)Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата
диаметра на число пи.
S = 1π d2
4
где S — Площадь круга,
r — длина радиуса круга,
d — длина диаметра круга.
22. Задача
Найти площадь круга
Дано: Окр(О;r=2)
π =3.14
Найти:S окружности
Решение:
S = π r2
S =3.14 ∙ 22 =12.56 см2
Ответ: S =12.56 см2
23. Формулы площади эллипса
Площадь эллипса равна произведению длин
большой и малой полуосей эллипса на число пи.
S=π·a·b
где S — Площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
24. Задача
Найти площадь эллипса
Дано: Эллипс
π=3,14
a=2 см b=3 см
Найти:S эллипса
Решение:
S=π·a·b
S = 3,14 · 2 ·3=18,84 см2
Ответ: S =18,84 см2
25. The END
English
Русский
Правила
Формулы площадей всех фигур в геометрии — примеры вычислений
Площадь — это одна из наиболее важных и неотъемлемых характеристик любой замкнутой геометрической фигуры, показывающая её размер. Она может измеряться в различных единицах: квадратных миллиметрах, сантиметрах, дециметрах, метрах и так далее. Это своеобразный аналог объёма трёхмерных фигур (шара, цилиндра, конуса и других). В геометрии разработаны формулы площадей. Их доказательством являются соответствующие теоремы. Существует общепринятое обозначение площади — буква S (от англ. square).
Содержание
- Формулы для треугольников
- Площадь четырёхугольников
- Квадрат и прямоугольник
- Параллелограмм, ромб и трапеция
- Выпуклый четырёхугольник
- Круг и эллипс
Формулы для треугольников
Имеется несколько формул площади треугольника.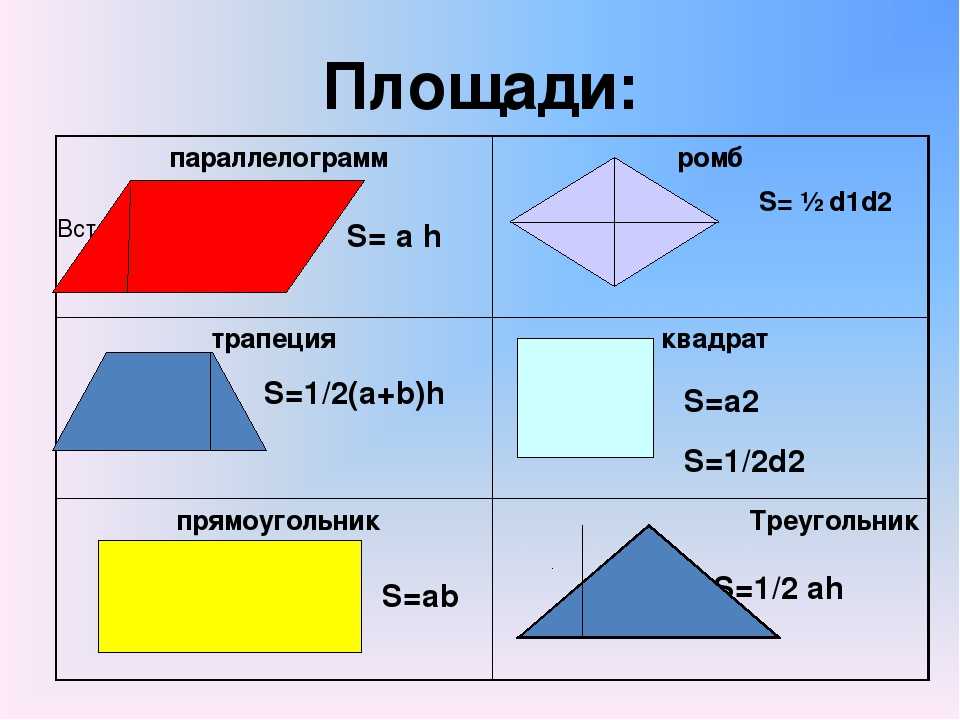 Если в треугольнике известны две величины: во-первых, длина стороны, а во-вторых, высота, опущенная из противоположного угла перпендикулярно этой стороне, то площадь можно определить, умножив длину на высоту и разделив полученное произведение на два. Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.
Если в треугольнике известны две величины: во-первых, длина стороны, а во-вторых, высота, опущенная из противоположного угла перпендикулярно этой стороне, то площадь можно определить, умножив длину на высоту и разделив полученное произведение на два. Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.
При известности всех трёх сторон — a, b, c, широко применяется формула, названная в честь Герона — математика из Древней Греции: S = √(p*(p — a)*(p — b)*(p — c)). Величина p — это половина от периметра треугольника (полупериметр). Чтобы его рассчитать, необходимо суммировать все стороны и разделить сумму на два: (a + b + c)/2.
Для ещё одной формулы требуются следующие данные:
- длина двух соприкасающихся в одной вершине сторон — a и b;
- градус угла, который образуют эти стороны.
Тогда расчёт можно произвести таким способом: S = ½ * a * b * sin γ. Синус угла является одной из тригонометрических функций, представляющей собой результат деления (отношение) в прямоугольном треугольнике противолежащего (дальнего) катета к гипотенузе (сторона напротив прямого угла). Значение sin γ для конкретного угла можно посмотреть в специальной таблице.
Синус угла является одной из тригонометрических функций, представляющей собой результат деления (отношение) в прямоугольном треугольнике противолежащего (дальнего) катета к гипотенузе (сторона напротив прямого угла). Значение sin γ для конкретного угла можно посмотреть в специальной таблице.
Когда два треугольника являются подобными (подобие означает, что у них равны углы и стороны пропорциональны), то отношение их площадей соответствует отношению возведённых в квадрат сторон. Такое отношение сторон для них (например, AB: A (1) B (1)) именуется коэффициентом подобия (k). Поэтому отношение площадей равняется коэффициенту подобия в квадрате.
Если в треугольнике даны все стороны, тогда, кроме формулы Герона, есть возможность воспользоваться ещё одним способом. Он основан на том, что можно вписать любой треугольник в круг. Зная такую величину, радиус ® окружности и три стороны треугольника, производится расчёт: S = (a * b * c) / 4 R.
В любой треугольник: равносторонний и разносторонний, остроугольный и тупоугольный, в силу его геометрических свойств также может быть вписана окружность.
В таком случае формула нахождения площади следующая: S = p * r. Буква p обозначает ½ периметра треугольника, r — это радиус окружности.
Площадь четырёхугольников
Четырёхугольник — это одна из фигур в геометрии (многоугольник), имеющая четыре стороны, а также четыре вершины, три из которых не находятся на одной прямой. Четырёхугольник называется выпуклым, если он располагается по одну сторону относительно прямой, являющейся продолжением любой из его сторон.
К выпуклым четырёхугольникам относятся практически все известные фигуры, имеющие четыре вершины, а также четыре стороны. Основными их видами выступают: 1) ромб; 2) прямоугольник; 3) трапеция; 4) квадрат; 5) параллелограмм.
Квадрат и прямоугольник
Самый простой способ вычисления площади квадрата — умножить сторону «саму на себя», иными словами, возвести в квадрат длину любой из его сторон (S = a2 ). Такой расчёт обусловлен особым признаком квадрата — тем, что все его стороны являются абсолютно равными между собой, поэтому квадрат называется правильной фигурой.
Такой расчёт обусловлен особым признаком квадрата — тем, что все его стороны являются абсолютно равными между собой, поэтому квадрат называется правильной фигурой.
Существует вторая, более сложная, формула площади квадрата, где осуществляется расчёт через диагональ. Диагональ — это линия, соединяющая в фигуре два угла, друг другу противоположных. Для определения площади необходимо длину диагонали возвести в квадрат и полученный результат разделить на два: S = ½ d 2.
Для прямоугольника используется формула: S = a * b, где a, b — длина двух разных, имеющих общую вершину, сторон.
Параллелограмм, ромб и трапеция
Параллелограмм представляет собой четырёхугольник, в котором имеются два противоположных друг другу тупых угла и два — острых.
Применяются три формулы площади параллелограмма:
- Умножить сторону на высоту, перпендикулярную стороне: S = a * h.

- Перемножить две, выходящих из одной вершины, стороны параллелограмма, и умножить на синус угла, образованного ими: S = a * b * sin γ.
- Перемножить диагонали фигуры, затем умножить на синус угла, образованного диагоналями, и разделить результат на два: S = ½ d (1) * d (2) * sin γ.
Ромб похож на параллелограмм с одним отличием: он является равносторонним. Поэтому для вычисления площади ромба используются похожие формулы:
Трапеция является геометрической фигурой, имеющей такие элементы: два параллельных основания — верхнее и нижнее, две боковые стороны, расположенные к нижнему основанию под острым углом. Что касается боковых сторон, то они могут быть как равными по длине (так называемая равнобедренная трапеция), так и разными.
Что касается боковых сторон, то они могут быть как равными по длине (так называемая равнобедренная трапеция), так и разными.
В связи с тем, что в «составе» трапеции можно «выделить» прямоугольник и два расположенных по бокам от него треугольника, то можно определить площадь по специальной формуле Герона: S = (a + b): | a + b | * √(p — a) * (p — b) * (p — a — c) * (p — a — d).
В этой формуле имеются следующие обозначения:
- буквы a, b — это основы трапеции,
- буквы c, d — стороны,
- p — полупериметр.
Выпуклый четырёхугольник
В отношении всех иных выпуклых четырёхугольников, то есть имеющих разные по длине стороны и разные углы, разработаны свои формулы вычисления площади.
Прежде всего, можно перемножить две диагонали, а также синус образуемого ими угла, разделив общий результат на два, то есть применить формулу: S = ½ d (1) * d (2) * sin γ.
В том случае, когда внутри выпуклого четырёхугольника, так же как и внутри треугольника, может быть вписан круг, то для нахождения площади четырёхугольной фигуры, требуется определить две величины:
- r — радиус окружности;
- p — ½ периметра четырёхугольника.

После чего полупериметр умножается на радиус. Это и будет площадь четырёхугольника. Формула выглядит так: S = p * r.
Для тех случаев, когда круг может быть очерчен вокруг четырёхугольника, применяется другая формула. Для её использования все стороны фигуры должны быть известны. Они обозначаются буквами a, b, c, d. Рассчитывается половина периметра: p = (a + b + c + d)/2. Затем определяется площадь: S = √(p — a)(p — b)(p — c)(p — d).
Когда конфигурация четырёхугольника такова, что не позволяет возле него описать круг, то в связи с этим формула площади немного дополняется: S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2 γ.
Коэффициент γ представляет собой половину от суммы двух противоположных углов четырёхугольной фигуры: γ = (угол (1) + угол (2)) / 2.
Круг и эллипс
Самое распространённое и широко применяемое правило определения площади круга — это умножение радиуса окружности в квадрате на число пи: S = π * r 2.
Число пи, обозначаемое греческой буквой «π» — это математическая постоянная, которая является результатом деления длины окружности на диаметр. π — иррациональное число. Для расчётов признаётся его среднее значение, равное 3,14.
Вместо радиуса можно использовать диаметр окружности: диаметр возводится в квадрат, умножается на число π, результат делится на четыре. Формула выглядит так: S = (π * d 2) / 4.
Для того чтобы посчитать площадь такой фигуры, как эллипс, необходимо провести две оси, то есть две линии, каждая из которых разделяет эллипс на две равные части, при этом сами линии перпендикулярны друг другу (образуют прямой угол). Точка пересечения разделяет каждую из осей напополам, образуя полуоси.
Площадь эллипса вычисляется как произведение трёх величин: числа π, длины большой полуоси (а) и длины малой полуоси (b): S = π * a * b. Для удобства расчёта площадей различных фигур также можно использовать специальные онлайн-калькуляторы.
Довольно точно можно вычислить площадь прямоугольной фигуры, но для фигуры неправильной формы можно найти её приближённую площадь. Для этого удобно использовать палетку.
Палетка — это прозрачная плёнка (или калька), расчерченная на равные квадраты со стороной (1) см.
Самостоятельно сделай палетку.

С её помощью ты сможешь быстро находить приближённую площадь разных фигур.
Для нахождения приближённой площади фигуры нужно:
1) наложить палетку на фигуру;
2) посчитать число (a) целых клеток внутри фигуры;
3) посчитать количество (b) клеток, частично входящих в фигуру;
4) вычислить приближённую площадь
S≈a+b:2
.
Поясним также, зачем нужно делить (b) на два.
(b) — число клеток, частично входящих в фигуру. У одних большая часть входит в фигуру, у других — меньшая. Из них можно составить приближённо (b:2) полных клеток (если (b) нечётно, то можно сначала увеличить (b) на (1), а потом уже разделить на (2)).
Обрати внимание!
Для записи приближённого равенства используется знак
≈
.
Найдём с помощью палетки приближённую площадь фигуры (B) неправильной формы.
1. Наложим палетку на фигуру (B).

2. Посчитаем количество (a) клеток, целиком находящихся внутри фигуры (закрашены зелёным цветом):

3. Посчитаем количество (b) клеток, частично входящих в фигуру (B) (закрашены синим). Таких клеток (17) — это нечётное число, поэтому увеличим это число на (1) и поделим на (2):
17+1=18,18:2≈9.
4. Сложим числа, полученные в пунктах (2) и (3), и запишем приближённую площадь фигуры (B):
S≈16+9=25см2.
Обрати внимание!
Нужно понимать разницу между оценкой площади и нахождением её приближённого значения!
Оценка площади записывается неравенством
a<S<b
.
Приближённое значение площади — это число, которое можно найти по формуле
S≈a+b:2
.
Источники:
Изображение: палетка. © ЯКласс.
Изображения: фигура. © ЯКласс.
