На практике часто возникают задачи, которые требуют умения строить сечения геометрических фигур различной формы и находить площади сечений. В данной статье рассмотрим, как строятся важные сечения призмы, пирамиды, конуса и цилиндра, и как рассчитывать их площади.
Объемные фигуры
Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.

Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.
Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).
Цилиндр
Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.

Для этой фигуры существует три важных типа сечения:
- круглое;
- прямоугольное;
- эллиптическое.
Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.
Площадь круглого сечения рассчитывается по формуле:
S1 = pi*r2
Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:
S2 = 2*r*h
Сечения конуса
Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:
- круглое;
- эллиптическое;
- параболическое;
- гиперболическое;
- треугольное.
Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.
Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:
S1 = pi*r2*z2/h2
Здесь z – это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z < h, то площадь изучаемого сечения будет всегда меньше ее значения для основания.
Треугольное получается, когда плоскость пересекает фигуру по ее оси вращения. Формой получившегося сечения будет равнобедренный треугольник, сторонами которого являются диаметр основания и две образующие конуса. Как находить площадь сечения треугольного? Ответом на этот вопрос будет следующая формула:
S2 = r*h
Это равенство получается, если применить формулу для площади произвольного треугольника через длину его основания и высоту.
Сечения призмы
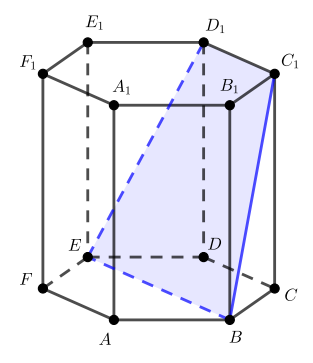
Призма – это большой класс фигур, которые характеризуются наличием двух одинаковых параллельных друг другу многоугольных оснований, соединенных параллелограммами. Любое сечение призмы – это многоугольник. В виду разнообразия рассматриваемых фигур (наклонные, прямые, n-угольные, правильные, вогнутые призмы) велико и разнообразие их сечений. Далее рассмотрим лишь некоторые частные случаи.

Если секущая плоскость параллельна основанию, то площадь сечения призмы будет равна площади этого основания.
Если плоскость проходит через геометрические центры двух оснований, то есть является параллельной боковым ребрам фигуры, тогда в сечении образуется параллелограмм. В случае прямых и правильных призм рассматриваемый вид сечения будет представлять собой прямоугольник.
Пирамида
Пирамида – это еще один многогранник, который состоит из n-угольника и n треугольников. Пример треугольной пирамиды показан ниже.

Если сечение проводится параллельной n-угольному основанию плоскостью, то его форма будет в точности равна форме основания. Площадь такого сечения вычисляется по формуле:
S1 = So*(h-z)2/h2
Где z – расстояние от основания до плоскости сечения, So – площадь основания.
Если секущая плоскость содержит вершину пирамиды и пересекает ее основание, то мы получим треугольное сечение. Для вычисления его площади необходимо обратиться к использованию соответствующей формулы для треугольника.
Как вычислить площадь сечения
При решении задач по геометрии приходится вычислять площади и объемы фигур. Если сделать в любой фигуре сечение, обладая информацией о параметрах самой фигуры, можно найти и площадь этого сечения. Для этого необходимо знать специальные формулы и обладать пространственным мышлением.
Вам понадобится
- Линейка, карандаш, ластик.
Инструкция
Шар является частным случаем простейшей объемной фигуры. Через него можно провести бесконечное количество сечений, и любое из них окажется кругом. Это произойдет независимо от того, насколько близко сечение расположено к центру шара. Вычислить площадь получившегося сечения проще всего в том случае, если оно проведено точно через центр шара, радиус которого известен. В таком случае площадь сечения равна:S=πR^2.
Другой фигурой, площадь сечения которой требуется найти в задачах по геометрии, является параллелепипед. Он имеет ребра и грани. Гранью называется одна из плоскостей параллелепипеда (куба), а ребром – сторона. Параллелепипед, у которого ребра и грани равны, называется кубом. Все сечения куба – квадраты. Зная это свойство, вычислите площадь сечения-квадрата:S=a^2, где a – ребро куба и сторона сечения.
Если в условиях задачи приведен обычный параллелепипед, у которого все грани являются разными, сечение может быть как квадратом, так и прямоугольником с различными сторонами. Сечение, проведенное параллельно двум квадратным граням, является квадратом, а сечение, проведенное параллельно двум прямоугольным – прямоугольником. Если сечение проходит через диагонали параллелепипеда, оно также является прямоугольником.
умножения диагонали нижнего основания на высоту параллелепипеда:S=d*h, где d – диагональ основания, h – высота основания.
Конус – одна из тех фигур вращения, сечения которой могут иметь различную форму. Если рассечь конус параллельно нижнему основанию, сечением будет круг, а если провести сечение параллельно пополам через вершину конуса, получится треугольник. В других случаях сечениями будут трапециевидные фигуры.Если сечением является круг, вычисляйте его площадь по следующей формуле:S=πR^2.Площадь сечения, представляющего собой треугольник, равно произведению половины основания на высоту:S=1/2f*h , где f – основание треугольника, h – высота треугольника.
Источники:
- как найти площадь получившейся фигуры
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Сечения трехмерных фигур — площади и периметр
Умеешь строить сечения трехмерных фигур – точно не пропадешь.
В этой статье я расскажу тебе об алгоритме построения сечений и разберу пример!
Поехали!
Алгоритм определения площади и периметра сечения объемных фигур
- Нарисовать сечение.
- Определить фигуру, которая получилась в этом сечении.
- Вспомнить формулы площади/периметра этой фигуры.
- Найти площадь/периметр фигуры.
Стандартное сечение имеет вид треугольника, круга или четырехугольника. Следовательно, нам необходимо искать площади именно этих фигур.
Площадь сечения
Площадь треугольника
Площадь круга
Площадь прямоугольника
Пример решения задачи
Диаметр основания конуса ( displaystyle left( AB right)) равен ( displaystyle 8) см.
Длина образующей ( displaystyle left( AC; BC right)) равна ( displaystyle 5) см (линия от вершины конуса до любой точки его основания).
Найдите площадь осевого сечения этого конуса.
Осевое сечение конуса – это равнобедренный треугольник ( displaystyle left( ABC right)), высота которого совпадает с высотой конуса ( displaystyle left( CO right)), а основание ( displaystyle left( AB right)) является диаметром основания конуса.
Значит, ( displaystyle S) осевого сечения конуса =( displaystyle S) треугольника ( displaystyle ABC).
Вспомним формулу площади треугольника:
| ( displaystyle S=frac{(COcdot AB)}{2} ) | begin{matrix} AB -длина стороны треугольника \ CO – высота, опущенная на сторону AB \ end{matrix} |
Найдем высоту ( displaystyle Delta ABC):
Рассмотрим ( displaystyle Delta COA).
т.к. ( displaystyle OC) – высота ( displaystyle Delta ABC rightarrow angle COA=90{}^circ rightarrow Delta COA) – прямоугольный.
( displaystyle AO=frac{AB}{2}=frac{8}{2}=4) (т.к. ( displaystyle AO) – радиус окружности, ( displaystyle AB) – диаметр).
Найдем ( displaystyle AC):
По теореме Пифагора:
( displaystyle A{{C}^{2}}=C{{O}^{2}}+A{{O}^{2}}; C{{O}^{2}}=A{{C}^{2}}-A{{O}^{2}}={{5}^{2}}-{{4}^{2}}=9см; CO=sqrt{9}=3см)
Подставим получившиеся значения в формулу площади:
( displaystyle {{S}_{ABC}}=frac{left( COcdot AB right)}{2}=frac{3cdot 8}{2}=)( displaystyle 12см{{ }^{2}})
Площадь осевого сечения этого конуса равна ( displaystyle 12см{{ }^{2}}).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Тема 13.
Задачи по стереометрии
13
.
12
Нахождение площади сечения
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
задачи по стереометрии
Решаем задачи
Показать ответ и решение
Ответ:
б)
Показать ответ и решение
Ответ:
Показать ответ и решение
а) Обозначим через плоскость сечения. Плоскости
и
параллельны, следовательно, плоскость сечет их по параллельным прямым.
Плоскость пересекает
по прямой
Докажем, что прямая
параллельна из этого будет следовать, что она лежит в
так как
.
Прямые в силу правильности шестиугольника
так как в
нем
следовательно, сумма односторонних углов
равна Прямые
следовательно,
Тогда
лежит в
и
— искомое сечение. Кроме того, в четырехугольнике
противолежащие стороны и
параллельны и не равны, следовательно,
— трапеция.
б) Способ 1.
В правильном шестиугольнике также по условию
По теореме Пифагора для треугольника
Найдем полупериметр трапеции:
Равнобокую трапецию можно вписать в окружность, тогда по формуле
Брахмагупты ее площадь равна
Способ 2.
Введём векторный базис из векторов
Длины
этих векторов Из определения правильной призмы
и а поскольку шестиугольник
— правильный, то
прямые и
образуют угол
Тогда можно посчитать скалярное
произведение:
В пункте а) было ранее доказано, что — трапеция. По свойствам
правильного шестиугольника диагональ Тогда для определения
площади сечения можно сначала посчитать площадь треугольника после
чего домножить её на поскольку площадь
составляет половину от
площади Выразим векторы
и
через базисные вектора и найдём
квадраты длин:
Таким образом,
Тогда площадь трапеции равна
Ответ:
б)
Критерии оценки
|
Содержание критерия |
Балл |
|
Имеется верное доказательство |
3 |
|
Обоснованно получен верный ответ в |
2 |
|
ИЛИ |
|
|
имеется верное |
|
|
Имеется верное доказательство |
1 |
|
ИЛИ |
|
|
при обоснованном решении пункта |
|
|
ИЛИ |
|
|
обоснованно получен верный ответ в |
|
|
Решение не соответствует ни одному |
0 |
|
Максимальный балл |
3 |
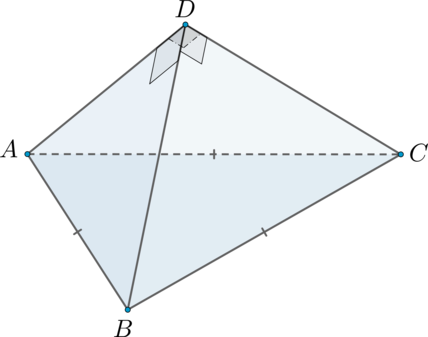
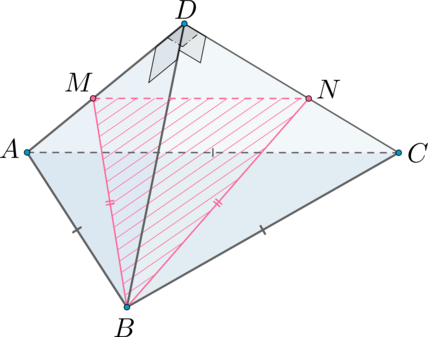
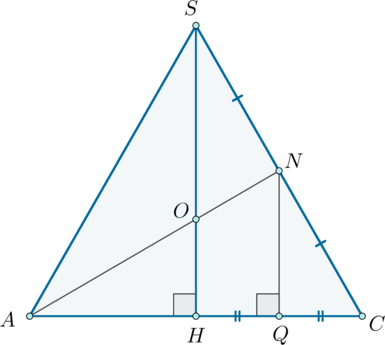
Правильная треугольная пирамида рассечена плоскостью, перпендикулярной основанию и делящей две стороны
основания пополам. Найдите площадь сечения пирамиды этой плоскостью, если известно, что сторона основания равна
, а высота пирамиды равна
.
Показать ответ и решение
Ответ:
Показать ответ и решение
1) Пусть . Две плоскости параллельны, если две пересекающиеся прямые одной
плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Заметим, что т.к. .
Проведем в плоскости прямую
. Т.к.
– середина
, то по теореме Фалеса
– середина . Через точку
в плоскости
проведем
(следовательно,
–
середина ). Таким образом, плоскость, проходящая через прямые
и
, и будет искомой
плоскостью.
Необходимо найти сечение пирамиды этой плоскостью. Соединив точки и
, получим прямую
.
Т.к. ,то
пересечет плоскость
по прямой
(если
, то
, что невозможно ввиду их параллельности).
Таким образом, – искомое сечение, причем
это трапеция.
2) Т.к. все точки – середины отрезков
соответственно,
то:
а)
б)
в)
Заметим, что по теореме о трех перпендикулярах . Таким образом,
– прямоугольная трапеция.
Ответ:
1) Рисунок.
2)
Показать ответ и решение
б) По теореме Менелая для и прямой
имеем:
По условию . Т.к.
и
. Следовательно,
, тогда
. Следовательно,
. Заметим, что
по
углу и двум прилежащим сторонам, следовательно, . Также заметим, что так как
, то
. Также и
. Следовательно,
– равнобедренная
трапеция.
Основания ,
, по теореме Пифагора
. Следовательно,
если провести высоту , то
. Тогда по теореме Пифагора
. Следовательно,
Ответ:
б)
Показать ответ и решение
а) Для того, чтобы доказать, что пирамида является правильной, нужно доказать, что в основании
пирамиды находится правильный многоугольник, а боковые ребра равны.
Возьмем за основание – он правильный по условию.
Осталось доказать, что .
Рассмотрим и
. Они прямоугольные и равны по катету и гипотенузе. Следовательно,
. Аналогично рассматривая другие боковые грани, доказываем, что
.
Следовательно, , чтд.
б) Заметим, что так как и боковые грани – равные треугольники, то
.
Так как , то по теореме Фалеса
, также
.
Из подобия следует:
Найдем .
Так как прямоугольный и равнобедренный, то
, следовательно,
.
Рассмотрим прямоугольный . Так как
, то
.
Рассмотрим теперь :
Так как он равнобедренный, то высота , проведенная к основанию, будет также и медианой.
Следовательно,
Таким образом,
Ответ:
б)
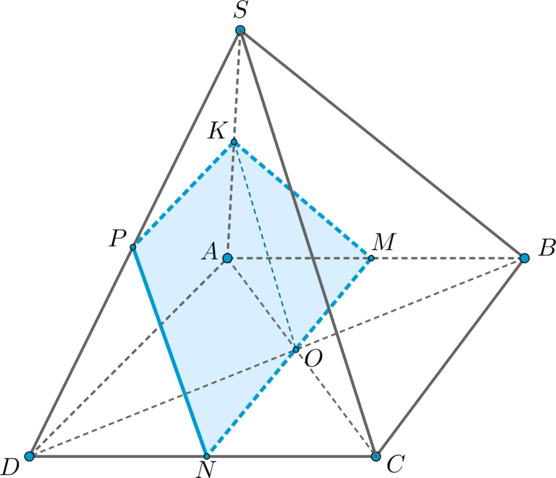
Дана правильная четырехугольная пирамида с вершиной
, стороны основания которой
равны , а боковые ребра равны
.
а) Постройте сечение пирамиды плоскостью, проходящей через точку и середину ребра
параллельно прямой .
б) Найдите площадь построенного сечения.
Показать ответ и решение
б) Заметим, что по теореме о трех перпендикулярах (так как )
. Так как
, то
, следовательно,
. Следовательно, у
четырехугольника диагонали взаимно перпендикулярны. Значит, его площадь можно найти
как
Заметим сразу, что .
Рассмотрим плоскость .
По теореме Менелая:
(это
нам понадобится позже для поиска )
Проведем . Тогда из подобия
и
:
–
середина , следовательно,
. Тогда по теореме Пифагора
Рассмотрим . Так как
, то
Следовательно, площадь сечения равна
Показать ответ и решение
1) Пусть – середина
,
– медианы грани
,
– медианы грани
,
.
– высота пирамиды.
Найдем сечение пирамиды плоскостью .
Т.к. пирамида правильная, то – равнобедренный,
.
Таким образом, плоскость содержит прямую
, параллельную
, следовательно,
плоскость пересечет плоскость
по прямой, параллельной
(если это не так, то линия
пересечения этих плоскостей и
не может быть
параллельна ).
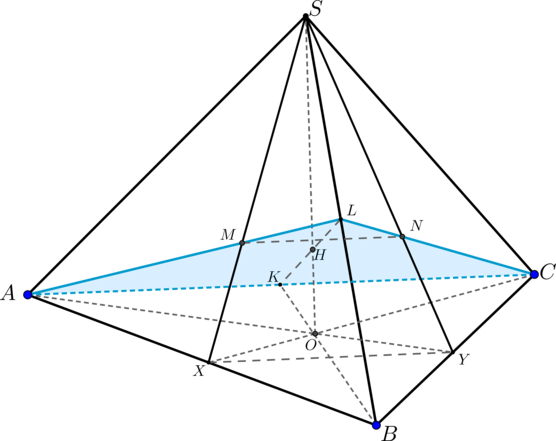
Прямая, проходящая через точку и параллельная
(или
) – это
. Следовательно,
сечением является равнобедренный треугольник .
2) Пусть . Тогда по теореме о трех перпендикулярах
как наклонная
( как проекция). Следовательно, и
.
Тогда .

Рассмотрим .
Тогда по теореме косинусов для :
Значит, .
Ответ:
.
Показать ответ и решение
а) 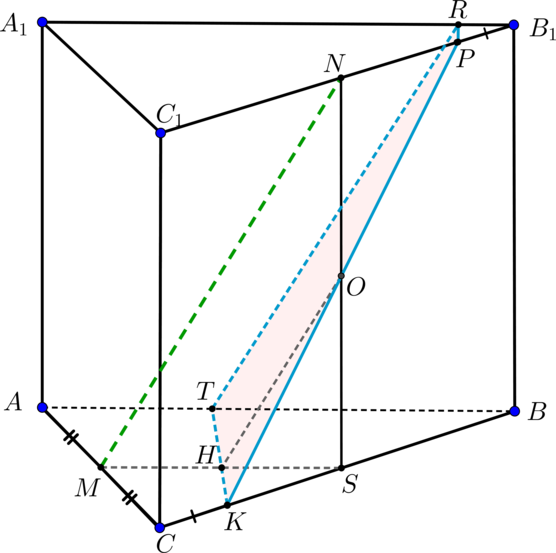
Если прямая параллельна некоторой прямой, лежащей в
. Проведем
. В плоскости
проведем
. Тогда прямая
. Так как плоскости
и
параллельны, то
пересечет плоскость
по прямой, параллельной . Следовательно, проведем
. Таким образом,
– искомое
сечение (трапеция).
б) Заметим, что . Т.к.
– средняя линия треугольника
. Так как
, то по теореме косинусов
. Таким образом, по обратной теореме Пифагора треугольник
–
прямоугольный, следовательно, . Таким образом, по теореме о трех перпендикулярах, из
того, что .
Найдем основания трапеции и
.
.
.
Таким образом,
Ответ:
б)
Показать ответ и решение
а) 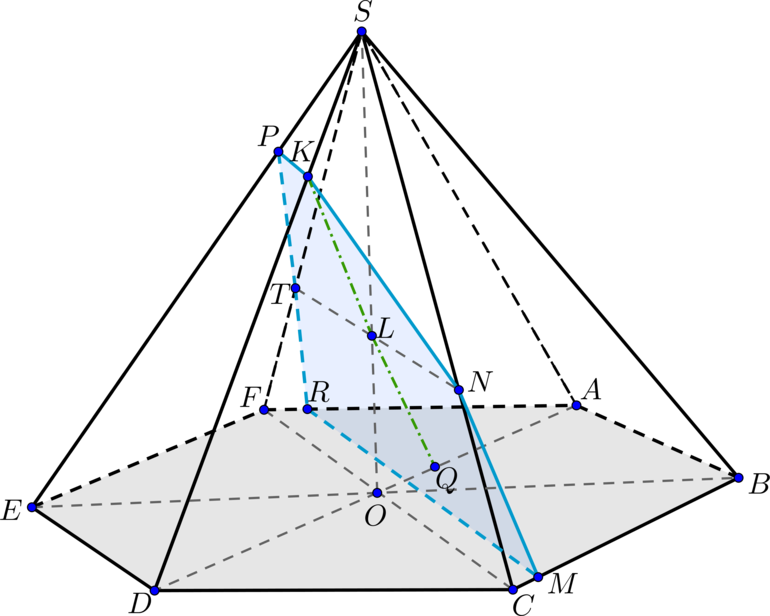
Две плоскости параллельны, если две пересекающиеся прямые из одной плоскости будут
параллельны некоторых двум пересекающимся прямым из другой плоскости.Проведем через точку
прямые, параллельные и
.
Из свойства правильного шестиугольника следует, что . Проведем в плоскости
через
точку :
.
Тогда по теореме Фалеса
В плоскости проведем через точку
:
.
Из теоремы Фалеса следует, что
Пусть . Из свойств правильного шестиугольника следует, что
.
Тогда по теореме Фалеса
б) Достроим сечение пирамиды плоскостью . Плоскость
пересечет плоскость основания по
прямой . Значит,
Найдем все их стороны.
Из подобия
Из подобия
Достроим трапецию до треугольника
– он правильный.
Из подобия
Найдем из грани
:
По теореме косинусов .
В :
по теореме косинусов
Обозначим высоту трапеции за
. Тогда
Высота трапеции
Тогда площадь сечения
Ответ:
б)
You may encounter situations in which you have a three-dimensional solid shape and need to figure out the area of an imaginary plane inserted through the shape and having borders defined by the boundaries of the solid.
For example, if you had a cylindrical pipe running under your home measuring 20 meters (m) in length and 0.15 m across, you might want to know the cross-sectional area of the pipe.
Cross sections can be perpendicular to the orientation of the axes of the solid if any exist. In the case of a sphere, any cutting plane through the sphere regardless of orientation will result in a disk of some size.
The area of the cross-section depends on the shape of the solid determining the cross-section’s boundaries and the angle between the solid’s axis of symmetry (if any) and the plane that creates the cross section.
Cross-Sectional Area of a Rectangular Solid
The volume of any rectangular solid, including a cube, is the area of its base (length times width) multiplied by its height: V = l × w × h.
Therefore, if a cross section is parallel to the top or bottom of the solid, the area of the cross-section is l × w. If the cutting plane is parallel to one of the two sets the sides, the cross-sectional area is instead given by l × h or w × h.
If the cross-section is not perpendicular to any axis of symmetry, the shape created may be a triangle (if placed through a corner of the solid) or even a hexagon.
Example: Calculate the cross-sectional area of a plane perpendicular to the base of a cube with a volume of 27 m3.
-
Since l = w = h for a cube, any one edge of the cube must be 3 m long (since 3
× 3
× 3 = 27). A cross-section of the type described would therefore be a square 3 m on a side, giving an area of 9 m2.
Cross-Sectional Area of a Cylinder
A cylinder is a solid created by extending a circle through space perpendicular to its diameter. The area of a circle is given by the formula πr2, where r is the radius. It therefore makes sense that the volume of a cylinder would be the area of one of the circles forming its base.
If the cross-section is parallel to the axis of symmetry, then the area of the cross-section is simply a circle with an area of πr2. If the cutting plane is inserted at a different angle, the shape generated is an ellipse. The area uses the corresponding formula: πab (where a is the longest distance from the center of the ellipse to the edge, and b is the shortest).
Example: What is the cross-sectional area of the pipe under your home described in the introduction?
-
This is just πr2 = π(0.15 m)2=
π(0.0225) m2 = 0.071 m2. Note that the length of the pipe is irrelevant to this calculation.
Cross-Sectional Area of a Sphere
Any theoretical plane placed through a sphere will result in a circle (think about this for a few moments). If you know either the diameter or the circumference of the circle the cross-section forms, you can use the relationships C = 2πr and A = πr2 to obtain a solution.
Example: A plane is rudely inserted through the Earth very close to the North Pole, removing a section of the planet 10 m around. What is the cross-sectional area of this chilly slice of Earth?
- Since C = 2πr = 10 m, r = 10/2π = 1.59 m; A = πr2= π(1.59)2= 7.96 m2.