Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Площадь четырехугольника по диагоналям и углу между ними
Площадь четырехугольника через стороны и углы между этими сторонами
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади четырехугольника
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула | |
| 1 | диагональ и угол между ними | |
|
| 2 | стороны и углы между этими сторонами | |
|
| 3 | стороны (по Формуле Брахмагупты) |
|
|
| 4 | стороны и радиус вписанной окружности | |
|
| 5 | стороны и углы между ними | |
Площадь частных случаев четырехугольников
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь четырехугольника – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
Калькулятор расчета площади четырехугольника
В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
1. Через диагонали и угол между ними
Формула расчета
2. По всем сторонам (формула Брахмагупты)
Примечание: Если вокруг четырехугольника можно описать окружность.
Формула расчета
p – полупериметр четырехугольника, равняется:
Площади четырехугольников
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
a и b – смежные стороны
d – диагональ,
φ – любой из четырёх углов между диагоналями
Получается из верхней формулы подстановкой d=2R
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
a – сторона,
ha – высота, опущенная на эту сторону
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
a – сторона,
ha – высота, опущенная на эту сторону
a – сторона,
φ – любой из четырёх углов ромба
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
a и b – основания,
c и d – боковые стороны
a и b – неравные стороны,
φ – угол между ними
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними
,
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,
Формулу называют «Формула Брахмагупты»
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник |  |
S = ab | |
 |
|||
 |
|||
| Параллелограмм |  |
||
 |
|||
 |
|||
| Квадрат |  |
S = a 2 | |
 |
S = 4r 2 | ||
 |
|||
 |
|||
| Ромб |  |
||
 |
|||
 |
|||
 |
|||
 |
|||
| Трапеция |  |
||
 |
S = m h | ||
 |
|||
 |
|||
| Дельтоид |  |
S = ab sin φ | |
 |
 |
||
 |
|||
 |
|||
| Произвольный выпуклый четырёхугольник |  |
||
| Вписанный четырёхугольник |  |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними
,
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
| Прямоугольник | |
|
|
|
|
|
|
| Параллелограмм | |
|
|
|
|
|
|
| Квадрат | |
|
S = a 2
где |
|
S = 4r 2 |
|
|
|
|
| Ромб | |
|
|
|
|
|
|
|
|
|
|
| Трапеция | |
|
|
|
|
|
|
|
|
| Дельтоид | |
|
|
|
где |
|
|
|
|
| Произвольный выпуклый четырёхугольник | |
|
|
| Вписанный четырёхугольник | |
|
| Прямоугольник |
|
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
Параллелограмм
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Квадрат
где
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
Ромб
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
Трапеция
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны ,
Дельтоид
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
где
a и b – неравные стороны,
r – радиус вписанной окружности
Произвольный выпуклый четырёхугольник
φ – любой из четырёх углов между ними
Вписанный четырёхугольник
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле
,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле
,
где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
,
что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
[spoiler title=”источники:”]
http://www.resolventa.ru/spr/planimetry/sqf.htm
[/spoiler]
На этой странице представлена справочная информация с формулами для вычисления площадей простых фигур (сечений) с указанием положения их центров тяжестей.
Эта страничка будет полезна при расчёте более сложных фигур (составных поперечных сечений): определении положения центра тяжести, а также общей площади.
Центры тяжести
Для всех фигур, положение центра тяжести в статье обозначается буквой – C, это наиболее используемый вариант. Также иногда центр тяжести обозначают буквой – O.
Формулы для расчёта площадей
В сопромате площадь поперечного сечения обозначается буквой – A, однако, в некоторой литературе ты можешь встретить обозначения с буквой – F.
Другую справочную информацию, размещённую на сайте – ssopromat.ru, можешь найти, перейдя по указанной ссылке.
Привет всем!
Эту задачу решали выпускники 2013 года на реальном ЕГЭ. Она, как водится, похожа на задачу для Урала. Звучит она так:
В правильной четырехугольной пирамиде `MABCD` с вершиной `M` стороны основания равны 6, а боковые ребра равны 12. Найдите площадь сечения пирамиды плоскостью, проходящей через точку `C` и середину ребра `MA` параллельно прямой `BD`.
Чтобы вникнуть в задачу, построим пирамиду. А затем поймем, как пройдет сечение.
Наша пирамида выглядит так:
Чтобы построить сечение, обозначим середину ребра `MA` как `N`. Дальнейшие шаги:
- Соединим точки `N` и `C`. Отрезок `NC` пересечет высоту пирамиды `MH` в точке `E`.
- В плоскости `MBD` через точку `E` проведем прямую, параллельную `BD`. Она пересечет ребра `MB` и `MD` в точках `P` и `Q` соответственно.
- Четырехугольника `NPCQ` — искомое сечение.
Заметим, что диагонали искомого четырехугольника перпендикулярны (доказать самостоятельно). Вынесем его на отдельный рисунок.
Поскольку диагонали перпендикулярны, то площадь `NPCQ` равна половине произведения диагоналей. Следующий шаг — найти их длины. Начнем с длины `NC`.
Рассмотрим `triangle AMC`.
Нам известны боковые стороны и длина отрезка `NM` (она равна половине `MA` по условию). Чтобы найти `NC`, достаточно знать `angle M`, тогда мы легко найдем нужный отрезок по теореме косинусов. Однако `angle M` тоже можно легко найти по теореме косинусов.
$$cos angle M = frac {AC^2 – AM^2 – CM^2}{-2cdot AM cdot CM} = frac{36cdot 2 – 144 -144}{-2cdot 144} = frac{216}{288}=frac{3}{4}.$$
Теперь из `triangle MNC` найдем длину `NC`.
$$NC^2 = MN^2 + MC^2 -2cdot MN cdot MC cdot cos angle M = 36 + 144 – 2 cdot 72 cdot frac{3}{4} = 180 – 108 = 72,$$
$$NC = 6sqrt{2}.$$
Длина `NC` теперь известна. Для дальнейшего решения осталось заметить, что `NC` и `MH` — медианы в равнобедренном треугольнике, значит они делятся в отношении `2:1`, считая от вершины, т. е. `ME : EH = 2 : 1`.
Из `triangle BDM` найдем `PQ`.
Длину `BD` мы найдем как диагональ квадрата, лежащего в основании. `HD` равно половине `BD`. Поскольку `PQ parallel BD`, то `triangle MEQ sim triangle MHD` с коэффициентом подобия `2 : 3` (коэффициент подобия можно получить, если вспомнить про соотношение длин отрезков `ME` и `EH`, оно отмечено на рисунке).
Отсюда получаем, что `EQ = 2sqrt{2}`, a `PQ = 4 sqrt{2}`.
Таким образом, теперь нам известны обе диагонали четырехугольника – сечения.
Вычислим его площадь.
$$S_{NPCQ} = PQ cdot NC cdot frac{1}{2}= 4sqrt{2} cdot 6sqrt{2} cdot frac{1}{2} = 24.$$
Ответ
24
Спасибо всем, кто внимательно прочитал это решение и разобрался в нем. Оставляйте комментарии и лайки, они очень помогут мне и этому сайту.
Поперечным сечением называется фигура, образованная пересечением продолговатого тела с воображаемой плоскостью, расположенных перпендикулярно друг другу, т.е. когда тело рассекается строго поперек его длины.
Площадь и размеры (длина и ширина) поперечного сечения равны соответствующим размерам этой фигуры.
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.
Математика ЕГЭ
Информатика ЕГЭ
Алексей Шевчук
- ведущий курсов и автор учебника ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — 18 лет;
- в 2021 году сдал ЕГЭ — 100 баллов (мат, физ) и 98 баллов (инф);
- рейтинг на Профи.ру — «4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Площадь поперечного сечения
В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.
Формулы для расчета площади основных фигур.
Пример: Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением. Для расчета общей площади, сложное сечение раскладывается на простые фигуры:
Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто. В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:
A=A1+A2+A3-A4
Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м2, см2 или мм2.
Площадь составного сечения
Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым. Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.
Эти сечения сами по себе тоже являются сложными. Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.
В результате сложив все составляющие профили, получим площадь всего сечения.
Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.
Сечение проводов в домах старой застройки и предельная нагрузка
В многоэтажках советского периода используется алюминиевая проводка. С учетом правильного соединения узлов в распредкоробе, качества изоляции и надежности контактов соединения она прослужит от 10 до 30 лет.
При необходимости подключения техники с большой энергоемкостью в домах с проводкой из алюминия на основе мощности потребления подбирается сечение и диаметр жил. Все данные указаны в таблице.
| Ток, А | Максимальная мощность, ВА | Диаметр кабеля, мм | Сечение кабеля, мм2 |
| 14 | 3000 | 1,6 | 2 |
| 16 | 3500 | 1,8 | 2,5 |
| 18 | 4000 | 2 | 3 |
| 21 | 4600 | 2,3 | 4 |
| 24 | 5300 | 2,5 | 5 |
| 26 | 5700 | 2,7 | 6 |
| 31 | 6800 | 3,2 | 8 |
| 38 | 8400 | 3,6 | 10 |
Информация о прямоугольнике
Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.
Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.
Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.
Свойства и признаки
Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:
- Условие параллельности и равенства противоположных сторон.
- Наличие четырех прямых углов.
- Равенство диагоналей.
- Квадрат диагонали равен суммарному значению квадратов двух сторон, которые не противоположны.
- Все стороны не равны между собой.
Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают. Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:
- Углы равны между собой 90 градусов.
- Противолежащие параллельные стороны равны.
- Сумма всех внутренних углов составляет 360.
- Диагональ, проведенная внутри прямоугольника, делит его на два равнозначных треугольника, которые являются равновеликими. Они равны по третьему признаку равенства треугольников (размерности сторон одной фигуры равны значениям сторон другой фигуры).
- Треугольники, полученные при проведении двух диагоналей, равны по всем признакам (углам и сторонам).
- Диагонали пересекаются между собой в точке, которая делит их на четыре равные части.
- Точка пересечения диагоналей — центр симметрии.
- Сумма квадратов двух диагоналей соответствует суммарному значению квадратов всех сторон фигуры.
Однако свойств и признаков фигуры недостаточно для решения задач. Следует знать основные соотношения и формулы.
Периметр и размерность
Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + [2 * (2d 2 — 2a 2 )]^(1/2) и P = 2b + [2 * (2d 2 — 2b 2 )]^(1/2).
Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.
Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * ^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.
Формула площади треугольника по двум сторонам и углу между ними
S = 1 2 ⋅ b ⋅ c ⋅ sin ( α ) S=frac{1}{2}cdot bcdot ccdotsin(alpha) S=21⋅b⋅c⋅sin(α),
b , c b, c b,c — стороны треугольника;
α alpha α — угол между сторонами b b b и c c c.
Пример
Стороны треугольника равны 5 (см.) и 6 (см.), угол между ними равен 30 градусов. Найти площадь треугольника.
Решение
b = 5 b=5 b=5 c = 6 c=6 c=6 α = 3 0 ∘ alpha=30^{circ} α=30∘
S = 1 2 ⋅ 5 ⋅ 6 ⋅ sin ( 3 0 ∘ ) = 7.5 S=frac{1}{2}cdot 5cdot 6cdotsin(30^{circ})=7.5 S=21⋅5⋅6⋅sin(30∘)=7.5 (см. кв.)
Ответ: 7.5 (см. кв.)
Контрольная по геометрии недорого на сервисе Студворк от профильных экспертов!
Приступаем к расчёту
Так как задача – найти истинную площадь, то из полученного значения необходимо вычесть величину толщины стенки. Следовательно, формула приобретает вид:
- S = π (D/2 – N) 2 ;
- В этой записи D – внешний диаметр окружности;
- N – толщина стенки трубы.
Чтобы вычисления были максимально точными, следует вписать больше знаков после запятой в числе π (пи).
D = 1 м.; N = 0,01 м.
Для упрощения возьмём π = 3,14. Подставляем значения в формулу:
S = π (D/2 – N) 2 = 3,14 (1/2 – 0,01) 2 = 0,754 м 2 .
Некоторые физические особенности
От площади сечения трубы зависит скорость движения жидкостей и газов, которые по ней транспортируются. Надо выбрать оптимальный диаметр. Не менее важным является и внутреннее давление. Именно от его величины зависит целесообразность выбора сечения.
При расчёте учитывается не только давление, но и температура среды, её характер и свойства. Знание формул не освобождает от необходимости изучения теории. Расчёт труб канализации, водоснабжения, газоснабжения и отопления опирается на информацию справочников. Важно, чтобы выполнялись все необходимые условия при выборе сечения. Его величина также зависит и от характеристик используемого материала.
О чём стоит помнить?
Площадь сечения трубы – один из важных параметров, который следует учитывать при расчёте системы. Но наравне с тем высчитываются параметры прочности, определяется, какой материал выбрать, изучаются свойства системы в целом и пр.
Произвести расчет сечения трубы довольно просто, ведь для этого есть ряд стандартных формул, а также многочисленные калькуляторы и сервисы в интернете, которые могут выполнить ряд простых действий. В данном материале мы расскажем о том, как рассчитать площадь сечения трубы самостоятельно, ведь в некоторых случаях нужно учитывать ряд конструкционных особенностей трубопровода.
Вычисление сечения провода для линии розеток
- материал провода и способ укладки – трехжильный ВВГнг-кабель из меди, спрятанный в стене;
- особенности сечения – оптимальная величина составляет 1,5 мм2, т.е. понадобится кабель 3х1,5;
- использование розетки. Если подключается только машинка-автомат, характеристик будет достаточно;
- система защиты – автомат, номинальный ток которого 10 А.
Для двойных розеток применяется кабель из меди с сечением 2,5 мм2 и автомат номиналом 16 А.
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
, где — сторона.
Площадь равностороннего треугольника через высоту
, где — высота.
Формулы вычислений
При проведении вычислений нужно учитывать, что по существу трубы имеют форму цилиндра. Поэтому для нахождения площади их сечения можно воспользоваться геометрической формулой площади окружности. Зная внешний диаметр трубы и значение толщины его стенок, можно найти показатель внутреннего диаметра, который понадобится для вычислений.
Стандартная формула площади окружности такова:
S=π×R2, где
π – постоянное число, равное 3,14;
R – величина радиуса;
S – площадь сечения трубы, вычисленная для внутреннего диаметра.
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм2);
- квадратный сантиметр (см2);
- квадратный дециметр (дм2);
- квадратный метр (м2);
- квадратный километр (км2);
- гектар (га).
Как найти площадь поперечного сечения прямоугольника?
Как найти площадь поперечного сечения прямоугольника?
Площадь сечения профилированной трубы считается по формуле площади прямоугольника: S = a * b, где a и b — длины сторон прямоугольника.
Как считать площадь поперечного сечения?
Площадь сечения круга или шара можно найти по формуле:
- S = πR2 …
- c = S*q*r*t*(a2 + b2) …
- S= c*h. …
- S=a*b. …
- S =2R*h. …
- S =2а*h.
Как найти площадь поперечного сечения стержня?
S = π * d 2 / 4, где На этой странице представлен самый простой онлайн калькулятор расчета площади поперечного сечения стержня, если известен диаметр стержня.
Как найти длину трубы зная диаметр?
Внутренний и наружный диаметр, толщина стенки, радиус Имея эти два значения, легко высчитать внутренний диаметр — от наружного отнять удвоенную толщину стенки: d = D — 2*S. Если у вас наружный диаметр 32 мм, толщина стенки 3 мм, то внутренний диаметр будет: 32 мм — 2 * 3 мм = 26 мм.
Как рассчитать объем трубы зная диаметр и длину?
Для расчета необходимо знать данные диаметра трубы. Его обозначают буквой D и рассчитывают по формуле R x 2. Определяется также длина окружности….Сама формула расчета, имеет следующий вид:
- V = S x L.
- Объем трубы – V;
- Площадь сечения – S;
- Длина – L.
Как рассчитать длину трубы по весу?
Расчет ведется по формуле m = ro / 7850 * 0.
Сколько весит 1 метр трубы?
Вес и сортамент стальных магистральных труб по ГОСТ’у /div>
| Наружный диаметр трубы, мм | Толщина стенки, мм | Масса 1 метра погонного, кг |
|---|---|---|
| 377 | 8,5 | 77,25 |
| 9 | 81,68 | |
| 426 | 5 | 51,9 |
| 5,5 | 57,04 |
Сколько весит метр трубы таблица?
Вес трубы стальной
| диаметр трубы, мм | Стенка, мм | Масса 1 метра, кг |
|---|---|---|
| Ø30 | 1,0 мм. |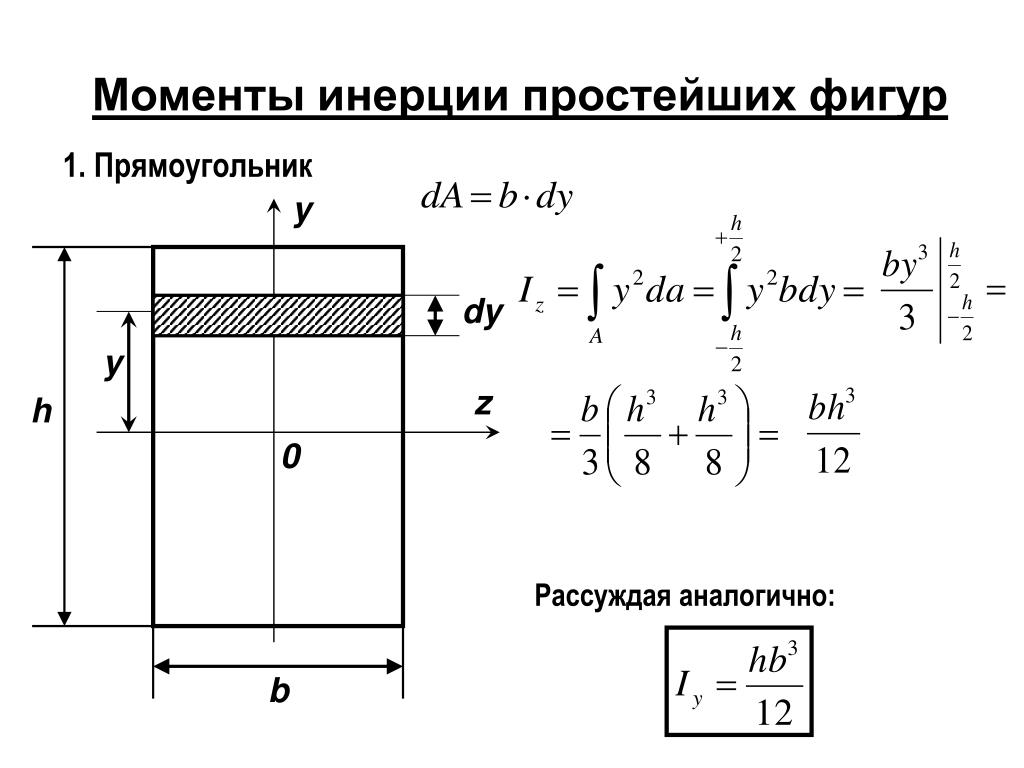
0,715кг |
| Ø30 | 1,2мм | 0,852кг |
| Ø30 | 1,4мм | 0,987кг |
| Ø30 | (1,5)мм | 1,165кг |
Сколько весит метр трубы 57х3?
Теоретический вес труб стальных круглых
| Наружный диаметр, мм | Толщина стенки, мм | Теоретический расчёт Массы 1м, кг |
|---|---|---|
| Труба 57 | 2,0 | 57х2 вес метра 2,713 |
| Труба 57 | 2,5 | 57х2,5 вес метра 3,360 |
| Труба 57 | 3,0 | 57 х3 вес метра 3,995 |
| Труба 57 | 3,5 | 57х3,5 вес метра 4,618 |
Сколько весит 1 метр трубы диаметром 57 мм?
Вес метра трубы 57 с толщиной стенки 1.
Сколько стоит метр 57 трубы?
Труба электросварная 57 мм — от 100 руб/м купить в Сталь-Эксперт (цена)
Сколько метров в тонне трубы 57?
Теоретический вес горячедеформированных (г/д) бесшовных труб (ГОСТ 8732-78 и ГОСТ 8731-74)
| Наружный диаметр, мм | Толщина стенки, мм | Метров в тонне |
|---|---|---|
| 108 | 5 | 78,7 |
| 5,5 | 71,9 | |
| 6 | 66,3 | |
| 7 | 57,4 |
Сколько метров в тонне трубы?
| Наружный диаметр, мм | Толщина стенки, мм | Ориентировочное количество метров в тонне |
|---|---|---|
| 12 | 1,0 | 3690,04 |
| 1,2 | 3125,00 | |
| 1,4 | 2732,24 | |
| 1,5* | 2577,32 |
Сколько метров профильной трубы в тонне?
Теоретический удельный вес квадратных профильных труб (ГОСТ 8639-82)
| Размеры профильной трубы, мм | Толщина стенки профильной трубы, S, мм | Метров в тонне |
|---|---|---|
| 25 | 1 | 1351,4 |
| 1,5 | 934,6 | |
| 2 | 719,4 | |
| 2,5 | 595,2 |
Как найти 1 погонный метр трубы?
Как посчитать погонный метр? Вам нужно точное значение плотности материала, из которого сделано изделие.
Умножьте плотность на объем, чтобы получить значение массы погонного метра. Умножьте массу погонного метра на длину трубопровода.
Сколько будет 1 погонный метр?
Это очень упрощает учет. Погонный метр равен одному метру. Это единица измерения длины, без учёта ширины, или толщины. Можно взять в руки рулетку измерить длину в один метр, это и будет тот самый погонный метр.
Как рассчитать цену за погонный метр трубы?
Стоимость 1 погонного метра металлопроката можно определить по универсальной формуле: Цпм = Sпр х ρст х Цт / 1000, где
Как рассчитать цену погонного метра?
При необходимости можно перевести полученную площадь в погонные метры. Формула перевода такова – Pm = S/a, где a – это ширина линолеума. Например, имеется комната шириной 3 м и длиной 7 м.
Как рассчитать цену за квадратный метр?
Для расчета средней стоимости квадратного метра по абсолютному значению нам достаточно суммировать цены, суммировать метры и разделить суммированную цену на суммированную площадь.
Рассчитаем стоимость квадратного метра для каждой квартиры и сопоставим результаты со средним значением.
Как считается погонный метр?
Погонный метр — это и есть метр, равный 100 см в длину. … Погонный метр — это величина, единица измерения длины или расстояния чего либо в метрах. Погонный метр = метр. В погонных метрах считают определенные отрезки поверхностей, для уточнения, измерения длинны, расстояния.
Расчет прямоугольного сечения балки по условию прочности
Пример решения задачи по подбору минимальных размеров балки прямоугольного поперечного сечения, обеспечивающих её необходимую прочность.
Задача
Для заданной стальной балки подобрать размеры прямоугольного поперечного сечения по условию прочности.
Соотношение сторон сечения h=2b (h – высота, b – ширина).
Полученные размеры принять согласно ГОСТ 6636.
Допустимые напряжения для материала балки [σ]=160МПа.
Другие примеры решений >
Помощь с решением задач >
Решение
Предыдущие пункты решения задачи:
- Определение опорных реакций
- Построение эпюр внутренних поперечных сил и изгибающих моментов
- Расчет момента сопротивления сечения балки по условию прочности
Минимально необходимый расчетный момент сопротивления сечения балки составил
В случаях, когда система изгибающих нагрузок действующих на балку расположена в вертикальной плоскости сечение тоже следует располагать вертикально.
По справочнику находим формулу осевого момента сопротивления прямоугольного сечения
Используя заданное соотношение сторон (h=2b), уменьшим количество переменных в выражении
и запишем необходимое неравенство
откуда находим расчетную высоту прямоугольного сечения
Из заданного соотношения сторон определяем расчетную ширину сечения
Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки.
При отсутствии дополнительных условий расчетные размеры можно округлить до целого значения в миллиметрах исключительно в большую сторону (h=153мм, b=77мм).
По ГОСТ 6636 нормальных линейных размеров выбираются ближайшие значения в сторону увеличения.
Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=155мм, b=80мм.
После принятия размеров согласно ГОСТ заданное соотношение сторон может несколько измениться. Это нормально.
Оценка экономичности сечений >
Построение эпюры нормальных напряжений >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Помощь с решением
ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ
- Техническая механика (техмех)
- Теоретическая механика (теормех)
- Сопротивление материалов (сопромат)
- Строительная механика (строймех)
- Теория механизмов и машин (ТММ)
- Детали машин и ОК (ДМ)
Поиск формул и решений задач
Свойства прямоугольного сечения | Calcresource
Соглашение
-Геометрия
-Момент инерции
-Момент инерции и изгиба
-Полярный момент инерции
-Эластичный модуль
-Эластичные напряжения
-пластиковый модул
-около
-эластичные напряжения
-пластик
-около
-Эластичные напряжения
-пластик
-около
-Эластичные напряжения
-пластик
-около ось x
— Вокруг оси y
— Радиус вращения
— Формулы прямоугольного сечения
— Связанные страницы
93}{12}
Момент инерции и изгиб
Момент инерции (секундный момент или площадь) используется в теории балок для описания жесткости балки при изгибе.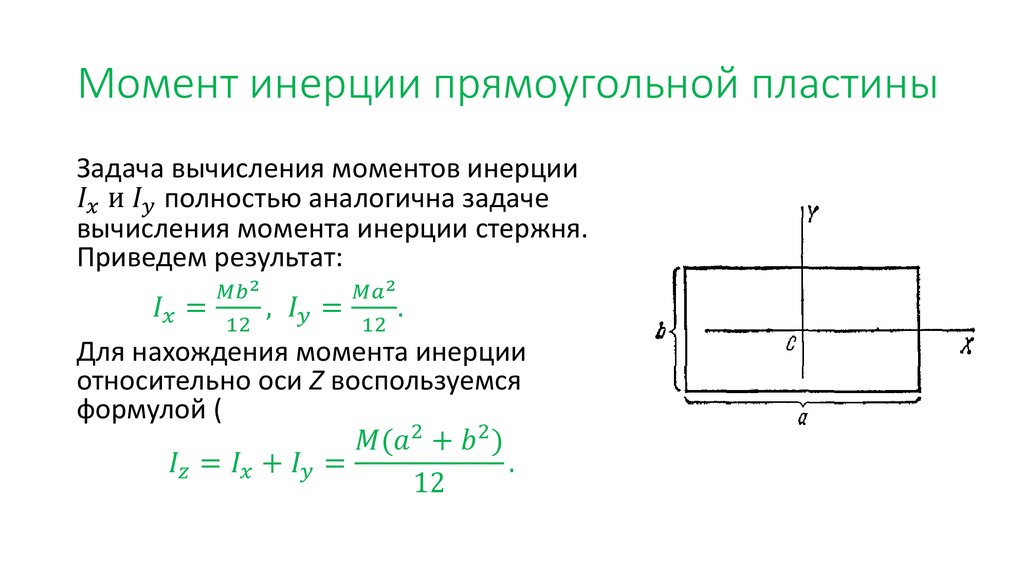
Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:
M = Etimes I times kappa
где E — модуль Юнга, свойство материала , а kappa — кривизна балки из-за приложенной нагрузки. Следовательно, из предыдущего уравнения видно, что когда к поперечному сечению балки приложен определенный изгибающий момент М, результирующая кривизна обратно пропорциональна моменту инерции I.94 .
Полярный момент инерции
Полярный момент инерции описывает жесткость поперечного сечения по отношению к крутящим моментам, так же как описанные выше плоские моменты инерции связаны с изгибом. Расчет полярного момента инерции I_z вокруг оси z (которая перпендикулярна плоскости сечения) можно выполнить с помощью теоремы о перпендикулярных осях:
I_z = I_x + I_y
, где I_x и I_y — моменты инерция вокруг осей x и y, которые взаимно перпендикулярны оси z и сходятся в одном начале координат.
Модуль упругости
Модуль упругости S_x любого поперечного сечения вокруг оси x (в центре) описывает реакцию сечения на упругий изгиб.
Он определяется как:
S_x = frac{I_x}{Y}
, где I_x — момент инерции секции вокруг оси x, а Y — расстояние от центра тяжести волокна секции, параллельное оси x и измеренное перпендикулярно от него. Как правило, представляют интерес более удаленные волокна. Для прямоугольника а наиболее удаленными от оси x волокнами являются волокна на верхнем и нижнем краях b на расстоянии, равном h/2. Таким образом, применение приведенной выше формулы для прямоугольного поперечного сечения приводит к следующему выражению для модуля упругого сечения вокруг оси x: 92}{6}
Можно заметить, что формула для S_y становится идентичной формуле для S_x, если заменить b на h и наоборот.
Упругие напряжения
Если к оси x приложен изгибающий момент M_x, сечение будет реагировать нормальными напряжениями, линейно изменяющимися с расстоянием от нейтральной оси (которая в упругом режиме совпадает с центроидальной осью x-x). Над нейтральной осью напряжения равны нулю. Абсолютный максимум сигма будет иметь место на самом удаленном волокне, величина которого определяется формулой: 93 .
Модуль пластичности
Модуль пластичности аналогичен упругому модулю, но определяется с допущением полной пластической текучести поперечного сечения вследствие изгибного изгиба. В этом случае все сечение разделено на две части, одну на растяжение и одну на сжатие, каждая из которых находится под однородным полем напряжений. Для материалов с равными напряжениями текучести при растяжении и сжатии это приводит к разделению сечения на две равные области, A_t, при растяжении, и A_c, при сжатии, разделенные нейтральной осью. Это результат уравновешивания внутренних сил в поперечном сечении при пластическом изгибе. В самом деле, общая сжимающая сила по всей сжимаемой площади будет равна A_cf_y, если предположить условия пластичности (т. е. материал будет деформироваться везде) и что предел текучести при сжатии равен f_y. Точно так же растягивающая сила будет равна A_t f_y, если использовать те же предположения. Обеспечение равновесия:
A_cf_y = A_t f_yRightarrow
A_c= A_t
Ось называется пластической нейтральной осью , а для несимметричных сечений она не совпадает с упругой нейтральной осью (которая снова является центроидальной).
Однако прямоугольное сечение является симметричным (имеет две оси симметрии), поэтому его пластические нейтральные оси совпадают с упругими. Другими словами, пластические нейтральные оси проходят через центр тяжести прямоугольника.
Вокруг оси x
Модуль пластичности при изгибе вокруг оси x определяется по общей формуле:
Z = A_c Y_c + A_t Y_t
где Y_c, расстояние от центра масс области сжатия до пластика нейтральная ось и Y_t — соответствующее расстояние от центра тяжести области растяжения.
В случае прямоугольного поперечного сечения пластическая нейтральная ось проходит через центр тяжести, разделяя всю площадь на две равные части. Область сжатия будет прямоугольником с размерами b и h/2. Его центроид будет находиться на расстоянии, равном h/4, от оси x, как показано на следующем рисунке. То же самое относится и к области растяжения. Следовательно, модуль пластического сечения прямоугольного сечения при изгибе x-x находится следующим образом: 92}{4}
Еще раз, это последнее уравнение может быть получено из модуля пластичности Z_x, если мы заменим h на b и наоборот.
Радиус вращения
Радиус вращения R_g поперечного сечения относительно оси определяется по формуле:
R_g = sqrt{frac{I}{A}}
где I момент инерции поперечного сечения вокруг той же оси и A его площади. Размеры радиуса вращения [Длина]. Он описывает, насколько далеко от центра тяжести распределена область. Малый радиус указывает на более компактное сечение. Для прямоугольного сечения замена приведенного выше выражения дает следующие радиусы вращения вокруг центральных осей x и y соответственно:
R_{gx} = frac{h}{2sqrt{3}}
R_{gy} = frac{b}{2sqrt{3}}
Круг – это фигура с минимальным радиусом вращения по сравнению с любым другим сечением той же площади A.
Формулы для прямоугольного сечения
В следующей таблице приведены формулы, которые можно использовать для расчета основных механических свойств прямоугольного сечения.
Свойства прямоугольного сечения |
|
|---|---|
| Количество 92}{4} | |
| Радиус вращения |
R_{gx} = frac{h}{2sqrt{3}} R_{gy} = frac{b}{2sqrt {3}} |
Связанные страницы
Понравилась эта страница? Поделись с друзьями!
Площадь прямоугольника с калькулятором.
Определение и формула Площадь прямоугольника с калькулятором. Определение и формула — Открытый справочник по математике
Открытый математический справочник
Главная
Контакт
О
Предметный указатель
Количество квадратных единиц, необходимое для полного заполнения прямоугольника.
Формула: Ширина × Высота
Попробуйте это Перетащите оранжевые точки, чтобы переместить и изменить размер прямоугольника. По размеру прямоугольника
изменяется, площадь пересчитывается.
Формула площади
Площадь прямоугольника находится путем умножения ширины на высоту. Как формула:
где
w это ширина
h это высота
Калькулятор
| Сторона 1 | прозрачный | |
| Сторона 2 | прозрачный | |
| Район: | ||
| Периметр: | ||
| Диагональ: | ||
Используйте калькулятор выше, чтобы вычислить свойства прямоугольника.
