Площадь сечения параллельного оси цилиндра и отсекающего от окружности
Ответ:
Объяснение:
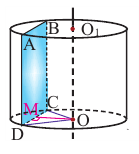
Сечение, параллельное оси цилиндра – прямоугольник ABCD.
Проведем ОН⊥АВ. ОН – расстояние от оси до плоскости сечения,
ΔАОВ равнобедренный (АО = ОВ как радиусы), значит ОН – высота и медиана, а в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине, значит
АВ = 2·ОН = 2 · 3 = 6 см
Sabcd = AB · AD = 6 · 6 = 36 см²
Сечение цилиндра плоскостью, параллельной его оси, есть квадрат?
Геометрия | 5 – 9 классы
Сечение цилиндра плоскостью, параллельной его оси, есть квадрат.
Эта плоскость отсекает от окружности основания дугу в 90 градусов .
Радиус цилиндра равен 4.
Найти площадь сечения.

Пусть сечение будет ABCD – квадрат, АВ – хорда основания.
Если дуга 90 град, то треугольник АВО – прямоугольный и равнобедренный, равные стороны равны радиусу.
Тогда АВ = 2 * R * sin45 град = 2 * 4 * корень(2) / 2 = 4 * корень(2).
S(сеч) = AB ^ 2 = 16 * 2 = 32.

Сечение цилиндра плоскостью , параллельного его оси, есть квадрат?
Сечение цилиндра плоскостью , параллельного его оси, есть квадрат.
Эта плоскость отсекает от окружности основания дугу в 90 грдс.
Радиус цилиндр равен 4 см.
Найдите площадь сечения.

Плоскость паралельная оси цилиндра отсекает от окружности основания дугу в 120 градусов?
Плоскость паралельная оси цилиндра отсекает от окружности основания дугу в 120 градусов.
Высота цилиндра равна 5 см радиус цилиндра равен 2 / 3 (два корень из трех) см.
Найдите площадь сечения.

В цилиндре параллельно оси проведена плоскость, отсекающая от окружности основания дугу 60градусов?
В цилиндре параллельно оси проведена плоскость, отсекающая от окружности основания дугу 60градусов.
Высота цилиндра 12см, расстояние от нее до секущей плоскости – 3см.
Найдите площадь сечения.

Сечение, параллельное оси цилиндра, отсекает от окружности основания дугу в 120 градусов?
Сечение, параллельное оси цилиндра, отсекает от окружности основания дугу в 120 градусов.
Найдите площадь боковой поверхности цилиндра, если площадь сечения равна Q.

Даю 50 баллов , помогите решить задачку?
Даю 50 баллов , помогите решить задачку!
Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 120°.
Высота цилиндра 5 см, радиус основания 2корень3 см .
Найти площадь сечения.

Сечение цилиндра, параллельное его оси, отсекает от окружности дугу в 120 градусов?
Сечение цилиндра, параллельное его оси, отсекает от окружности дугу в 120 градусов.
Радиус основания цилиндра равен R, а угол между диаганалью сечения и осью цилиндра равен 30 градусам.
Найдите объём цилиндра.

Сечение цилиндра плоскостью, параллельной его оси, есть квадрат?
Сечение цилиндра плоскостью, параллельной его оси, есть квадрат.
Эта плоскость отсекает от окружности основания дугу в 90 градусов .
Радиус цилиндра равен 4.
Найти площадь сечения.

Сечение цилиндра плоскостью, параллельной оси, удалено от нее на ?
Сечение цилиндра плоскостью, параллельной оси, удалено от нее на .
Это сечение отсекает в основании дугу в 60°.
Найдите площадь осевого сечения цилиндра, если площадь данного сечения равна 8.

Помогите, пожалуйста с задачей?
Помогите, пожалуйста с задачей.
В цилиндре параллельно оси проведено сечение отсекающее от окружности основания дугу в 102 градуса.
Угол между диагональю сечения и плоскостью основания цилиндра равен 60 * Вычислить объем цилиндра, если радиус основания цилиндра равен 18 см.

Сечение цилиндра, имеющее форму квадрата , параллельно его оси и отсекает от окружности дугу в 90 градусов?
Сечение цилиндра, имеющее форму квадрата , параллельно его оси и отсекает от окружности дугу в 90 градусов.
Площадь сечения равна 16 кв.
См . Найдите : а) площадь основания цилиндра ; б) угол между диагональю сечения и осью цилиндра.
Перед вами страница с вопросом Сечение цилиндра плоскостью, параллельной его оси, есть квадрат?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 – 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.
Площадь сечения параллельного оси цилиндра и отсекающего от окружности
Высота цилиндра равна 3, а радиус основания равен 13.
а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.
б) Найдите расстояние от плоскости сечения до центра основания цилиндра.
а) Пусть OO1 — ось цилиндра. Проведем AB и CD параллельно оси цилиндра. Проведем BD и AC. Так как через две параллельные прямые проходит единственная плоскость, то прямоугольник BDCA — искомое сечение (см. рис.). Расстояние от плоскости сечения до центра основания цилиндра, при котором площадь сечения равна 72, найдено в пункте б).
б) В этом прямоугольнике одна сторона будет равняться высоте цилиндра, а вторая — хорде окружности, лежащей в основании. Так как то где x — хорда AC. Проведем OH перпендикулярно AC. В силу того, что треугольник ACO равнобедренный, точка H также будет являться серединой AC. Тогда из прямоугольного треугольника, у которого гипотенуза — радиус OC, а один катет — половина этой хорды, находим второй катет OH по теореме Пифагора.
Таким образом, расстояние от центра окружности до сечения равно 5.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б)
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки |
2 |
| Имеется верное доказательство утверждения пункта а)
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, [spoiler title=”источники:”] http://geometria.my-dict.ru/q/517488_secenie-cilindra-ploskostu-parallelnoj-ego-osi/ http://ege.sdamgia.ru/problem?id=519683 [/spoiler] |
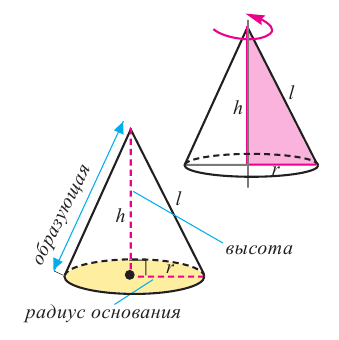
Напомним,
что цилиндр – это тело, полученное при вращении прямоугольника вокруг
прямой, проходящей через одну из его сторон.
Назовём
элементы цилиндра.
Основания
цилиндра – два равных круга радиуса .
Отрезок,
соединяющий окружности оснований и перпендикулярный основаниям, называется образующей
цилиндра и обозначается .
Все образующие цилиндра параллельны и равны.
Осью
цилиндра
называется прямая, проходящая через центры оснований. Она параллельна образующим.
Высота
цилиндра –
перпендикуляр, опущенный из любой точки одного основания на другое, или другими
словами, это расстояние между плоскостями оснований цилиндра. Образующая
цилиндра равна его высоте.
Радиусом
цилиндра называется радиус его основания.
Цилиндр
называется равносторонним, если его высота равна диаметру основания.
Осевым
сечением цилиндра называется сечение цилиндра плоскостью,
проходящей через его ось. Осевое сечение цилиндра – прямоугольник, две
стороны которого есть образующие цилиндра, а две другие – диаметры его
оснований.
Сечение,
параллельное оси цилиндра, является прямоугольником.
Сечение,
перпендикулярное оси цилиндра, является кругом, равным основаниям цилиндра.
Боковая
поверхность цилиндра может быть развёрнута в
прямоугольник со сторонами, одна из которых равна длине окружности основания,
другая – высоте цилиндра.
Площадь
боковой поверхности цилиндра можно вычислить по следующим
формулам:
,
,
,
где
–
длина окружности основания, –
высота цилиндра, –
радиус основания, –
образующая.
Площадь
полной поверхности цилиндра равна сумме площади боковой
поверхности цилиндра и двух площадей его оснований.
Тогда
площадь полной поверхности цилиндра можно вычислить по формуле:
,
где
–
радиус оснований цилиндра, –
его высота.
Объём цилиндра
равен произведению площади основания на высоту.
Тогда
его можно вычислить по формуле:
,
где
–
радиус оснований цилиндра, –
его высота.
Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.
Задача
первая. Радиус основания цилиндра равен см,
высота цилиндра равна диаметру его основания. Найдите площадь боковой
поверхности цилиндра.
Решение.
Задача
вторая. Найдите площадь сечения цилиндра плоскостью, параллельной
его оси и проходящей на расстоянии см
от неё, если площадь полной поверхности цилиндра равна см2,
а площадь боковой поверхности см2.
Решение.
Задача
третья. Призма со сторонами основания см
и см
и диагональю см
вписана в цилиндр. Найдите объём и площадь полной поверхности цилиндра.
Решение.
Задача
четвёртая. Плоскость, параллельная оси цилиндра, отсекает от
окружности основания дугу .
Диагональ полученного сечения равна и
удалена от оси цилиндра на расстояние .
Найдите объём цилиндра.
Решение.
Задача
пятая. В цилиндрический сосуд налили см3
воды. Уровень жидкости оказался равным см.
В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся
на см.
Найдите, чему равен объём детали. Ответ выразите в см3.
Решение.
Содержание:
Великий греческий ученый Архимед был очень взволнован, когда он обнаружил, что отношение площади поверхности шара и описанного около него цилиндра и отношение их объемов равно 2:3. Великий математик, физик, инженер, Архимед, среди всех своих работ самой значимой считал именно эту. Он завещал на своей могильной плите выгравировать доказательство данной теоремы. Из истории известно, что долгое время его родной город Сиракузы, располагающийся на Сицилии, противостоял римлянам именно благодаря оружию, которое изобрел Архимед. Поэтому при взятии города римский военачальники приказал сохранить ученому жизнь. Но римский воин, который не знал Архимеда в лицо, убил его. Великий философ и писатель Цицерон потратил много времени, чтобы отыскать могилу Архимеда (по историческим сведениям он нашел ее через 137 лет). Это дело Цицерона стало идеей для работ многих художников.
Определение фигур вращения
Гончарное ремесло позволяет создавать керамическую посуду из глины. Форму глиняной лепешке придают вращением вокруг оси. Затем полученную форму обжигают. Это ремесло живо и по сей день. В различных районах Азербайджана есть ремесленники, которые изготавливают керамическую посуду. Исследуйте принцип работы по которому кусок глины приобретает какую-либо форму.

Плоские фигуры (плоская часть ограниченная кривой), совершая один полный оборот вокруг определенной оси, образуют пространственные фигуры. Эта ось называется осью вращении.
Цилиндр, конус и сфера являются простыми пространственными фигурами, полученными при вращении.
Например, при вращении прямоугольного треугольника вокруг одного из катетов получается конус, при вращении прямоугольника вокруг стороны образуется цилиндр, а при вращении полукруга вокруг диаметра – шар.
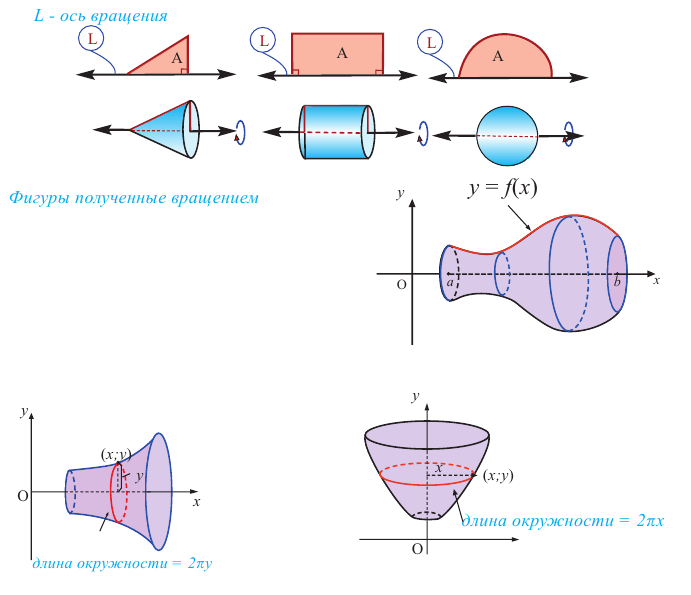
Цилиндр
Наглядно образование фигур вращения можно увидеть на примере вращающихся стеклянных дверей, которые мы часто видим в общественных зданиях, отелях и больницах. Прямоугольный слой двери, прикрепленный к неподвижной стойке, при вращении очерчивает цилиндр.
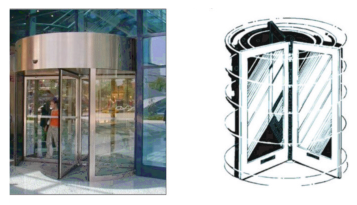
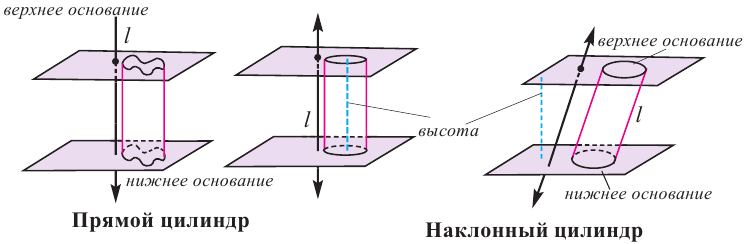
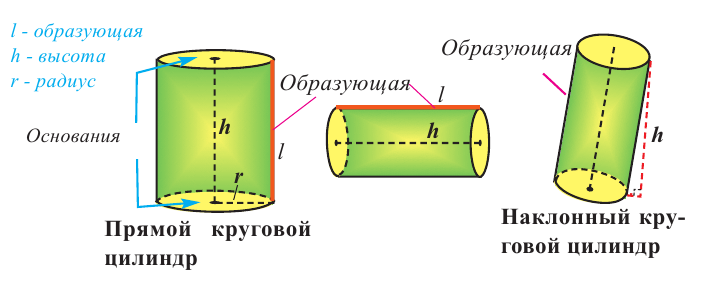
Цилиндром называется пространственная фигура, образованная двумя параллельными и конгруэнтными плоскими фигурами, которые совпадают при параллельном переносе, и отрезками, соединяющими соответствующие точки данных фигур. Плоские фигуры называются основаниями цилиндра, отрезки, соединяющие соответствующие точки основания называются образующими цилиндра. Если образующая перпендикулярна основанию, то цилиндр называется прямым, иначе – наклонным. Расстояние между основаниями называется высотой цилиндра.

На рисунках ниже изображены прямые и наклонные цилиндрические фигуры.
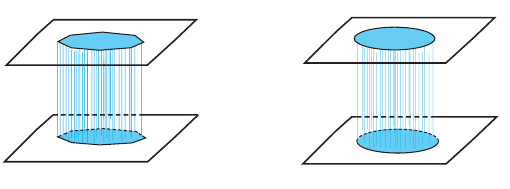
Сравнивая рисунки, изображенные ниже, можно сделать вывод, что призму можно рассматривать как частный случай цилиндра.
Прямой цилиндр, в основании которого лежит круг, называют прямым круговым цилиндром.
Далее, говоря о цилиндре, мы будем иметь в виду прямой круговой цилиндр. В любом другом случае будут отмечены его особенности.
Прямой круговой цилиндр также можно рассматривать как фигуру, полученную вращением прямоугольника вокруг одной из его сторон. Высота прямого кругового цилиндра равна его образующей. Радиусом цилиндра называется радиус круга в основании.
Вращая прямоугольник вокруг любой стороны, можно получить цилиндр, высота которого равна стороне прямоугольника.
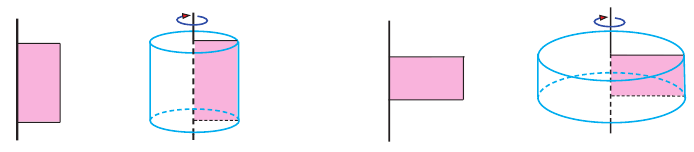
Прямая, проходящая через центры оснований прямого кругового цилиндра называется осью цилиндра.
Площадь поверхности цилиндра
Площадь боковой и полной поверхностей цилиндра.
Изобразите на листе бумаги рисунки разверток цилиндров различных размеров, вырежьте и склейте цилиндры.
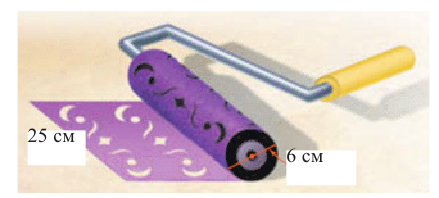
Мустафа красит стену цилиндрической кистью. Чтобы подсчитать время, потраченное на покраску, он захотел узнать, какую площадь покрывает кисть при одном полном обороте? Какие советы вы могли бы дать мальчику?
Так как кисть имеет цилиндрическую форму, то за один полный оборот кисть покрывает площадь в форме прямоугольника, равную боковой поверхности цилиндра.
Полная поверхность цилиндра находится но формуле схожей с формулой полной поверхности призмы. Полная поверхность цилиндра состоит из боковой поверхности и двух конгруэнтных кругов.
Боковую поверхность цилиндра с высотой 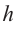 и радиусом
и радиусом 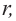 можно рассматривать как свернутый вокруг окружности прямоугольник со сторонами
можно рассматривать как свернутый вокруг окружности прямоугольник со сторонами 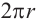 и
и 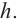

Боковая поверхность цилиндра равна произведению длины окружности основания и высоты.
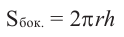
Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей оснований
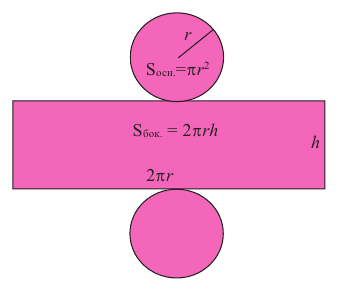
Пример №1
Найдите площадь полной поверхности цилиндра выстой 12 см и радиусом 5 см.
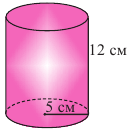
Решение: 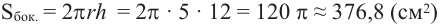
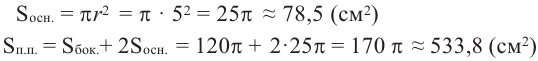
Пример №2
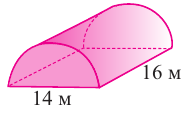
По данным рисунка, найдите площадь боковой поверхности прямого цилиндра, основанием которой являются полукруг.
Решение: 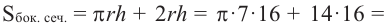
Пример №3
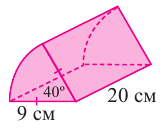
По данным на рисунке найдите площадь полной поверхности прямого цилиндра, основанием которой является круговой сектор с углом 40°.
Решение: известно, что 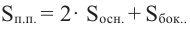
По формуле площади сектора:
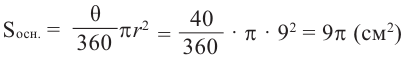
Боковая поверхность фигуры равна 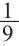 части боковой поверхности цилиндра с радиусом 9 см и высотой 20 см плюс площадь двух конгруэнтных прямоугольников размерами
части боковой поверхности цилиндра с радиусом 9 см и высотой 20 см плюс площадь двух конгруэнтных прямоугольников размерами 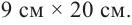
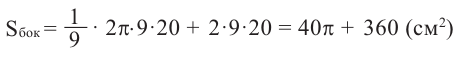
Таким образом,
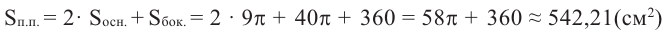
Конус
Конусом называется пространственная фигура, образованная всеми отрезками, соединяющими какую-либо плоскую фигуру с точкой, не принадлежащей данной плоскости. Плоскую фигуру называют основанием конуса, а точку –вершиной конуса.
Перпендикуляр, проведенный из вершины конуса на плоскость его основания, называется высотой конуса. Конус, в основании которого лежит круг, называется круговым конусом. Если ортогональная проекция вершины конуса лежит в центре основания, то конус называется прямым круговым конусом. Отрезок, соединяющий вершину конуса с любой точкой окружности основания кругового конуса, называется образующей конуса. В дальнейшем, говоря о конусе, будем иметь ввиду прямой круговой конус.
Конус можно рассматривать как фигуру, образованную вращением прямоугольного треугольника вокруг одного из катетов.
Прямая, выходящая из вершины конуса и проходящая через центр основания, называется осью конуса, радиус основания называется радиусом конуса. Для образующей, высоты и радиуса конуса справедливо отношение 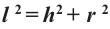 (по теореме Пифагора)
(по теореме Пифагора)
Сооружение конуса
Известно, что при сворачивании прямоугольника можно получить цилиндр. Скручивая круговой сектор можно соорудить конус.

Радиус сектора равен образующей конуса, а длина дуги сектора равна длине окружности основания.
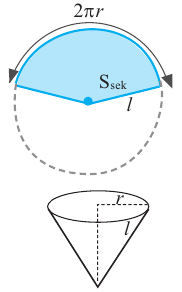
Боковая поверхность конуса, полная поверхность конуса
Поверхность конуса состоит из боковой поверхности и круга в основании. На рисунке показаны радиус основания  и образующая
и образующая 
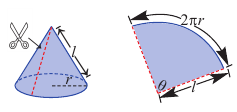
Боковая поверхность конуса – круговой сектор с радиусом 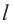 и соответствующим центральным углом
и соответствующим центральным углом 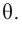
Значит, площадь сектора и есть площадь боковой поверхности.
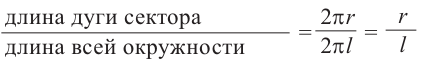
Значит, сектор составляет 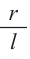 часть окружности.
часть окружности.
* Зная, что площадь круга 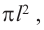 тогда
тогда 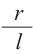 часть площади круга будет
часть площади круга будет 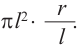
Значит,
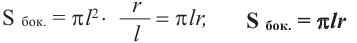
Боковая поверхность конуса равна произведению половины длины окружности основания и образующей.
* Площадь полной поверхности конуса
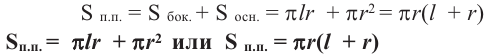
Пример №4
По рисунку найдите площадь боковой и полной поверхностей конуса.
Решение: Дано: 
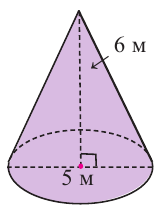
Найти: 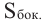 и
и 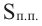
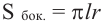 и
и 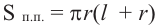
Чтобы найти образующую 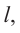 применим теорему Пифагора
применим теорему Пифагора
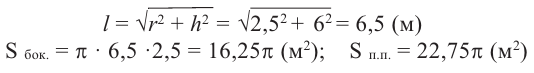
Сечения цилиндра и конуса плоскостью
Сечения поверхности конуса плоскостью (теория конических сечений) считались одной из вершин античной геометрии. Исследования Аполлония (3-й в.до н.э.) показали, что сечением плоскостью конуса, с бесконечной образующей (лучом) является: эллине (плоскость пересекает все образующие), парабола (плоскость сечения параллельна одной из образующих) или ветвь гиперболы (плоскость сечения параллельна двум образующим).
Сечения цилиндра плоскостью
Сечением цилиндра плоскостью, параллельной основанию, является круг. Сечение цилиндра плоскостью, проходящей через ось симметрии, называется осевым сечением. Осевое сечение цилиндра является прямоугольником со сторонами 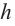 и
и 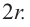 Значит,
Значит, 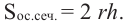 Цилиндр, осевое сечение которого является квадратом
Цилиндр, осевое сечение которого является квадратом 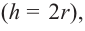 называется равносторонним цилиндром.
называется равносторонним цилиндром.
Сечения конуса плоскостью
Сечением конуса плоскостью, параллельной основанию, является круг. Сечение конуса, проходящее через ось конуса называется осевым сечением конуса. Это сечение является равнобедренным треугольником, боковые стороны которого являются образующими, а основание равно диаметру конуса: 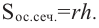 Если осевое сечение конуса является правильным треугольником
Если осевое сечение конуса является правильным треугольником 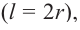 то конус называется равносторонним конусом.
то конус называется равносторонним конусом.
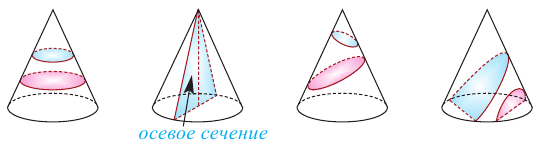
Пример №5
Сечением цилиндра плоскостью, проведенного параллельно оси цилиндра на расстоянии 3 см от оси, является квадрат, площадь которого равна 64  Найдите площадь полной поверхности цилиндра.
Найдите площадь полной поверхности цилиндра.
Решение: сначала найдем радиус и высоту цилиндра. По условию 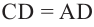 и
и 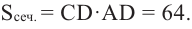 Отсюда
Отсюда 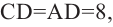 значит
значит 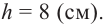 Из
Из 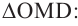
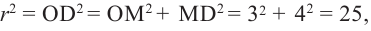 отсюда
отсюда 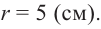 Таким образом,
Таким образом, 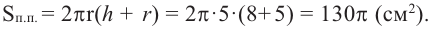
Усеченный конус и площадь поверхности
Усеченный конус
Если параллельно основанию прямого кругового конуса провести плоскость, то получим маленький конус и усеченный конус.

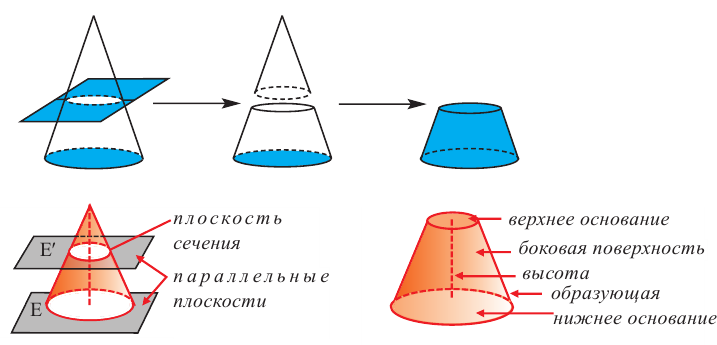
Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию.
Боковая поверхность усеченного конуса равна разности боковых поверхностей большого конуса и маленького конуса, отсеченного плоскостью, параллельной основанию, от большого конуса. Используя обозначения на рисунке, можно записать:
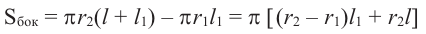
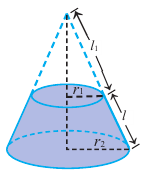
Из подобия треугольников запишем следующее отношение 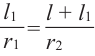
Тогда, подставив 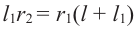 или
или 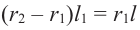 в формулу для нахождения боковой поверхности, получим:
в формулу для нахождения боковой поверхности, получим:
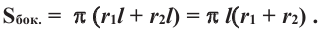
В данной формуле введем обозначение 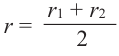 среднего радиуса
среднего радиуса
усеченного конуса. Тогда
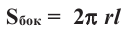
Полная поверхность усеченного конуса равна сумме боковой поверхности и площадей нижнего и верхнего оснований.
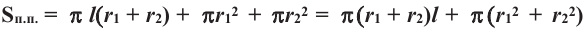
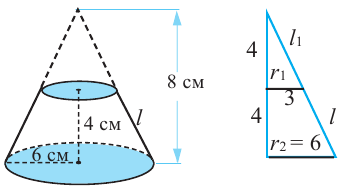
Пример №6
Конус высотой 8 см и радиусом 6 см рассечен плоскостью, параллельной основанию. Высота полученного усеченного конуса равна 4 см. Найдите площади боковой и полной поверхностей усеченного конуса
Решение: дано: 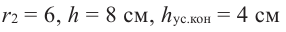
Найти:
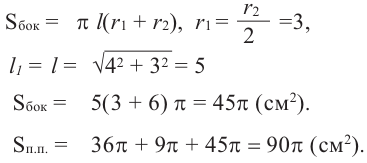
Площадь поверхности шара и его частей
Шаром называется множество всех точек пространства находящихся от данной точки на расстоянии, не больше данного. Данная точка называется центром шара, данное расстояние радиусом  шара.
шара.
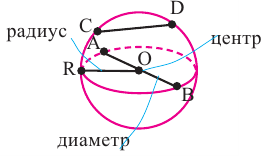
Множество всех точек, расположенных на расстоянии 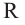 от центра шара, образует поверхность шара. Поверхность шара называется сферой. Прямая, соединяющая любые две точки на поверхности шара, называется хордой
от центра шара, образует поверхность шара. Поверхность шара называется сферой. Прямая, соединяющая любые две точки на поверхности шара, называется хордой 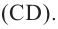 Хорда, проходящая через центр шара называется диаметром шара
Хорда, проходящая через центр шара называется диаметром шара 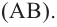
Шар получается, при вращении полукруга вокруг диаметра.
 Любое сечение шара плоскостью является кругом. Центр этого круга является основанием перпендикуляра, проведенного к плоскости и проходящего через центр шара. Если
Любое сечение шара плоскостью является кругом. Центр этого круга является основанием перпендикуляра, проведенного к плоскости и проходящего через центр шара. Если 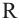 – радиус шара,
– радиус шара, 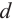 – расстояние между плоскостью и центром, а
– расстояние между плоскостью и центром, а 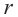 – радиус сечения, то получим:
– радиус сечения, то получим:
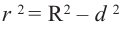
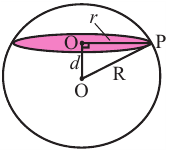
Пример №7
Шар радиуса 10 см пересечена плоскостью на расстояние
8 см от центра. Вычислите площадь сечения.
Решение: По условию 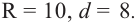
Тогда 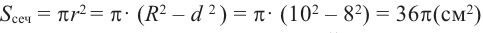
Сечение шара плоскостью, проходящей через центр шара, называется
большим кругом. Центр, радиус и диаметр большого круга равны
центру, радиусу и диаметру шара.

Также для шара известны следующие части:

Площадь поверхности шара
Площадь поверхности шара находится по формуле 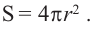 Здесь
Здесь 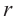 радиус шара.
радиус шара.
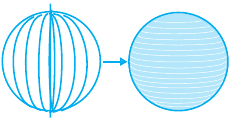
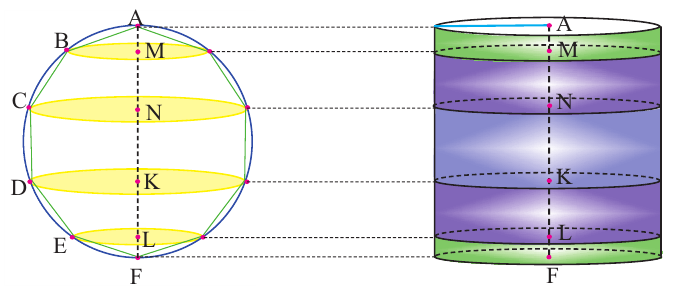
В окружность радиусом 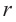 впишем правильный многоугольник. Поверхность шара, полученного при вращении относительно диаметра соответствующих кругов, можно рассматривать как сумму пределов боковых поверхностей фигур – конуса,усеченного конуса и цилиндра, образующие которых являются сторонами данного многоугольника.
впишем правильный многоугольник. Поверхность шара, полученного при вращении относительно диаметра соответствующих кругов, можно рассматривать как сумму пределов боковых поверхностей фигур – конуса,усеченного конуса и цилиндра, образующие которых являются сторонами данного многоугольника.
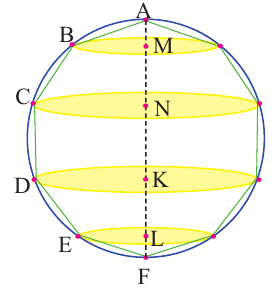
Покажем, что при вращении сторон многоугольника вокруг оси получается тело (конус, усеченный конус, цилиндр), площадь боковой поверхности которого равна площади боковой поверхности цилиндра, высота которого равна высоте данного тела, радиус основания равен апофеме многоугольника. Обозначим апофему многоугольника через 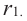
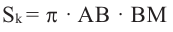 – площадь боковой поверхности конуса с образующей
– площадь боковой поверхности конуса с образующей 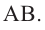 Так как
Так как 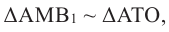 то
то 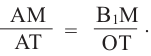 Умножим на 2 обе части равенства
Умножим на 2 обе части равенства
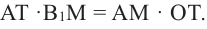 Учитывая, что
Учитывая, что 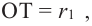
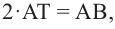 получим
получим 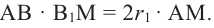 Значит,
Значит, 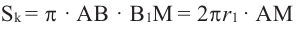
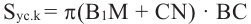 – площадь боковой поверхности усеченного конуса.
– площадь боковой поверхности усеченного конуса.
Зная, что 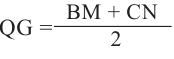 получим, что
получим, что 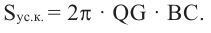
Так как 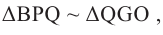 то
то 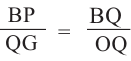
Умножим на 2 обе части равенства 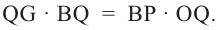 Учитывая,что
Учитывая,что
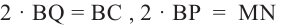 и
и 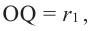 получим
получим 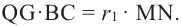
Значит, 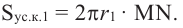
Понятно, что площадь боковой поверхности цилиндра с образующей 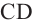 равна
равна 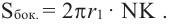 Аналогично получаем, что площадь боковых поверхностей усеченного конуса с образующей
Аналогично получаем, что площадь боковых поверхностей усеченного конуса с образующей 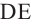 и конуса с образующей
и конуса с образующей 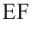 можно найти но формулам
можно найти но формулам 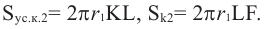 Таким образом, поверхность тела, полученного вращением многоугольника вокруг диаметра, равна :
Таким образом, поверхность тела, полученного вращением многоугольника вокруг диаметра, равна :
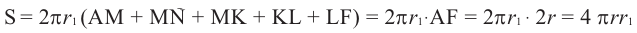
При бесконечном увеличении количества сторон многоугольника значение
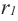 стремится к радиусу, а площадь поверхности полученного тела к площади
стремится к радиусу, а площадь поверхности полученного тела к площади
поверхности шара, т. е. 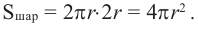
Площадь поверхности шара
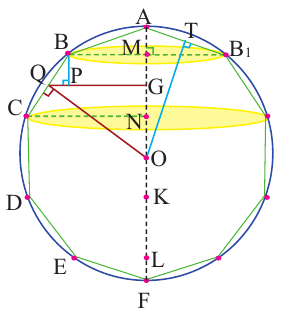
Доказательство Архимеда:
Пусть, в правильный многоугольник вписан круг, как показано на рисунке.

При вращении получается шар и покрывающее шар тело

Это тело состоит из двух усеченных конусов и цилиндра.

При увеличении количества сторон до бесконечности, тело будет стремится принять форму шара.

Найдя сумму поверхностей усеченных конусов и цилиндра, можно найти площадь поверхности шара. Рассмотрим осевое сечение одного из усеченных конусов. Пусть радиус средней окружности равен 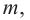 а высота
а высота 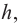 радиус шара
радиус шара 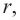 сторона многоугольника, описанного вокруг большего круга равна
сторона многоугольника, описанного вокруг большего круга равна 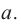 Площадь боковой поверхности усеченного конуса будет
Площадь боковой поверхности усеченного конуса будет 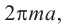 а также
а также 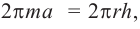 т. е. боковая поверхность усеченного конуса равна боковой поверхности цилиндра, радиус основания которого равен
т. е. боковая поверхность усеченного конуса равна боковой поверхности цилиндра, радиус основания которого равен 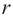 и высота
и высота 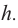
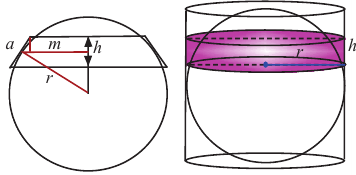
Значит, фигуру, описанную вокруг шара, можно принять за цилиндр. Отсюда получается, что площадь поверхности шара равна площади боковой поверхности цилиндра с радиусом основания 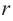 и высотой
и высотой 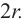
Т. е., 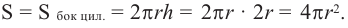

Площадь сегмента шара
Часть шара, отсекаемая плоскостью сечения называется сегментом. Круг, полученный при сечении плоскостью, называется основанием сегмента. Часть диаметра шара, перпендикулярного основанию сегмента, расположенная внутри него, называется высотой сегмента.
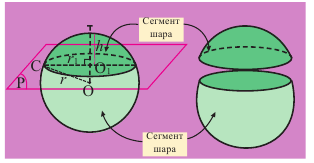
Из доказательства формулы поверхности шара, аналогично, можно показать, что для шара радиуса 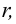 площадь сферической поверхности сегмента высотой
площадь сферической поверхности сегмента высотой 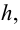 вычисляется по формуле
вычисляется по формуле 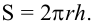
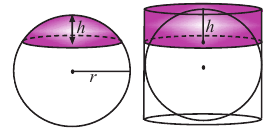
Площадь шарового пояса
Часть поверхности шара, расположенная между двумя параллельными плоскостями, называется шаровым поясом. Расстояние между параллельными плоскостями называется высотой шарового пояса.
Площадь поверхности шарового пояса можно найти, как разность площадей сегментов, отсекаемых параллельными плоскостями.
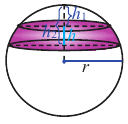
Площадь поверхности шарового пояса высотой  отсекаемого от шара радиуса
отсекаемого от шара радиуса 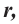 вычисляется по формуле
вычисляется по формуле 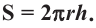
Пример №8
Радиус шара разбит на три равные части и через эти точки проведены перпендикулярные к радиусу плоскости. Зная, что радиус шара 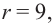 найдите площадь поверхности шарового пояса.
найдите площадь поверхности шарового пояса.
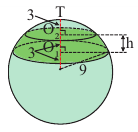
Решение: если 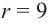 и
и  то площадь поверхности шарового пояса будет
то площадь поверхности шарового пояса будет 
Площади поверхностей подобных фигур
Отношение соответствующих линейных размеров подобных пространственных фигур постоянно и равно коэффициенту подобия.
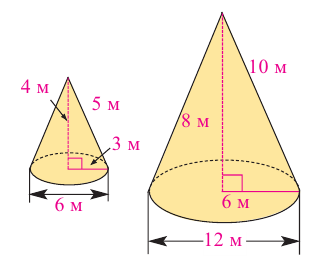
Например, чтобы проверить подобны ли конусы на рисунке, найдем отношение соответствующих размеров. Если эти конусы подобны, то отношение радиусов должно быть равно отношению высот.
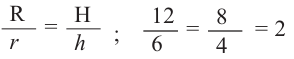
Значит эти конусы подобны и коэффициент подобия равен 2. Это говорит о том, что если все линейные размеры маленького конуса пропорционально увеличить в два раза, то получим конус, конгруэнтный большому конусу. Или наоборот, пропорционально уменьшив размеры большого конуса в два раза, получим конус, конгруэнтный маленькому. Если пропорционально увеличить или уменьшить размеры какой-либо фигуры, то можно получить подобные фигуры.
Отношение площадей подобных фигур равно квадрату отношения соответствующих линейных размеров или квадрату коэффициента подобия
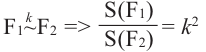
- Объем фигур вращения
- Длина дуги кривой
- Геометрические фигуры и их свойства
- Основные фигуры геометрии и их расположение в пространстве
- Вписанные и описанные многоугольники
- Площадь прямоугольника
- Объем пространственных фигур
- Объёмы поверхностей геометрических тел
Сечение цилиндра: определение, виды, его образующая
Содержание:
- Кратко о цилиндре
- Осевое сечение
- Как найти площадь сечения
- Осевое сечение наклонного цилиндра
-
Примеры задач
- Задача 1
- Задача 2
Кратко о цилиндре
Цилиндр — это геометрическая фигура, которая ограничена цилиндрической поверхностью и двумя плоскими окружностями.
Также можно сказать, что это тело вращения, возникающее при вращении прямоугольника вокруг его стороны.
Осевое сечение
Это сечение фигуры плоскостью, проходящей через ее ось. Оно является прямоугольником. Таким образом, любое сечение, параллельное оси цилиндра (и перпендикулярное его основанию), становится прямоугольником. Сторонами этой фигуры будет диаметр цилиндра и высота его оси.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как найти площадь сечения
Формула 1
(S = d*h,)
где (d) — диаметр, а (h) — высота всей фигуры.
Также есть формулы для расчета площади сечения, параллельного оси геометрического тела (но не пересекающего ее).
Формула 2
(S = a*h, )
где (a) — хорда.
Осевое сечение наклонного цилиндра
Сечение наклонного цилиндра по оси представляет собой параллелограмм. Его стороны нам уже известны: одна из них равна диаметру d, как и в случае с прямой фигурой. Другая — длина образующего отрезка. Ее мы можем обозначить буквой b.
Для точного определения всех параметров параллелограмма недостаточно знать только длины его сторон. Для расчета площади фигуры нам понадобится один из ее углов. Допустим, что острый угол между плоскостью и направляющий равен α. Тогда формула S параллелограмма будет выглядеть следующим образом:
(S = d * b * sin(α))
Примеры задач
Рассмотрим пару задач на осевое сечение с решениями.
Задача 1
Дан круглый прямой цилиндр. Его осевое сечение является квадратом. Вопрос: чему равна S сечения, если площадь поверхности всего цилиндра — 100 см²?
Решение
Чтобы найти S квадрата, нужно сначала определить радиус или диаметр окружности цилиндра. Для этого вспомним формулу для нахождения площади самого цилиндра:
(Sц = 2pi * r * (r + h))
Так как осевое сечение — квадрат, значит радиус основания в два раза меньше высоты фигуры. В таком случае, формула будет выглядеть так:
(Sц = 2pi * r * (r + 2r) = 6 * pi * r²)
Исходя из этого, будем выражать радиус:
(r = √(Sц / (6*pi)))
Если сторона квадратного сечения равна диаметру основания цилиндра, то для определения площади квадрата S используем формулу:
(S = (2*r)2 = 4*r2 = 2*Sц/ (3*pi))
Подставим известные данные ((Sц = 100см^2)) и получим площадь сечения (S = 21,23 см²).
Ответ: (S = 21,23 см²).
Задача 2
Дано: ABCD — осевое сечение цилиндра. Площадь сечения (Sc) равна (10 м²), а площадь основания (Sо— 5 м²). Найти высоту цилиндра.
Решение
Так как площадь основания — круг, то (Sо = pi * r²). Тогда (r = √(Sо/pi) = √(5/pi).)
Так как площадь сечения — прямоугольник, то (Sc = AB * BC = h * 2r.) Тогда (h = Sc/(2r) = 10/(2√(5/pi)) = 5√(pi/5) = √(5pi).)
Ответ: (h = √(5pi).)
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Математика,
вопрос задал BillSkarsgard,
9 месяцев назад
Ответы на вопрос
Ответил gal4enok0071
7
!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Русский язык,
1 месяц назад
Укажите, какое слово является формой слова ОБЛАКО. 1)в облаке 2)на облачке 3)облачность 4)облачное…
Английский язык,
1 месяц назад
перевести на английский язык . 1.Я купила машину 2.Я дома 3.Они в твоей школе 4.Вы хорошие …
Алгебра,
9 месяцев назад
ПОМОГИТЕ С АЛГЕБРОЙ СРОЧНО
варианты ответов для прил. м11
18
3
54
48.6…
Русский язык,
9 месяцев назад
подобрать однокореннные слова (4-5 слов) к словам: зелень, сад, мороз, игра, выделить окончание, основу, корень в именах сущ и прил.
Математика,
6 лет назад
реши задание: Грушевых деревьев 35, а яблонь только 7. Во сколько раз яблонь меньше?
История,
6 лет назад
Что сделал Столыпин хорошего и плохого. Задачи, которые ставил Столыпин в политическом плане и в экономическом, как он проводил реформы?
