Площадь диагонального сечения параллелепипеда
У прямоугольного параллелепипеда диагональное сечение представляет собой прямоугольник.

Значит, для нахождения его площади нужно воспользоваться формулой площади прямоугольника:
S = a * b.
Сторона a совпадает с диагональю основания параллелепипеда.
Длину диагонали основания можно найти по теореме Пифагора, поскольку данная диагональ разбивает прямоугольник на 2 прямоугольных треугольника и является в каждом из них гипотенузой.
BD² = AB² + AD². => BD = √(AB² + AD²).
Сторона b равна высоте параллелепипеда (боковому ребру).
Высоту параллелепипеда можно, например, найти по его объёму и площади основания.
У прямоугольного параллелепипеда основание – это прямоугольник, поэтому площадь основания равна произведению его длины и ширины (на рисунке это AB и AD).
BB1 = V / (AB * AD).
Далее рассмотрим несколько примеров.
**
Пример 1
Стороны основания прямоугольного параллелепипеда равны 12 см и 4 см, а высота равна 5 см.
Нужно найти площадь диагонального сечения.
S (сеч) = √(12² + 4²) * 5 = √140 * 5 = 2√35 * 5 = 10√35 см.
**
Пример 2
Стороны основания и высота прямоугольного параллелепипеда относятся как 1:2:3, а его объём равен 48 см².
Нужно найти площадь диагонального сечения.
1) Сначала найдём, чему равны стороны основания и высота.
V = abc = 48.
Пусть a = x, b = 2x, c = 3x.
x * 2x * 3x = 48.
6x³ = 48.
x³ = 8.
x = 2.
Таким образом, стороны основания равны 2 и 4 см соответственно, а высота равна 6 см.
2) Теперь всё решается так же, как и в 1 примере.
S (сеч) = √(2² + 4²) * 6 = √20 * 6 = 2√5 * 6 = 12√5 см.
Спрятать решение
Решение.
Введем обозначение (так как на середине диагонали параллелепипеда расположен центр сферы, описанной около параллелепипеда).
Если P и Q — середины боковых ребер DD1 и BB1, то прямая PQ параллельна BD и
Проведем прямую (MN) параллельную BD, CK перпендикулярную (MN), CF перпендикулярную KC1. Тогда
— заданный в условиях угол между секущей плоскостью и плоскостью основания. Так как высота CF перпендикулярна (AKC1), то
— заданный в условиях угол между диагональю CA1 и плоскостью сечения PAQC1. Так как
то
Поскольку
а прямая KC1 перпендикулярна AK, то площадь сечения PAQC1 равна
или
При и
получаем
Ответ:
Как найти сечение параллелепипеда
Сечения геометрических фигур имеют различные формы. У параллелепипеда сечение всегда представляет собой прямоугольник или квадрат. Оно имеет ряд параметров, которые могут быть найдены аналитическим способом.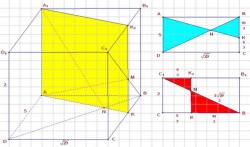
Через параллелепипед можно провести четыре сечения, которые представляют собой квадраты или прямоугольники. Всего он имеет два диагональных и два поперечных сечения. Как правило, они имеют разные размеры. Исключением является куб, у которого они одинаковы.
Перед тем как строить сечение параллелепипеда, составьте представление о том, что представляет собой эта фигура. Существует два вида параллелепипедов – обычный и прямоугольный. У обычного параллелепипеда грани располагаются под некоторым углом к основанию, а у прямоугольного они перпендикулярны ему. Все грани прямоугольного параллелепипеда представляют собой прямоугольники или квадраты. Из этого следует,что куб – это частный случай прямоугольного параллелепипеда.
У любого сечения параллелепипеда есть определенные характеристики. Основными из них являются площадь, периметр, длины диагоналей. Если из условия задачи известны стороны сечения или какие-либо иные его параметры, этого достаточно, чтобы найти его периметр или площадь. По сторонам определяются также диагонали сечений. Первый из этих параметров – площадь диагонального сечения.
Для того чтобы найти площадь диагонального сечения, нужно знать высоту и стороны основания параллелепипеда. Если даны длина и ширина основания параллелепипеда, то диагональ найдите по теореме Пифагора:
d=√a^2+b^2.
Найдя диагональ и зная высоту параллелепипеда, вычислите площадь сечения параллелепипеда:
S=d*h.
Периметр диагонального сечения тоже можно вычислять по двум величинам – диагонали основания и высоте параллелепипеда. В этом случае вначале найдите две диагонали (верхнего и нижнего оснований) по теореме Пифагора, а затем сложите с удвоенным значением высоты.
Если провести плоскость, параллельную ребрам параллелепипеда, можно получить сечение-прямоугольник, сторонами которого являются одна из сторон основания параллелепипеда и высота. Площадь этого сечения найдите следующим образом:
S=a*h.
Периметр этого сечения найдите аналогичным образом по следующей формуле:
p=2*(a+h).
Последний случай возникает, когда сечение проходит параллельно двум основаниям параллелепипеда. Тогда его площадь и периметр равны значению площади и периметра оснований, т.е.:
S=a*b – площадь сечения;
p=2*(a+b).
Площадь сечения параллелепипеда
Параллелепипед – это геометрическое тело, представляющее собой многогранник, у которого шесть граней и каждая из них прямоугольник. Основными математическими характеристиками параллелепипеда являются длины его ребер.
Сечение параллелепипеда – это изображение фигуры, образованной рассечением параллелепипеда плоскостью в поперечном или продольном направлении.

Формула для расчета площади бокового сечения параллелепипеда:
a – длина или ширина параллелепипеда;
b – высота параллелепипеда.
Формула для расчета площади диагонального сечения параллелепипеда:
b – высота параллелепипеда;
c – диагональ параллелепипеда.
Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади бокового или диагонального сечения параллелепипеда, если известны длина, диагональ и высота параллелепипеда. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения параллелепипеда (площадь бокового сечения параллелепипеда, площадь диагонального сечения параллелепипеда и площадь сечения параллелепипеда плоскостью).
Прямоугольный параллелепипед. Что это такое?

О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Определение параллелепипеда
Начнем с того, что узнаем, что такое параллелепипед.
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.
На рисунке два параллелограмма АВСD и A1B1C1D1. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.
Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.
Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.
Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.
Параллелепипед — это:
Свойства параллелепипеда
Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.
Вот 4 свойства параллелепипеда, которые необходимо запомнить:
- Противолежащие грани параллелепипеда равны и параллельны друг другу.
- Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
- Параллелепипед симметричен относительно середины его диагонали.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.
Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.
Свойства прямого параллелепипеда:
- Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
- Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
- Высота прямого параллелепипеда равна длине бокового ребра.
- Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
- Диагонали прямого параллелепипеда точкой пересечения делятся пополам.
На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.
Формулы прямого параллелепипеда:
- Площадь боковой поверхности прямого параллелепипеда
Sб = Ро*h
Ро — периметр основания
h — высота - Площадь полной поверхности прямого параллелепипеда
Sп = Sб+2Sо
Sо — площадь основания - Объем прямого параллелепипеда
V = Sо*h
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Свойства прямоугольного параллелепипеда
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.
- Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
- Противолежащие грани параллелепипеда попарно параллельны и равны.
- Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
- Диагонали прямоугольного параллелепипеда равны.
- В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы прямоугольного параллелепипеда:
- Объем прямоугольного параллелепипеда
V = a · b · h
a — длина, b — ширина, h — высота - Площадь боковой поверхности
Sбок = Pосн·c=2(a+b)·c
Pосн — периметр основания, с — боковое ребро - Площадь поверхности
Sп.п = 2(ab+bc+ac)
Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.
Доказательство теоремы:
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = d₁² + c² = a² + b² + c²
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
Куб: определение, свойства и формулы
Кубом называется прямоугольный параллелепипед, все три измерения которого равны.
Каждая грань куба — это квадрат.
Свойства куба:
- В кубе 6 граней, каждая грань куба — квадрат.
- Противолежащие грани параллельны друг другу.
- Все углы куба, образованные двумя гранями, равны 90°.
- У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
- Диагонали куба равны.
- Диагональ куба в √3 раз больше его ребра.
- Диагональ грани куба в √2 раза больше длины ребра.
Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.
Формулы куба:
- Объем куба через длину ребра a
V = a3 - Площадь поверхности куба
S = 6a2 - Периметр куба
P = 12a
Решение задач
Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.
Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a – длина, b – ширина, c – высота. Тогда a = 10, b = 5, c = 8.
Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) – сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) – суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) – сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) – сумма длин всех ребер прямоугольного параллелепипеда.
Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X – сумма длин ребер).
Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Нужно найти длину ребра A1B1.
В фокусе внимания треугольник BDD1.
Угол D = 90°.
По теореме Пифагора:
BD1 2 = DD1 2 + BD 2
BD 2 = BD1 2 – DD1 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 – AD 2 = (√17)2 — 4 2 = 1
A1B1 = AB = 1.
Задачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.
В треугольнике ADB угол A = 90°.
По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD1 2 = 52 + 25 = 77
BD1 = √77.
Самопроверка
Теперь потренируйтесь самостоятельно — мы верим, что все получится!
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.
Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Вычислите длину ребра AA1.
Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:
- прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
- параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
- основание прямоугольного параллелепипеда — прямоугольник;
- три измерения прямоугольного параллелепипеда: длина, ширина, высота;
- диагональ параллелепипеда равна сумме квадратов его измерений.
Прямоугольный параллелепипед
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$с$ – высота(она же боковое ребро);
$P_<осн>$ – периметр основания;
$S_<осн>$ – площадь основания;
$S_<бок>$ – площадь боковой поверхности;
$S_<п.п>$ – площадь полной поверхности;
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_<бок>=P_<осн>·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
Дополнительные сведения, которые пригодятся для решения задач:
$а$ – длина стороны.
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S=/<2>$, где $h_a$ – высота, проведенная к стороне $а$.
- $S=/<2>$, где $a,b$ – соседние стороны, $α$ – угол между этими соседними сторонами.
- Формула Герона $S=√$, где $р$ – это полупериметр $p=/<2>$.
- $S=p·r$, где $r$ – радиус вписанной окружности.
- $S=/<4R>$, где $R$ – радиус описанной окружности.
- Для прямоугольного треугольника $S=/<2>$, где $а$ и $b$ – катеты прямоугольного треугольника.
- Для равностороннего треугольника $S=/<4>$, где $а$ – длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ – смежные стороны. - Ромб.
$S=/<2>$, где $d_1$ и $d_2$ – диагонали ромба.
$S=a^2·sinα$, где $а$ – длина стороны ромба, а $α$ – угол между соседними сторонами. - Трапеция.
$S=<(a+b)·h>/<2>$, где $а$ и $b$ – основания трапеции, $h$ – высота трапеции. - Квадрат.
$S=a^2$, где $а$ – сторона квадрата.
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/pryamougolnyj-parallelepiped
http://examer.ru/ege_po_matematike/teoriya/pryamiugolnyi_parallelepiped
[/spoiler]
§ 12. Параллелепипед
12.1. Определение и свойства параллелепипеда
Определение. Призма, основание которой — параллелограмм, называется параллелепипедом (рис. 82).

Рис. 82
У параллелепипеда шесть граней и четыре диагонали.
Из определения следует, что у параллелепипеда все шесть граней — параллелограммы.
Грани параллелепипеда, не имеющие общих вершин, называются противолежащими (противоположными).
Параллельные рёбра параллелепипеда, не лежащие в одной грани, называются его противолежащими (противоположными) рёбрами.
Некоторые свойства параллелепипеда аналогичны свойствам параллелограмма.
Рассмотрим диагонали AC1 и В1D параллелепипеда ABCDA1B1C1D1 (рис. 83).

Рис. 83
Так как грани ABCD и В1С1CВ — параллелограммы, то равны и параллельны отрезки AD и BС, а также отрезки ВС и B1C1. Тогда на основании свойства транзитивности отношений параллельности и равенства отрезки AD и B1C1 равны и параллельны. Значит, четырёхугольник AB1C1D — параллелограмм. Диагонали AС1 и B1D параллелепипеда являются диагоналями этого параллелограмма, поэтому в точке О их взаимного пересечения каждая из них делится пополам.
Аналогично доказывается, что диагонали AC1 и ВD1, а также диагонали A1C и B1D пересекаются и точкой пересечения делятся пополам. А так как отрезок имеет только одну середину, то все четыре диагонали параллелепипеда пересекаются в одной точке О и делятся этой точкой пополам.
Тогда при центральной симметрии относительно точки О концы каждой из диагоналей параллелепипеда отображаются друг на друга, т. е. ZO(A) = C1, ZO(B) = D1, ZO(C) = A1, ZO(D) = B1, ZO(A1) = C, ZO(B1) = D, ZO(C1) = A, ZO(D1) = B. Это означает, что рёбра параллелепипеда центральной симметрией относительно точки О отображаются на противолежащие им рёбра, грани — на противолежащие им грани. А так как центральная симметрия — движение, при котором прямая и плоскость, не проходящие через центр симметрии, отображаются соответственно на параллельные прямую и плоскость, то как противоположные рёбра, так и противоположные грани параллелепипеда попарно равны и параллельны.
Кроме того, любая внутренняя точка параллелепипеда при симметрии SO отображается также на его внутреннюю точку. Следовательно, при центральной симметрии ZO параллелепипед ABCDA1B1C1D1 отображается на себя.
Таким образом, параллелепипед обладает следующими свойствами:
диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам;
точка пересечения диагоналей параллелепипеда является его центром симметрии;
противолежащие грани параллелепипеда попарно равны и параллельны.
Из сказанного выше следует, что любую грань параллелепипеда можно принять за его основание.
Определение. Параллелепипед называется прямым, если его боковые рёбра перпендикулярны плоскостям оснований (см. рис. 82, а), в противном случае параллелепипед называется наклонным (см. рис. 82, б, в).
Из определения следует, что все боковые грани прямого параллелепипеда — прямоугольники.
Определение. Прямой параллелепипед, основание которого — прямоугольник, называется прямоугольным.

Рис. 84
Таким образом, все грани прямоугольного параллелепипеда — прямоугольники (рис. 84). Из сказанного следует, что у прямоугольного параллелепипеда:
а) рёбра, сходящиеся в одной его вершине, попарно взаимно перпендикулярны;
б) любые две его грани либо параллельны, либо перпендикулярны;
в) каждое его ребро перпендикулярно тем граням, которые содержат лишь концы этого ребра.
Длины трёх рёбер прямоугольного параллелепипеда, исходящих из одной его вершины, называются измерениями прямоугольного параллелепипеда. У прямоугольного параллелепипеда три измерения.

Теорема 16. Квадpaт длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трёх его рёбер, исходящих из одной вершины.
Доказательство. Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1 (см. рис. 84) и найдём квадрат длины его диагонали А1С.
В △ АА1C (∠ А = 90°): А1C2 = АС2 +  ;
;
в △ ADC (∠ D = 90°): AC2 = AD2 + DC2.
Учитывая, что DC = AB, получаем: A1C2 = АB2 + АD2 +  . Теорема доказана. ▼
. Теорема доказана. ▼

Замечание. Эта теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому её иногда называют пространственной теоремой Пифагора.
У параллелепипеда есть ещё одно метрическое свойство, похожее на свойство параллелограмма: «Сумма квадратов длин всех диагоналей параллелепипеда равна сумме квадратов длин всех его рёбер». Это свойство легко доказывается векторным методом.
Изображения прямого и прямоугольного параллелепипедов имеют один и тот же вид. При этом ошибочным является зрительное восприятие того, что сечение прямого параллелепипеда плоскостью, которая проходит через противоположные стороны его оснований, всегда — прямоугольник. На самом деле, если прямой параллелепипед не прямоугольный, то его сечением плоскостью, проходящей через противолежащие стороны оснований, является параллелограмм, но не прямоугольник.

Рис. 85
Действительно, пусть ABCDA1B1C1D1 — прямой (но не прямоугольный) параллелепипед, четырёхугольник ABC1D1 — его сечение плоскостью, проходящей через противолежащие стороны АВ и C1D1 оснований (рис. 85).
Так как АВ = C1D1 и АВ || C1D1, то четырёхугольник ABC1D1 — параллелограмм. Докажем, что этот параллелограмм не может быть прямоугольником.
Предположим противное: пусть ABC1D1 — прямоугольник. Тогда АВ ⟂ ВС1 (как смежные стороны прямоугольника), АВ ⟂ BB1 (так как B1B ⟂ (ABC)), поэтому AB ⟂ (B1BC) (по признаку перпендикулярности прямой и плоскости) ⇒AB ⟂ BC ⇒ ABCD — прямоугольник ⇒ ABCDA1B1C1D1 — прямоугольный параллелепипед. Пришли к противоречию с условием теоремы. Значит, предположение неверно, и четырёхугольник ABC1D1 — параллелограмм.
Аналогично, сечение BCD1A1 — параллелограмм, но не прямоугольник. Утверждение доказано.

Рис. 86
ЗАДАЧА (2.090). В прямом параллелепипеде с основанием ABCD известно: АВ = 29 см, AD = 36 см, BD = 25 см, АА1 = 48 см. Найти площадь сечения AB1C1D.
Дано. ABCDA1B1C1D1 — прямой параллелепипед (рис. 86); АВ = 29 см, AD = 36 см, BD = 25 см, АA1 = 48 см.
Найти:  .
.
Решение. Имеем 292 + 362 ≠ 252 ⇒ AB2 + AD2 ≠ BD2 ⇒ △ ABD — не прямоугольный ⇒ ABCD — параллелограмм, но не прямоугольник. Это означает, что сечение AB1C1D — параллелограмм (докажите почему). Пусть C1E — высота этого параллелограмма, тогда (по теореме о трёх перпендикулярах) СЕ — высота основания ABCD.
Поэтому
 = AD•C1E, (1)△ CС1E (∠ C = 90°): C1E =
= AD•C1E, (1)△ CС1E (∠ C = 90°): C1E =  , (2)СЕ =
, (2)СЕ =  =
=  .(3)
.(3)
Таким образом, находим:
SABCD = 2s△ ABD =  = 720.
= 720.
Тогда из (3), (2) и (1) последовательно получаем СЕ =  = 20; C1E =
= 20; C1E =  = 52;
= 52;  = 36•52 = 1872 (см2).
= 36•52 = 1872 (см2).
Ответ: 1872 cм2.
ЗАДАЧА (2.100). Три ребра прямоугольного параллелепипеда, имеющие общую вершину, «видны» из точки пересечения его диагоналей под углами α, β и γ. Доказать, что cos α + соs β + соs γ = 1.
Дано: ABCDA1B1C1D1 — прямоугольный параллелепипед (рис. 87); O = A1C ∩ BD1; ∠ АОВ = α; ∠ BOC = β; ∠ B1OB = γ.
Дoкaзaть: cos α + cos β + cos γ = 1.

Рис. 87
Решение. Введём три некомпланарных вектора:  =
=  ,
,  =
=  ,
,  =
=  . Так как все диагонали прямоугольного параллелепипеда равны между собой, пересекаются в одной точке и делятся этой точкой пополам, то |
. Так как все диагонали прямоугольного параллелепипеда равны между собой, пересекаются в одной точке и делятся этой точкой пополам, то |  | = |
| = |  | = |
| = |  | = р. Тогда
| = р. Тогда
cos γ = cos ∠ ( ;
;  ) = cos ∠ (
) = cos ∠ ( ;
;  ) =
) =  =
=  .
.
Имеем △ OA1B1:  =
=  +
+  .
.
Ho  = –
= – = –
= – ,
,  =
=  =
=  –
–  =
=  –
–  .
.
Поэтому  = –
= –  +
+  –
–  . Значит,
. Значит,  •
• =
=  •(–
•(–  +
+  –
–  ).
).
Тогда cos α + cos β + cos γ =  +
+  +
+  =
=  =
=  =
=  = 1, что и требовалось доказать.
= 1, что и требовалось доказать.
ЗАДАЧА (2.106). Стороны основания прямого параллелепипеда равны 8 и 15 см и образуют угол в 60°. Меньшая из площадей диагональных сечений равна 130 см2. Найти: а) площадь второго диагонального сечения; б) площадь боковой поверхности параллелепипеда; в) площадь полной поверхности параллелепипеда; г) площади сечений параллелепипеда, проходящих через противолежащие стороны его верхнего и нижнего оснований.
Дано: ABCDA1B1C1D1 — прямой параллелепипед (рис. 88); AD = 8 см, АВ = 15 см, ∠ BAD = 60°,  = 130 см2.
= 130 см2.
Найти. a)  ; б) Sбок; в) Sполн; г)
; б) Sбок; в) Sполн; г)  ;
;  .
.
Pешение. ∠ BAD = 60°, значит, в параллелограмме ABCD диагонали AC и BD связаны неравенством BD < АС. Поэтому  = 130 и требуется найти
= 130 и требуется найти  . Так как АСС1A1 — прямоугольник (почему?), то
. Так как АСС1A1 — прямоугольник (почему?), то  = AC•AA1.
= AC•AA1.
Найдём длины отрезков АС и АА1.
△ ABD: BD2 = AB2 + AD2 – 2AB•AD сos A = 225 + 64 – 2•15•8•cos 60° = 169 ⇒ BD = 13.
△ АВС: АС2 = АВ2 + ВС2 – 2AB•ВС•cos В = 225 + 64 – 2•15•8•cos 120° = 409 ⇒ AC =  .
.
Далее,
 = BD•BB1 = 130 ⇒ BB1 = 130 : BD = 130 : 13 = 10.
= BD•BB1 = 130 ⇒ BB1 = 130 : BD = 130 : 13 = 10.

Рис. 88
Тогда:
а)  = AC•AA1 = 10
= AC•AA1 = 10 ;
;
б) Sбок = 2(AB + BC)•AA1 = 460;
в) Sполн = Sбок + 2Sосн;
Sосн = AB•AD•sin 60° = 60 .
.
Таким образом,
Sполн = 460 + 2•60 = 20•(23 + 6
= 20•(23 + 6 );
);
г) сечение ABC1D1 — параллелограмм (почему?). Пусть D1F — высота этого параллелограмма. Тогда  = АВ•D1F. Найдём длину D1F.
= АВ•D1F. Найдём длину D1F.
Имеем:
D1F ⟂ АВ, D1D ⟂ (АВС) ⇒ DF ⟂ АВ (по теореме о трёх перпендикулярах).
Поэтому DF = AD•sin 60° = 4 ,
,
△ DD1F (∠ D = 90°): D1F =  =
=  = 2
= 2  .
.
Тогда
 = 15•2
= 15•2  = 30
= 30  .
.
Аналогично, сечение BCD1A1 — параллелограмм. Если D1E — высота этого параллелограмма, то DE ⟂ BC. Поэтому ∠ DED1 = ϕ — угол между плоскостью сечения BCD1A1 и плоскостью основания ABCD. Так как основание ABCD является ортогональной проекцией сечения ВСD1A1, то  = Sосн : cos ϕ. Найдём cos ϕ.
= Sосн : cos ϕ. Найдём cos ϕ.
△ DEC: DE = DC•sin 60° =  .△ DED1: tg ϕ =
.△ DED1: tg ϕ =  = 10 :
= 10 :  =
=  ⇒ cos ϕ =
⇒ cos ϕ =  .
.
Откуда  = 60
= 60 :
:  = 20
= 20 .
.
Ответ: а) 10 cм2; б) 460 см2; в) 20•(23 + 6
cм2; б) 460 см2; в) 20•(23 + 6 ) cм2; г) 30
) cм2; г) 30  см2; 20
см2; 20  см2.
см2.
ЗАДАЧА (2.108). Диагональ прямоугольного параллелепипеда равна d и образует с меньшей боковой гранью угол α, а с плоскостью основания — угол ϕ. Найти площадь боковой поверхности параллелепипеда.

Рис. 89
Дано: ABCDA1B1C1D1 — прямоугольный параллелепипед; BD1 = d;
∠ DBD1 = ϕ; ∠ D1BC1 = α (рис. 89).
Найти: Sбок.
Решение. Sбок = 2•( +
+  ).
).
Так как все боковые грани прямоугольного параллелепипеда — прямоугольники, то
 = AB•BB1;
= AB•BB1;  = BC•BB1.
= BC•BB1.
Найдём стороны основания и боковое ребро параллелепипеда.
Вследствие того, что DD1 ⟂ (АВC) и D1C1 ⟂ (BCC1), имеем:
в △ BDD1 (∠ BDD1 = 90°): BD = d•cos ϕ, DD1 = d•sin ϕ;
в △ BC1D1 (∠ BC1D1 = 90°): ВС1 = d•cos α, C1D1 = d•sin α.
Тогда
△ BCD (∠ BCD = 90°): BC2 = BD2 – CD2 =
= d2 соs2 ϕ – d2 sin2 α ⇒ ВС = d  .
.
Так как AB = C1D1, BB1 = DD1, то
 = d•sin α•d•sin ϕ = d2•sin α•sin ϕ;
= d•sin α•d•sin ϕ = d2•sin α•sin ϕ;
 = d
= d •d•sin ϕ =
•d•sin ϕ =
= d2•sin ϕ  .
.
Преобразуем
cos2 ϕ – sin2 α =  –
–  =
=  =
=
= cos (ϕ + α) cos (ϕ – α).
Тогда
Sбок = 2•( +
+  ) =
) =
= 2•(d2•sin α•sin ϕ + d2•sin ϕ• ) =
) =
= 2d2•sin ϕ (sin α +  ).
).
Ответ: 2d2•sin ϕ (sin α +  ).
).
Определение. Прямоугольный параллелепипед, у которого все рёбра равны, называется кубом.
Из этого определения следует, что у куба все грани — равные квадраты.
12.2. Объём параллелепипеда
Объём параллелепипеда, как и любой другой призмы, равен произведению площади его основания на высоту.
Ранее отмечалось, что у параллелепипеда, в отличие от любой другой призмы, любая грань может быть принята за его основание. При этом каждой грани параллелепипеда, принятой за его основание, соответствует высота параллелепипеда, опущенная на эту грань. Таким образом:
Vпаралл = S1•h1 = S2•h2 = S3•h3,
где S1, S2, S3 — площади трёх граней параллелепипеда, имеющих общую вершину, h1, h2, h3 — высоты параллелепипеда, опущенные на эти грани.
Этим соотношением часто пользуются при решении различных задач.
ЗАДАЧА (2.164). Грани параллелепипеда — равные ромбы со стороной а и острым углом в 60°, расположенные так, что три острых плоских угла трёх его граней имеют общую вершину. Найти объём параллелепипеда.
Дано: ABCDA1B1C1D1 — параллелепипед, все грани которого — равные ромбы; АВ = a, ∠ A1AB = ∠ A1AD = ∠ BAD = 60° (рис. 90).
Найти: объём параллелепипеда.
Решение. Объём V данного параллелепипеда найдём по формуле: V = Sосн•h = SABCD•A1H, где A1H — высота параллелепипеда.
Прежде всего, докажем, что основание Н высоты А1Н параллелепипеда лежит на диагонали АС ромба ABCD.

Рис. 90
В самом деле, так как все грани параллелепипеда — равные ромбы, то высоты всех граней равны. Пусть отрезки A1K и А1M — высоты граней AA1D1D и AA1B1B (см. рис. 90), где точка K — середина AD, М — середина АВ (докажите почему).
Так как отрезок А1Н — перпендикуляр к плоскости основания параллелепипеда, то по теореме о трёх перпендикулярах HK ⟂ AD, HM ⟂ AB. При этом НK = HM (как проекции равных наклонных), т. е. точка H равноудалена от сторон угла BAD, значит, точка Н принадлежит диагонали AC ромба ABCD, которая является биссектрисой угла BAD. Более того, так как точка K — середина AD и точка М — середина АВ, то в точке Н пересекаются медианы BK, DM и АО треугольника ABD.
Из сказанного следует важный вывод: изображение заданного параллелепипеда следует начинать с построения нижнего основания АВСD и точки Н = АC ∩ ВK (где точка K — середина AD); вершина A1 выбирается на перпендикуляре, проведённом через точку Н к плоскости основания.
Теперь нетрудно найти длину высоты А1H.
В правильном △ ABD: АН =  АО =
АО =  . В прямоугольном △ AA1H: A1H =
. В прямоугольном △ AA1H: A1H =  =
=  =
=  . А так как SABCD = AB2•sin 60° =
. А так как SABCD = AB2•sin 60° =  , то V =
, то V =  •
• =
=  .
.

Ответ:  .
.
