Как найти площадь сечения параллелепипеда через вершины

автор вопроса выбрал этот ответ лучшим

Задания

Версия для печати и копирования в MS Word

Ещё пару задачек связанных с параллелепипедами. Данные задания от остальных, рассмотренных ранее, отличаются тем, что здесь требуется найти площадь сечения.

Сами вычисления минимальны. Основная трудность у некоторых может возникнуть именно в построении самого сечения. Что ж, все рекомендации даны ниже, приступим:

315131. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁  ребро AB = 2, ребро AD равно корню из пяти, ребро AA₁ = 2. Точка K  — середина ребра BB₁. Найдите площадь сечения, проходящего через точки A₁, D₁ и K.

Построим параллелепипед, обозначим вершины и точку К. Затем построим плоскость, проходящую через точки A₁, D₁ и K:

Сечением является прямоугольник с соседними сторонами A₁D₁ и A₁K (обозначен синим контуром). Для того, чтобы найти его площадь необходимо знать отрезок A₁K. 

Отрезок A₁D₁ = AD,  так как параллельные рёбра у параллелепипеда равны:

Найдём A₁K. По теореме Пифагора:

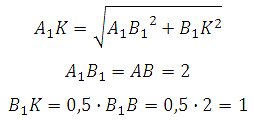
Значит

Таким образом, можем найти площадь сечения:

*Плоскость сечения обычно задаётся тремя точками, поэтому есть «соблазн» по данным трём точкам построить треугольник и найти его площадь. Совет: мысленно представьте, что как будто бы вы делаете срез ножом. Запомните, что  у фигуры, которая является сечением, все её стороны должны лежать на гранях и рёбрах заданного тела.

**И ещё. Если в прямоугольном параллелепипеде плоскость проходит через любое его ребро и рассекает этот параллелепипед, то сечением всегда  будет являться прямоугольник.

Ответ: 5

316552. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁   известны длины рёбер: AB = 24, AD = 10, AA₁ = 22. Найдите площадь сечения, проходящего через вершины A₁, A₁ и C.

Построим параллелепипед, обозначим вершины. Затем построим плоскость, проходящую через точки A₁, А₁ и С:

Сечением является прямоугольник (обозначен синим цветом). Для того, чтобы найти его площадь необходимо найти АС. Ребро AA₁ нам известно.

По теореме Пифагора:

Таким образом, можем найти площадь сечения:

Ответ: 572

Ещё раз повторюсь: для того, чтобы задать плоскость достаточно три точки (и в задачах, обычно, она так и задаётся), но само сечение может проходить и через 4 и через 5 и более точек, лежащих на рёбрах тела ( такие тела  как призмы, пирамиды, параллелепипеды).

Поэтому будьте внимательны при построении сечения. Кроме того, помните, что сечение это всегда плоская фигура!

*Конечно, существуют и другие способы задания сечений, но об этом не здесь.

На этом всё! Успеха вам! 

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Здравствуйте, уважаемые читатели.

Здесь будет решение последней задачи С2 из реального ЕГЭ 2013 года. Решать будем то же задание, что и выпускники восточного региона.

В прямоугольном параллелепипеде `ABCDA_1B_1C_1D_1` известны ребра `AB = 8, AD = 7, AA_1 = 5`. Точка `W` принадлежит ребру `DD_1` и делит его в отношении `1:4`, считая от вершины `D`. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки `C, W` и `A_1`.

Задача, конечно, элементарная, однако неподготовленного школьника может легко сбить с толку. Итак, приступим.

Исходный параллелепипед выглядит следующим образом:

Построение сечения

• Отметим на ребре `DD_1` точку `W`.
• Проведем отрезок `A_1W`.
• Через точку `C` проведем прямую, параллельную `A_1W`. Пусть она пересекает `BB_1` в точке `N`.

Параллелограмм `A_1WCN` — искомое сечение. (Убедиться, что полученный четырехугольник является параллелограммом, предлагаю самостоятельно.)

Более подробно за описанием построения можно обратиться к Сибирскому варианту ЕГЭ.

Найдем стороны получившегося параллелограмма.

Поиск сторон

 Рассмотрим грань `AA_1D_1D` исходного параллелепипеда.

Сторона `A_1D_1 = 7` известна по условию, `D_1W = 4` также по условию.

По теореме Пифагора `A_1W = sqrt{49 + 16} = sqrt{65}`.

Теперь рассмотрим грань `DD_1C_1C`.

Аналогично по теореме Пифагора находим `WC=sqrt{64+1} = sqrt{65}`.

Теперь стало понятно, что наше сечение — ромб. Давайте вынесем его на отдельный рисунок.

Его площадь может быть удобно искать как половину произведения диагоналей, но сейчас мы пойдем немного другим путем: разобьем ромб на два одинаковых треугольника и найдем площадь одного из них — половины ромба.

Итак, `A_1C` — это диагональ исходного прямоугольного параллелепипеда. `A_1C = sqrt{5^2 + 8^ 2 + 7^2} = sqrt{138}`.

Чтобы найти площадь `triangle A_1WC`, найдем высоту `WH`. Заметим, что `WH` это еще и медиана, т. к. `triangle A_1WC` равнобедренный, значит `HC = frac{sqrt{138}}{2}`.

По теореме Пифагора получим: `WH = sqrt{65 – dfrac{138}{4}} = sqrt{dfrac{61}{2}}`.

Теперь можно найти `S_{triangle A_1WC}`.

$$S_{triangle A_1WC} = sqrt{138} cdot  sqrt{frac{61}{2}} cdot frac{1}{2} = sqrt{frac{138cdot 61}{2}} = sqrt{69cdot 61} = sqrt{4209}$$.

Осталось умножить полученную площадь на два, чтобы получить площадь сечения. Замечательный ответ 🙂

Ответ

`2sqrt{4209}`.

А теперь внимание! В решении была допущена ошибка. Кто готов найти ее?

Если решение понятно, то дружно ставим лайки, и пишем комментарии, если непонятно.