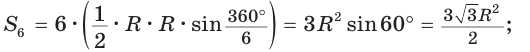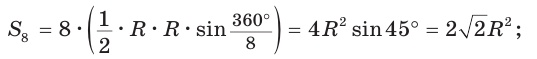На практике часто возникают задачи, которые требуют умения строить сечения геометрических фигур различной формы и находить площади сечений. В данной статье рассмотрим, как строятся важные сечения призмы, пирамиды, конуса и цилиндра, и как рассчитывать их площади.
Объемные фигуры
Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.
 Вам будет интересно:Что значит слыть: толкование, синонимы
Вам будет интересно:Что значит слыть: толкование, синонимы
Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.
Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).
Цилиндр
Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.

Для этой фигуры существует три важных типа сечения:
- круглое;
- прямоугольное;
- эллиптическое.
Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.
Площадь круглого сечения рассчитывается по формуле:
S1 = pi*r2
Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:
S2 = 2*r*h
Сечения конуса
Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:
- круглое;
- эллиптическое;
- параболическое;
- гиперболическое;
- треугольное.
Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.
Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:
S1 = pi*r2*z2/h2
Здесь z – это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z < h, то площадь изучаемого сечения будет всегда меньше ее значения для основания.
Треугольное получается, когда плоскость пересекает фигуру по ее оси вращения. Формой получившегося сечения будет равнобедренный треугольник, сторонами которого являются диаметр основания и две образующие конуса. Как находить площадь сечения треугольного? Ответом на этот вопрос будет следующая формула:
S2 = r*h
Это равенство получается, если применить формулу для площади произвольного треугольника через длину его основания и высоту.
Сечения призмы
Призма – это большой класс фигур, которые характеризуются наличием двух одинаковых параллельных друг другу многоугольных оснований, соединенных параллелограммами. Любое сечение призмы – это многоугольник. В виду разнообразия рассматриваемых фигур (наклонные, прямые, n-угольные, правильные, вогнутые призмы) велико и разнообразие их сечений. Далее рассмотрим лишь некоторые частные случаи.

Если секущая плоскость параллельна основанию, то площадь сечения призмы будет равна площади этого основания.
Если плоскость проходит через геометрические центры двух оснований, то есть является параллельной боковым ребрам фигуры, тогда в сечении образуется параллелограмм. В случае прямых и правильных призм рассматриваемый вид сечения будет представлять собой прямоугольник.
Пирамида
Пирамида – это еще один многогранник, который состоит из n-угольника и n треугольников. Пример треугольной пирамиды показан ниже.

Если сечение проводится параллельной n-угольному основанию плоскостью, то его форма будет в точности равна форме основания. Площадь такого сечения вычисляется по формуле:
S1 = So*(h-z)2/h2
Где z – расстояние от основания до плоскости сечения, So – площадь основания.
Если секущая плоскость содержит вершину пирамиды и пересекает ее основание, то мы получим треугольное сечение. Для вычисления его площади необходимо обратиться к использованию соответствующей формулы для треугольника.

Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
65
Добавлен:
15.05.2015
Размер:
406.75 Кб
Скачать
ПРИМЕНЕНИЕ ТЕОРЕМЫ О ПЛОЩАДИ ОРТОГОНАЛЬНОЙ ПРОЕКЦИИ МНОГОУГОЛЬНИКА ПРИ РЕШЕНИИ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ
Бардушкин В.В., Белов А.И., Ланцева И.А., Прокофьев А.А., Фадеичева Т.П.
Существует несколько методов решения стереометрических задач на вычисление площадей сечений, поверхностей многогранников и углов (между плоскостями, между прямой и плоскостью и т.д.). Эти методы достаточно подробно рассмотрены в школьных учебниках, изложены в различных пособиях по стереометрии. Так, например, при вычислении площадей широко применяется подход, основанный на разбиении многоугольника на части (на треугольники и четырёхугольники). Если в каждой из частей удаётся вычислить длины сторон (или диагоналей четырёхугольника) и какие-нибудь углы, то можно по известным формулам найти их площади, а значит, решить задачу. Довольно большое значение придаётся векторно-координатному методу решения подобных задач. Однако, на наш взгляд, многие из авторов-составителей не уделяют должного внимания методу вычисления площадей и углов, связанному с ортогональным проектированием многоугольника на некоторую плоскость. Накопленный нами опыт преподавания стереометрии, частично отражённый в настоящей статье, показывает, что изучение такой темы как «Площадь ортогональной проекции многоугольника» повышает у школьников интерес к предмету, стимулирует освоение ими других серьёзных тем по геометрии, что в итоге ведёт к интенсификации всего процесса обучения.
1. Теорема о площади ортогональной проекции плоской фигуры
Параллельное проектирование, при котором проектирующие прямые перпендикулярны к плоскости проекций, называется ортогональным.
Ортогональной проекцией фигуры на данную плоскость называют множество точек пересечений с этой плоскостью перпендикулярных к ней прямых, проходящих через все точки этой фигуры. В общем случае справедлива следующая теорема.
Если фигура Ф с площадью SФ лежит в плоскости , а фигура Ф с площадью SФ является ортогональной проекцией фигуры Ф на плоскость , то имеет место равенство
SФ SФ cos ,
где – угол между плоскостями и .
В школьном курсе стереометрии приведённая теорема формулируется и доказывается лишь для случая, когда проектируемая фигура – плоский многоугольник. В этом случае формулировка имеет вид:
Площадь Sпр ортогональной проекции многоугольника на плоскость равна произве-
дению его площади Sмн , умноженной на косинус угла между плоскостью много-
угольника и плоскостью проекции: Sпр Sмн cos .
2. Применение теоремы о площади ортогональной проекции многоугольника при нахождении площадей сечений
Эту теорему с успехом применяют, прежде всего, при вычислении площадей сечений многогранников. Данный подход используется в ситуациях, когда нахождение площади Sпр ортогональной проекции многоугольника, полученного в сечении, и угла между
секущей плоскостью и плоскостью проектирования сопряжено с меньшими трудностями, чем непосредственное вычисление площади сечения. В этом случае
|
Sсечения |
S |
пр |
. |
(1) |
||
|
cos |
||||||
1
В примерах 1 – 4 иллюстрируется это основное применение теоремы о площади ортогональной проекции многоугольника.
|
B1 |
C1 |
Пример 1. В правильной четырёхугольной призме |
|||||||||
|
сторона основания равна 4 см. Через диагональ основа- |
|||||||||||
|
A1 |
D1 |
ния под углом 45 |
к плоскости основания проведена |
||||||||
|
M |
плоскость, пересекающая боковое ребро. Найти пло- |
||||||||||
|
щадь сечения. |
|||||||||||
|
Решение. Согласно условию задачи, площадь ор- |
|||||||||||
|
B |
тогональной проекции сечения на плоскость основания |
||||||||||
|
45 |
C |
призмы равна половине его площади (см. рис. 1), т.е. |
|||||||||
|
O |
42 |
8 (см2). Тогда, используя формулу (1), полу- |
|||||||||
|
A |
D |
Sпр |
|||||||||
|
2 |
|||||||||||
|
чаем: Sсечения |
Sпр |
2 |
|||||||||
|
Рис. 1 |
8 2 (см ). |
||||||||||
cos45
Ответ: 8
 2 см2.
2 см2.
Пример 2. Стороны основания прямого параллелепипеда равны 4 и 5, угол между ними равен 30°. Найти площадь сечения параллелепипеда плоскостью, пересекающей все его боковые рёбра и образующей с плоскостью основания угол в 45°.
|
Решение. Для нахождения площади сечения воспользуемся формулой (1). Поскольку |
||||||||
|
B1 |
C1 |
секущая плоскость пересекает все боковые рёбра |
||||||
|
прямого параллелепипеда ABCDA BC D , то ортого- |
||||||||
|
A1 |
D1 |
1 |
1 |
1 |
1 |
|||
|
N |
нальной проекцией сечения MQNP является паралле- |
|||||||
|
Q |
лограмм ABCD (см. рис. 2). Отметим, что MQNP так- |
|||||||
|
же является параллелограммом, так как MQ||PN и |
||||||||
|
P |
||||||||
|
M |
MP||QN по свойству параллельных плоскостей (если |
|||||||
|
B |
C |
две параллельные плоскости пересечены третьей, то |
||||||
|
A |
30 |
D |
линии пересечения параллельны). |
|||||
|
Найдем площадь параллелограмма ABCD. Пусть, |
||||||||
|
Рис. 2 |
для определённости, AB 4, AD 5, |
BAD 30 , |
||||||
|
тогда SABCD AB AD sin BAD 10. |
||||||||
|
SABCD |
||||||||
|
Поскольку SMQNP |
, где 45 – угол между плоскостью сечения и основани- |
|||||||
|
cos |
ем параллелепипеда (на рис. 2 этот угол не показан), то SMQNP 10
 2 .
2 .
Ответ: 10
 2 .
2 .
Пример 3. Дан куб ABCDA1B1C1D1 с ребром, равным a. На рёбрах основания AB и AD взяты соответственно точки M и N так, что AM :MB 2:1 и AN :ND 2:1. Найти площадь сечения куба плоскостью, проходящей через точки M, N и C1 .
Решение. Приведём два способа решения этой задачи. Первый способ основан на разбиении многоугольника, полученного в сечении, на части и вычислении по отдельности площадей этих частей, а второй – на использовании теоремы о площади ортогональной проекции многоугольника. Читатель сам сможет определить, какой из предложенных подходов предпочтительнее.
Прежде чем перейти к решению задачи этими двумя способами, используя метод следов, построим сечение куба плоскостью, проходящей через точки M, N и C1. Соединим вначале точки M и N, поскольку они лежат в одной плоскости ABC (см. рис. 3а). Прямая MN лежит в плоскости ABC и пересекает прямые BC и DC в точках P и L соответственно.
2
Точка P принадлежит не только плоскости нижнего основания куба, но и плоскости грани BB1C1 (как и точка C1), поэтому, соединив P и C1, получим на ребре BB1 принадлежащую сечению точку F. Далее, точка L принадлежит не только плоскости нижнего основания куба, но и плоскости грани DD1C1 (как и точка C1), поэтому, соединив L и C1, получим на ребре DD1 принадлежащую сечению точку T. В завершение построения соединим в грани
AA1B1 точки M и F, а в грани AA1D1 точки T и N. Таким образом, сечением куба
ABCDA1B1C1D1 является пятиугольник MFC1TN .
|
B1 |
C1 |
||||||||
|
B1 |
A1 |
D1 |
|||||||
|
C1 |
B1 |
||||||||
|
C1 |
|||||||||
|
A1 |
D1 |
||||||||
|
A1 |
D1 |
F |
|||||||
|
F |
M |
B |
C |
||||||
|
P |
F |
T |
|||||||
|
B |
|||||||||
|
B |
O |
D |
|||||||
|
M |
T |
C |
T |
A |
N |
||||
|
M |
C |
||||||||
|
A |
N |
D |
A |
O |
D |
A2 |
|||
|
L |
N |
||||||||
|
а |
б |
в |
|||||||
|
Рис. 3 |
Первый способ решения. Проведём в пятиугольнике MFC1TN диагональ FT. Она ра-
зобьёт сечение на треугольник FC1T и четырёхугольник MFTN. Вычислим их площади по отдельности.
Найдем вначале площадь четырёхугольника MFTN. Поскольку MN || BD и BD лежит в плоскости BB1D1 , то MN || BB1D1 (по признаку параллельности прямой и плоскости). Так как секущая плоскость проходит через MN и пересекает плоскость BB1D1 по прямой TF, то TF ||MN (по теореме о линии пересечения). Далее, поскольку BD||MN и TF ||MN , то TF || BD. Следовательно, четырёхугольник MFTN – трапеция.
|
Из |
прямоугольного треугольника AMN по теореме Пифагора находим |
||||||
|
2a |
. Поскольку BF || DT , как отрезки, расположенные на боко- |
||||||
|
2 |
|||||||
|
MN |
AM2 AN2 |
||||||
|
3 |
вых рёбрах куба, то четырёхугольник BFTD – параллелограмм, а значит, TF BD a
 2 . Покажем, что трапеция MFTN – равнобедренная. Для этого рассмотрим вначале пря-
2 . Покажем, что трапеция MFTN – равнобедренная. Для этого рассмотрим вначале пря-
моугольный треугольник LDN. В нём ND a , LND 45 , следовательно, LD a . Да-
|
3 |
3 |
||||||||||||||||
|
лее, треугольники LDT и |
LCC |
подобны |
с коэффициентом k |
LD |
1 |
. Поэтому |
|||||||||||
|
1 |
LC 4 |
||||||||||||||||
|
CC1 |
|||||||||||||||||
|
DT |
a |
. Так как четырёхугольник BFTD – параллелограмм, то BF DT |
a |
, а зна- |
|||||||||||||
|
4 |
4 |
4 |
|||||||||||||||
|
чит, прямоугольные треугольники NDT и MBF равны по двум катетам. Поэтому, по тео- |
|||||||||||||||||
|
реме Пифагора, NT MF |
a |
2 |
a |
2 |
5a |
||||||||||||
|
. |
|||||||||||||||||
|
12 |
|||||||||||||||||
|
3 |
4 |
3

Далее находим длину h1 высоты этой равнобедренной трапеции MFTN. Опуская очевидные выкладки (читателю предлагается проделать их самостоятельно), получим
|
h |
a 17 |
. Отсюда S |
MFTN |
TF MN |
h |
a 2 2a 2 3 |
a 17 |
5a2 34 |
. |
||||||||||||||||||||||||||
|
12 |
2 |
2 |
12 |
72 |
|||||||||||||||||||||||||||||||
|
1 |
1 |
||||||||||||||||||||||||||||||||||
|
Решим теперь задачу вычисления площади треугольника FC1T . Найдём в нём длины |
|||||||||||||||||||||||||||||||||||
|
сторон FC1 и TC1 . Для этого рассмотрим прямоугольные треугольники FB1C1 |
и TD1C1. |
||||||||||||||||||||||||||||||||||
|
Они равны по двум катетам, поэтому по теореме Пифагора FC1 TC1 a |
2 |
3a |
2 |
5a |
|||||||||||||||||||||||||||||||
|
, |
|||||||||||||||||||||||||||||||||||
|
4 |
|||||||||||||||||||||||||||||||||||
|
4 |
т.е. треугольник FC1T – равнобедренный. Найдем длину h2 высоты этого треугольника. Опуская очевидные выкладки (читателю предлагается проделать их самостоятельно), по-
|
a 17 |
TF h |
1 |
a |
17 |
a2 34 |
||||||||||||||||||||||||||||||||||||
|
лучим h |
. Отсюда S |
FC T |
2 |
a |
2 |
. |
|||||||||||||||||||||||||||||||||||
|
2 |
4 |
2 |
2 |
4 |
8 |
||||||||||||||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||||||||||||||
|
Наконец, площадь всего сечения: |
|||||||||||||||||||||||||||||||||||||||||
|
5a2 |
a2 |
7a2 |
7a2 |
||||||||||||||||||||||||||||||||||||||
|
SMFC TN SMFTN |
S FC T |
34 |
34 |
34 |
. |
Ответ: |
34 |
. |
|||||||||||||||||||||||||||||||||
|
1 |
1 |
72 |
8 |
36 |
36 |
||||||||||||||||||||||||||||||||||||
Второй способ решения. Для нахождения площади сечения воспользуемся формулой (1). Ортогональной проекцией пятиугольника MFC1TN на плоскость ABC служит многоугольник MBCDN (см. рис. 3б). Найдём площадь MFC1TN . Очевидно, что SMBCDN SABCD S AMN . Треугольник AMN – прямоугольный. Длины его катетов AM и
|
AN, согласно условию задачи, равны |
2a |
. Поэтому SMBCDN a |
2 |
1 |
2a |
2 |
7a2 |
|||||||||||||||||||
|
. |
||||||||||||||||||||||||||
|
3 |
9 |
|||||||||||||||||||||||||
|
2 3 |
||||||||||||||||||||||||||
|
Далее, проведём в квадрате ABCD диагонали BD и AC. Равнобедренные прямоуголь- |
||||||||||||||||||||||||||
|
ные |
треугольники |
AMN |
и |
ABD |
подобны |
с коэффициентом |
k |
2 |
. Тогда |
|||||||||||||||||
|
3 |
||||||||||||||||||||||||||
|
AO |
2 |
AC |
AC |
, |
OC AC AO |
2a |
2 |
. Кроме того, поскольку MN || BD и BD AC , |
||||||||||||||||||
|
3 |
2 |
3 |
||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||
|
то MN OC. |
||||||||||||||||||||||||||
|
Соединим точки O и C1. Тогда OC1 |
– наклонная к плоскости ABC, OC – проекция на- |
|||||||||||||||||||||||||
|
клонной |
OC1 |
и MN OC. |
Следовательно, по |
теореме |
о |
трёх |
перпендикулярах, |
|||||||||||||||||||
|
MN OC1 . Значит, |
COC1 |
– линейный угол двугранного угла CMNC1 . |
Вычислим теперь косинус угла между плоскостью сечения и нижним основанием куба. Для этого рассмотрим прямоугольный треугольник CC1O . По теореме Пифагора
|
a 17 |
. Откуда cos |
OC |
2 |
2 |
. |
|||||||
|
OC |
OC2 CC2 |
|||||||||||
|
1 |
1 |
3 |
OC1 |
17 |
||||||||
Поскольку, согласно теореме о площади ортогональной проекции многоугольника,
|
SMFC TN |
S |
MBCDN |
, то окончательно получим: SMFC TN |
7a |
2 |
17 |
7a2 34 |
||||||||
|
. |
|||||||||||||||
|
cos |
|||||||||||||||
|
1 |
1 |
9 |
2 2 |
36 |
|||||||||||
Замечание. При решении задачи вторым способом для нахождения cos можно до-
строить секущую плоскость до её пересечения с продолжением ребра AA1 за точку A (см.
|
рис. 3в). Тогда cos |
SA BC D |
|
|
1 1 1 1 |
. |
|
|
SA MFC TN |
||
|
2 |
1 |
4
Пример 4. Дан куб ABCDA1B1C1D1 с ребром, равным a. Точка M – середина ребра AD,
точка N – середина ребра C1D1 . Найти площадь сечения куба плоскостью, проходящей через точки M, N и C.
Решение. Построим сечение куба плоскостью, проходящей через точки M, N и C. Соединим вначале точки M и C, поскольку они лежат в одной плоскости ABC. Затем соединим точки C и N, так как они лежат в одной плоскости DD1C1 (см. рис. 4). Прямые СN и
|
DD1 лежат в плоскости DD1C1 |
и не параллельны. Значит, они пересекаются в точке Q. |
||||
|
Точка Q принадлежит не только плоскости DD1C1, но и плоскости грани AA1D1 (как и |
|||||
|
точка M), |
поэтому, |
соединив M и Q, получим на ребре A1D1 принадлежащую сечению |
|||
|
точку P. В завершение построения соединим в верхней грани куба точки P и N. |
|||||
|
Q |
Отметим, что плоскости оснований куба парал- |
||||
|
лельны друг другу. Значит, по свойству параллель- |
|||||
|
ных плоскостей (если две параллельные плоскости |
|||||
|
пересечены третьей, то линии пересечения парал- |
|||||
|
B1 |
C1 |
лельны) MC|| PN . Далее, поскольку прямые MP и |
|||
|
CN пересекаются в точке Q, то стороны MP и CN че- |
|||||
|
A1 |
P |
N |
тырёхугольника MPNC не параллельны. Таким обра- |
||
|
D1 |
зом, сечением куба ABCDA1B1C1D1 является трапеция |
||||
|
MPNC. |
|||||
|
Для нахождения площади сечения воспользуемся |
|||||
|
формулой (1). Построим вначале линейный угол дву- |
|||||
|
BO |
C |
гранного угла DMCQ. Для этого в прямоугольном |
|||
|
треугольнике MCD опустим перпендикуляр DO к ги- |
|||||
|
N1 |
потенузе MC. Соединим точки O и Q. Тогда QO – на- |
||||
|
A |
M |
P1 D |
клонная к плоскости ABC, DO – проекция наклонной |
||
|
QO и MC DO. |
Следовательно, по теореме о трёх |
||||
|
Рис. 4 |
перпендикулярах, |
MC QO. Значит, QOD – |
|||
|
линейный угол двугранного угла DMCQ. |
Вычислим теперь косинус угла между плоскостью сечения и нижним основанием куба. Для этого рассмотрим вначале прямоугольный треугольник MCD. По теореме Пифа-
|
a2 |
|||||||||||||||||||||||||||
|
a 5 |
. Для нахождения высоты DO выразим пло- |
||||||||||||||||||||||||||
|
гора MC |
MD2 DC2 |
a2 |
|||||||||||||||||||||||||
|
щадь S MCD |
двумя способами: |
4 |
2 |
||||||||||||||||||||||||
|
MD DC |
a2 |
MC DO |
a |
||||||||||||||||||||||||
|
S MCD |
, S MCD |
5 |
DO. |
||||||||||||||||||||||||
|
2 |
4 |
||||||||||||||||||||||||||
|
2 |
4 |
||||||||||||||||||||||||||
|
a2 |
a |
a |
|||||||||||||||||||||||||
|
5 |
DO. Отсюда DO |
||||||||||||||||||||||||||
|
Тогда, приравняв их, получим |
. |
||||||||||||||||||||||||||
|
4 |
4 |
||||||||||||||||||||||||||
|
5 |
|||||||||||||||||||||||||||
Далее, рассмотрим прямоугольные треугольники CDQ и ND1Q. У этих треугольников острый угол при вершине Q – общий. Значит, они подобны. Поскольку, согласно условию
|
задачи, точка N – |
середина ребра C1D1, то коэффициент подобия треугольников CDQ и |
|||||||||||||||||||
|
ND1Q равен 2. Отсюда, очевидно, что DQ 2a. |
||||||||||||||||||||
|
Рассмотрим, |
наконец, |
прямоугольный треугольник QOD. По теореме Пифагора |
||||||||||||||||||
|
a2 |
a |
DO |
1 |
|||||||||||||||||
|
2 |
21 |
|||||||||||||||||||
|
QO DQ |
2 |
DO |
2 |
4a |
. Откуда cos |
. |
||||||||||||||
|
5 |
QO |
|||||||||||||||||||
|
5 |
21 |
|||||||||||||||||||
Построим теперь четырёхугольник MP1N1C, являющийся ортогональной проекцией трапеции MPNC на плоскость ABC. Так как PN лежит в плоскости, построенной на парал-
5
|
лельных прямых PP1 и NN1, |
и параллельна плоскости ABC, |
то линия пересечения |
P1N1 |
||||||||||||||||||||||||||||
|
плоскостей ABC и PNN1 |
параллельна PN (по теореме о линии пересечения). Поскольку |
||||||||||||||||||||||||||||||
|
P1N1 || PN и MC|| PN , то P1N1 ||MC, а значит, четырёхугольник MP1N1C – трапеция. |
|||||||||||||||||||||||||||||||
|
Найдём площадь трапеции MP1N1C. Очевидно, что SMPN C S |
MCD |
S PN D . Прямо- |
|||||||||||||||||||||||||||||
|
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||||
|
угольные треугольники MCD и P1N1D подобны, так как P1N1D MCD (как соответст- |
|||||||||||||||||||||||||||||||
|
венные). Точка |
N1 – середина ребра CD, значит, |
коэффициент подобия треугольников |
|||||||||||||||||||||||||||||
|
MCD и PN |
D равен 2. Поэтому S |
MPN C |
S |
MCD |
S |
MCD |
a2 |
a2 |
3a2 |
. |
|||||||||||||||||||||
|
1 1 |
4 |
4 |
16 |
16 |
|||||||||||||||||||||||||||
|
1 |
1 |
||||||||||||||||||||||||||||||
|
Согласно |
теореме |
о |
площади |
ортогональной |
проекции |
многоугольника, |
|||||||||||||||||||||||||
|
SMP1N1C |
3a2 |
||||||||||||||||||||||||||||||
|
SMPNC |
, откуда окончательно получим: SMPNC |
21 |
. |
||||||||||||||||||||||||||||
|
cos |
16 |
||||||||||||||||||||||||||||||
|
3a2 |
|||||||||||||||||||||||||||||||
|
Ответ: |
21 |
. |
|||||||||||||||||||||||||||||
16
3. Применение теоремы о площади ортогональной проекции многоугольника при вычислении угла между плоскостями
Кроме рассмотренного основного применения теоремы о площади ортогональной проекции многоугольника её можно также использовать при вычислении угла между плоскостью сечения и плоскостью какой-либо грани многогранника (обычно в качестве такой грани выступает основание пирамиды или призмы). Так поступают в случаях, когда нахождение Sпр и Sсечения является более простой задачей, чем непосредственное вычисление двугранного угла , сопряжённое с построением на чертеже его линейного угла.
B1
A1 D1
D1
B

A D
Рис. 5
Из формулы о
|
C1 |
Пример 5. В кубе |
ABCDA1B1C1D1 найти угол между |
|||||||||||
|
плоскостью грани AA1B1B и плоскостью BC1D. |
|||||||||||||
|
Решение. Пусть ребро куба равно a. Ортогональной |
|||||||||||||
|
проекцией треугольника BC1D является треугольник AB1B |
|||||||||||||
|
a2 |
|||||||||||||
|
C |
(см. рис. 5), площадь |
которого равна |
. |
Поскольку |
|||||||||
|
2 |
|||||||||||||
|
BD BC1 |
C1A a |
(как диагонали |
граней |
куба), то |
|||||||||
|
2 |
|||||||||||||
|
a2 . |
|||||||||||||
|
S BC D |
3 |
||||||||||||
|
2 |
|||||||||||||
|
1 |
|||||||||||||
площади ортогональной проекции многоугольника получим:
|
S AB B |
3 |
. Отсюда arccos |
3 |
. |
Ответ: arccos |
3 |
. |
||||||||||||
|
1 |
|||||||||||||||||||
|
S BC D |
3 |
3 |
3 |
||||||||||||||||
|
1 |
|||||||||||||||||||
|
B1 |
P |
C1 |
Пример 6. В кубе |
ABCDA1B1C1D1 через его вершины |
|||||||||||||||
|
A , D и точку M, расположенную на ребре CC |
так, что |
||||||||||||||||||
|
1 |
1 |
||||||||||||||||||
|
D1 |
M |
CM :MC1 2:1, проведено сечение. Найти угол наклона |
|||||||||||||||||
|
Q |
секущей плоскости к плоскости основания ABCD. |
||||||||||||||||||
|
K |
Решение. Построим сечение куба плоскостью, прохо- |
||||||||||||||||||
|
B |
L |
C |
дящей через точки A1, D и M. Соединим вначале точки A1 |
||||||||||||||||
|
и D, поскольку они лежат в одной плоскости DD A . Затем |
|||||||||||||||||||
|
1 |
1 |
Dсоединим точки D и M, так как они лежат в одной плоскости DD1C1 (см. рис. 6). Противоположные боковые грани
|
Рис. 6 |
DD1A1 |
и CC1B1 в кубе параллельны. Поэтому секущая |
6

плоскость, согласно свойству параллельных плоскостей (если две параллельные плоскости пересечены третьей, то линии пересечения параллельны) будет пересекать грань CC1B1 по прямой MP так, что MP|| A1D . Наконец, соединим точки A1 и P, так как они лежат в одной плоскости A1B1C1. Поскольку A1P и DM не параллельны, то четырёхуголь-
ник A1PMD, являющийся сечением куба, – трапеция.
Ортогональной проекцией трапеции A1PMD плоскости основания ABCD является прямоугольная трапеция ALCD. Для определения угла наклона секущей плоскости к
плоскости основания ABCD воспользуемся формулой cos SALCD . Для этого найдем
SA1PMD
площади указанных трапеций.
|
Пусть ребро куба равно a. Тогда, согласно условию задачи, MC a . Кроме того, |
|
|
1 |
3 |
очевидно, что A1D a
 2. Поскольку MP|| A1D и DD1 ||MC1, то A1DD1 PMC1 (как углы с соответственно сонаправленными сторонами). Поэтому прямоугольные треуголь-
2. Поскольку MP|| A1D и DD1 ||MC1, то A1DD1 PMC1 (как углы с соответственно сонаправленными сторонами). Поэтому прямоугольные треуголь-
|
ники A DD и PMC подобны с коэффициентом k |
1 |
. Следовательно, MP |
A1D |
a 2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
1 |
3 |
3 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A1D1 |
a |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
и PC |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
3 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Далее, |
так как |
A B DC a, B P CM |
, |
то |
прямоугольные |
треугольники |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
1 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A1B1P |
DCM |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
и |
равны |
по |
двум |
катетам. |
Поэтому |
по |
теореме |
Пифагора |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4a2 |
a |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A P DM a2 |
13 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
9 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Следовательно, трапеция A1PMD равнобедренная. Найдём её высоту. Для этого опус- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
тим из |
точек P |
и |
M |
перпендикуляры |
PQ и |
MK |
на |
основание A1D. Тогда |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A1D MP |
a |
. Отсюда по теореме Пифагора из прямоугольного треуголь- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AQ DK |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
13a2 |
2a2 |
a |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
11 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ника A PQ высота трапеции A PMD равна: |
PQ |
A P2 |
AQ2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
1 |
1 |
9 |
9 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A D MP |
2a2 |
22 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Таким образом, площадь сечения: SAPMD |
1 |
PQ |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
9 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
В прямоугольной трапеции ALCD основания равны AD a |
и LC PC |
, |
а высота |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AD LC |
2a2 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
DC a . Тогда её площадь: |
SALCD |
DC |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подставляя полученные значения площадей в формулу, находим |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
S |
2a |
2 |
2a2 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
cos |
ALCD |
: |
22 |
22 |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
SAPMD |
3 |
9 |
22 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
Ответ: arccos |
3 |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Следовательно, arccos |
22 |
. |
22 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
22 |
22 |
Пример 7. Плоскость пересекает прямоугольный параллелепипед с квадратным основанием по ромбу с острым углом . Под каким углом эта плоскость пересекает боковые рёбра параллелепипеда?
7
Решение. Без ограничения общности рассуждений будем считать, что секущая плоскость проходит через вершину A нижнего основания параллелепипеда, пересекая его бо-
|
ковые рёбра BB1, CC1 |
и DD1 |
в точках M, N и P соответственно (см. рис. 7). |
|||
|
B1 |
C1 |
Рассмотрим прямоугольные треугольники AMB и |
|||
|
D1 |
N |
APD. В них AM AP , т.к., согласно условию, AMNP – |
|||
|
A1 |
ромб. Кроме того, AB AD как стороны основания |
||||
|
x |
параллелепипеда ABCD, являющегося квадратом. Сле- |
||||
|
x |
довательно, AMB APD по гипотенузе и катету, а |
||||
|
M |
значит, MB PD. |
||||
|
O |
Рассмотрим теперь четырёхугольник BMPD. В нём |
||||
|
x |
P |
противоположные стороны MB и PD параллельны и |
|||
|
x B |
a |
равны, значит, BMPD – параллелограмм (отметим до- |
|||
|
C |
полнительно, что BMPD – прямоугольник). Отсюда |
||||
|
a |
a |
MP|| BD и MP BD. |
|||
|
A |
a |
D |
Пусть сторона ромба AMNP равна x, а ребро осно- |
||
|
Рис. 7 |
вания параллелепипеда равно a. Тогда SAMNP x2 sin , |
SABCD a2 . Поскольку MP BD a
 2, то из прямо-
2, то из прямо-
|
угольного треугольника AOP имеем: sin |
OP |
a 2 |
, или a x |
sin |
. |
|||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||
|
2 |
AP |
2x |
2 |
|||||||||||||||||||||||||||||
|
Вычислим косинус угла между секущей плоскостью и основанием: |
||||||||||||||||||||||||||||||||
|
SABCD |
a2 |
2x2 sin2 |
||||||||||||||||||||||||||||||
|
cos |
2 |
tg |
. |
|||||||||||||||||||||||||||||
|
SAMNP |
x2 sin |
|||||||||||||||||||||||||||||||
|
Обозначим через угол, |
x2 sin |
2 |
||||||||||||||||||||||||||||||
|
под которым секущая плоскость пересекает боковые рёбра |
||||||||||||||||||||||||||||||||
|
параллелепипеда. Поскольку |
, то |
cos cos |
sin . Значит, |
sin tg |
. |
|||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||
|
Отсюда arcsin tg |
. |
|||||||||||||||||||||||||||||||
2
|
Ответ: arcsin tg |
. |
||||||||
|
2 |
|||||||||
|
Пример 8. В кубе ABCDA1B1C1D1 с ребром, равным a, через точки M, P и N на рёбрах |
|||||||||
|
BB , CC и DD соответственно, такие, что BM |
3a |
, CP |
2a |
и DN |
a |
, проведена се- |
|||
|
1 |
1 |
1 |
4 |
3 |
4 |
||||
кущая плоскость. Найти угол между плоскостью сечения и плоскостью основания куба.
Решение. Построим сечение куба плоскостью, проходящей через точки M, P и N. Соединим вначале точки M и P, поскольку они лежат в одной плоскости BB1C1 . Затем соединим точки P и N, т.к. они лежат в одной плоскости
DD1C1 (см. рис. 8).
Противоположные боковые грани AA1D1 и BB1C1 в кубе параллельны. Поэтому секущая плоскость, согласно свойству параллельных плоскостей (если две параллельные плоскости пересечены третьей, то линии пересечения параллельны) будет пересекать грань AA1D1 по прямой NQ так, что
NQ|| MP.
8

Соединим точки M и Q, т.к. они лежат в одной плоскости AA1B1. Тогда MQ|| NP по
|
тому же свойству параллельных плоскостей AA1B1 |
и |
CC1D1 . Таким образом, |
сечение |
||||||||||||||||||||||||||||||||||||||||||||||||
|
представляет собой параллелограмм MPNQ. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вычислим площадь MPNQ и, поскольку квадрат ABCD – ортогональная проекция |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
MPNQ, определим косинус угла между плоскостью сечения и плоскостью ABC. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Найдём стороны треугольника MNP. Используя теорему Пифагора, получим: |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
из прямоугольного треугольника MLP (ML CC1 ) |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
a2 |
a2 |
a |
, |
||||||||||||||||||||||||||||||||||||||||||||||||
|
145 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
MP (LC PC)2 MC2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
144 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
из прямоугольного треугольника NPS (NS CC1) |
12 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
NP |
25a2 |
a2 |
13a |
, |
|||||||||||||||||||||||||||||||||||||||||||||||
|
(PC SC)2 NS2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
из прямоугольного треугольника MNK (KN BB1) |
144 |
12 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
MN |
a2 |
2a2 |
3a |
. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
(BM BK)2 KN2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Полупериметр треугольника MNP равен p |
a( |
31) |
. Используя формулу Герона, |
||||||||||||||||||||||||||||||||||||||||||||||||
|
145 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
24 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
a2 |
a2 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
найдём его площадь: |
SMNP |
170 |
. Следовательно, |
SMPNQ 2SMNP |
170 |
. Из фор- |
|||||||||||||||||||||||||||||||||||||||||||||
|
24 |
12 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
SABCD |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
мулы для |
площади |
ортогональной |
проекции получим: cos |
12 |
. Отсюда |
||||||||||||||||||||||||||||||||||||||||||||||
|
SMPNQ |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
170 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
arccos |
6 |
170 |
. |
Ответ: arccos |
6 |
170 |
. |
||||||||||||||||||||||||||||||||||||||||||||
|
85 |
85 |
||||||||||||||||||||||||||||||||||||||||||||||||||
4. Применениетеоремы о площади ортогональной проекции многоугольника при вычислении площади боковой поверхности пирамиды
Ещё одной известной задачей, при решении которой применяется теорема о площади ортогональной проекции многоугольника, является задача вычисления площади Sбок бо-
ковой поверхности пирамиды, у которой все боковые грани одинаково наклонены к плоскости её основания (под углом ), или вершина пирамиды лежит на перпендикуляре, восставленном из центра вписанной в её основание окружности. Тогда
|
Sбок |
Sосн |
. |
(2) |
|
|
cos |
Пример 9. Стороны основания треугольной пирамиды равны 6 см, 10 см и 14 см. Каждый двугранный угол при её основании равен 30°. Найти площадь боковой поверхности пирамиды.
Решение. Для нахождения площади сечения воспользуемся формулой (2). Найдём вначале площадь основания треугольной пирамиды, воспользовавшись формулой Герона. Поскольку полупериметр треугольника в основании равен 15 см, то
Sосн 
 15 (15 6) (15 10) (15 14) 15
15 (15 6) (15 10) (15 14) 15
 3 (см2).
3 (см2).
|
Тогда Sбок |
Sосн |
3 |
2 |
||||||
|
15 3: |
30 |
||||||||
|
(см ). |
|||||||||
|
cos30 |
2 |
||||||||
Ответ: 30 см2.
9
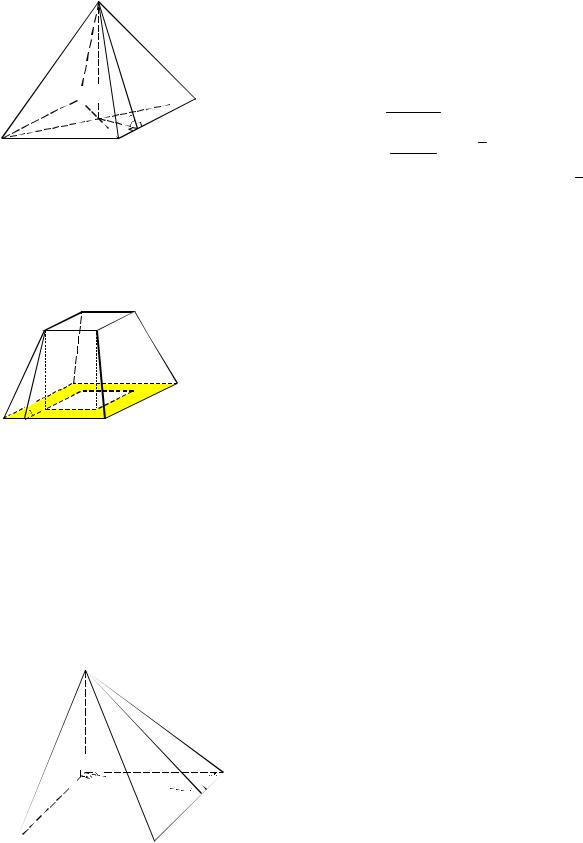
Пример 10. Боковые грани пирамиды, в основании которой лежит ромб, наклонены к плоскости основания под углом 30°. Диагонали ромба равны 10 см и 24 см. Найти площадь боковой поверхности пирамиды.
Решение. Для нахождения площади сечения воспользуемся формулой (2). Поскольку боковые грани пирамиды SABCD наклонены к основанию ABCD под одинаковым углом, то её вершина S проектируется в центр вписанной в ромб окружности, т. е. в точку O пересечения его диагоналей (см. рис. 9). Тогда
SABCD AC BD 120 (см2). 2
Следовательно, Sбок SABCD 80
 3 (см2). cos30
3 (см2). cos30
Ответ: 80
 3 см2.
3 см2.
Пример 11. В правильной усечённой четырёхугольной пирамиде стороны нижнего и верхнего оснований равны соответственно a и b (a b). Найти площадь полной поверхности усечённой пирамиды, если её боковые грани наклонены к плоскости основания под углом .
|
b |
Решение. Поскольку основаниями правильной усе- |
||||||||||||
|
чённой четырёхугольной пирамиды являются квадраты со |
|||||||||||||
|
сторонами a и b, то сумма их площадей равна |
a2 b2 . |
||||||||||||
|
Очевидно, что ортогональная проекция боковой поверхно- |
|||||||||||||
|
сти усечённой пирамиды на плоскость нижнего основания |
|||||||||||||
|
a |
представляет собой квадрат со стороной a, из которого |
||||||||||||
|
«вырезан» квадрат со стороной b. При этом стороны «вы- |
|||||||||||||
|
Рис. 10 |
резанного» квадрата параллельны сторонам нижнего осно- |
||||||||||||
|
вания пирамиды (см. рис. 10). Так как боковые грани усе- |
|||||||||||||
|
чённой пирамиды наклонены к плоскости основания под |
|||||||||||||
|
одинаковым углом , то площадь её боковой поверхности равна: Sбок |
Sпр |
a2 |
b2 |
||||||||||
|
. |
|||||||||||||
|
cos |
|||||||||||||
|
cos |
|||||||||||||
|
Таким образом, S |
полн a |
2 |
b |
2 |
a2 b2 |
Ответ: a |
2 |
b |
2 |
a2 b2 |
|||
|
. |
. |
||||||||||||
|
cos |
cos |
Пример 12. Основанием пирамиды является ромб. Две боковые грани перпендикулярны к плоскости основания и образуют двугранный угол в 120°, а две другие боковые грани наклонены к плоскости основания под углом 30°. Найти площадь поверхности пирамиды, если её высота равна 12.
Решение. Площадь полной поверхности пирамиды равна сумме площадей боковых граней и основания, т. е.
Sполн SASB SBSC SASD SDSC SABCD .
Положим, что сторона ромба ABCD равна a. C Пусть боковые грани ASB и BSC пирамиды
SABCD перпендикулярны к плоскости основания ABCD (см. рис. 11). Тогда боковое ребро SB пирамиды перпендикулярно к плоскости ромба и равно высоте, а боковые грани ASB и BSC пирамиды являются равными прямоугольными треугольниками
10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Вы уже изучили свойства равностороннего треугольника и квадрата. Каждая из этих фигур обладает тем свойством, что у них все углы равны и все стороны равны. Указанные геометрические фигуры служат примерами правильных многоугольников, свойства которых и рассматриваются в данном параграфе.
Определение правильного многоугольника
Определение. Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
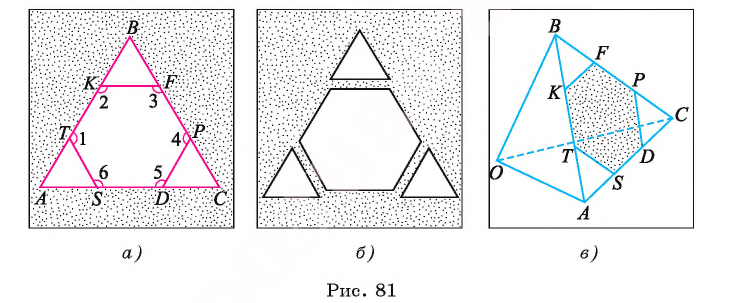
Рассмотрим пример. Пусть ABC — равносторонний треугольник;. Разделим каждую его сторону на три равные части, как показано на рисунке 81, а. Каждый из треугольников ATS, KBF и DPC является равносторонним. Отсюда следует, что 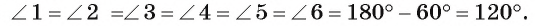
Модель этого правильного многоугольника получится, если от листа бумаги, имеющего форму равностороннего треугольника, отрезать равные части, имеющие форму равносторонних и равных между собой треугольников, как показано на рисунке 81, б.
Если треугольник АБС является гранью тетраэдра ВОАС (тетраэдр — треугольная пирамида, у которой все четыре грани — равные равносторонние треугольники), а каждая пара точек Т, К, F, Р и D, S делит соответственно ребра АВ, ВС и АС на три равные части, то TKFPDS — правильный шестиугольник, лежащий на грани ABC (рис. 81, в).
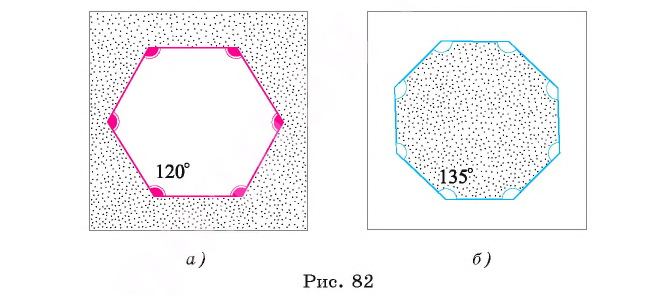
Ранее, в § 1 главы 1 учебного пособия «Геометрия, 8», была доказана теорема о том, что сумма градусных мер углов любого выпуклого n-угольника равна 180°(n – 2). Из доказанной теоремы и определения правильного n-угольника следует, что градусную меру каждого его угла можно найти по формуле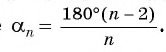 Например, для правильного шести
Например, для правильного шести 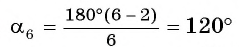 (рис. 82, о), а для правильного восьмиугольника
(рис. 82, о), а для правильного восьмиугольника 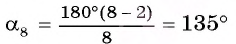 (рис. 82, б).
(рис. 82, б).
Окружность, описанная около правильного многоугольника
Вы знаете, что около правильного треугольника и правильного четырехугольника можно описать окружность. Теперь изучим вопрос о существовании окружности, описанной около правильного многоугольника.
Определение. Окружность называется описанной около многоугольника, если все его вершины лежат на этой окружности. При этом многоугольник называется вписанным в окружность.
Оказывается, что около любого правильного многоугольника можно описать окружность. Докажем следующую теорему.
Теорема 1 (об окружности, описанной около правильного многоугольника). Около любого правильного многоугольника можно описать единственную окружность.
Доказательство.
I. Докажем, существование окружности.
1) Пусть 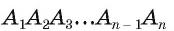 — правильный многоугольник. Докажем, что существует точка, равноудаленная от всех его вершин. Пусть точка О — точка пересечения биссектрис углов
— правильный многоугольник. Докажем, что существует точка, равноудаленная от всех его вершин. Пусть точка О — точка пересечения биссектрис углов 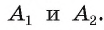 Соединим точку О отрезками со всеми вершинами многоугольника и докажем, что
Соединим точку О отрезками со всеми вершинами многоугольника и докажем, что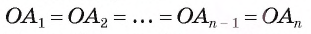 (рис. 83).
(рис. 83).
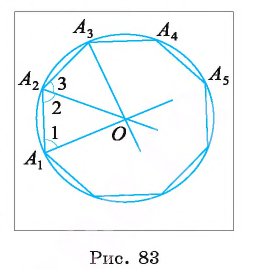
2) Так как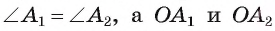 — биссектрисы, то
— биссектрисы, то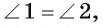 т. е. треугольник
т. е. треугольник 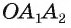 — равнобедренный, а значит,
— равнобедренный, а значит,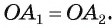
3) Заметим, что треугольник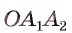 равен треугольнику
равен треугольнику 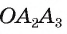 по двум сторонам и углу между ними (
по двум сторонам и углу между ними (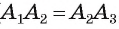 ,сторона
,сторона 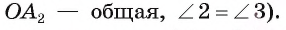 . Из равенства этих треугольников следует, что
. Из равенства этих треугольников следует, что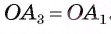 Так же можно доказать, что
Так же можно доказать, что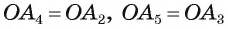 и т. д.
и т. д.
4) Таким образом,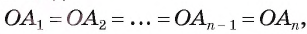 т. е. точка О равноудалена от вершин многоугольника. Следовательно, окружность со с центром в точке О и радиуса ОА, является описанной около многоугольника. Из доказательства следует, что центром, окружности, описанной около правильного многоугольника, является точка пересечения биссектрис углов этого многоугольника.
т. е. точка О равноудалена от вершин многоугольника. Следовательно, окружность со с центром в точке О и радиуса ОА, является описанной около многоугольника. Из доказательства следует, что центром, окружности, описанной около правильного многоугольника, является точка пересечения биссектрис углов этого многоугольника.
II. Докажем, что описанная окружность единственная.
Пусть существует еще одна окружность со,, которая описана около правильного многоугольника Тогда эта окружность является описанной, например, около треугольника
Тогда эта окружность является описанной, например, около треугольника Но около треугольника
Но около треугольника  можно описать единственную окружность, значит, окружности со и со, совпадают, т. е. около многоугольника
можно описать единственную окружность, значит, окружности со и со, совпадают, т. е. около многоугольника  можно описать единственную окружность.
можно описать единственную окружность.
Теорема доказана.
Окружность, вписанная в правильный многоугольник
Известно, что в любой правильный треугольник можно вписать окружность. Рассмотрим вопрос о существовании окружности, вписанной в правильный многоугольник.
Определение. Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности. При этом многоугольник называется описанным около окружности.
Докажем, что в любой правильный многоугольник можно вписать окружность.
Теорема 2 (об окружности, вписанной в правильный многоугольник). В любой правильный многоугольник можно вписать единственную окружность.
I. Докажем существование окружности.
1) Пусть  — правильный многоугольник. Докажем, что существует точка, равноудаленная от прямых, содержащих стороны многоугольника (рис. 84).
— правильный многоугольник. Докажем, что существует точка, равноудаленная от прямых, содержащих стороны многоугольника (рис. 84).
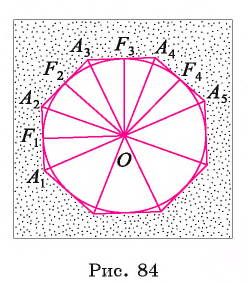
2) Пусть точка О — центр описанной около многоугольника окружности. Теперь проведем высоты
 соответственно треугольников
соответственно треугольников Как было доказано в предыдущей теореме, эти треугольники равны между собой, следовательно, равны их высоты, т. е.
Как было доказано в предыдущей теореме, эти треугольники равны между собой, следовательно, равны их высоты, т. е.
3) Таким образом, окружность  с центром в точке О радиуса
с центром в точке О радиуса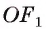 проходит через точки
проходит через точки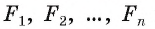 и касается сторон многоугольника в этих точках, т. е. эта окружность вписана в правильный многоугольник
и касается сторон многоугольника в этих точках, т. е. эта окружность вписана в правильный многоугольник 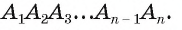
Заметим также, что центр О вписанной в правильный многоугольник окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
Подчеркнем, что для правильного многоугольника центр вписанной окружности совпадает с центром, описанной окружности.
II. Докажем, что вписанная окружность единственная.
Предположим, что существует еще одна окружность  вписанная в правильный многоугольник
вписанная в правильный многоугольник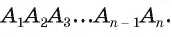 Тогда центр Ох этой окружности равноудален от сторон многоугольника, т. е. точка О, лежит на каждой из биссектрис углов многоугольника, а значит, совпадает с точкой О пересечения этих биссектрис. Радиус этой окружности равен расстоянию от точки О до сторон многоугольника, т. е. он равен
Тогда центр Ох этой окружности равноудален от сторон многоугольника, т. е. точка О, лежит на каждой из биссектрис углов многоугольника, а значит, совпадает с точкой О пересечения этих биссектрис. Радиус этой окружности равен расстоянию от точки О до сторон многоугольника, т. е. он равен Следовательно, окружности
Следовательно, окружности  совпадают.
совпадают.
Теорема доказана.
Центром, правильного многоугольника называется центр его вписанной и описанной окружностей.
Выражение элементов n-угольника через радиус вписанной или описанной окружностей
Пусть S — площадь правильного n-угольника, 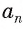 — длина его стороны, Р — периметр, а г и R — радиусы вписанной и описанной окружностей соответственно.
— длина его стороны, Р — периметр, а г и R — радиусы вписанной и описанной окружностей соответственно.
1) Площадь S правильного n-уголъника, описанного около окружности, можно найти, зная периметр Р и радиус г вписанной окружности, по формуле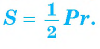
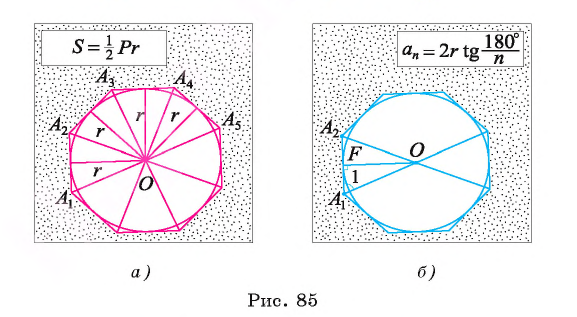
Соединим центр О правильного многоугольника с его вершинами (рис. 85, а). Тогда многоугольник разбивается на n равных треугольников, площадь каждого из которых равна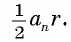 Следовательно,
Следовательно,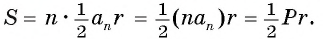
Что и требовалось доказать.
2) Длину стороны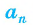 правильного n-угольника можно найти, зная радиус г вписанной окружности, по формуле
правильного n-угольника можно найти, зная радиус г вписанной окружности, по формуле 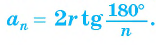
Соединим центр многоугольника с вершинами  и проведем высоту OF равнобедренного треугольника
и проведем высоту OF равнобедренного треугольника  (рис. 85, б). Так как многоугольник правильный, то
(рис. 85, б). Так как многоугольник правильный, то 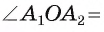
 в равнобедренном треугольнике
в равнобедренном треугольнике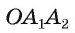 высота OF, проведенная к основанию, является биссектрисой, следовательно,
высота OF, проведенная к основанию, является биссектрисой, следовательно,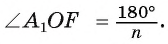 Таким образом,
Таким образом,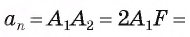
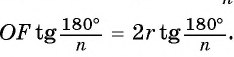
Что и требовалось доказать.
Так как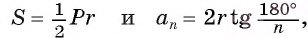 , то площадь S =
, то площадь S =
3) Длину стороны аn правильного n-угольника можно найти, зная радиус R описанной окружности, по формуле 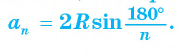
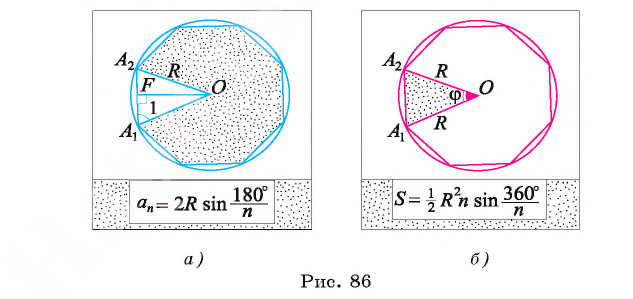
Пусть OF — высота равнобедренного треугольника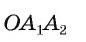 (рис. 86, а). Тогда
(рис. 86, а). Тогда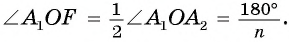 В прямоугольном треугольнике
В прямоугольном треугольнике 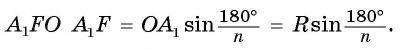 Таким образом,
Таким образом, 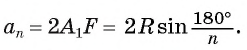
Что и требовалось доказать.
Для правильного треугольника (n = 3), квадрата (n = 4) и правильного шестиугольника, (n = 6) получим соответственно формулы: 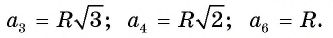
4) Площадь S правильного п-угольника можно найти, зная радиус R описанной окружности, по формуле 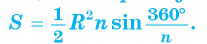
Соединим вершины правильного /i-угольника с его центром (рис 86, б). Тогда многоугольник разобьется на п равных треугольников. Следовательно, 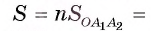
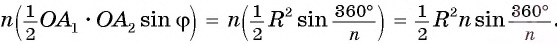
Что и требовалось доказать.
5) Радиус г вписанной окружности можно найти, зная радиус R описанной окружности, по формуле 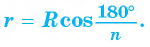
В прямоугольном треугольнике 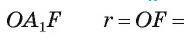
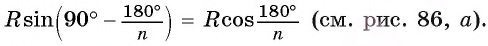
Что и требовалось доказать.
Построение правильных многоугольников
Вопрос о построении правильного треугольника уже рассматривался ранее. Покажем, каким образом можно с помощью циркуля и линейки построить правильный треугольник, вписанный в окружность.
Пример №1
Постройте правильный треугольник, вписанный в данную окружность.
Поиск решения.
Пусть правильный треугольник ABC вписан в окружность с центром в точке О. Проведем диаметр BF этой окружности, обозначим буквой Т точку пересечения этого диаметра со стороной АС. Тогда положение точки Т на отрезке OF характеризуется равенством ОТ = TF; т. к. центр равностороннего треугольника есть точка пересечения медиан, то 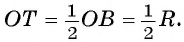 Кроме того,
Кроме того,  Теперь можем осуществить построение (рис. 87, а).
Теперь можем осуществить построение (рис. 87, а).
Построение.
1) Проводим диаметр BF окружности и строим точку Т — середину отрезка OF (рис. 87, б).
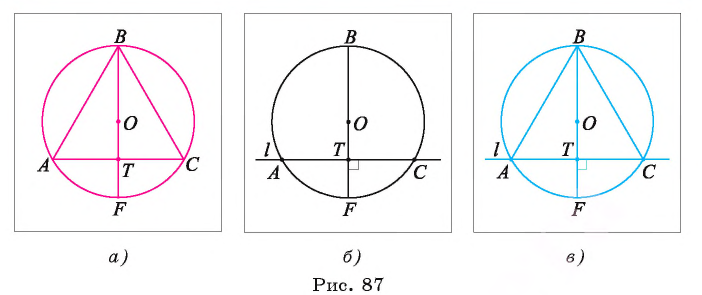
Строим прямую l, которая проходит через точку Т и перпендикулярна диаметру BF (рис. 87, б).
3) Отметим точки А и С пересечения прямой l с окружностью.
4) Строим отрезки ВА и ВС (рис. 87, в). Треугольник ABC — искомый.
Докажите самостоятельно, что построенный треугольник — правильный.
Пример №2
Постройте правильный шестиугольник, сторона которого равна данному отрезку а.
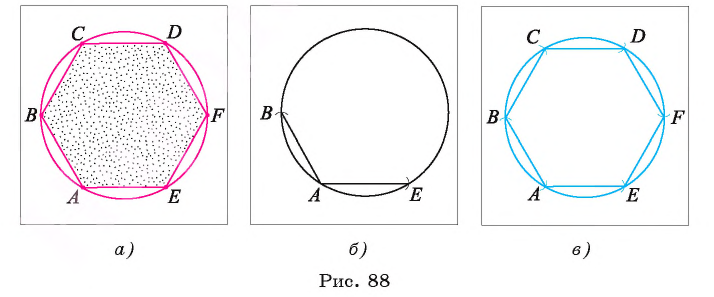
Поиск решения.
Пусть ABCDFE — правильный шестиугольник, сторона. которого равна а. Рассмотрим, описанную около этого шестиугольника окружность. Известно, что радиус окружности, описанной около правильного шестиугольника, равен его стороне, т. е. R = АВ = ВС = CD = DF = FE = ЕА = a.(рис. 88). Этим можем воспользоваться для построения шестиугольника.
Построение.
1) Строим окружность 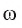 с центром О и радиуса а.
с центром О и радиуса а.
2) Выбираем на этой окружности произвольную точку А и строим окружность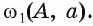 Отметим точки В и Е пересечения окружности
Отметим точки В и Е пересечения окружности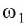 , с окружностью
, с окружностью 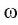 (рис. 88, б).
(рис. 88, б).
3) Далее строим точку С, которая является одной из точек пересечения окружности и окружности
и окружности  Аналогично строим точки D и F. Шестиугольник ABCDFE — искомый (рис. 88, в).
Аналогично строим точки D и F. Шестиугольник ABCDFE — искомый (рис. 88, в).
Заметим, что результат задачи 1 позволяет построить правильный шестиугольник, если построен правильный треугольник.
Понятие длины окружности
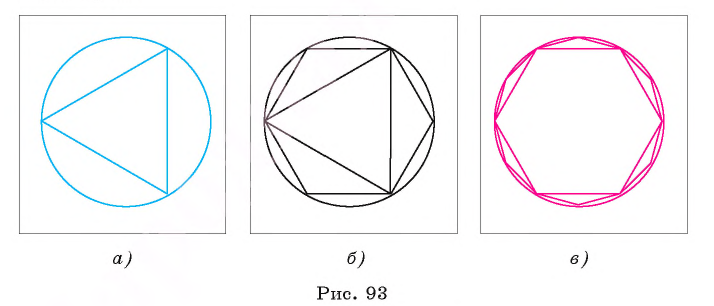
Рассмотрим вопрос о вычислении длины окружности. Пусть в окружность вписан правильный n-угольник. Если число n сторон правильного « угольника, вписанного в окружность, неограниченно возрастает, то геометрическая фигура, образованная его сторонами, все меньше и меньше отличается от окружности (рис. 93, а, б, в). В вузовском курсе математического анализа устанавливается, что существует число, к которому стремятся периметры Р„ правильных n-угольников, вписанных в окружность, при неограниченном возрастании числа их сторон. Это число называется длиной окружности. Таким образом, за длину окружности принимается число, к которому стремятся периметры вписанных в окружность правильных n-угольников при неограниченном увеличении числа их сторон.
Длина окружности зависит от ее радиуса, окружность большего радиуса имеет большую длину. Вместе с тем можно доказать, что отношение длины окружности к ее диаметру есть число постоянное.
2. Теорема об отношении длины окружности к ее диаметру. Докажем теорему, которая характеризует отношение длины окружности к ее диаметру.
Теорема (об отношении длины окружности к ее диаметру).
Отношение длины окружности к ее диаметру есть число постоянное для всех окружностей.
Дано: 
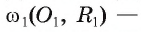 окружности,
окружности, 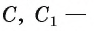 соответственно длины этих окружностей. Доказать:
соответственно длины этих окружностей. Доказать: 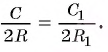
Доказательство.
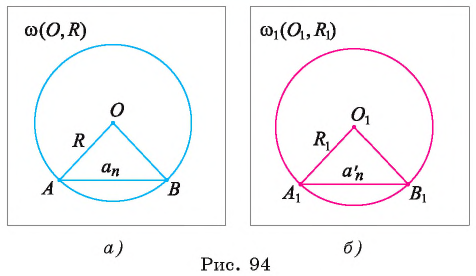
1) Впишем в каждую из окружностей правильные n-угольники. Пусть длины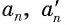 — стороны этих многоугольников,
— стороны этих многоугольников,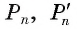 — соответственно их периметры (рис. 94, а, б).
— соответственно их периметры (рис. 94, а, б).
2) Теперь воспользуемся формулой, которой выражается длина стороны правильного п-угольника через радиус описанной окружности. Учитывая эту формулу (глава 3, § 1, п. 3), можем записать равенства 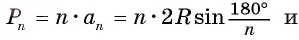 .
.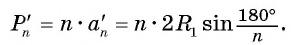 Следовательно, верно равенство
Следовательно, верно равенство 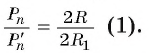
3) Это равенство верно при любом значении n. Будем неограниченно увеличивать число n, тогда периметр 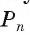 первого многоугольника стремится к длине С первой окружности, а периметр
первого многоугольника стремится к длине С первой окружности, а периметр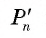 второго многоугольника стремится к длине
второго многоугольника стремится к длине 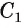 второй окружности, т. е.
второй окружности, т. е. 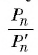 стремится к
стремится к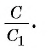
4) Таким образом, 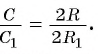 Отсюда следует, что
Отсюда следует, что 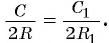
Значит, отношение длины окружности к ее диаметру одно и то же для всех окружностей.
Теорема доказана.
Число, равное отношению длины окружности к ее диаметру, обозначается строчной греческой буквой 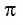 (читается «пи»). Доказано, что число
(читается «пи»). Доказано, что число 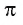 — иррациональное, то есть выражается бесконечной непериодической десятичной дробью. Приближенное значение числа л с точностью до восьми знаков после запятой такое:
— иррациональное, то есть выражается бесконечной непериодической десятичной дробью. Приближенное значение числа л с точностью до восьми знаков после запятой такое: 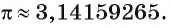 При решении задач в школьной практике пользуются приближенным значением числа
При решении задач в школьной практике пользуются приближенным значением числа 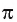 с точностью до сотых:
с точностью до сотых: 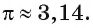
Длина дуги окружности
Для нахождения формулы длины окружности воспользуемся равенством 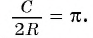 Отсюда следует, что длину окружности радиуса R можно найти по формуле
Отсюда следует, что длину окружности радиуса R можно найти по формуле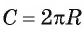 или по формуле
или по формуле 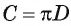 где D — диаметр окружности.
где D — диаметр окружности.
Теперь выведем формулу для вычисления длины I дуги окружности, градусная мера которой равна а. Пусть данная дуга является дугой окружности радиуса R. Так как длина всей окружности равна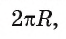 , то длина дуги в 1° равна
, то длина дуги в 1° равна
 . Так как градусная мера дуги равна а, то длина I этой дуги выражается:
. Так как градусная мера дуги равна а, то длина I этой дуги выражается: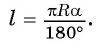
Пример №3
Точки F, Т и К — середины сторон равностороннего треугольника ABC. Найдите длину окружности, вписанной в треугольник FT К, если длина стороны треугольника ABC равна а.
Дано: 
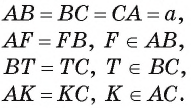
Найти: длину окружности, вписанной в треугольник 
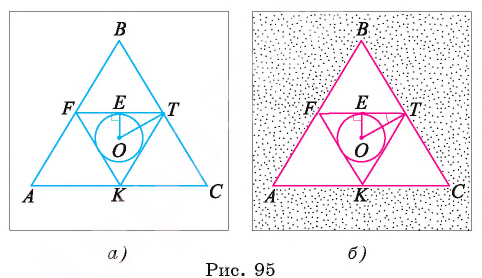
Решение:
Для нахождения длины окружности можем воспользоваться формулой 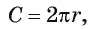 где г — радиус окружности, вписанной в треугольник FTK. Для нахождения радиуса г воспользуемся тем, что треугольник FTK также является равносторонним.
где г — радиус окружности, вписанной в треугольник FTK. Для нахождения радиуса г воспользуемся тем, что треугольник FTK также является равносторонним.
1) Пусть точка О — центр окружности, вписанной в треугольник FTK, а Е — точка касания окружности и стороны FT (рис. 95, а, б).
2) Треугольник FTK является равносторонним, так как 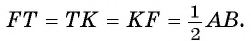 Треугольник ТЕО — прямоугольный,
Треугольник ТЕО — прямоугольный, 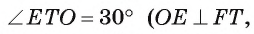 так как отрезок ОЕ — радиус, проведенный в точку касания, луч ОТ — биссектриса угла ЕТК).
так как отрезок ОЕ — радиус, проведенный в точку касания, луч ОТ — биссектриса угла ЕТК).
3) В прямоугольном треугольнике 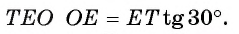 . Так как
. Так как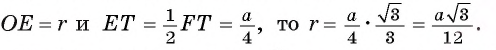
Заметим, что радиус г можно найти и другим способом, воспользовавшись тем, что треугольник FT К подобен треугольнику ABC с коэффициентом подобия 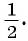
Таким образом, длина окружности 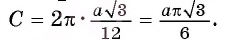
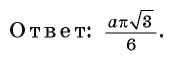
Пример №4
Основанием прямой четырехугольной призмы  является квадрат. Вычислите длину окружности, описанной около боковой грани призмы, если длина окружности, описанной около основания призмы, равна 871 см, а боковое ребро в два раза больше стороны основания призмы.
является квадрат. Вычислите длину окружности, описанной около боковой грани призмы, если длина окружности, описанной около основания призмы, равна 871 см, а боковое ребро в два раза больше стороны основания призмы.
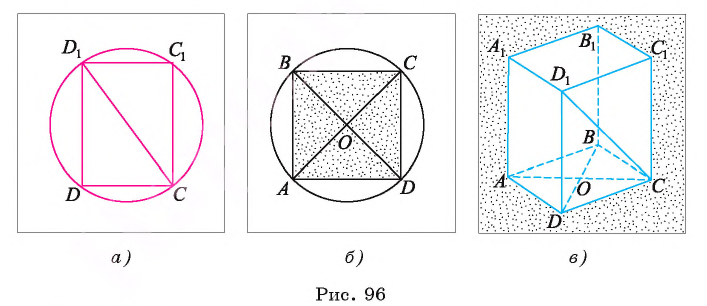
Решение:
Длину С окружности можно найти по формуле  где R — радиус окружности. Данная призма является прямой, и ее основаниями служат квадраты, следовательно, все боковые грани — равные между собой прямоугольники. Диагональ грани
где R — радиус окружности. Данная призма является прямой, и ее основаниями служат квадраты, следовательно, все боковые грани — равные между собой прямоугольники. Диагональ грани равна диаметру описанной около него окружности, т. е.
равна диаметру описанной около него окружности, т. е.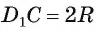 (рис. 96, а, б, в).
(рис. 96, а, б, в).
1) По условию длина окружности, описанной около квадрата ABCD, равна 8л см. Диаметр окружности равен диагонали АС, таким образом,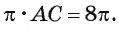 Отсюда АС = 8 см.
Отсюда АС = 8 см.
2) Так как четырехугольник ABCD — квадрат, то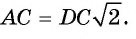 Следовательно,
Следовательно, 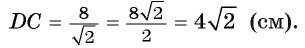
3) По условию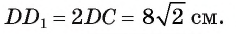 В прямоугольном треугольнике
В прямоугольном треугольнике 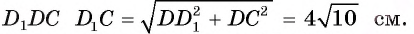 Диаметр окружности, описанной около грани
Диаметр окружности, описанной около грани 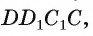 , равен
, равен 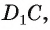 , т. е.
, т. е. 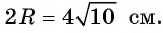 Теперь вычислим длину окружности, описанной около боковой грани
Теперь вычислим длину окружности, описанной около боковой грани 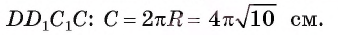 Ответ:
Ответ: 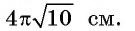
Радианная мера угла
Ранее была определена единица измерения углов — градус. Наряду с ней используется единица измерения углов, которая называется радианом.
Углом в один радиан называется центральный угол, которому соответствует длина дуги, равная длине радиуса окружности.
Радианная мера угла — это величина угла, выраженная в радианах.
Установим связь между радианной и градусной мерой угла. Углу, градусная мера которого равна 180°, соответствует полуокружность, длина I которой равна 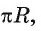 т. е.
т. е.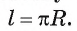 . Для нахождения радианной меры этого угла надо длину этой дуги разделить на радиус, т. е.
. Для нахождения радианной меры этого угла надо длину этой дуги разделить на радиус, т. е.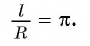 Следовательно, радианная мера развернутого угла равна л, т. е. 180° =
Следовательно, радианная мера развернутого угла равна л, т. е. 180° = 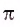 рад. Таким образом, радианная мера угла в 1°
рад. Таким образом, радианная мера угла в 1°
равна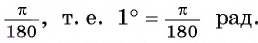 При записи используется сокращенное обозначение радиана — «рад». Из равенства
При записи используется сокращенное обозначение радиана — «рад». Из равенства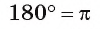 следует, что градусная мера
следует, что градусная мера
угла в 1 радиан равна 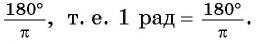 Приближенно 1 радиан равен 57°.Из определения радиана следует, что длина I дуги окружности радиуса R, соответствующей центральному углу в х радиан, равна Rx.
Приближенно 1 радиан равен 57°.Из определения радиана следует, что длина I дуги окружности радиуса R, соответствующей центральному углу в х радиан, равна Rx.
Рассмотрим примеры перехода от радианной меры к градусной и от градусной меры к радианной.
Пример №5
Вычислите градусную меру угла 3 рад.
Решение:
Так как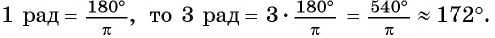
Пример №6
Вычислите радианную меру угла 30°.
Решение:
Так как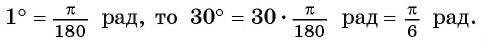
При записи радианной меры угла обозначение рад можно
опускать. Например, вместо  запишем
запишем 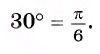
Площадь круга
Рассмотрим вопрос о вычислении площади круга. Пусть в окружность, ограничивающую круг, вписан правильный n-угольник. Если число n сторон правильного n-угольника, вписанного в окружность, неограниченно возрастает, то многоугольник все меньше и меньше отличается от круга (рис. 100, а, б). Из результатов, доказывемых в вузовском курсе математического анализа, следует, что существует число, к которому стремятся площади S,, правильных п-угольников, вписанных в окружность, при неограниченном возрастании числа их сторон. Это число называется площадью круга. Таким образом, за площадь круга принимается число, к которому стремятся площади вписанных в окружность, ограничивающую этот круг, правильных n-угольников при неограниченном увеличении числа их сторон.
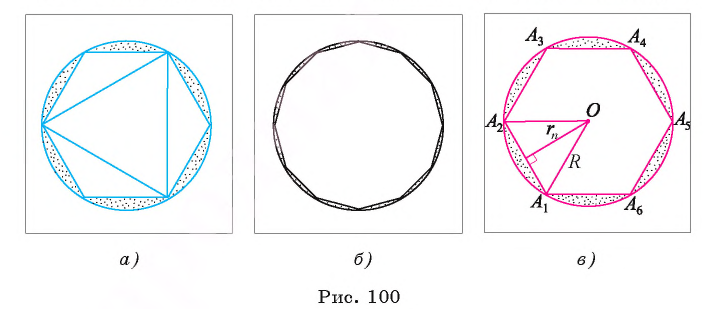
Теперь докажем следующую теорему.
Теорема (о площади круга). Площадь S круга радиуса R можно вычислить по формуле 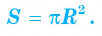
1) Пусть дан круг радиуса R и правильный n-угольник 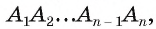 вписанный в окружность, которая ограничивает этот круг. На рисунке 100, в дано изображение для случая n = 6. Если
вписанный в окружность, которая ограничивает этот круг. На рисунке 100, в дано изображение для случая n = 6. Если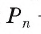 — периметр вписанного многоугольника, а г„ — радиус вписанной в него окружности, то S„ — площадь этого многоугольника, которая находится по формуле
— периметр вписанного многоугольника, а г„ — радиус вписанной в него окружности, то S„ — площадь этого многоугольника, которая находится по формуле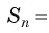
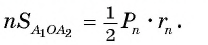
2) При неограниченном увеличении числа n сторон n-угольника радиус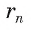 вписанной окружности стремится к R. Действительно, так как
вписанной окружности стремится к R. Действительно, так как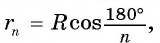 , то при неограниченном увеличении числа сторон n число
, то при неограниченном увеличении числа сторон n число 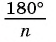 стремится к нулю, а значит,
стремится к нулю, а значит,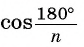 стремится к единице, т. е.
стремится к единице, т. е. 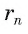 стремится к R. Кроме того, периметр
стремится к R. Кроме того, периметр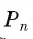 стремится к длине окружности, равной
стремится к длине окружности, равной 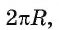 , а площадь
, а площадь 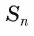 стремится к площади S круга. Таким образом, площадь круга
стремится к площади S круга. Таким образом, площадь круга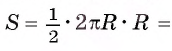
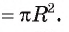
Теорема доказана.
Площадь сектора
Рассмотрим вопрос о вычислении площади части круга, которая называется сектором.
Определение. Сектором называется часть круга, ограниченная дугой окружности и двумя радиусами, соединяющими концы дуги с центром круга.
Дуга окружности, ограничивающая сектор, называется дугой сектора.
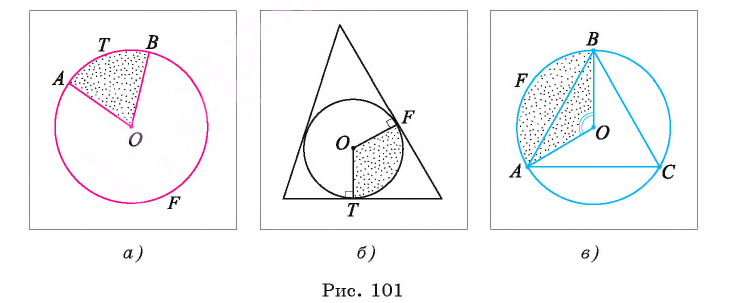
Например, на рисунке 101, а изображены два сектора, дугами которых служат дуги АТ В и AFB. На рисунке 101, б изображены круг, который касается всех сторон треугольника, и два сектора, ограниченные радиусами, проведенными в точки касания, и соответствующими дугами окружности.
Выведем формулу для вычисления площади S сектора радиуса R, градусная мера дуги которого равна а. Площадь круга радиуса R равна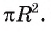 . Следовательно, площадь сектора, ограниченного дугой, градусная мера которой 1°, равна
. Следовательно, площадь сектора, ограниченного дугой, градусная мера которой 1°, равна
 Значит, площадь сектора, ограниченного дугой, градусная мера которой равна а градусов, можно найти по формуле
Значит, площадь сектора, ограниченного дугой, градусная мера которой равна а градусов, можно найти по формуле 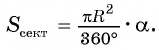
Например, если ABC — равносторонний треугольник, вписанный в круг радиуса R, а точка О — его центр, тогда площадь сектора, ограниченного радиусами ОА, ОБ и дугой AFB, равна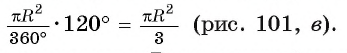
Площадь сегмента
Рассмотрим формулу для нахождения площади фигуры, которая называется сегментом.
Определение. Сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы дуги.
Дуга окружности, ограничивающая сегмент, называется дугой сегмента, а ограничивающая его хорда называется основанием сегмента.
На рисунке 102, а изображены два сегмента, ограниченные хордой АВ и дугами AFB и АТ В. Хорда АВ является основанием для каждого из этих сегментов.
На рисунке 102, б изображены сегменты, ограниченные стороной CD вписанного квадрата и соответствующими дугами окружности.
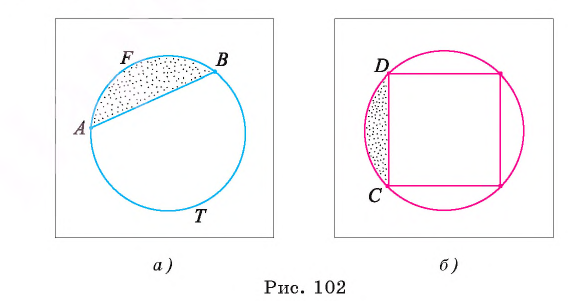
Выведем формулу для вычисления площади сегмента. Рассмотрим два случая: 1) градусная мера дуги сегмента меньше 180°; 2) градусная мера дуги сегмента больше 180°.
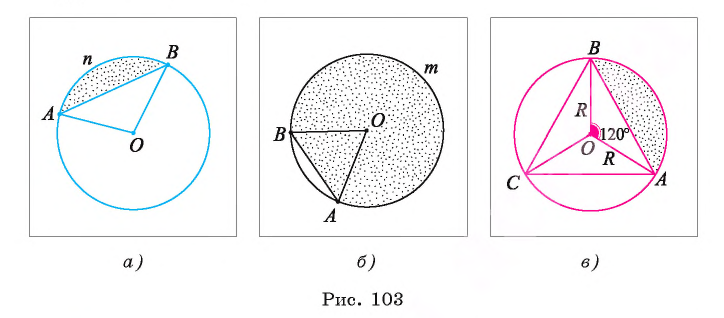
1) Пусть градусная мера дуги АnВ сегмента равна а 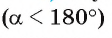 (рис. 103, а). Тогда площадь этого сегмента равна разности площади сектора, ограниченного этой дугой и радиусами ОА, ОВ, и площади треугольника АОВ, т. е.
(рис. 103, а). Тогда площадь этого сегмента равна разности площади сектора, ограниченного этой дугой и радиусами ОА, ОВ, и площади треугольника АОВ, т. е.
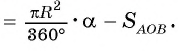
2) Пусть градусная мера дуги АmВ равна а (а > 180°) (рис. 103, б). Тогда площадь этого сегмента равна сумме площади сектора, ограниченного этой дугой и радиусами ОА,OB и площади треугольника, т. е. 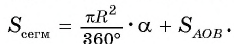
Заметим, что площадь этого сегмента можно найти так же, как разность между площадью круга и площадью сегмента с тем же основанием и дугой, градусная мера которой равна 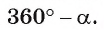
Пусть равносторонний треугольник ABC вписан в крут радиуса R, а точка О — его центр (рис. 103, в). Тогда площадь меньшего сегмента, основанием которого служит сторона АВ треугольника, равна 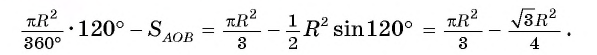
Пример №7
Диагональ BD равнобедренной трапеции ABCD перпендикулярна боковой стороне, а площадь круга, вписанного в треугольник ABD, равна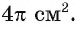 Вычислите длину окружности, описанной около трапеции, если площадь треугольника ABD равна
Вычислите длину окружности, описанной около трапеции, если площадь треугольника ABD равна 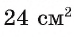 (рис. 104).
(рис. 104).
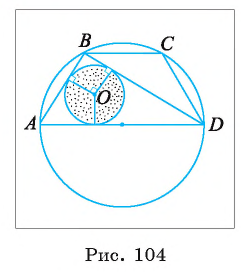
Решение:
Длину С окружности, описанной около трапеции ABCD, можно найти по формуле 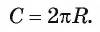 По условию задачи окружность, описанная около трапеции, описана около прямоугольного треугольника ABD. Следовательно, основание AD трапеции является диаметром окружности, т. е.
По условию задачи окружность, описанная около трапеции, описана около прямоугольного треугольника ABD. Следовательно, основание AD трапеции является диаметром окружности, т. е. 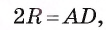 , а значит,
, а значит, 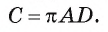
1) Пусть г — радиус круга, вписанного в треугольник ABD. Так как площадь этого круга равна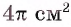 то из уравнения
то из уравнения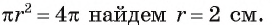
2) Площадь 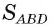 , прямоугольного треугольника ABD найдем по формуле
, прямоугольного треугольника ABD найдем по формуле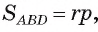 где г — радиус вписанного круга, р — полупериметр треугольника ABD. По условию задачи
где г — радиус вписанного круга, р — полупериметр треугольника ABD. По условию задачи 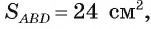 следовательно, из уравнения 24 = 2р получим р = 12 см.
следовательно, из уравнения 24 = 2р получим р = 12 см.
3) Для нахождения длины отрезка AD воспользуемся формулой r=p -AD. Отсюда AD =р – г = 12 – 2 = 10 (см).
4) Теперь длина окружности 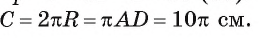
Ответ: 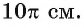
Пример №8
Основанием прямой треугольной призмы является равносторонний треугольник ABC. Вычислите длину окружности, описанной около боковой грани призмы, если площадь круга, вписанного в основание, равна
является равносторонний треугольник ABC. Вычислите длину окружности, описанной около боковой грани призмы, если площадь круга, вписанного в основание, равна 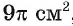 , а все ребра призмы равны между собой (рис. 105, а).
, а все ребра призмы равны между собой (рис. 105, а).
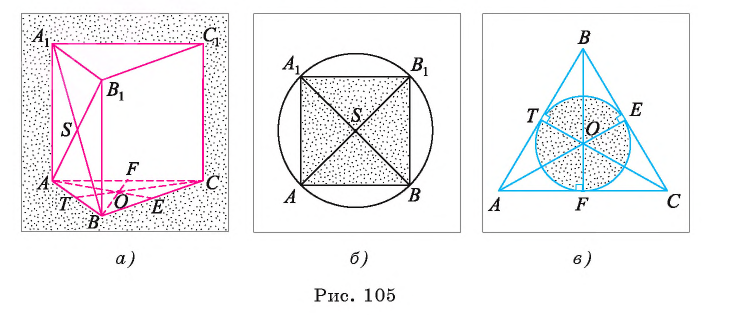
Решение:
По условию задачи каждая боковая грань призмы является квадратом. Длину окружности, описанной около квадрата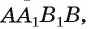 , можно вычислить по формуле
, можно вычислить по формуле 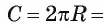
 Для нахождения длины стороны АВ можем воспользоваться тем, что по условию задачи известна площадь круга, вписанного в равносторонний треугольник ABC (рис. 105, б).
Для нахождения длины стороны АВ можем воспользоваться тем, что по условию задачи известна площадь круга, вписанного в равносторонний треугольник ABC (рис. 105, б).
1) Пусть точка О — центр круга, вписанного в равносторонний треугольник ABC, 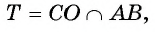 тогда АВ = 2АТ.
тогда АВ = 2АТ.
2) Так как площадь круга, вписанного в треугольник ABC, равна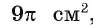 , то из уравнения
, то из уравнения 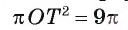 найдем ОТ = = 3 см.
найдем ОТ = = 3 см.
3) В прямоугольном треугольнике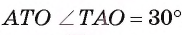 , следовательно,
, следовательно,
4) Теперь вычислим длину С окружности, описанной около грани 
Ответ: 
Правильные многоугольники с примерами
Определение. Правильным многоугольником называется выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунке 198 изображены правильные треугольник, четырехугольник, пятиугольник, шестиугольник, семиугольник. Правильный треугольник — это равносторонний треугольник, а правильный четырехугольник — это квадрат.
Одной из простейших задач является задача нахождения величины внутреннего угла правильного многоугольника. Так как все углы правильного 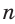 -угольника равны между собой, а сумма углов любого
-угольника равны между собой, а сумма углов любого 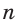 -угольника равна
-угольника равна 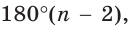 то угол
то угол 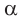 правильного
правильного 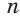 -угольника можно найти по формуле
-угольника можно найти по формуле
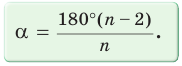
Например, для правильного шестиугольника 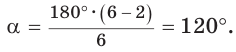
Теорема. Около любого правильного многоугольника можно описать окружность, в любой правильный многоугольник можно вписать окружность; центры этих окружностей совпадают.
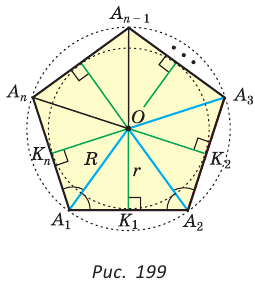
Доказательство:
В правильном многоугольнике 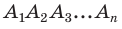 проведем биссектрисы внутренних углов
проведем биссектрисы внутренних углов 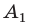 и
и 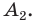 Пусть О — точка пересечения этих биссектрис (рис. 199). Так как
Пусть О — точка пересечения этих биссектрис (рис. 199). Так как 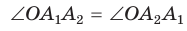 как половины равных углов, то
как половины равных углов, то  — равнобедренный с основанием
— равнобедренный с основанием  Проведя отрезок
Проведя отрезок  получим
получим  равный
равный 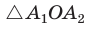 по двум сторонам и углу между ними (
по двум сторонам и углу между ними (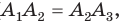 сторона
сторона 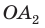 — общая,
— общая, 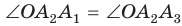 ).
).
Соединив точку О отрезками с остальными вершинами, получим множество равных равнобедренных треугольников. Отсюда 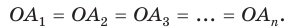
Поэтому окружность с центром О и радиусом 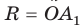 пройдет через все вершины многоугольника
пройдет через все вершины многоугольника 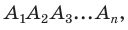 т. е. будет его описанной окружностью.
т. е. будет его описанной окружностью.
А поскольку высоты указанных равных равнобедренных треугольников, проведенные к их основаниям, равны, т. е. 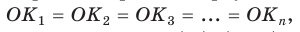 то точка О — также и центр вписанной окружности многоугольника
то точка О — также и центр вписанной окружности многоугольника 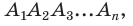 радиус которой
радиус которой 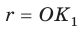 . Теорема доказана.
. Теорема доказана.
Точка О называется центром правильного  -угольника.
-угольника.
Формулы радиусов описанной и вписанной окружностей правильного многоугольника
Пусть 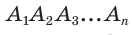 — правильный
— правильный 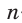 -угольник со стороной
-угольник со стороной 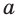 , где О — его центр,
, где О — его центр, 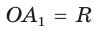 — радиус описанной окружности,
— радиус описанной окружности, 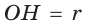 — радиус вписанной окружности (рис. 202).
— радиус вписанной окружности (рис. 202).
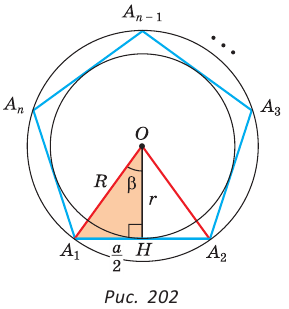
Так как  а высота ОН равнобедренного треугольника
а высота ОН равнобедренного треугольника  является биссектрисой и медианой, то угол
является биссектрисой и медианой, то угол 
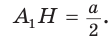 Из прямоугольного треугольника
Из прямоугольного треугольника 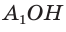 находим:
находим:
а) 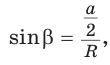 откуда
откуда 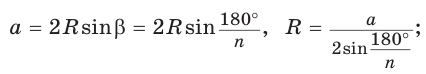
б) 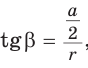 откуда
откуда 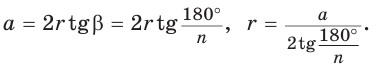
Замечание. Выведенные формулы запоминать не обязательно. Важно помнить способ их получения: решение прямоугольного треугольника 
Примеры:
1) Для правильного треугольника (рис. 203) получим:
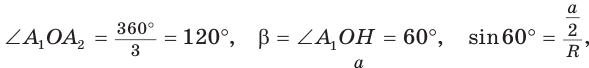 откуда
откуда 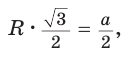
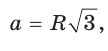 или
или 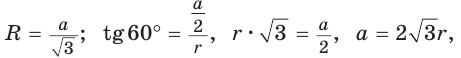 или
или 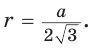
2) Для правильного четырехугольника (рис. 204) получим:
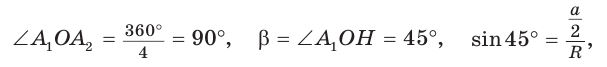 откуда
откуда 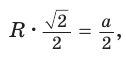
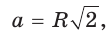 или
или 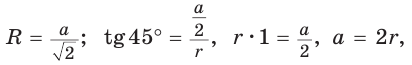 или
или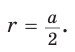
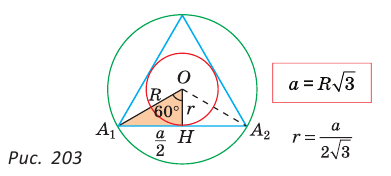
3) Для правильного шестиугольника (рис. 205) 
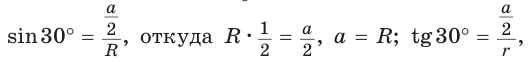
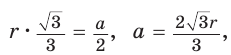 или
или 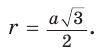
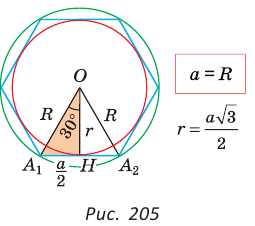
Полезно запомнить формулы, выражающие сторону 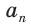 правильного
правильного  -угольника через радиус R описанной окружности при
-угольника через радиус R описанной окружности при  = 3, 4, 6:
= 3, 4, 6:
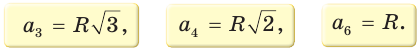
Для нахождения площади правильного 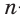 -угольника
-угольника 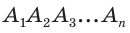 с центром О и радиусом R описанной окружности можно найти площадь треугольника
с центром О и радиусом R описанной окружности можно найти площадь треугольника  по формуле
по формуле 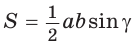 и умножить ее на число таких треугольников, т. е. на
и умножить ее на число таких треугольников, т. е. на 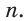
Пример:
Для нахождения радиуса 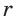 окружности, вписанной в правильный многоугольник, можно использовать формулу площади описанного многоугольника
окружности, вписанной в правильный многоугольник, можно использовать формулу площади описанного многоугольника 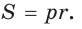
Правильный треугольник
Обобщим информацию о правильном (равностороннем) треугольнике.
Запишем формулы высоты 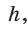 площади
площади 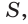 радиуса R описанной и радиуса
радиуса R описанной и радиуса  вписанной окружностей правильного треугольника АВС со стороной
вписанной окружностей правильного треугольника АВС со стороной  (рис. 209):
(рис. 209):
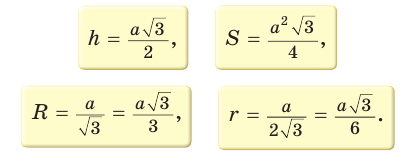
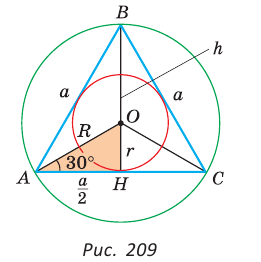
Из  где
где  , следует, что
, следует, что 
При заданной стороне  правильного треугольника его можно построить при помощи циркуля и линейки, используя алгоритм построения треугольника по трем сторонам.
правильного треугольника его можно построить при помощи циркуля и линейки, используя алгоритм построения треугольника по трем сторонам.
Так как 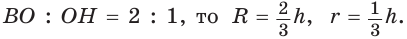 Для построения описанной и вписанной оружностей правильного треугольника достаточно по- строить его медианы (высоты), точка пересечения которых будет центром искомых окружностей.
Для построения описанной и вписанной оружностей правильного треугольника достаточно по- строить его медианы (высоты), точка пересечения которых будет центром искомых окружностей.
Правильный четырехугольник
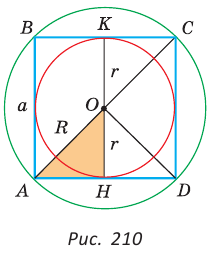
Пусть сторона квадрата ABCD равна  — радиус описанной,
— радиус описанной, 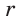 — радиус вписанной окружности (рис. 210). Диаметр его описанной окружности равен диагонали АС. В свою очередь,
— радиус вписанной окружности (рис. 210). Диаметр его описанной окружности равен диагонали АС. В свою очередь, 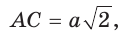 откуда
откуда 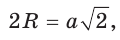 или
или 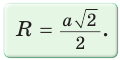 Из равнобедренного прямоугольного треугольника
Из равнобедренного прямоугольного треугольника 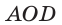 также следует, что
также следует, что 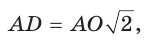
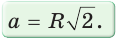
Диаметр КН окружности, вписанной в квадрат, равен длине стороны квадрата, т. е. КН = АВ = а, откуда 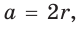
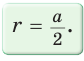 [ Из прямоугольного равнобедренного треугольника АОН также следует,
[ Из прямоугольного равнобедренного треугольника АОН также следует,
что 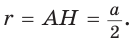
Для построения квадрата, вписанного в данную окружность с заданным центром, можно построить две взаимно перпендикулярные прямые, проходящие через центр окружности (рис. 211). Эти прямые пересекут окружность в вершинах квадрата. Обоснуйте это утверждение. Выполните указанное построение при помощи чертежного треугольника.
Правильный шестиугольник
Рассмотрим правильный 6-угольник ABCDEF со стороной  вписанный в окружность с центром О и радиусом R (рис. 212). Его внутренние углы равны по 120°. Треугольник AOF равнобедренный,
вписанный в окружность с центром О и радиусом R (рис. 212). Его внутренние углы равны по 120°. Треугольник AOF равнобедренный,
так как ОА = OF = R, 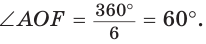 Поэтому
Поэтому  — равносторонний, откуда
— равносторонний, откуда 
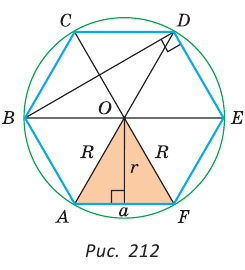
Так как радиус 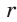 вписанной окружности является высотой равностороннего треугольника со стороной а, то
вписанной окружности является высотой равностороннего треугольника со стороной а, то 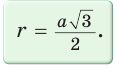
Поскольку  то большая (главная) диагональ BE правильного шестиугольника проходит через его центр О, а все три большие диагонали AD, BE и CF разбивают его на шесть равных равносторонних треугольников. Площадь правильного шестиугольника
то большая (главная) диагональ BE правильного шестиугольника проходит через его центр О, а все три большие диагонали AD, BE и CF разбивают его на шесть равных равносторонних треугольников. Площадь правильного шестиугольника
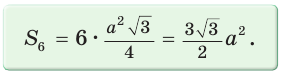
Меньшая (малая) диагональ BD правильного шестиугольника является диагональю ромба BCDO (ВС = CD = DO = ВО – а) с углами, равными 60° и 120°. Откуда 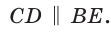 Треугольник BDE является прямоугольным (
Треугольник BDE является прямоугольным (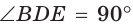 как опирающийся на диаметр),
как опирающийся на диаметр), 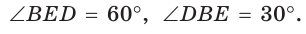
Кроме того, 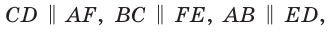 а расстояния между указанными парами параллельных прямых равны
а расстояния между указанными парами параллельных прямых равны 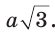 Докажите это самостоятельно.
Докажите это самостоятельно.
Построим при помощи циркуля и линейки правильный шестиугольник, вписанный в данную окружность с радиусом R (рис. 213, а). Воспользуемся тем, что а = R, где а — сторона правильного шестиугольника.
Одну вершину 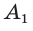 шестиугольника берем на окружности произвольно. Из нее как из центра радиусом, равным радиусу R, делаем засечку на окружности и получаем вершину
шестиугольника берем на окружности произвольно. Из нее как из центра радиусом, равным радиусу R, делаем засечку на окружности и получаем вершину  Затем аналогично последовательно строим остальные вершины:
Затем аналогично последовательно строим остальные вершины: 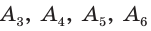 — и соединяем их отрезками. Из равенства равносторонних треугольников (
— и соединяем их отрезками. Из равенства равносторонних треугольников (
 ) следует равенство углов построенного шестиугольника
) следует равенство углов построенного шестиугольника  откуда заключаем, что он — правильный.
откуда заключаем, что он — правильный.
Для построения правильного треугольника, вписанного в данную окружность, достаточно соединить отрезками через одну вершины правильного вписанного шестиугольника (рис. 213, б). Для построения правильного 12-угольника следует разделить дуги 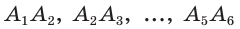 пополам (построив серединные перпендикуляры к сторонам правильного шестиугольника) и каждую из точек деления соединить отрезками с концами соответствующей стороны.
пополам (построив серединные перпендикуляры к сторонам правильного шестиугольника) и каждую из точек деления соединить отрезками с концами соответствующей стороны.
Применяя указанный способ деления дуг пополам, можно с помощью циркуля и линейки построить множество правильных многоугольников.
Так, из правильного 4-угольника можно построить правильный 8-угольник, 16-угольник, и вообще любой правильный 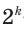 -угольник, где
-угольник, где 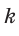 — целое число, большее двух.
— целое число, большее двух.
Пример №9
В окружности с центром О проведен диаметр BD, через середину радиуса OD проведена хорда АС, перпендикулярная диаметру BD (рис. 214). Доказать, что 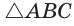 — правильный.
— правильный.
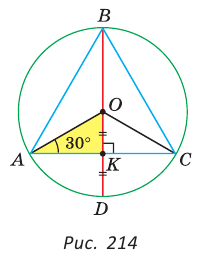
Доказательство:
Так как  то в прямоугольном треугольнике
то в прямоугольном треугольнике  . В равнобедренном треугольнике
. В равнобедренном треугольнике 
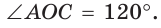 Вписанный угол АВС равен половине центрального угла АОС, т. е.
Вписанный угол АВС равен половине центрального угла АОС, т. е. 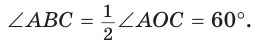 Диаметр, перпендикулярный хорде, делит ее пополам.
Диаметр, перпендикулярный хорде, делит ее пополам.
Поэтому АК = КС. Так как в треугольнике АВС высота ВК является и медианой, то он — равнобедренный, АВ = ВС. Отсюда 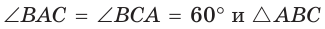 — равносторонний, т. е. правильный. Что и требовалось доказать.
— равносторонний, т. е. правильный. Что и требовалось доказать.
Замечание. Из задачи следует второй способ построения правильного треугольника, вписанного в окружность: строится диаметр BD, через середину радиуса OD проводится хорда АС, перпендикулярная диаметру. Треугольник АВС — правильный.
Пример №10
Дан правильный шестиугольник ABCDEF, диагональ АС равна 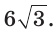 Найти площадь шестиугольника (рис. 215).
Найти площадь шестиугольника (рис. 215).
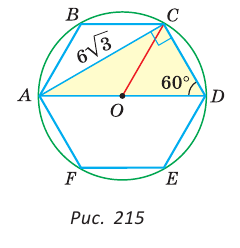
Решение:
Вписанный угол ACD опирается на диаметр АО, поэтому он прямой. Из прямоугольного треугольника 
Ответ: 
Нахождение длины окружности и площади круга
Длину окружности, сделанной из гибкой проволоки, можно измерить, если проволоку распрямить в отрезок. Еще древние заметили, что отношение длины любой окружности к ее диаметру есть величина постоянная: длина окружности примерно в 3 раза больше диаметра. Вы можете убедиться в этом при помощи нитки и линейки, используя в качестве окружности верхнюю кромку чашки (рис. 224).

Понятно, что периметр правильного многоугольника, вписанного в окружность, будет стремиться к длине окружности при неограниченном увеличении числа его сторон, а площадь этого многоугольника — к площади круга, ограниченного данной окружностью (рис. 225).
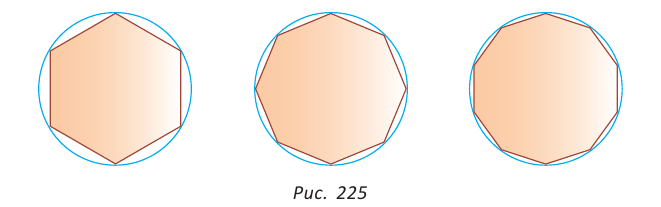
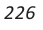
Используя этот факт, выведем уже известные вам формулы длины окружности 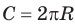 и площади круга
и площади круга 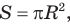 где R — радиус окружности и круга.
где R — радиус окружности и круга.
Вначале покажем, что отношение длины любой окружности С к ее диаметру D = 2R есть величина постоянная. Для этого рассмотрим две окружности и два правильных вписанных в них многоугольника с одинаковым числом сторон  где
где 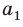 — сторона первого,
— сторона первого, 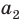 — сторона второго многоугольника,
— сторона второго многоугольника, 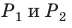 — их соответствующие периметры,
— их соответствующие периметры,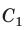 — длина первой, а
— длина первой, а 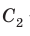 — длина второй описанной окружности (рис. 226).
— длина второй описанной окружности (рис. 226).
Найдем отношение указанных периметров:
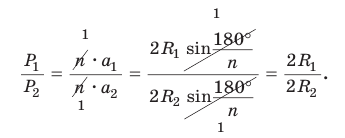
При неограниченном увеличении числа  периметр
периметр  устремится к
устремится к  периметр
периметр 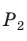 -к
-к 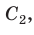 , а отношение
, а отношение 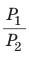 — к отношению
— к отношению 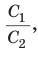 и тогда
и тогда 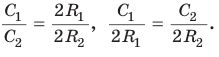
Отсюда следует, что отношение длины окружности к ее диаметру, т. е. . 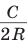 величина постоянная для любой окружности.
величина постоянная для любой окружности.
Это отношение обозначается буквой 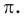 Так как
Так как 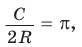 то длина окружности
то длина окружности 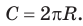 Таким образом, нами доказана следующая теорема.
Таким образом, нами доказана следующая теорема.
Теорема. Длина окружности радиуса R находится по формуле 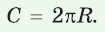
Интересно знать. Число 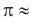 3,1415… — иррациональное и в десятичном виде представляет собой бесконечную непериодическую дробь. Оно было известно уже древним грекам. Еще Архимед нашел дробь
3,1415… — иррациональное и в десятичном виде представляет собой бесконечную непериодическую дробь. Оно было известно уже древним грекам. Еще Архимед нашел дробь 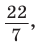 довольно точно приближающую число
довольно точно приближающую число 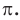 Мы же для приближенных вычислений будем пользоваться в основном значением
Мы же для приближенных вычислений будем пользоваться в основном значением 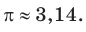
А теперь выведем формулу площади круга.
Теорема. Площадь круга радиуса R находится по формуле
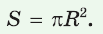
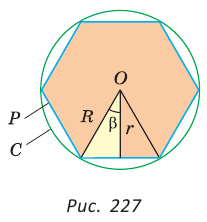
Доказательство:
Рассмотрим некоторую окружность радиуса R и вписанный в нее правильный 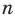 -угольник (рис. 227), площадь которого
-угольник (рис. 227), площадь которого 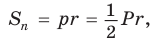 где Р — его периметр,
где Р — его периметр, 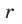 — радиус вписанной окружности. При неограниченном увеличении числа
— радиус вписанной окружности. При неограниченном увеличении числа 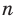 площадь
площадь 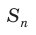 правильного
правильного  -угольника устремится к площади
-угольника устремится к площади 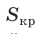 круга радиуса R, периметр Р — к длине С описанной окружности, а радиус
круга радиуса R, периметр Р — к длине С описанной окружности, а радиус 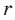 — к радиусу R (поскольку угол р устремится к нулю).
— к радиусу R (поскольку угол р устремится к нулю).
Тогда 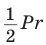 устремится к
устремится к 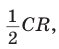 то есть к
то есть к 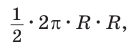 что равно
что равно 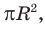 откуда
откуда 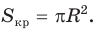
Теорема доказана.
Длина дуги окружности и площадь сектора круга
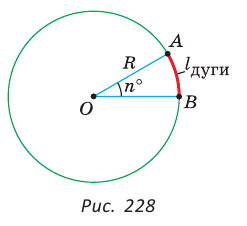
Поскольку длина окружности 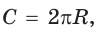 а ее градусная мера равна 360°, то длина дуги, содержащей 1°, равна
а ее градусная мера равна 360°, то длина дуги, содержащей 1°, равна 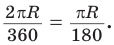 Тогда длина
Тогда длина  дуги, содержащей
дуги, содержащей 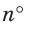 (рис. 228), равна
(рис. 228), равна 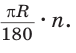
Напомним, что сектором называется часть круга, ограниченная двумя радиусами и дугой, соединяющей концы радиусов (рис. 229). Радиус круга называется радиусом сектора, указанная дуга — дугой сектора, центральный угол между радиусами, ограничивающими сектор, — углом сектора.
Так как площадь круга 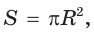 то площадь сектора с углом в 1° равна
то площадь сектора с углом в 1° равна 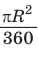 , а с углом в
, а с углом в  градусов —
градусов — 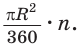
Заметим, что 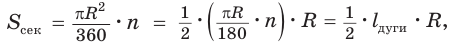 т. е. площадь сектора равна половине произведения длины дуги сектора на его радиус.
т. е. площадь сектора равна половине произведения длины дуги сектора на его радиус.
Пример №11
Пусть дана дуга окружности с радиусом 9 см, содержащая 30° (рис. 230, а). Найдем длину дуги:
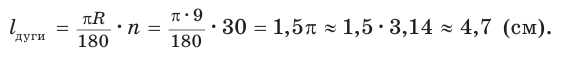
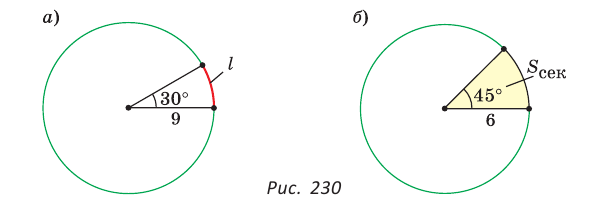
Пример №12
Пусть угол сектора содержит 45°, а радиус равен 6 см (рис. 230, б). Найдем площадь сектора:
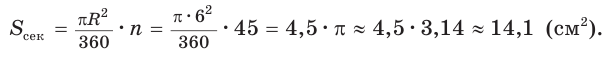
Замечание. При вычислении длины дуги (площади сектора) допустимы обе следующие записи:
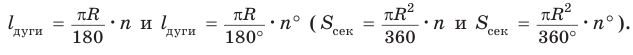
Длина дуги и площадь сектора прямо пропорциональны градусной мере дуги и угла сектора. Поэтому длина дуги так относится к длине окружности, как градусная мера дуги относится к градусной мере окружности.
Площадь сектора так относится к площади круга, как градусная мера угла сектора относится к градусной мере полного угла, т. е. справедливы пропорции:
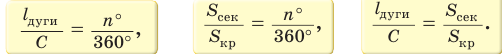
Замечание. В третьей пропорции  — это длина дуги сектора.
— это длина дуги сектора.
Данные пропорции также позволяют находить длину дуги и площадь сектора. Так, если длина окружности равна 10 см, а градусная мера ее дуги 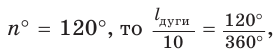 откуда длина данной дуги
откуда длина данной дуги 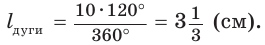
А если площадь круга равна 12 см2 и угол сектора равен 80°, 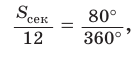 откуда площадь данного сектора
откуда площадь данного сектора 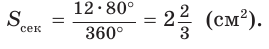
Пример №13
Дан сектор АОВ (рис. 231), радиус которого равен 6, а площадь —  . Найти длину дуги этого сектора. Ответ округлить до 0,1.
. Найти длину дуги этого сектора. Ответ округлить до 0,1.
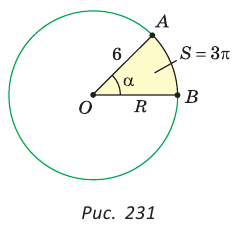
Решение:
Способ 1. Пусть  откуда
откуда  Так как по условию
Так как по условию  то
то 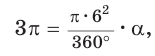 откуда
откуда 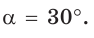 Найдем длину дуги
Найдем длину дуги 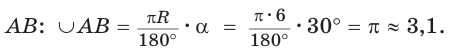
Способ 2. Воспользуемся пропорцией 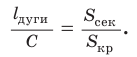
Тогда 
Способ 3. Так как 
Ответ: 3,1.
Пример №14
Найти площадь сегмента круга, радиус которого равен 12, если градусная мера дуги этого сегмента равна 120°.
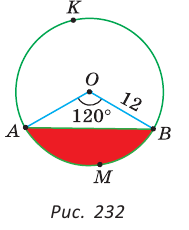
Решение:
Напомним, что сегментом называется часть круга, ограниченная хордой и дугой окружности, которая соединяет концы этой хорды.
Пусть О — центр данной окружности, 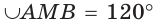 (рис. 232). Тогда
(рис. 232). Тогда 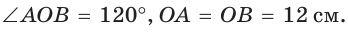 Площадь сегмента АМВ равна разности площади сектора АОВМ и площади равнобедренного треугольника АОВ.
Площадь сегмента АМВ равна разности площади сектора АОВМ и площади равнобедренного треугольника АОВ.
Так как площадь сектора 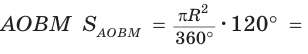
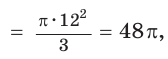 а площадь треугольника
а площадь треугольника 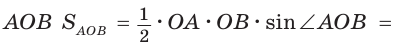
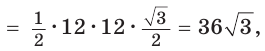 то площадь сегмента
то площадь сегмента 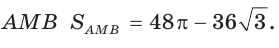
Ответ: 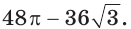
Замечание. Площадь сегмента АКВ (см. рис. 232) можно найти как сумму площадей сектора ОАКВ и треугольника АОВ, либо как разность площади круга и площади сегмента АМВ.
Интересно знать. В 1987 г. был учрежден неофициальный праздник — день числа 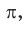 который отмечают любители математики 14 марта (3-й месяц, 14-е число).
который отмечают любители математики 14 марта (3-й месяц, 14-е число).
Долгое время математики старались найти как можно большее число знаков числа 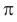 после запятой.
после запятой.
Легко запомнить двенадцать первых знаков числа 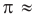 3,14159265358… при помощи следующей считалки: «Это я знаю и помню прекрасно, но многие цифры мне лишни, напрасны», — в которой количество букв в каждом слове означает очередную цифру числа
3,14159265358… при помощи следующей считалки: «Это я знаю и помню прекрасно, но многие цифры мне лишни, напрасны», — в которой количество букв в каждом слове означает очередную цифру числа 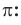 «это» — 3, «я» — 1, «знаю» — 4 и т. д.
«это» — 3, «я» — 1, «знаю» — 4 и т. д.
Луночки Гиппократа
Луночками Гиппократа называют серповидные фигуры, ограниченные дугами двух окружностей.
Пример №15
На отрезках АВ, AM и МВ построены полукруги с центрами в точках  (рис. 249). Найти площадь закрашенной части большого полукруга.
(рис. 249). Найти площадь закрашенной части большого полукруга.
Решение:
Площадь закрашенной фигуры равна разности площадей полукруга с диаметром АВ = 2R и двух полукругов с диаметрами  и
и  т. е.
т. е.
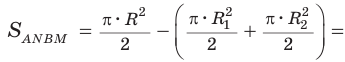
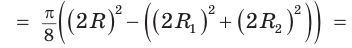
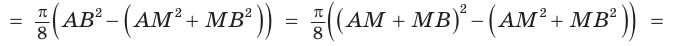
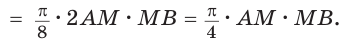
Так как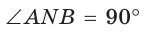 как вписанный угол, опирающийся на диаметр АВ, то NM — высота прямоугольного треугольника ANB, проведенная к гипотенузе. А высота прямоугольного треугольника, проведенная к гипотенузе, это среднее пропорциональное между проекциями катетов на гипотенузу, т. е.
как вписанный угол, опирающийся на диаметр АВ, то NM — высота прямоугольного треугольника ANB, проведенная к гипотенузе. А высота прямоугольного треугольника, проведенная к гипотенузе, это среднее пропорциональное между проекциями катетов на гипотенузу, т. е. 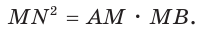 Следовательно,
Следовательно, 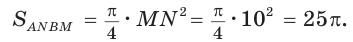
Ответ: 25л.
Золотое сечение
«Золотое сечение», или «божественная пропорция», — так называют математики деление отрезка некоторой точкой на части так, что больший из полученных отрезков является средним пропорциональным (средним геометрическим) между меньшим отрезком и целым. Другими словами, больший отрезок должен так относиться к меньшему, как целый отрезок относится к большему. Если на отрезке АВ отмечена точка М и 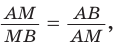 то отрезок AM — среднее пропорциональное отрезков АВ и МВ. Поэтому точка М делит отрезок АВ в отношении золотого сечения.
то отрезок AM — среднее пропорциональное отрезков АВ и МВ. Поэтому точка М делит отрезок АВ в отношении золотого сечения.
Пусть 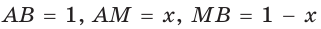 (рис. 251).
(рис. 251).
Тогда 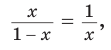 откуда
откуда 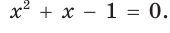 Учитывая, что
Учитывая, что  получим
получим 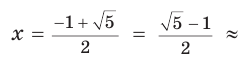
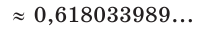
Таким образом, больший отрезок AM составляет приблизительно 62 %, а меньший отрезок МВ — приблизительно 38 % всего отрезка АВ.
Число 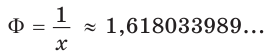 — считается отношением золотого сечения. Оно примерно равно отношению 8 : 5 (рис. 252).
— считается отношением золотого сечения. Оно примерно равно отношению 8 : 5 (рис. 252).
Золотое сечение обладает определенной гармонией, которую человек находит прекрасной. Многие художественные, музыкальные, поэтические произведения, шедевры архитектуры содержат в своей структуре золотое сечение. Опытным путем установлено, что оптимальным человеку кажется прямоугольник, длина и ширина которого находятся в отношении золотого сечения. Физиологи объясняют это тем, что поле зрения человека, т. е. та часть окружающего мира, которую видит человек, представляет собой прямоугольник со сторонами, находящимися в отношении золотого сечения.

Известно, например, что в знаменитой скульптуре Венеры Милосской (рис. 253) — эталоне женской красоты — талия делит фигуру в отношении золотого сечения.
Примечателен один исторический факт. Когда информация о Венере Милосской и золотом сечении была опубликована в одном из популярных журналов начала XX в., то в магазинах поблизости женских гимназий вдруг исчезли портняжные метры. Их раскупили девушки гимназистки, чтобы проверить, насколько их фигура близка к идеалу и какой высоты каблук следует носить, чтобы к нему приблизиться.
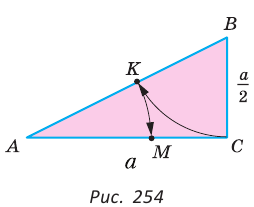
Покажем способ деления отрезка в отношении золотого сечения при помощи циркуля и линейки. Пусть дан отрезок, равный 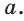 Построим прямоугольный треугольник АВС с катетами
Построим прямоугольный треугольник АВС с катетами 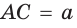 и
и 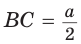 (рис. 254). На гипотенузе АВ отложим отрезок ВК, равный отрезку ВС. Затем на катете АС отложим отрезок AM, равный отрезку АК.
(рис. 254). На гипотенузе АВ отложим отрезок ВК, равный отрезку ВС. Затем на катете АС отложим отрезок AM, равный отрезку АК.
Точка М делит отрезок АС в отношении золотого сечения, т. е. 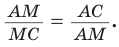 Убедитесь в этом самостоятельно.
Убедитесь в этом самостоятельно.
Построение правильного пятиугольника
С давних времен построению правильных многоугольников при помощи циркуля и линейки математики уделяли большое внимание. Древние греки умели строить правильные треугольники, четырехугольники, пятиугольники, а также правильные многоугольники, получаемые удвоением числа их сторон: 6-угольники, 8-угольники, 10-угольники и т. д. Далее дело зашло в тупик: они не могли найти способ построения правильных 7-угольников, 9-угольников, 11-угольников. И только 2000 лет спустя великий немецкий математик XVII в. Карл Гаусс решил эту математическую проблему. Будучи 19-летним юношей, он доказал, что можно построить правильный 17-угольник, а вот 7-угольник, 9-угольник, 11-угольник, 13-угольник циркулем и линейкой построить нельзя. Задача о построении правильного 17-угольника была его первым научным открытием. Несмотря на выдающиеся достижения Гаусса в области математики, этой пер вой своей решенной проблеме он придавал такое значение, что в конце жизни завещал изобразить на могильном камне правильный 17-угольник.
Рассмотрим правильный пятиугольник. Если в нем провести все диагонали (рис. 255), то получится звезда (звездчатый пятиугольник). Звезда была символом школы Пифагора. Замечательно то, что точки пересечения диагоналей пятиугольника делят их в отношении золотого сечения: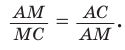 Докажем это.
Докажем это.
Так как  — равные равнобедренные треугольники (рис. 256), то
— равные равнобедренные треугольники (рис. 256), то  Поскольку
Поскольку 
 (докажите самостоятельно), то AMDE — параллелограмм, поэтому
(докажите самостоятельно), то AMDE — параллелограмм, поэтому 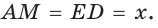
Но ВС = ED = х как стороны пятиугольника. Из подобия треугольников АВС и ВМС (по двум углам) следует 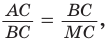 или
или 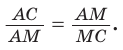 Следовательно, точка М делит отрезок АС в отношении золотого сечения.
Следовательно, точка М делит отрезок АС в отношении золотого сечения.
Рассмотрим задачу о построении правильного пятиугольника при помощи циркуля и линейки. Для построения правильного пятиугольника можно взять произвольный отрезок  равный диагонали правильного пятиугольника, и разделить его в отношении золотого сечения. Получив отрезок
равный диагонали правильного пятиугольника, и разделить его в отношении золотого сечения. Получив отрезок 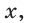 который равен стороне правильного пятиугольника, можно легко построить правильный пятиугольник. Продолжите построение сами.
который равен стороне правильного пятиугольника, можно легко построить правильный пятиугольник. Продолжите построение сами.
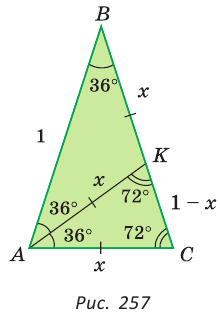
Задача о построении правильного пятиугольника равносильна построению углов, равных 36°, 72°, 108°, а также построению равнобедренного треугольника, биссектриса угла при основании которого разбивает данный треугольник на два равнобедренных. Пусть в треугольнике АВС (рис. 257)  — биссектриса и АВ = ВС = 1. Обозначим АС = АК = КВ = х, КС = 1 – х. Из свойства биссектрисы вытекает
— биссектриса и АВ = ВС = 1. Обозначим АС = АК = КВ = х, КС = 1 – х. Из свойства биссектрисы вытекает 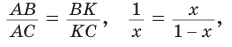 откуда
откуда 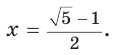 Таким образом, точка К делит отрезок ВС в отношении золотого сечения. Из треугольника АВС по теореме косинусов
Таким образом, точка К делит отрезок ВС в отношении золотого сечения. Из треугольника АВС по теореме косинусов
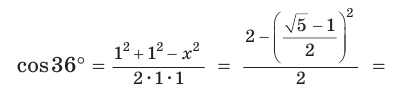
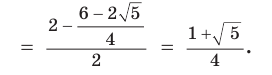
Отметим, что сторона АС треугольника АВС является стороной правильного десятиугольника, вписанного в окружность с радиусом, равным АВ.
Справочный материал по правильным многоугольникам
В этом параграфе вы узнаете, какие многоугольники называют правильными. Изучите свойства правильных многоугольников. Узнаете, как с помощью циркуля и линейки строить некоторые из них.
Научитесь находить радиусы вписанной и описанной окружностей правильного многоугольника, длину дуги окружности, площади сектора и сегмента круга.
Правильные многоугольники и их свойства
Определение. Многоугольник называют правильным, если у него все стороны равны и все углы равны.
С некоторыми правильными многоугольниками вы уже знакомы: равносторонний треугольник — это правильный треугольник, квадрат — это правильный четырехугольник. На рисунке 6.1 изображены правильные пятиугольник и восьмиугольник.
Ознакомимся с некоторыми свойствами, которыми обладают все правильные  -угольники.
-угольники.
Теорема 6.1. Правильный многоугольник является выпуклым многоугольником.
С доказательством этой теоремы вы можете ознакомиться на с. 61-62.
Каждый угол правильного 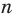 -угольника равен
-угольника равен  Действительно, поскольку сумма углов выпуклого
Действительно, поскольку сумма углов выпуклого  -угольника равна
-угольника равна 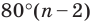 и все углы равны, то каждый из них равен
и все углы равны, то каждый из них равен 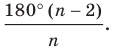
В правильном треугольнике существует точка, равноудаленная от всех его вершин и от всех его сторон. Это точка пересечения биссектрис правильного треугольника. Точка пересечения диагоналей квадрата также обладает аналогичным свойством. То, что в любом правильном многоугольнике существует точка, равноудаленная от всех его вершин и от всех его сторон, подтверждает следующая теорема.
Теорема 6.2. Любой правильный многоугольник является как вписанным в окружность, так и описанным около окружности, причем центры описанной и вписанной окружностей совпадают.
Доказательство: На рисунке 6.2 изображен правильный 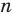 -угольник
-угольник  Докажем, что в него можно вписать и около него можно описать окружности.
Докажем, что в него можно вписать и около него можно описать окружности.
Проведем биссектрисы углов  Пусть
Пусть  — точка их пересечения. Соединим точки
— точка их пересечения. Соединим точки  Поскольку в треугольниках
Поскольку в треугольниках  и
и 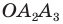 углы 2 и 3 равны,
углы 2 и 3 равны, 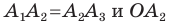 — общая сторона, то эти треугольники равны по первому признаку равенства треугольников. Кроме того, углы 1 и 2 равны как половины равных углов. Отсюда треугольник
— общая сторона, то эти треугольники равны по первому признаку равенства треугольников. Кроме того, углы 1 и 2 равны как половины равных углов. Отсюда треугольник 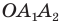 — равнобедренный, следовательно, равнобедренным является треугольник
— равнобедренный, следовательно, равнобедренным является треугольник 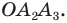 Поэтому
Поэтому 
Соединяя точку  с вершинами
с вершинами  аналогично можно показать, что
аналогично можно показать, что 
Таким образом, для многоугольника  существует точка, равноудаленная от всех его вершин. Это точка
существует точка, равноудаленная от всех его вершин. Это точка  — центр описанной окружности.
— центр описанной окружности.
Поскольку равнобедренные треугольники 
 равны, то равны и их высоты, проведенные из вершины
равны, то равны и их высоты, проведенные из вершины  Отсюда делаем вывод: точка
Отсюда делаем вывод: точка  равноудалена от всех сторон многоугольника. Следовательно, точка
равноудалена от всех сторон многоугольника. Следовательно, точка  — центр вписанной окружности.
— центр вписанной окружности. 
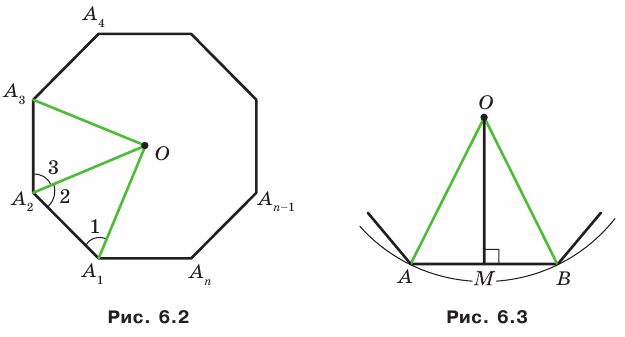
Точку, которая является центром описанной и вписанной окружностей правильного многоугольника, называют центром правильного многоугольника.
На рисунке 6.3 изображен фрагмент правильного  -угольника с центром
-угольника с центром  и стороной
и стороной 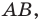 длину которой обозначим
длину которой обозначим 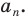 Угол
Угол 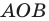 называют центральным углом правильного многоугольника. Понятно, что
называют центральным углом правильного многоугольника. Понятно, что 
В равнобедренном треугольнике  проведем высоту
проведем высоту  Тогда
Тогда 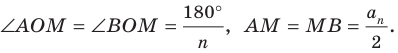 Из треугольника
Из треугольника  получаем, что
получаем, что
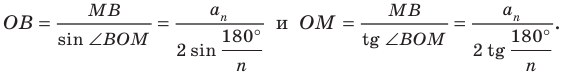
Отрезки  — радиусы соответственно описанной и вписанной окружностей правильного
— радиусы соответственно описанной и вписанной окружностей правильного 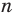 -угольника. Если длины этих радиусов обозначить
-угольника. Если длины этих радиусов обозначить  соответственно, то полученные результаты можно записать в виде формул:
соответственно, то полученные результаты можно записать в виде формул:
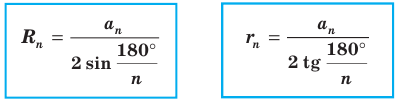
Подставив в эти формулы вместо  числа 3, 4, 6, получим формулы для нахождения радиусов описанной и вписанной окружностей для правильных треугольника, четырехугольника и шестиугольника со стороной
числа 3, 4, 6, получим формулы для нахождения радиусов описанной и вписанной окружностей для правильных треугольника, четырехугольника и шестиугольника со стороной 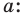

Из полученных результатов следует, что сторона правильного шестиугольника равна радиусу его описанной окружности. Отсюда получаем алгоритм построения правильного шестиугольника: от произвольной точки  окружности надо последовательно откладывать хорды, равные радиусу (рис. 6.4). Таким образом получаем вершины правильного шестиугольника.
окружности надо последовательно откладывать хорды, равные радиусу (рис. 6.4). Таким образом получаем вершины правильного шестиугольника.
Соединив через одну вершины правильного шестиугольника, получим правильный треугольник (рис. 6.5).
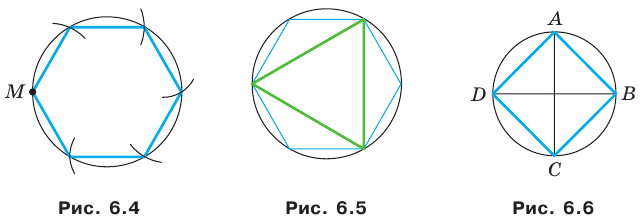
Для построения правильного четырехугольника достаточно в окружности провести два перпендикулярных диаметра  (рис. 6.6). Тогда четырехугольник
(рис. 6.6). Тогда четырехугольник 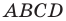 — квадрат (докажите это самостоятельно).
— квадрат (докажите это самостоятельно).
Если уже построен правильный 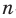 -угольник, то легко построить правильный
-угольник, то легко построить правильный 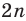 -угольник. Для этого надо найти середины всех сторон
-угольник. Для этого надо найти середины всех сторон 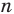 -угольника и провести радиусы описанной окружности через полученные точки. Тогда концы радиусов и вершины данного
-угольника и провести радиусы описанной окружности через полученные точки. Тогда концы радиусов и вершины данного  -угольника будут вершинами правильного
-угольника будут вершинами правильного  -угольника. На рисунках 6.7 и 6.8 показано построение правильных 8-угольника и 12-угольника.
-угольника. На рисунках 6.7 и 6.8 показано построение правильных 8-угольника и 12-угольника.
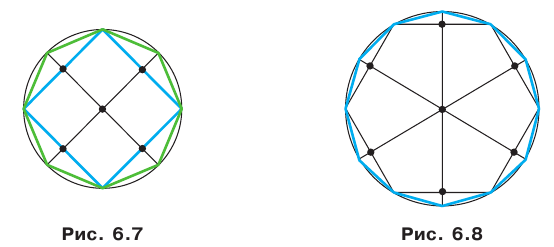
Пример №16
Существует ли правильный многоугольник, угол которого равен: 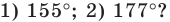 В случае утвердительного ответа укажите вид многоугольника.
В случае утвердительного ответа укажите вид многоугольника.
Решение:
1) Пусть 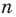 — количество сторон искомого правильного многоугольника. С одной стороны, сумма его углов равна
— количество сторон искомого правильного многоугольника. С одной стороны, сумма его углов равна 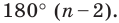
С другой стороны, эта сумма равна 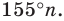 Следовательно,
Следовательно, 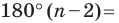
 Поскольку
Поскольку 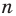 должно быть натуральным числом, то такого правильного многоугольника не существует.
должно быть натуральным числом, то такого правильного многоугольника не существует.
2) Имеем: 
Ответ: 1) не существует; 2) существует, это — стодвадцатиугольник.
Пример №17
В окружность вписан правильный треугольник со стороной 18 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.
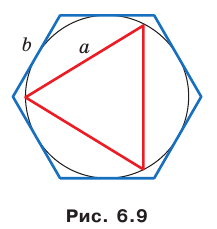
Решение:
Радиус окружности, описанной около правильного треугольника, вычисляют по формуле 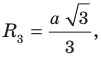 где
где 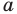 — длина стороны треугольника (рис. 6.9). Следовательно,
— длина стороны треугольника (рис. 6.9). Следовательно,
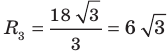 (см)
(см)
По условию радиус окружности, вписанной в правильный шестиугольник, равен радиусу окружности, описанной около правильного треугольника, то есть  см. Поскольку
см. Поскольку 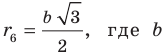 — длина стороны правильного шестиугольника, то
— длина стороны правильного шестиугольника, то
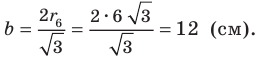
Ответ: 12 см. 
О построении правильных n-угольников
Докажем, что любой правильный  -угольник является выпуклым многоугольником. Для этого достаточно показать, что в любом многоугольнике есть хотя бы один угол, меньший
-угольник является выпуклым многоугольником. Для этого достаточно показать, что в любом многоугольнике есть хотя бы один угол, меньший  Тогда из того, что в правильном
Тогда из того, что в правильном 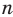 -угольнике все углы равны, будет следовать, что каждый из них меньше
-угольнике все углы равны, будет следовать, что каждый из них меньше  то есть многоугольник будет выпуклым.
то есть многоугольник будет выпуклым.
Рассмотрим произвольный многоугольник и прямую  не имеющую с ним общих точек (рис. 6.11). Из каждой вершины многоугольника опустим перпендикуляр на прямую
не имеющую с ним общих точек (рис. 6.11). Из каждой вершины многоугольника опустим перпендикуляр на прямую 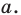
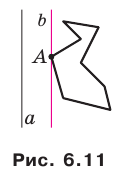
Сравнив длины этих перпендикуляров, мы сможем выбрать вершину многоугольника, наименее удаленную от прямой  (если таких вершин несколько, то выберем любую из них). Пусть этим свойством обладает вершина
(если таких вершин несколько, то выберем любую из них). Пусть этим свойством обладает вершина  (рис. 6.11). Через точку
(рис. 6.11). Через точку  проведем прямую
проведем прямую  параллельную прямой
параллельную прямой  Тогда угол
Тогда угол  многоугольника лежит в одной полуплоскости относительно прямой
многоугольника лежит в одной полуплоскости относительно прямой  Следовательно,
Следовательно, 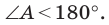
Вы умеете с помощью циркуля и линейки строить правильный 4-угольник, а следовательно, и 8-угольник, 16-угольник, 32-угольник, то есть любой 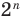 -угольник (
-угольник (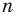 — натуральное число,
— натуральное число, 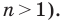 Умение строить правильный треугольник позволяет построить следующую цепочку из правильных многоугольников: 6-угольник, 12-угольник, 24-угольник и т. д., то есть любой
Умение строить правильный треугольник позволяет построить следующую цепочку из правильных многоугольников: 6-угольник, 12-угольник, 24-угольник и т. д., то есть любой 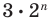 -угольник
-угольник  — натуральное число).
— натуральное число).
Задачу построения правильных многоугольников с помощью циркуля и линейки изучали еще древнегреческие геометры.
В частности, помимо указанных выше многоугольников, они умели строить правильные 5-угольник и 15-угольник — задачи довольно непростые.
Древние ученые, умевшие строить любой из правильных  -угольников, где
-угольников, где 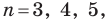
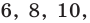 пытались решить эту задачу и для
пытались решить эту задачу и для 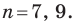 Им это не удалось. Вообще, более двух тысяч лет математики не могли продвинуться в решении этой проблемы. Лишь в 1796 г. великий немецкий математик Карл Фридрих Гаусс смог с помощью циркуля и линейки построить правильный 17-угольник. В 1801 г.
Им это не удалось. Вообще, более двух тысяч лет математики не могли продвинуться в решении этой проблемы. Лишь в 1796 г. великий немецкий математик Карл Фридрих Гаусс смог с помощью циркуля и линейки построить правильный 17-угольник. В 1801 г.
Гаусс доказал, что циркулем и линейкой можно построить правильный 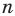 -угольник тогда и только тогда, когда
-угольник тогда и только тогда, когда 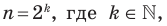
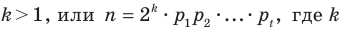 — целое неотрицательное число,
— целое неотрицательное число,  — разные простые числа вида
— разные простые числа вида  где
где  — целое неотрицательное число, которые называют простыми числами Ферма
— целое неотрицательное число, которые называют простыми числами Ферма Сейчас известны лишь пять простых чисел Ферма: 3, 5, 17, 257, 65 537.
Сейчас известны лишь пять простых чисел Ферма: 3, 5, 17, 257, 65 537.
Гаусс придавал своему открытию столь большое значение, что завещал изобразить 17-угольник на своем надгробии. На могильной плите Гаусса этого рисунка нет, однако памятник Гауссу в Браун-швейге стоит на семнадцатиугольном постаменте.
Длина окружности. Площадь круга
На рисунке 7.1 изображены правильные 4-угольник, 8-угольник и 16-угольник, вписанные в окружность.
Мы видим, что при увеличении количества сторон правильного 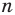 -угольника его периметр
-угольника его периметр 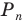 все меньше и меньше отличается от длины
все меньше и меньше отличается от длины  описанной окружности.
описанной окружности.
Так, для нашего примера можно записать:
При неограниченном увеличении количества сторон правильного многоугольника его периметр будет как угодно мало отличаться от длины окружности. Это означает, что разность  можно сделать меньшей, чем, например,
можно сделать меньшей, чем, например,  и вообще меньшей, чем любое положительное число.
и вообще меньшей, чем любое положительное число.
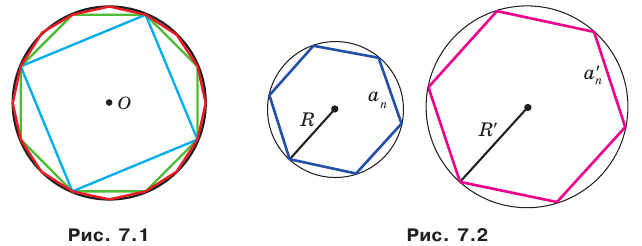 Рассмотрим два правильных
Рассмотрим два правильных 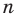 -угольника со сторонами
-угольника со сторонами 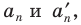 вписанных в окружности, радиусы которых равны
вписанных в окружности, радиусы которых равны 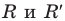 соответственно (рис. 7.2). Тогда их периметры
соответственно (рис. 7.2). Тогда их периметры 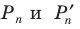 можно вычислить по формулам
можно вычислить по формулам
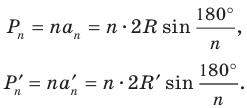
Отсюда
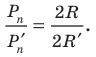
Это равенство справедливо при любом значении 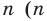 — натуральное число,
— натуральное число,  При неограниченном увеличении значения
При неограниченном увеличении значения 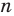 периметры
периметры  соответственно будут сколь угодно мало отличаться от длин
соответственно будут сколь угодно мало отличаться от длин 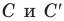 описанных окружностей. Тогда при неограниченном увеличении
описанных окружностей. Тогда при неограниченном увеличении  отношение
отношение 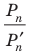 будет сколь угодно мало отличаться от отношения
будет сколь угодно мало отличаться от отношения 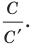 С учетом равенства
С учетом равенства  приходим к выводу, что число
приходим к выводу, что число 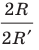 сколь угодно мало отличается от числа
сколь угодно мало отличается от числа 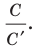
А это возможно только тогда, когда 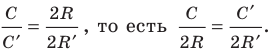
Последнее равенство означает, что для всех окружностей отношение длины окружности к диаметру является одним и тем же числом.
Из курса математики 6 класса вы знаете, что это число принято обозначать греческой буквой 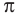 (читают: «пи»).
(читают: «пи»).
Из равенства 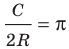 я получаем формулу для вычисления длины окружности:
я получаем формулу для вычисления длины окружности:
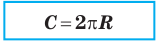
Число 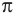 иррациональное, следовательно, его невозможно представить в виде конечной десятичной дроби. Обычно при решении задач в качестве приближенного значения
иррациональное, следовательно, его невозможно представить в виде конечной десятичной дроби. Обычно при решении задач в качестве приближенного значения 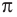 принимают число 3,14.
принимают число 3,14.
Великий древнегреческий ученый Архимед (III в. до н. э.), выразив через диаметр описанной окружности периметр правильного 96-угольника, установил, что 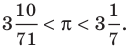 Отсюда и следует, что
Отсюда и следует, что 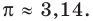
С помощью современных компьютеров и специальных программ можно вычислить число 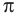 с огромной точностью. Приведем запись числа
с огромной точностью. Приведем запись числа 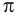 с 47 цифрами после запятой:
с 47 цифрами после запятой:
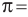 3,14159265358979323846264338327950288419716939937…. В 1989 г. число
3,14159265358979323846264338327950288419716939937…. В 1989 г. число 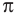 вычислили с точностью до 1 011 196 691 цифры после запятой. Этот факт был занесен в Книгу рекордов Гиннесса. Само число в книге не приведено, так как для этого понадобилось бы более тысячи страниц. В 2017 г. уже было вычислено более 22 триллионов знаков числа
вычислили с точностью до 1 011 196 691 цифры после запятой. Этот факт был занесен в Книгу рекордов Гиннесса. Само число в книге не приведено, так как для этого понадобилось бы более тысячи страниц. В 2017 г. уже было вычислено более 22 триллионов знаков числа 
Найдем формулу для вычисления длины дуги окружности с градусной мерой  Поскольку градусная мера всей окружности равна
Поскольку градусная мера всей окружности равна  то длина дуги в
то длина дуги в 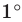 равна
равна 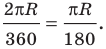 Тогда длину
Тогда длину  дуги в
дуги в  вычисляют по формуле
вычисляют по формуле
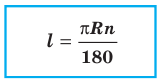
Выведем формулу для вычисления площади круга.
Обратимся снова к рисунку 7.1. Видим, что при увеличении количества сторон правильного 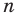 -угольника его площадь
-угольника его площадь 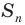 все меньше и меньше отличается от площади
все меньше и меньше отличается от площади  круга. При неограниченном увеличении количества сторон его площадь стремится к площади круга.
круга. При неограниченном увеличении количества сторон его площадь стремится к площади круга.
На рисунке 7.3 изображен фрагмент правильного  -угольника с центром в точке
-угольника с центром в точке  со стороной
со стороной  и радиусом описанной окружности, равным
и радиусом описанной окружности, равным 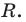 Опустим перпендикуляр
Опустим перпендикуляр 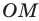 на сторону
на сторону 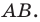 Имеем:
Имеем:
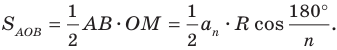
Поскольку радиусы, проведенные в вершины правильного 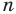 -угольника, разбивают его на
-угольника, разбивают его на 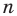 равных треугольников, то площадь
равных треугольников, то площадь 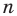 -угольника
-угольника  раз больше площади треугольника
раз больше площади треугольника 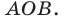 Тогда
Тогда 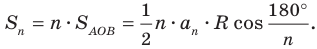
Отсюда
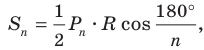 где
где  — периметр данного правильного
— периметр данного правильного 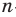 -угольника.
-угольника.
При неограниченном увеличении значения 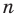 величина
величина 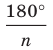 будет сколь угодно мало отличаться от
будет сколь угодно мало отличаться от 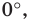 а следовательно,
а следовательно, 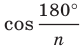 будет стремиться к 1. Периметр
будет стремиться к 1. Периметр  будет стремиться к длине
будет стремиться к длине  окружности, а площадь
окружности, а площадь  — к площади
— к площади 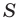 круга. Тогда с учетом равенства
круга. Тогда с учетом равенства  можно записать:
можно записать: 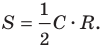
Из этого равенства получаем формулу для нахождения площади круга:
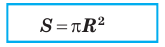
На рисунке 7.4 радиусы  делят круг на две части, закрашенные разными цветами. Каждую из этих частей вместе с радиусами
делят круг на две части, закрашенные разными цветами. Каждую из этих частей вместе с радиусами  называют круговым сектором или просто сектором.
называют круговым сектором или просто сектором.
Понятно, что круг радиуса 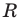 можно разделить на 360 равных секторов, каждый из которых будет содержать дугу в
можно разделить на 360 равных секторов, каждый из которых будет содержать дугу в 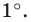 Площадь
Площадь 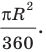 такого сектора равна.Тогда площадь
такого сектора равна.Тогда площадь  сектора, содержащего дугу окружности в
сектора, содержащего дугу окружности в  вычисляют по формуле:
вычисляют по формуле:
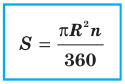
На рисунке 7.5 хорда 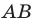 делит круг на две части, закрашенные разными цветами. Каждую из этих частей вместе с хордой
делит круг на две части, закрашенные разными цветами. Каждую из этих частей вместе с хордой 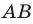 называют круговым сегментом или просто сегментом. Хорду
называют круговым сегментом или просто сегментом. Хорду 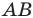 при этом называют основанием сегмента.
при этом называют основанием сегмента.
 Чтобы найти площадь сегмента, закрашенного розовым цветом (рис. 7.6), надо из площади сектора, содержащего хорду
Чтобы найти площадь сегмента, закрашенного розовым цветом (рис. 7.6), надо из площади сектора, содержащего хорду  вычесть площадь треугольника
вычесть площадь треугольника  (точка
(точка  — центр круга). Чтобы найти площадь сегмента, закрашенного голубым цветом, надо к площади сектора, не содержащего хорду
— центр круга). Чтобы найти площадь сегмента, закрашенного голубым цветом, надо к площади сектора, не содержащего хорду  прибавить площадь треугольника
прибавить площадь треугольника 
Если хорда  является диаметром круга, то она делит круг на два сегмента, которые называют полукругами. Площадь
является диаметром круга, то она делит круг на два сегмента, которые называют полукругами. Площадь  полукруга вычисляют по формуле
полукруга вычисляют по формуле 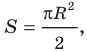 где
где 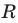 — радиус круга.
— радиус круга.
Пример №18
Длина дуги окружности, радиус которой 25 см, равна  см. Найдите градусную меру дуги.
см. Найдите градусную меру дуги.
Решение:
Из формулы  получаем
получаем 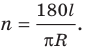 Следовательно искомая градусная мера
Следовательно искомая градусная мера 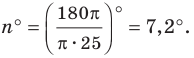
Ответ: 
Пример №19
В окружность с центром  радиус которой равен 8 см, вписан правильный восьмиугольник
радиус которой равен 8 см, вписан правильный восьмиугольник  (рис. 7.7). Найдите площади сектора и сегмента, содержащих дугу
(рис. 7.7). Найдите площади сектора и сегмента, содержащих дугу 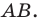
Решение:
Угол  — центральный угол правильного восьмиугольника, поэтому
— центральный угол правильного восьмиугольника, поэтому 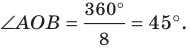
Тогда искомая площадь сектора равна 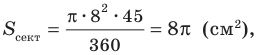 площадь сегмента:
площадь сегмента:
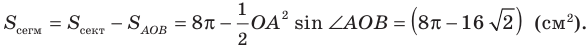
Ответ: 
Справочный материал
Правильный многоугольник
Многоугольник называют правильным, если у него все стороны равны и все углы равны.
Свойства правильного многоугольника
Правильный многоугольник является выпуклым многоугольником.
Любой правильный многоугольник является как вписанным в окружность, так и описанным около окружности, причем центры описанной и вписанной окружностей совпадают.
Формулы для нахождения радиусов описанной и вписанной окружностей правильного многоугольника

Длина окружности
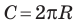
Длина дуги окружности в 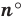
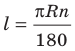
Площадь круга
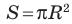
Площадь сектора, содержащего дугу окружности в 
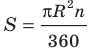
- Вписанные и описанные многоугольники
- Площадь прямоугольника
- Объем пространственных фигур
- Объёмы поверхностей геометрических тел
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии
- Многоугольник
- Площадь многоугольника
Download Article
Download Article
A regular polygon is a 2-dimensional convex figure with congruent sides and angles equal in measure.[1]
Many polygons, such as quadrilaterals or triangles have simple formulas for finding their areas, but if you’re working with a polygon that has more than four sides, then your best bet may be to use a formula that uses the shape’s apothem[2]
and perimeter. With a little bit of effort, you can find the area of regular polygons in just a few minutes.
-

1
Calculate the perimeter. The perimeter is the combined length of the outline of any two-dimensional figure. For a regular polygon, it can be calculated by multiplying the length of one side by the number of sides (n).[3]
-

2
Determine the apothem. The apothem of a regular polygon is the shortest distance from the center point to one of the sides, creating a right angle. This is a little trickier to calculate than the perimeter.[4]
- The formula for calculating the length of the apothem is this: the length of the side (s) divided by 2 times the tangent (tan) of 180 degrees divided by the number of sides (n).
Advertisement
-

3
Know the correct formula. The area of any regular polygon is given by the formula: Area = (a x p)/2, where a is the length of the apothem and p is the perimeter of the polygon.
-

4
Plug the values of a and p in the formula and get the area. As an example, let’s use a hexagon (6 sides) with a side (s) length of 10.[5]
- The perimeter is 6 x 10 (n x s), equal to 60 (so p = 60).
- The apothem is calculated by its own formula, by plugging in 6 and 10 for n and s. The result of 2tan(180/6) is 1.1547, and then 10 divided by 1.1547 is equal to 8.66.
- The area of the polygon is Area = a x p / 2, or 8.66 multiplied by 60 divided by 2. The solution is an area of 259.8 units.
- Note as well, there are no parenthesis in the “Area” equation, so 8.66 divided by 2 multiplied by 60, will give you the same result, just as 60 divided by 2 multiplied by 8.66 will give you the same result.
Advertisement
-

1
Understand that a regular polygon can be thought of as a collection of triangles. Each side represents the base of a triangle, and there are as many triangles in the polygon as there are sides. Each of the triangles are equal in base length, height, and area.[6]
-

2
Remember the formula for the area of a triangle. The area of any triangle is 1/2 times the length of the base (which, in the polygon, is the length of a side) multiplied by the height (which is the same as the apothem in regular polygon).[7]
-

3
See the similarities. Again, the formula for a regular polygon is 1/2 times the apothem multiplied by the perimeter. The perimeter is just the length of one side multiplied the by the number of sides (n); for a regular polygon, n also represents the number of triangles that make up the figure. The formula, then, is nothing more than the area of a triangle multiplied by the number of triangles in the polygon.[8]
Advertisement
Add New Question
-
Question
How do I find the perimeter of a regular polygon with one side being 5-2x and another being -4x+9?

Since a regular polygon has congruent sides (every side is equal to each other) you set up the equation 5-2x = -4x+9 then you solve for “x”. After solving for “x”, you substitute the answer you got from “x” back into the one of the expressions from one of the sides. You should get the answer of how many units one of the sides is. After that, just multiply that answer by how many sides the polygon has to get your perimeter.
-
Question
How do I find the perimeter of a nonagon with area of 28.8 and side length of 21?

The perimeter equals the side length times the number of sides. In this case, multiply 21 by 9 and you will get a perimeter of 189.
-
Question
What is the area of a polygon with sides of 12m, 11m, 3m, and 3m?

Since the given measurements of the sides best represents a trapezoid, you use the area of a trapezoid equation A=h*((b1+b2)*0.5) where A is the area, h is the height of the trapezoid, and where b1 is the top base and b2 is the bottom base. To find the height, you subtract b2 by b1, then divide it, then substitute that answer into “a” of the Pythagorean theorem a^2+b^2=c^2, where “c” equals the length of the side of your trapezoid which in this case is 3m. You solve for b in that equation to get your height. Once you got the measurement of the height of the trapezoid, you use the area of a trapezoid equation and substitute your answers in it to get your area.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If the drawing of your polygon has been separated into triangles, and one triangle’s area is labeled, then you do not need to know the apothem. Just take the area of that one triangle, and multiply by the number of sides in the original polygon.
Advertisement
Area Help
References
About This Article
Article SummaryX
To find the area of regular polygons, use the formula: area = (ap)/2, where a is the apothem and p is the perimeter. To find the apothem, divide the length of one side by 2 times the tangent of 180 degrees divided by the number of sides. To find the perimeter, multiply the length of one side by the total number of sides. Once you’ve found the apothem and the perimeter, plug them into the formula for area and solve. If you want to learn more about how finding the apothem works for calculating the area, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 804,495 times.
Reader Success Stories
-

“Thank you, this really helped me understand how the formula was actually created for my geometry test because I…” more
Did this article help you?
Найдём площадь правильного многоугольника через радиусы вписанной и описанной окружностей и через его сторону.
Любой правильный многоугольник вписан в окружность и описан около окружности. Центры вписанной и описанной окружностей совпадают и называются центром правильного многоугольника.
 Соединив центр правильного n-угольника
Соединив центр правильного n-угольника
![]()
со всеми его вершинами, получим n равнобедренных треугольников.
Основание каждого такого треугольника равно стороне многоугольника, боковые стороны равны радиусу описанной около многоугольника окружности угол при вершине — центральному углу правильного многоугольника
![]()
![]()
![]()
Так как площадь треугольника равна половине произведения его сторон на синус угла между ними,
![]()
Отсюда
![]()
Поскольку многоугольник состоит из n таких треугольников, формула площади правильного многоугольника через радиус описанной окружности:
![]()
 Проведём в треугольнике A1OA2 высоту OF. Её длина равна радиусу вписанной в правильный n-угольник окружности:
Проведём в треугольнике A1OA2 высоту OF. Её длина равна радиусу вписанной в правильный n-угольник окружности:
![]()
По свойству равнобедренного треугольника OF является также его биссектрисой и медианой:
![]()
![]()
Из прямоугольного треугольника A1OF по определению тангенса
![]()
откуда
![]()
Так как площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне,
![]()
![]()
Площадь
![]()
равна сумме n таких площадей.
Таким образом, формула площади правильного многоугольника через радиус вписанной окружности:
![]()
Из треугольника A1OF
![]()
Следовательно,
![]()
Поскольку многоугольник состоит из n равных треугольников, формула площади правильного многоугольника через его сторону:
![]()