2023-02-22
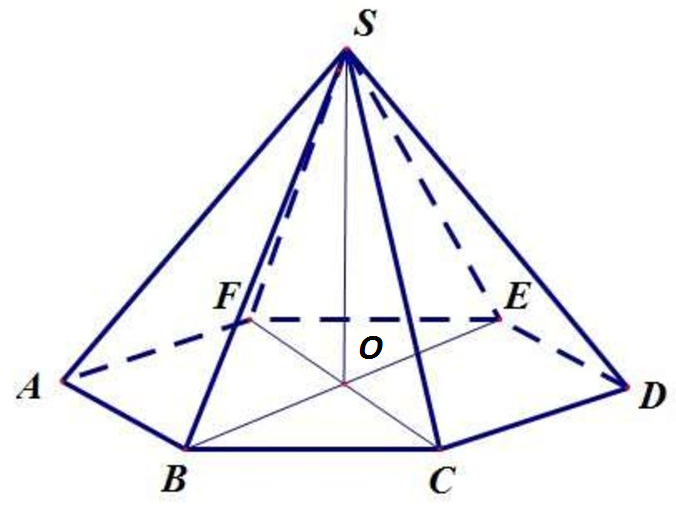
В правильной шестиугольной пирамиде с вершиной $S$ стороны основания $ABCDEF$ равны 6, а боковые рёбра равны 12. Точки $K$ и $M$ – середины рёбер и $SF$ и $SE$ соответственно.
а) Постройте сечение пирамиды плоскостью $BKM$
б) Найдите площадь полученного сечения.
Решение:
а) Поскольку $KMparallel EFparallel BC$, прямая $BC$, а значит, и точка $C$, лежат в секущей плоскости. Пусть $O$ – центр основания пирамиды, $P$ – точка пересечения её высоты $SO$ с отрезком $BM$, лежащим в секущей плоскости, а т.к. $O$ – середина диагонали $BE$ правильного шестиугольника, то $P$ – точка пересечения медиан треугольника $BSE$. Тогда $SP:PO=2:1$.
Прямая $KM$ параллельна плоскости $ASD$. т.к. она параллельна прямой $AD$, лежащей в этой плоскости. Проведённая через прямую $KM$ секущая плоскость проходит через точку $P$, лежащую в плоскости $ASD$, поэтому эти плоскости пересекаются по прямой, проходящей через точку $P$ параллельно $KM$.
Пусть эта прямая пересекает рёбра $SA$ и $SD$ в точках $L$ и $N$ соответственно. Тогда искомое сечение – шестиугольник $BLKMNC$. При этом $frac{SL}{LA}=frac{SN}{ND}=frac{SP}{PO}=2$.
б) Диагональ $LN$ шестиугольника $BLKMNC$ параллельна $AD$, поэтому треугольник $LSN$ подобен треугольнику $ASD$, причём коэффициент подобия равен $frac{SL}{SA}=frac{2}{3}$. Значит,
$LN=frac{2}{3}AD=frac{2}{3}cdot12=8.$
Диагональ $BM$ этого шестиугольника – медиана равностороннего треугольника со стороной $BL=12$, поэтому
$BM=12cdotfrac{sqrt{3}}{2}=6sqrt{3},~BP=frac{2}{3}BM=4sqrt{3}.$
Пусть $PH$ и $PQ$ – высоты равнобедренных трапеций $BLNC$ и $LKMN$ соответственно. Из прямоугольного треугольника $BHP$ находим, что
$PH=sqrt{BP^{2}-BH^{2}}=sqrt{48-9}=sqrt{39},~PQ=frac{1}{2}PH=frac{sqrt{39}}{2}.$
Следовательно,
$S_{BLKMNC}=S_{MLNC}+S_{LKMN}=frac{1}{2}(BC+LN)cdot PH+frac{1}{2}(LN+KM)cdot PQ=frac{1}{2}(6+8)cdotsqrt{39}+frac{1}{2}(8+3)cdotfrac{sqrt{39}}{2}=frac{39sqrt{39}}{4}.$
Как понять площадь сечения пирамиды? Например шестиугольной? Как найти? Помогите
Робеспьер
Ученик
(35),
закрыт
7 лет назад
Лучший ответ
Наталия
Высший разум
(363061)
7 лет назад
Для расчета площади правильной шестиугольной пирамиды применяется стандартная формула площади боковой поверхности шестиугольной пирамиды:
http:___//2mb.ru/matematika/geometriya/ploshhad-shestiugolnoj-piramidy/#ixzz3bozJMSDL убрать пробелы
Остальные ответы
Похожие вопросы
Условие
узнать площадь диагонального сечения правильной шестиугольной пирамиды. если длина стороны основания 12 см, а угол между боковым ребром и высотой пирамиды 30 градусов.
математика 10-11 класс
2567
Решение
★
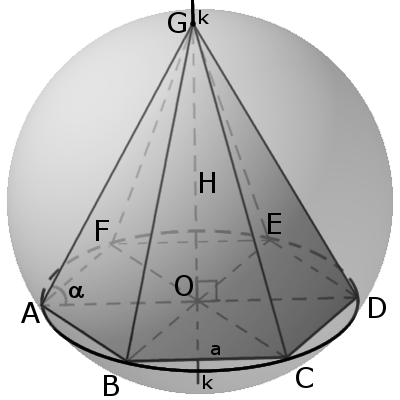
В правильном шестиугольнике АВСDEF:
АВ=ВС=СD=DE=EF=FA=OA=OB=OC=OD=OE=OF=12 cм
Значит, диагональ
ВЕ=ВО+ОЕ=12+12=24
В прямоугольном треугольнике SBO( SO⊥ пл. АВСDEF, а значит SO ⊥ BE):
SO=ВО*tg ∠ SBO=12*sqrt(3)
S(диаг.сеч)=S( Δ SBE)=(1/2)BE*SO=(1/2)*24*12sqrt(3) =144sqrt(3)
О т в е т. 144 sqrt(3)
Написать комментарий
Площадь сечения пирамиды
Пирамида — это многогранник, основанием которого является произвольный многоугольник, а боковые грани являются треугольниками, имеющие общую вершину. Основными математическими характеристиками пирамиды являются площадь основания и высота.
Сечение пирамиды — это изображение фигуры, образованной рассечением пирамиды плоскостью в поперечном или продольном направлении.
Формула для расчета площади основания пирамиды или сечения параллельного основанию:
S = a 2 , где
a — размер основания или сечения пирамиды.
Формула для расчета площади диагонального сечения пирамиды:
S = a * h / 2, где
a — основание пирамиды;
h — высота пирамиды.
Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади основания, бокового и диагонального сечения пирамиды, если известны основание пирамиды и высота правильной четырехугольной пирамиды. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения пирамиды (площадь диагонального сечения пирамиды, площадь бокового сечения пирамиды, площадь основания пирамиды и площадь сечения пирамиды параллельного основанию).
Как определить площадь сечения цилиндра, конуса, призмы и пирамиды? Формулы
На практике часто возникают задачи, которые требуют умения строить сечения геометрических фигур различной формы и находить площади сечений. В данной статье рассмотрим, как строятся важные сечения призмы, пирамиды, конуса и цилиндра, и как рассчитывать их площади.
Объемные фигуры
Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.

Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.
Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).
Цилиндр
Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.
Для этой фигуры существует три важных типа сечения:
- круглое;
- прямоугольное;
- эллиптическое.
Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.
Площадь круглого сечения рассчитывается по формуле:
Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:
Сечения конуса
Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.
Видов конических сечений существует несколько. Перечислим их:
- круглое;
- эллиптическое;
- параболическое;
- гиперболическое;
- треугольное.
Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.
Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:
Здесь z — это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z Понравилась статья? Поделись с друзьями:
Пирамида. Формулы и свойства пирамиды
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.
Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.
-
Формула площади правильной пирамиды
- 1. Общая формула
- 2. Площадь правильной треугольной пирамиды
- 3. Площадь правильной четырехугольной пирамиды
- 4. Площадь правильной шестиугольной пирамиды
Формула площади правильной пирамиды
1. Общая формула
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.
Sполн. = Sбок. + Sосн.
Боковой гранью правильной пирамиды является равнобедренный треугольник.
Площадь треугольника вычисляется по формулам:
1. Через длину основания (a) и высоту (h):
2. Через основание (a) и боковую сторону (b):
Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
2. Площадь правильной треугольной пирамиды
Основание: равносторонний треугольник.
L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.
3. Площадь правильной четырехугольной пирамиды
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 2aL |
 |
|
| полная | Sполн. = a2 + 2aL |
 |
microexcel.ru
4. Площадь правильной шестиугольной пирамиды
Основание: правильный шестиугольник