Онлайн калькулятор расчета площади поверхности профильной трубы
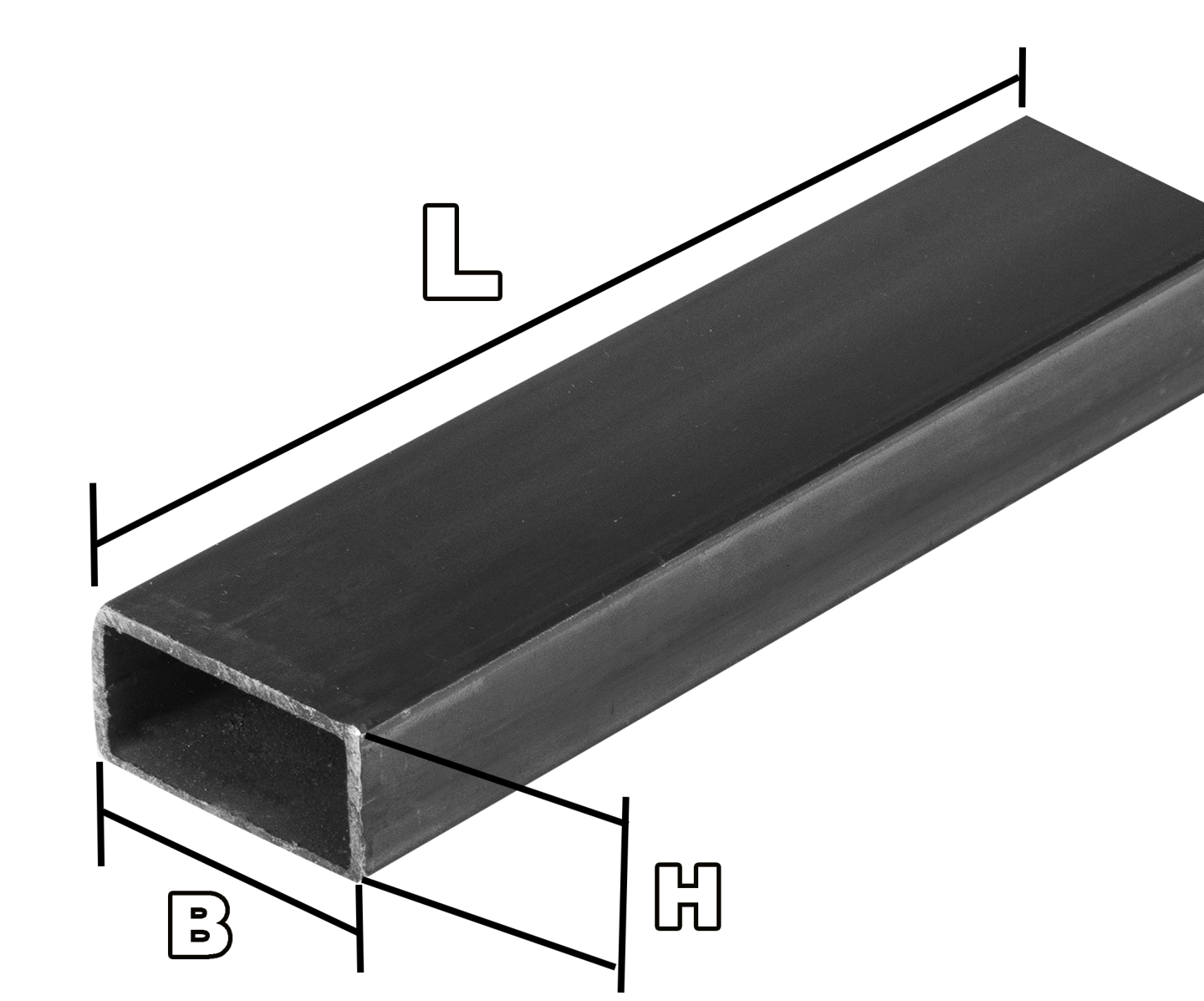
Длина профильной трубы
Высота профиля
Ширина профиля
Такой калькулятор может быть полезен для расчета площади окраски профилей или зачистки, чтобы примерно оценить стоимость работы и краски.
Формула
Площадь профильной трубы можно рассчитать по формуле:
(S = (B+H)*L*pi)
B – ширина прямоугольной трубы
H – высота прямоугольной трубы
L – длина трубы
(pi) – 3.14
Содержание:
Произвести расчет сечения трубы довольно просто, ведь для этого есть ряд стандартных формул, а также многочисленные калькуляторы и сервисы в интернете, которые могут выполнить ряд простых действий. В данном материале мы расскажем о том, как рассчитать площадь сечения трубы самостоятельно, ведь в некоторых случаях нужно учитывать ряд конструкционных особенностей трубопровода.

Формулы вычислений
При проведении вычислений нужно учитывать, что по существу трубы имеют форму цилиндра. Поэтому для нахождения площади их сечения можно воспользоваться геометрической формулой площади окружности. Зная внешний диаметр трубы и значение толщины его стенок, можно найти показатель внутреннего диаметра, который понадобится для вычислений.
Стандартная формула площади окружности такова:
S=π×R2, где
π – постоянное число, равное 3,14;
R – величина радиуса;
S – площадь сечения трубы, вычисленная для внутреннего диаметра.
Порядок расчета
Поскольку главная задача – это найти площадь проходного сечения трубы, основная формула будет несколько видоизменена.

В результате вычисления производятся так:
S=π×(D/2-N)2, где
D – значение внешнего сечения трубы;
N – толщина стенок.
Примите к сведению, что, чем больше знаков в числе π вы подставите в расчеты, тем точнее они будут.

Приведем числовой пример нахождения поперечного сечения трубы, с наружным диаметром в 1 метр (N). При этом стенки имеют толщину в 10 мм (D). Не вдаваясь в тонкости, примем число π равным 3,14.
Итак, расчеты выглядят следующим образом:
S=π×(D/2-N)2=3,14×(1/2-0,01)2=0,754 м2.
Физические характеристики труб
Стоит знать, что показатели площади поперечного сечения трубы напрямую влияют на скорость транспортировки газообразных и жидких веществ. Поэтому крайне важно заложить в проект трубы с правильным сечением. Кроме того, на выбор диаметра трубы будет влиять еще и рабочее давление в трубопроводе. Читайте также: “Как посчитать площадь трубы – способы и формулы расчета”.

Также в процессе проектирования трубопроводов стоит учитывать химические свойства рабочей среды, а также ее температурные показатели. Даже если вы знакомы с формулами, как найти площадь сечения трубы, стоит изучить дополнительный теоретический материал. Так, информация относительно требований к диаметрам трубопроводов под горячее и холодное водоснабжение, отопительные коммуникации или транспортировку газов, содержатся в специальной справочной литературе. Значение имеет также сам материал, из которого произведены трубы.
Выводы
Таким образом, определение площади сечения трубы является очень важным, однако, в процессе проектировки нужно обращать внимание на характеристики и особенности системы, материалы трубных изделий и их прочностные показатели.
Площадь поверхности квадратной трубы онлайн калькулятор.

Сторона “A” в миллиметрах.
Сторона “B” в миллиметрах.
(разделитель дробной части от целой – точка)
Расход краски грамм на м2.
Количество наносимых слоев краски.
Результаты:
(радиусом изгиба трубы пренебречь)
Площадь поверхности квадратной-профильной трубы в м2.
Количество краски для покраски трубы в гр.
Площадь профильной трубы.
Площадь Трубы 10×10
Площадь поперечного сечения = 100 мм2
Площадь поверхности одного метра =
0.04 м2
Площадь Трубы 10×15 (15×10)
Площадь поперечного сечения = 150 мм2
Площадь поверхности одного метра =
0.05 м2
Площадь Трубы 10×20 (20×10)
Площадь поперечного сечения = 200 мм2
Площадь поверхности одного метра =
0.06 м2
Площадь Трубы 10×25 (25×10)
Площадь поперечного сечения = 250 мм2
Площадь поверхности одного метра =
0.07 м2
Площадь Трубы 15×15
Площадь поперечного сечения = 225 мм2
Площадь поверхности одного метра =
0.06 м2
Площадь Трубы 20×20
Площадь поперечного сечения = 400 мм2
Площадь поверхности одного метра =
0.08 м2
Площадь Трубы 20×30 (30×20)
Площадь поперечного сечения = 600 мм2
Площадь поверхности одного метра =
0.1 м2
Площадь Трубы 20×40 (40×20)
Площадь поперечного сечения = 800 мм2
Площадь поверхности одного метра =
0.12 м2
Площадь Трубы 25×25
Площадь поперечного сечения = 625 мм2
Площадь поверхности одного метра =
0.1 м2
Площадь Трубы 25×40 (40×25)
Площадь поперечного сечения = 1000 мм2
Площадь поверхности одного метра =
0.13 м2
Труба профильная площадь окраски.
Площадь Трубы 28×25 (25×28)
Площадь поперечного сечения = 700 мм2
Площадь поверхности одного метра =
0.106 м2
Площадь Трубы 30×15 (15×30)
Площадь поперечного сечения = 450 мм2
Площадь поверхности одного метра =
0.09 м2
Площадь Трубы 30×20 (20×30)
Площадь поперечного сечения = 600 мм2
Площадь поверхности одного метра =
0.1 м2
Площадь Трубы 30×30
Площадь поперечного сечения = 900 мм2
Площадь поверхности одного метра =
0.12 м2
Площадь Трубы 40×40
Площадь поперечного сечения = 1600 мм2
Площадь поверхности одного метра =
0.16 м2
Площадь Трубы 50×20 (20×50)
Площадь поперечного сечения = 1000 мм2
Площадь поверхности одного метра =
0.14 м2
Площадь Трубы 50×25 (25×50)
Площадь поперечного сечения = 1250 мм2
Площадь поверхности одного метра =
0.15 м2
Площадь Трубы 50×30 (30×50)
Площадь поперечного сечения = 1500 мм2
Площадь поверхности одного метра =
0.16 м2
Площадь Трубы 50×40 (40×50)
Площадь поперечного сечения = 2000 мм2
Площадь поверхности одного метра =
0.18 м2
Площадь Трубы 50×50
Площадь поперечного сечения = 2500 мм2
Площадь поверхности одного метра =
0.2 м2
Площадь покраски профильной трубы.
Площадь Трубы 60×30 (30×60)
Площадь поперечного сечения = 1800 мм2
Площадь поверхности одного метра =
0.18 м2
Площадь Трубы 60×40 (40×60)
Площадь поперечного сечения = 2400 мм2
Площадь поверхности одного метра =
0.2 м2
Площадь Трубы 60×60
Площадь поперечного сечения = 3600 мм2
Площадь поверхности одного метра =
0.24 м2
Площадь Трубы 70×70
Площадь поперечного сечения = 4900 мм2
Площадь поверхности одного метра =
0.28 м2
Площадь Трубы 80×40 (40×80)
Площадь поперечного сечения = 3200 мм2
Площадь поверхности одного метра =
0.24 м2
Площадь Трубы 80×60 (60×80)
Площадь поперечного сечения = 4800 мм2
Площадь поверхности одного метра =
0.28 м2
Площадь Трубы 80×80
Площадь поперечного сечения = 6400 мм2
Площадь поверхности одного метра =
0.32 м2
Площадь Трубы 100×50 (50×100)
Площадь поперечного сечения = 5000 мм2
Площадь поверхности одного метра =
0.3 м2
Площадь Трубы 100×60 (60×100)
Площадь поперечного сечения = 6000 мм2
Площадь поверхности одного метра =
0.32 м2
Площадь Трубы 100×80 (80×100)
Площадь поперечного сечения = 8000 мм2
Площадь поверхности одного метра =
0.36 м2
Площадь профильной трубы под окраску.
Площадь Трубы 100×100
Площадь поперечного сечения = 10000 мм2
Площадь поверхности одного метра =
0.4 м2
Площадь Трубы 120×60 (60×120)
Площадь поперечного сечения = 7200 мм2
Площадь поверхности одного метра =
0.36 м2
Площадь Трубы 120×80 (80×120)
Площадь поперечного сечения = 9600 мм2
Площадь поверхности одного метра =
0.4 м2
Площадь Трубы 120×120
Площадь поперечного сечения = 14400 мм2
Площадь поверхности одного метра =
0.48 м2
Площадь Трубы 140×60 (60×140)
Площадь поперечного сечения = 8400 мм2
Площадь поверхности одного метра =
0.4 м2
Площадь Трубы 140×100 (100×140)
Площадь поперечного сечения = 14000 мм2
Площадь поверхности одного метра =
0.48 м2
Площадь Трубы 140×140
Площадь поперечного сечения = 19600 мм2
Площадь поверхности одного метра =
0.56 м2
Площадь Трубы 150×100 (100×150)
Площадь поперечного сечения = 15000 мм2
Площадь поверхности одного метра =
0.5 м2
Площадь Трубы 150×150
Площадь поперечного сечения = 22500 мм2
Площадь поверхности одного метра =
0.6 м2
Площадь Трубы 160×80 (80×160)
Площадь поперечного сечения = 12800 мм2
Площадь поверхности одного метра =
0.48 м2
Площадь поверхности профильной трубы.
Площадь Трубы 160×120 (120×160)
Площадь поперечного сечения = 19200 мм2
Площадь поверхности одного метра =
0.56 м2
Площадь Трубы 160×160
Площадь поперечного сечения = 25600 мм2
Площадь поверхности одного метра =
0.64 м2
Площадь Трубы 180×100 (100×180)
Площадь поперечного сечения = 18000 мм2
Площадь поверхности одного метра =
0.56 м2
Площадь Трубы 180×180
Площадь поперечного сечения = 32400 мм2
Площадь поверхности одного метра =
0.72 м2
Площадь Трубы 200×120 (120×200)
Площадь поперечного сечения = 24000 мм2
Площадь поверхности одного метра =
0.64 м2
Площадь Трубы 200×160 (160×200)
Площадь поперечного сечения = 32000 мм2
Площадь поверхности одного метра =
0.72 м2
Площадь Трубы 200×200
Площадь поперечного сечения = 40000 мм2
Площадь поверхности одного метра =
0.8 м2
Площадь Трубы 250×250
Площадь поперечного сечения = 62500 мм2
Площадь поверхности одного метра =
1 м2
Площадь Трубы 250×300 (300×250)
Площадь поперечного сечения = 75000 мм2
Площадь поверхности одного метра =
1.1 м2
Площадь Трубы 300×300
Площадь поперечного сечения = 90000 мм2
Площадь поверхности одного метра =
1.2 м2
Формулы вычислений
При проведении вычислений нужно учитывать, что по существу трубы имеют форму цилиндра. Поэтому для нахождения площади их сечения можно воспользоваться геометрической формулой площади окружности. Зная внешний диаметр трубы и значение толщины его стенок, можно найти показатель внутреннего диаметра, который понадобится для вычислений.
Стандартная формула площади окружности такова:
S=π×R2, где
π – постоянное число, равное 3,14;
R – величина радиуса;
S – площадь сечения трубы, вычисленная для внутреннего диаметра.
Объемные фигуры
Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.
Вам будет интересно:Что значит слыть: толкование, синонимы
Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.
Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).
Определение сечения проводника на вводе

Подбор сечения осуществляется так, чтобы допустимый ток жил за длительный период был больше номинала автомата. Например, в доме на ввод пущен медный трехжильный проводник ВВГнг, уложенный открытым способом. Оптимальное сечение – 4 мм2, поэтому понадобится материал ВВГнг 3х4.
После этого высчитывается показатель условного тока отключения для автомата с номиналом 25 А: 1,45х25=36,25 А. У кабеля с площадью сечения 4 мм2 параметры длительно допустимого тока 35 А, условного – 36,25 А. В данном случае лучше взять вводный проводник из меди сечением 6 мм2 и допустимым предельным током 42 А.
Сечение проводов в домах старой застройки и предельная нагрузка
В многоэтажках советского периода используется алюминиевая проводка. С учетом правильного соединения узлов в распредкоробе, качества изоляции и надежности контактов соединения она прослужит от 10 до 30 лет.
При необходимости подключения техники с большой энергоемкостью в домах с проводкой из алюминия на основе мощности потребления подбирается сечение и диаметр жил. Все данные указаны в таблице.
| Ток, А | Максимальная мощность, ВА | Диаметр кабеля, мм | Сечение кабеля, мм2 |
| 14 | 3000 | 1,6 | 2 |
| 16 | 3500 | 1,8 | 2,5 |
| 18 | 4000 | 2 | 3 |
| 21 | 4600 | 2,3 | 4 |
| 24 | 5300 | 2,5 | 5 |
| 26 | 5700 | 2,7 | 6 |
| 31 | 6800 | 3,2 | 8 |
| 38 | 8400 | 3,6 | 10 |
Сечения призмы
Призма — это большой класс фигур, которые характеризуются наличием двух одинаковых параллельных друг другу многоугольных оснований, соединенных параллелограммами. Любое сечение призмы — это многоугольник. В виду разнообразия рассматриваемых фигур (наклонные, прямые, n-угольные, правильные, вогнутые призмы) велико и разнообразие их сечений. Далее рассмотрим лишь некоторые частные случаи.

Если секущая плоскость параллельна основанию, то площадь сечения призмы будет равна площади этого основания.
Если плоскость проходит через геометрические центры двух оснований, то есть является параллельной боковым ребрам фигуры, тогда в сечении образуется параллелограмм. В случае прямых и правильных призм рассматриваемый вид сечения будет представлять собой прямоугольник.
Вычисление сечения провода для линии розеток

- материал провода и способ укладки – трехжильный ВВГнг-кабель из меди, спрятанный в стене;
- особенности сечения – оптимальная величина составляет 1,5 мм2, т.е. понадобится кабель 3х1,5;
- использование розетки. Если подключается только машинка-автомат, характеристик будет достаточно;
- система защиты – автомат, номинальный ток которого 10 А.
Для двойных розеток применяется кабель из меди с сечением 2,5 мм2 и автомат номиналом 16 А.
Сечения конуса
Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:
- круглое;
- эллиптическое;
- параболическое;
- гиперболическое;
- треугольное.
Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.
Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:
S1 = pi*r2*z2/h2
Здесь z — это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z
Треугольное получается, когда плоскость пересекает фигуру по ее оси вращения. Формой получившегося сечения будет равнобедренный треугольник, сторонами которого являются диаметр основания и две образующие конуса. Как находить площадь сечения треугольного? Ответом на этот вопрос будет следующая формула:
S2 = r*h
Это равенство получается, если применить формулу для площади произвольного треугольника через длину его основания и высоту.
Виды цилиндра
Виды цилиндра зависят от того, под каким углом пересекаются образующие и основания нашего тела.
Если угол равен 90 градусам, то получим, так называемый, прямой цилиндр. У него есть ось симметрии – это перпендикуляр, соединяющий центры его оснований.
Если угол другой, то цилиндр называется наклонным.
Если форма основания – гипербола, то цилиндр гиперболический, если парабола — параболический, если эллипс — эллиптический, если круг — круговой.
Если основания цилиндра не параллельны, то он называется косым.
Порядок расчета
Поскольку главная задача – это найти площадь проходного сечения трубы, основная формула будет несколько видоизменена.

В результате вычисления производятся так:
S=π×(D/2-N)2, где
D – значение внешнего сечения трубы;
N – толщина стенок.
Примите к сведению, что, чем больше знаков в числе π вы подставите в расчеты, тем точнее они будут.

Приведем числовой пример нахождения поперечного сечения трубы, с наружным диаметром в 1 метр (N). При этом стенки имеют толщину в 10 мм (D). Не вдаваясь в тонкости, примем число π равным 3,14.
Итак, расчеты выглядят следующим образом:
S=π×(D/2-N)2=3,14×(1/2-0,01)2=0,754 м2.
Площадь поперечного сечения
В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.
Формулы для расчета площади основных фигур.
Пример: Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением. Для расчета общей площади, сложное сечение раскладывается на простые фигуры:
Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто. В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:
A=A1+A2+A3-A4
Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м2, см2 или мм2.
Площадь составного сечения
Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым. Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.
Эти сечения сами по себе тоже являются сложными. Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.
В результате сложив все составляющие профили, получим площадь всего сечения.
Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.
Расчет сечения многожильного проводника

- Находится показатель площади сечения у одной жилы.
- Пересчитываются кабельные жилы.
- Количество умножается на поперечное сечение одной жилы.
При подключении многожильного проводника его концы обжимаются специальной гильзой с использованием обжимных клещей.
Общие сведения
Площадь — это величина геометрической фигуры в двумерном пространстве. Она используется в математике, медицине, инженерных и других науках, например, в вычислении поперечного сечения клеток, атомов, или труб, таких как кровеносные сосуды или водопроводные трубы. В географии площадь используются для сравнения размеров городов, озер, стран и других географических объектов. При расчетах плотности населения также используется площадь. Плотность населения определяется как количество людей на единицу площади.
Читать также: Как правильно паять провода от наушников
Цилиндр
Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.

Для этой фигуры существует три важных типа сечения:
- круглое;
- прямоугольное;
- эллиптическое.
Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.
Площадь круглого сечения рассчитывается по формуле:
S1 = pi*r2
Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:
S2 = 2*r*h
Порядок расчета
Поскольку главная задача – это найти площадь проходного сечения трубы, основная формула будет несколько видоизменена.

В результате вычисления производятся так:
S=π×(D/2-N)2, где
D – значение внешнего сечения трубы;
N – толщина стенок.
Примите к сведению, что, чем больше знаков в числе π вы подставите в расчеты, тем точнее они будут.

Приведем числовой пример нахождения поперечного сечения трубы, с наружным диаметром в 1 метр (N). При этом стенки имеют толщину в 10 мм (D). Не вдаваясь в тонкости, примем число π равным 3,14.
Итак, расчеты выглядят следующим образом:
S=π×(D/2-N)2=3,14×(1/2-0,01)2=0,754 м2.
Цилиндр
Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.

Для этой фигуры существует три важных типа сечения:
- круглое;
- прямоугольное;
- эллиптическое.
Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.
Площадь круглого сечения рассчитывается по формуле:
S1 = pi*r2
Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:
S2 = 2*r*h
Сечения конуса
Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:
- круглое;
- эллиптическое;
- параболическое;
- гиперболическое;
- треугольное.
Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.
Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:
S1 = pi*r2*z2/h2
Здесь z — это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z
Треугольное получается, когда плоскость пересекает фигуру по ее оси вращения. Формой получившегося сечения будет равнобедренный треугольник, сторонами которого являются диаметр основания и две образующие конуса. Как находить площадь сечения треугольного? Ответом на этот вопрос будет следующая формула:
S2 = r*h
Это равенство получается, если применить формулу для площади произвольного треугольника через длину его основания и высоту.
Расчет сечения многожильного проводника

- Находится показатель площади сечения у одной жилы.
- Пересчитываются кабельные жилы.
- Количество умножается на поперечное сечение одной жилы.
При подключении многожильного проводника его концы обжимаются специальной гильзой с использованием обжимных клещей.
Выбор по таблице
Зная диаметр провода, можно определить его сечение по готовой таблице зависимости. Таблица расчета сечения кабеля по диаметру жилы выглядит таким образом:
| Диаметр проводника, мм | Сечение проводника, мм2 |
| 0.8 | 0.5 |
| 1 | 0.75 |
| 1.1 | 1 |
| 1.2 | 1.2 |
| 1.4 | 1.5 |
| 1.6 | 2 |
| 1.8 | 2.5 |
| 2 | 3 |
| 2.3 | 4 |
| 2.5 | 5 |
| 2.8 | 6 |
| 3.2 | 8 |
| 3.6 | 10 |
| 4.5 | 16 |
Когда сечение известно, можно определить значения допустимых мощности и тока для медного или алюминиевого провода. Таким образом удастся выяснить, на какие параметры нагрузки рассчитана токопроводящая жила. Для этого понадобится таблица зависимости сечения от максимального тока и мощности.
Перевод ватт в киловатты
Чтобы правильно воспользоваться таблицей зависимости сечения провода от мощности, важно правильно перевести ватты в киловатты.
1 киловатт = 1000 ватт. Соответственно, чтобы получить значение в киловаттах, мощность в ваттах необходимо разделить на 1000. Например, 4300 Вт = 4,3 кВт.

Формулы вычислений
При проведении вычислений нужно учитывать, что по существу трубы имеют форму цилиндра. Поэтому для нахождения площади их сечения можно воспользоваться геометрической формулой площади окружности. Зная внешний диаметр трубы и значение толщины его стенок, можно найти показатель внутреннего диаметра, который понадобится для вычислений.
Стандартная формула площади окружности такова:
S=π×R2, где
π – постоянное число, равное 3,14;
R – величина радиуса;
S – площадь сечения трубы, вычисленная для внутреннего диаметра.
Как рассчитать параметры труб
При строительстве и обустройстве дома трубы не всегда используются для транспортировки жидкостей или газов.
Часто они выступают как строительный материал — для создания каркаса различных построек, опор для навесов и т.д. При определении параметров систем и сооружений необходимо высчитать разные характеристики ее составляющих.
В данном случае сам процесс называют расчет трубы, а включает он в себя как измерения, так и вычисления.
Для чего нужны расчеты параметров труб
В современном строительстве используются не только стальные или оцинкованные трубы. Выбор уже довольно широк — ПВХ, полиэтилен (ПНД и ПВД), полипропилен, металлопластк, гофрированная нержавейка.
Они хороши тем, что имеют не такую большую массу, как стальные аналоги. Тем не менее, при транспортировке полимерных изделий в больших объемах знать их массу желательно — чтобы понять, какая машина нужна.
Вес металлических труб еще важнее — доставку считают по тоннажу. Так что этот параметр желательно контролировать.
То, что нельзя измерить, можно рассчитать
Знать площадь наружной поверхности трубы надо для закупки краски и теплоизоляционных материалов. Красят только стальные изделия, ведь они подвержены коррозии в отличие от полимерных. Вот и приходится защищать поверхность от воздействия агрессивных сред.
Используют их чаще для строительства заборов, каркасов для хозпостроек (гаражей, сараев, беседок, бытовок), так что условия эксплуатации — тяжелы, защита необходима, потому все каркасы требуют окраски.
Вот тут и потребуется площадь окрашиваемой поверхности — наружная площадь трубы.
При сооружении системы водоснабжения частного дома или дачи, трубы прокладывают от источника воды (колодца или скважины) до дома — под землей.
И все равно, чтобы они не замерзли, требуется утепление. Рассчитать количество утеплителя можно зная площадь наружной поверхности трубопровода.
Только в этом случае надо брать материал с солидным запасом — стыки должны перекрываться с солидным запасом.
Сечение трубы необходимо для определения пропускной способности — сможет ли данное изделие провести требуемое количество жидкости или газа. Этот же параметр часто нужен при выборе диаметра труб для отопления и водопровода, расчета производительности насоса и т.д.
Внутренний и наружный диаметр, толщина стенки, радиус
Трубы — специфический продукт. Они имеют внутренний и наружный диаметр, так как стенка у них толстая, ее толщина зависит от типа трубы и материала из которого она изготовлена. В технических характеристиках чаще указывают наружный диаметр и толщину стенки.
Внутренний и наружный диаметр трубы, толщина стенки
Имея эти два значения, легко высчитать внутренний диаметр — от наружного отнять удвоенную толщину стенки: d = D — 2*S. Если у вас наружный диаметр 32 мм, толщина стенки 3 мм, то внутренний диаметр будет: 32 мм — 2 * 3 мм = 26 мм.
Если же наоборот, имеется внутренний диаметр и толщина стенки, а нужен наружный — к имеющемуся значению добавляем удвоенную толщину стеки.
С радиусами (обозначаются буквой R) еще проще — это половина от диаметра: R = 1/2 D. Например, найдем радиус трубы диаметром 32 мм. Просто 32 делим на два, получаем 16 мм.
Измерения штангенциркулем более точные
Что делать, если технических данных трубы нет? Измерять. Если особая точность не нужна, подойдет и обычная линейка, для более точных измерений лучше использовать штангенциркуль.
Расчет площади поверхности трубы
Труба представляет собой очень длинный цилиндр, и площадь поверхность трубы рассчитывается как площадь цилиндра. Для вычислений потребуется радиус (внутренний или наружный — зависит от того, какую поверхность вам надо рассчитать) и длина отрезка, который вам необходим.
Формула расчета боковой поверхности трубы
Чтобы найти боковую площадь цилиндра, перемножаем радиус и длину, полученное значение умножаем на два, а потом — на число «Пи», получаем искомую величину. При желании можно рассчитать поверхность одного метра, ее потом можно умножать на нужную длину.
Для примера рассчитаем наружную поверхность куска трубы длиной 5 метров, с диаметром 12 см. Для начала высчитаем диаметр: делим диаметр на 2, получаем 6 см.
Теперь все величины надо привести к одним единицам измерения. Так как площадь считается в квадратных метрах, то сантиметры переводим в метры. 6 см = 0,06 м.
Дальше подставляем все в формулу: S = 2 * 3,14 * 0,06 * 5 = 1,884 м2. Если округлить, получится 1,9 м2.
Расчет веса
С расчетом веса трубы все просто: надо знать, сколько весит погонный метр, затем эту величину умножить на длину в метрах.
Вес круглых стальных труб есть в справочниках, так как этот вид металлопроката стандартизован. Масса одного погонного метра зависит от диаметра и толщины стенки.
Один момент: стандартный вес дан для стали плотностью 7,85 г/см2 — это тот вид, который рекомендован ГОСТом.
Таблица веса круглых стальных труб
В таблице Д — наружный диаметр, условный проход — внутренний диаметр, И еще один важный момент: указана масса обычных стального проката, оцинкованные на 3% тяжелее.
Таблица веса профилированной трубы квадратного сечения
Как высчитать площадь поперечного сечения
Формула нахождения площади сечения круглой трубы
Если труба круглая, площадь сечения считать надо по формуле площади круга: S = π*R2. Где R — радиус (внутренний), π — 3,14. Итого, надо возвести радиус в квадрат и умножить его на 3,14.
Например, площадь сечения трубы диаметром 90 мм. Находим радиус — 90 мм / 2 = 45 мм. В сантиметрах это 4,5 см. Возводим в квадрат: 4,5 * 4,5 = 2,025 см2, подставляем в формулу S = 2 * 20,25 см2 = 40,5 см2.
Сечения призмы
Призма — это большой класс фигур, которые характеризуются наличием двух одинаковых параллельных друг другу многоугольных оснований, соединенных параллелограммами. Любое сечение призмы — это многоугольник. В виду разнообразия рассматриваемых фигур (наклонные, прямые, n-угольные, правильные, вогнутые призмы) велико и разнообразие их сечений. Далее рассмотрим лишь некоторые частные случаи.

Если секущая плоскость параллельна основанию, то площадь сечения призмы будет равна площади этого основания.
Если плоскость проходит через геометрические центры двух оснований, то есть является параллельной боковым ребрам фигуры, тогда в сечении образуется параллелограмм. В случае прямых и правильных призм рассматриваемый вид сечения будет представлять собой прямоугольник.
Объемные фигуры
Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.
Вам будет интересно:Что значит слыть: толкование, синонимы
Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.
Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).
Площадь поперечного сечения
В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.
Формулы для расчета площади основных фигур.
Пример: Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением. Для расчета общей площади, сложное сечение раскладывается на простые фигуры:
Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто. В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:
A=A1+A2+A3-A4
Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м2, см2 или мм2.
Площадь составного сечения
Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым. Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.
Эти сечения сами по себе тоже являются сложными. Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.
В результате сложив все составляющие профили, получим площадь всего сечения.
Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.
