Площадь сечения треугольника
Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Основными математическими характеристиками треугольника являются длины сторон и высота.
Сечение треугольника – это изображение фигуры, образованной рассечением треугольника плоскостью в поперечном направлении.

Формула для расчета площади сечения треугольника:
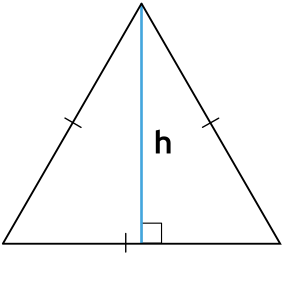
a – основание треугольника;
h – высота треугольника.
Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади сечения треугольника (осевого сечения), если известны основание треугольника и высота. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения треугольника (площадь осевого сечения треугольника, площадь сечения прямоугольного треугольника, площадь сечения равнобедренного треугольника).
Как найти площадь треугольника
О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
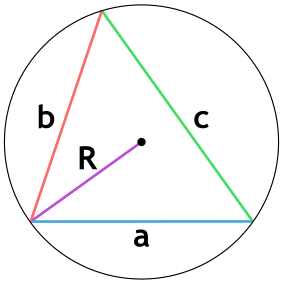
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
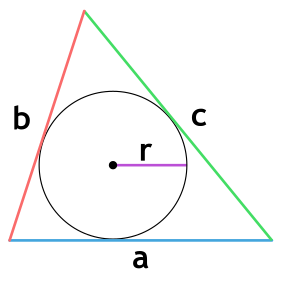
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
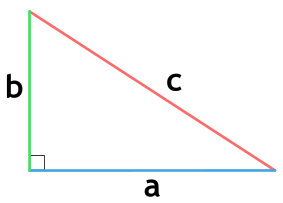
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
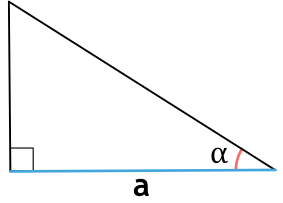
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
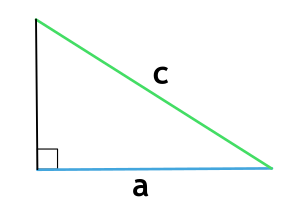
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
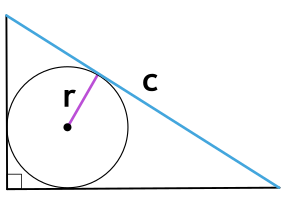
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/ploshad-treugolnika
http://mozgan.ru/Geometry/AreaTriangle
[/spoiler]
Как найти площадь равностороннего треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти площадь равностороннего треугольника
Чтобы найти площадь равностороннего (правильного, равноугольного) треугольника воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
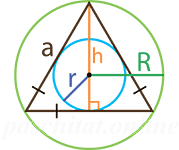
Чтобы вычислить площадь равностороннего треугольника вам нужно знать следующие параметры (либо-либо):
- длину равных сторон (a)
- высоту (h)
- радиус описанной окружности (R)
- радиус вписанной окружности (r)
- периметр треугольника (P)
Введите их в соответствующие поля и узнаете площадь равностороннего треугольника (S).
Как посчитать площадь равностороннего треугольника зная длину равных сторон
Чему равна площадь равностороннего треугольника если длина стороны
a =
?
Ответ:
S =
0
Какова площадь равностороннего треугольника (S) если известна длина сторон (a)?
Формула
S =√3/4 ⋅ a²
Пример
Если сторона a = 2 см, то:
S = √3/4 ⋅ 2² = 1.732/4 ⋅ 4 ≈ 1.732 см2
Как посчитать площадь равностороннего треугольника зная его высоту
Чему равна площадь равностороннего треугольника если его
высота h =
?
Ответ:
S =
0
Какова площадь равностороннего треугольника (S) если известна его высота (h)?
Формула
S =h² / √3
Пример
Если высота h = 3 см, то:
S = 3²/√3= 9/1.732 ≈ 5.19 см2
Как посчитать площадь равностороннего треугольника зная радиус описанной окружности
Чему равна площадь равностороннего треугольника если радиус описанной окружности
R =
?
Ответ:
S =
0
Какова площадь равностороннего треугольника (S) если известен радиус описанной окружности (R)?
Формула
S =3⋅√3/4 ⋅ R²
Пример
Если радиус описанной окружности R = 4 см, то:
S = 3 ⋅ √3/4 ⋅ 4² = 3 ⋅ 1.732/4 ⋅ 16 = 1.299 ⋅ 16 ≈ 20.784 см2
Как посчитать площадь равностороннего треугольника зная радиус вписанной окружности
Чему равна площадь равностороннего треугольника если радиус вписанной окружности
r =
?
Ответ:
S =
0
Какова площадь равностороннего треугольника (S) если известен радиус вписанной окружности (r)?
Формула
S =3⋅√3 ⋅ r²
Пример
Если радиус вписанной окружности r = 1 см, то:
S = 3⋅√3 ⋅ 1² = 3 ⋅ 1.732 ⋅ 1 ≈ 5.196 см2
Как посчитать площадь равностороннего треугольника зная его периметр
Чему равна площадь равностороннего треугольника если его периметр
P =
?
Ответ:
S =
0
Какова площадь равностороннего треугольника (S) если известен его периметр (P)?
Формула
S =√3/36 ⋅ P²
Пример
Если периметр P = 8 см, то:
S = √3/36 ⋅ 8² = 1.732/36 ⋅ 64 ≈ 3 см2
См. также

{S = dfrac{1}{2} cdot a cdot h}
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника – равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.
- Калькулятор площади треугольника
- Площадь треугольника
- через основание и высоту
- через две стороны и угол между ними
- через сторону и два прилежащих угла
- через радиус описанной окружности и 3 стороны
- через радиус вписанной окружности и 3 стороны
- по формуле Герона
- Площадь прямоугольного треугольника
- через катеты
- через гипотенузу и прилежащий угол
- через катет и прилежащий угол
- через радиус вписанной окружности и гипотенузу
- через вписанную окружность
- по формуле Герона
- через катет и гипотенузу
- Площадь равнобедренного треугольника
- через основание и сторону
- через основание, боковую сторону и угол
- через основание и высоту
- через боковые стороны и угол между ними
- через основание и угол между боковыми сторонами
- Площадь равностороннего треугольника
- через сторону
- через высоту
- через радиус описанной окружности
- через радиус вписанной окружности
- Примеры задач
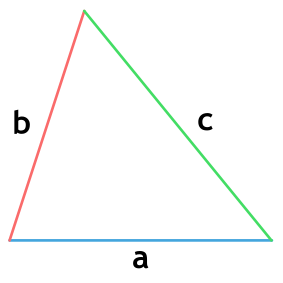
Площадь треугольника
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
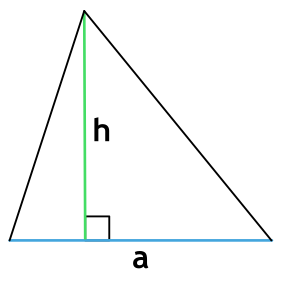
Площадь треугольника через основание и высоту
{S = dfrac{1}{2} cdot a cdot h}
a – длина основания
h – высота, проведенная к основанию
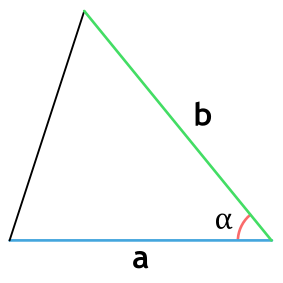
Площадь треугольника через две стороны и угол между ними
{S = dfrac{1}{2} cdot a cdot b cdot sin(alpha)}
a и b – стороны треугольника
α – угол между сторонами a и b
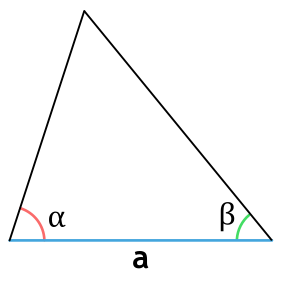
Площадь треугольника через сторону и два прилежащих угла
{S = dfrac{a^2}{2} cdot dfrac{sin{(alpha)} cdot sin{(beta)}}{sin{(gamma)}}}
{gamma = 180 – (alpha + beta)}
a – сторона треугольника
α и β – прилежащие к стороне a углы
Площадь треугольника через радиус описанной окружности и 3 стороны
{S = dfrac{a cdot b cdot c}{4 cdot R}}
a, b и c – стороны треугольника
R – радиус описанной окружности
Площадь треугольника через радиус вписанной окружности и 3 стороны
{S = r cdot dfrac{a + b + c}{2}}
a, b и c – стороны треугольника
r – радиус вписанной окружности
Площадь треугольника по формуле Герона
{S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника
Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).
Площадь прямоугольного треугольника через катеты
{S = dfrac{1}{2} cdot a cdot b}
a и b – стороны треугольника
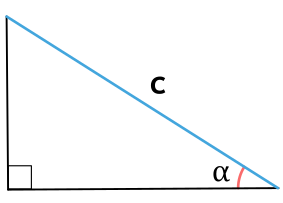
Площадь прямоугольного треугольника через гипотенузу и прилежащий угол
{S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)}}
c – гипотенуза прямоугольного треугольника
α – прилежащий к гипотенузе c угол
Площадь прямоугольного треугольника через катет и прилежащий угол
{S = dfrac{1}{2} cdot a^2 cdot tg{(alpha)}}
a – катет прямоугольного треугольника
α – прилежащий к катету a угол
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
{S = r cdot (r+c)}
r – радиус вписанной окружности
c – гипотенуза прямоугольного треугольника
Площадь прямоугольного треугольника через вписанную окружность
{S = c_1 cdot c_2}
с1 и с2 – отрезки, полученные делением гипотенузы точкой касания окружности
Площадь прямоугольного треугольника по формуле Герона
{S = (p-a) cdot (p-b)}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника через катет и гипотенузу
{S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2}}
a – катет прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
Площадь равнобедренного треугольника
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
Площадь равнобедренного треугольника через основание и сторону
{S = dfrac{b}{4} sqrt{4a^2 – b^2}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
Площадь равнобедренного треугольника через основание, сторону и угол
{S = dfrac{1}{2} cdot a cdot b cdot sin{(alpha)}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
α – угол между основанием и боковой стороной
Площадь равнобедренного треугольника через основание и высоту
{S = dfrac{1}{2} cdot b cdot h}
b – основание равнобедренного треугольника
h – высота, проведенная к основанию равнобедренного треугольника
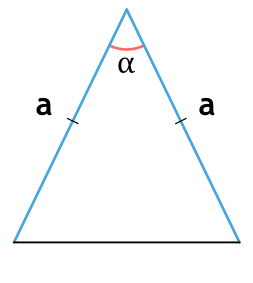
Площадь равнобедренного треугольника через боковые стороны и угол между ними
{S = dfrac{1}{2} cdot a^2 cdot sin(alpha)}
a – боковые стороны равнобедренного треугольника
α – угол между боковыми сторонами
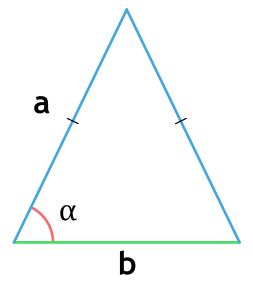
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами
{S = dfrac{b^2}{4 cdot tg {( dfrac{alpha}{2} )}}}
b – основание равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равностороннего треугольника
Равносторонний треугольник – треугольник, у которого все стороны равны.
Площадь равностороннего треугольника через сторону
{S = dfrac{sqrt{3} cdot a^2}{4}}
a – сторона равностороннего треугольника
Площадь равностороннего треугольника через высоту
{S = dfrac{h^2}{sqrt{3}}}
h – высота равностороннего треугольника
Площадь равностороннего треугольника через радиус описанной окружности
{S = dfrac{3 sqrt{3} cdot R^2}{4}}
R – радиус описанной окружности
Площадь равностороннего треугольника через радиус вписанной окружности
{S = 3 sqrt{3} cdot r^2}
r – радиус описанной окружности
Примеры задач на нахождение площади треугольника
Задача 1
Найдите площадь треугольника со сторонами 13 14 15.
Решение
Для решения задачи воспользуемся формулой Герона.
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}
Для начала нам необходимо найти полупериметр p:
p= dfrac{a+b+c}{2}p= dfrac{13+14+15}{2}= dfrac{42}{2} = 21
Теперь можем подставить его в формулу Герона и найти ответ:
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)} = sqrt{21 cdot (21-13) cdot (21-14) cdot (21-15)} = sqrt{21 cdot (8) cdot (7) cdot (6)} = sqrt{21 cdot 336} = sqrt{7056} = 84 : см^2
Ответ: 84 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.
Решение
Воспользуемся формулой.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 28 cdot sqrt{100^2 – 28^2} = dfrac{1}{2} cdot 28 cdot sqrt{10000 – 784} = dfrac{1}{2} cdot 28 cdot sqrt{9216} = dfrac{1}{2} cdot 28 cdot 96 = 14 cdot 96 = 1344 : см^2
Ответ: 1344 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.
Решение
Задача аналогична предыдущей, поэтому решение очень похоже.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 15 cdot sqrt{17^2 – 15^2} = dfrac{1}{2} cdot 15 cdot sqrt{289 – 225} = dfrac{1}{2} cdot 15 cdot sqrt{64} = dfrac{1}{2} cdot 15 cdot 8 = 15 cdot 4 = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 4
Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)} = dfrac{1}{4} cdot 40^2 cdot sin{(2 cdot 60°)} = dfrac{1}{4} cdot 1600 cdot sin{(120°)} = 400 cdot dfrac{sqrt{3}}{2} = 200 sqrt{3} : см^2 approx 346.41016 : см^2
Ответ: 200 sqrt{3} : см^2 approx 346.41016 : см^2
Проверка .
Задача 5
Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.
Решение
В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{4}{4} sqrt{4 cdot 7^2 – 4^2} = sqrt{4 cdot 49 – 16} = sqrt{196 – 16} = sqrt{180} = sqrt{36 cdot 5} = 6sqrt{5} : см^2 approx 13.41641 : см^2
Ответ: 6sqrt{5} : см^2 approx 13.41641
Проверка .
Задача 6
Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.
Решение
Решим эту задачу по анологии с предыдущей.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{30}{4} sqrt{4 cdot 17^2 – 30^2} = dfrac{30}{4} sqrt{4 cdot 289 – 900} = dfrac{30}{4} sqrt{1156 – 900} = dfrac{30}{4} sqrt{256} = dfrac{30}{4} cdot 16= 30 cdot 4 = 120 : см^2
Ответ: 120 см²
Проверка .
Задача 7
Найдите площадь равностороннего треугольника со стороной 12 см.
Решение
Используем для решения задачи формулу.
S = dfrac{sqrt{3} cdot a^2}{4} = dfrac{sqrt{3} cdot 12^2}{4} = dfrac{sqrt{3} cdot 144}{4} = 36 sqrt{3} : см^2 approx 62.35383 : см^2
Ответ: 36 sqrt{3} : см^2 approx 62.35383 : см^2
Проверка .
Содержание:
- Формула
- Примеры вычисления площади равностороннего треугольника
Формула
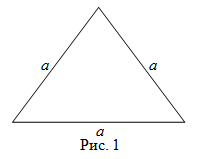
Чтобы найти площадь равностороннего треугольника (рис. 1), нужно квадрат его стороны умножить на
$sqrt{3}$ и поделить на четыре, то есть
$$mathrm{S}_{Delta}=frac{a^{2} sqrt{3}}{4}$$
Эту формулу легко получить из общей
формулы для площади треугольника
$$mathrm{S}_{Delta A B C}=frac{1}{2} a b sin alpha$$
при условии, что $a=b$ (так как треугольник равносторонний) и
$alpha=60^{circ}$ (угол равностороннего треугольника).
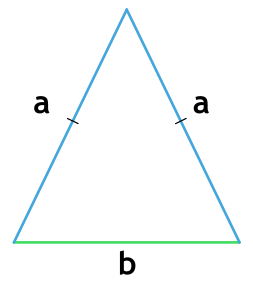
Напомним, что треугольник называется равносторонним, если все его стороны равны.
Примеры вычисления площади равностороннего треугольника
Пример
Задание. Найти площадь равностороннего треугольника
$ABC$, если известно, что его сторона равна 2 дм.
Решение. Подставив заданное значение в формулу, будем иметь:
$mathrm{S}_{Delta A B C}=frac{2^{2} cdot sqrt{3}}{4}=frac{4 cdot sqrt{3}}{4}=sqrt{3}$ (дм2)
Ответ. $mathrm{S}_{Delta A B C}=sqrt{3}$ (дм2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти площадь равностороннего треугольника
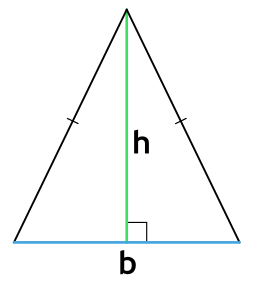
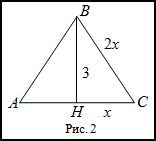
$ABC$, если его высота равна 3 м.
Решение. Сделаем чертеж (рис. 2).
Так треугольник равносторонний, то его высота $BH$ является и
медианой, а это означает, что $AH=HC$ .
Пусть $HC=x$, тогда $AC=2HC=2x=BC$. Рассмотрим прямоугольный треугольник
$BHC$. Записываем для него теорему Пифагора:
$$B C^{2}=B H^{2}+H C^{2}$$
$$(2 x)^{2}=2^{2}+x^{2}$$
Решаем полученное уравнение относительно $x$ :
$4 x^{2}-x^{2}=9 Rightarrow 3 x^{2}=9 Rightarrow x^{2}=3 Rightarrow H C=x=sqrt{3}$ (м)
Отсюда получаем, что
$A C=2 x=2 sqrt{3}$ (м)
А тогда искомая площадь
$mathrm{S}_{Delta A B C}=frac{(2 sqrt{3})^{2} cdot sqrt{3}}{4}=frac{12 sqrt{3}}{4}=3 sqrt{3}$ (м2)
Ответ. $mathrm{S}_{Delta A B C}=3 sqrt{3}$ (м2)
Остались вопросы?
Здесь вы найдете ответы.
Как можно вычислить площадь равсностороннего треугольника?
Согласно формуле, по которой вычисляется площадь S треугольника с равными
сторонами, она равна:
S = √3/4*а, в которой а – это длина стороны фигуры.
Площадь можно также найти следующим образом:
S = a*h/2, где h – это высота.
Высоту можно вычислить, используя теорему Пифагора:
h = а² – (а/2)².
Как можно рассчитать площадь равностороннего треугольника, если известно,
что площадь треугольной фигуры, отсекаемой от него средней линией,
составляет 6 см. кв.?
Обозначим имеющийся треугольник с равными сторонами как АВС. Обозначим
длину стороны как а, и получим, что АВ=ВС=АС=а. Среднюю линию обозначим
как МК. Тогда Sмвк = 6 см. кв.
В случае с равносторонним треугольником:
S = а²√3/4
Зная свойство средней линии треугольника, можно записать следующее
равенство:
МК = АС/2 = а/2.
В этом случае площадь отсекаемого треугольника равна:
Sмвк = (а/2)²*√3/4 = а²√3/16 см.кв.
В условии дано, что Sмвк = 6 см.кв., тогда:
а²√3/16 = 6
а² = 96/√3.
Площадь равностороннего треугольника:
S = а²√3/4 = (96√3)/(4√3) = 96/4 =24 см.кв.
Как можно вычислить площадь равностороннего треугольника при условии, что
его периметр составляет 24 см.?
Найдем сторону равносторонней треугольной фигуры, разделив его периметр на
3:
а = 24:3 = 8 см.
Тогда площадь этой фигуры равна:
S =1/2a²sin 60° = 1/2*64*√3/2 = 16√3 см.кв.
Что представляет собой формула площади равностороннего треугольника?
Обозначив одну из сторон равносторонней треугольной фигуры как а, а
высоту, проведенную к ней, – как h, то формула расчета площади этой фигуры
будет выглядеть так:
S=ah/2.
Принимая во внимание то, что все стороны данной треугольной фигуры равны,
то его высоту можно выразить через сторону и вычислить, используя теорему
Пифагора:
h² = а²-(а/2)² = h² = а²- а²/4 = 3а²/4
h = (а√3)/2
Тогда площадь данной фигуры равна:
S = ½ a* h = ½ a*(а√3)/2 = (a²√3)/4
Как выразить длину стороны а из формулы площади равностороннего
треугольника?
Для расчета площади треугольника, длины всех сторон которого равны,
используется формула:
S=a²√3/4
Перенесем 4 в правую часть равенства:
4S=a²√3.
Тогда:
a² = 4S/√3
а = √4S/√3.
Какая формула используется для вычисления площади равностороннего
треугольника с длиной стороны а?
Если известно, что сторона равносторонней треугольной фигуры равна а, то
его площадь рассчитывается так:
S = а²√3/4.
Каким образом можно привести доказательство теоремы о площади
равностороннего треугольника?
Треугольник имеет два катета – АВ и ВС. Его гипотенуза – ВС. Так как
фигура является равносторонней, то АВ = АС.
Требуется доказать, что площадь треугольной фигуры, стороны которой
одинаковы, равна произведению длин его катетов, разделенному на два.
Превратим имеющийся треугольник в квадрат, проведя перпендикуляр из его
углов, и получим что:
ΔВАС = ΔВСD.
Площадь квадрата равна:
S = а*b.
Диагональ квадрата ВС является гипотенузой треугольника, которая делит
квадрат на 2 равные части. Из этого следует, что площадь треугольника
равна половине площади квадрата. Что и требовалось доказать.
Как вычислить площадь равностороннего треугольника со стороной длиной 9 см.?
Имеется треугольник АВС с равным сторонами.
ВН = 9 см.
Площадь данной фигуры находится по формуле:
S=1/2*АС*ВН,
в которой АС – основание треугольной фигуре, по длине равное любой из
сторон (равносторонний Δ), ВН – высота.
Предположим, что АС = 2а см. Тогда:
АН = АС/2 = ½*2а = а см.
Согласно теореме Пифагора:
АВ² = ВН²+АН².
В данном случае:
(2а)² = 9²+а²
Переносим а² в правую часть уравнения:
4а²-а² = 81
Упрощаем:
3а² = 81.
Отсюда:
а² = 81/3 = 27
а=√27=√9×3=3√3 см.
Теперь можно найти площадь:
S=1/2*9*3√3=1/2*27/√3=27√3/2=13,5√3 см.кв.
Какому числу равна площадь равностороннего треугольника с основанием длиной
6 см.?
Известна формула расчета площади треугольника:
S=1/2*h*b.
Проведем высоту h, которая в равностороннем треугольнике представляет
собой также биссектрису и медиану.
Воспользуемся теоремой Пифагора для вычисления высоты:
h = √(36-9) = √27 см.
Тогда:
S = h*3 = 3√27 см.кв.
Возможно ли привести доказательство того, что площадь равностороннего
треугольника равна √3*a²/4, в которой длина его стороны обозначена как а?
Доказать, что приведенное в задании утверждение является верным, можно,
если превратить имеющуюся треугольную фигуру в параллелограмм/, площадь
которого равна произведению длины стороны и высоты.
Параллелограмм состоит из двух треугольников, которые равны. Это значит,
что площадь одной из треугольных фигур находится так:
S = a*h /2.
Высоту можно выразить через определение синуса.
Все углы в равносторонней треугольной фигуре равны и составляют 60
градусов (180/3).
sin(60) = V3/2.
Из определения синуса следует:
h/a = sin(60).
Это значит, что:
h = a*V3/2.
Значит:
S = a*a*V3/4.
Почему площадь равностороннего треугольника равна a^2√3/4?
Известно, что площадь любого треугольника можно найти по формуле:
S = 1/2*a*b*sinA,
в которой стороны треугольника обозначены как а и b, а угол, образованный
ими, – как А.
Доказано, что каждый угол равносторонней треугольной фигуры составляют 60
градусов (sin60 =sqrt(3)/2), а его стороны имеют одинаковые длины. Если
подставить эти значения в формулу, то получим:
S = a22√3/4.
Как найти площадь равностороннего треугольника при условии, что длина каждой
его стороны составляет 12 см.?
Площадь треугольника с равными сторонами вычисляется по формуле:
S = √3/4*a².
В данном случае:
S= √3/4*12²= √3*144 /4*1 = 36√3 ≈ 62,35 см.кв.
Согласно формуле Герона:
S = √(р(р-а)(р-a)(p-a))
Для данного треугольника:
Р = 12*3 = 36 см.
Р = р/2 = 36/2 = 18 см.
Тогда:
S = √ (18× (18-12)³) = √(18*6³) = √(18×216)=√3888 ≈ 62,35 см. кв.
Как вычислить площадь правильного равностороннего треугольника, зная радиус
круга R?
Площадь треугольника с одинаковыми сторонами считается как:
S = a²√3/4.
Радиус r окружности, которая вписана в данный Δ, равен a√3/6. Значит:
а = 2√3r.
Считаем площадь треугольника:
S = 4*3r²√3/4 = 3√3r².
Радиус R окружности, которая описана около правильной треугольной фигуры,
равен a/√3. Следовательно, а = R√3.
В этом случае:
S = R²*3√3/4 = 3√3R²/4.
Известно, что площадь правильного треугольника равна 100√3 м.кв. Как
вычислить его сторону?
Площадь треугольника равна:
(a²√3)/4.
В данном случае:
100√3=(a²√3)/4
Тогда:
a²√3=400√3.
Находим а:
a²√3 = 400√3
a² = 400
a = 20 см.
Чему равна площадь правильного треугольника при условии, что диаметр
окружности, вписанной в него, = 10 см.?
Если d = 10 см., то r = 10/2 = 5 см.
Известно, что:
r = а√3/6, где а – это длина стороны правильного Δ.
Значит:
5 = а√3/6.
Отсюда:
а = 30/√3 = 10√3 см.
Тогда:
SΔ = a²√3/4 =(10√3)³ *√3/4 = 75√3 см. кв.
Чему равна площадь правильного треугольника со стороной 4 дм.?
Известно, что:
S = 1/2 * a * a sin 60 = 1/2 * 4 * 4 * √3/2 = 4√3 дм.кв.
Площадь также можно найти так:
S = a²√3/4 = 16√3/4 = 4√3 дм.кв.
Как найти площадь правильного треугольника, зная, что длина описанной около
него окружности равна 4Пи см.?
Длина окружности через радиус находится так:
L=2πR.
Значит:
R=L/2π=4π/2π=2 у.е.
Имеем правильный треугольник, значит длина его стороны:
a=R*√3=2√3 у.е.
Можем найти SΔ:
S = √3/4a² = √3/43*3 = 3√3 у.е.кв.
Чему равна площадь правильного треугольника и его стороны, если его высота =
14 см.?
В правильном треугольнике длины всех сторон одинаковы. Это значит, что
каждую из них можно обозначить как х. Тогда:
Р (периметр) = х + х + х = 3х см.
Площадь будет равна:
S = 1/2 h * x = 14/2*x = 7х см.кв.
Как найти площадь правильного треугольника с равными сторонами при условии,
что радиус круга R?
Площадь треугольной фигуры с равными сторонами считается как:
S = a²√3/4.
Радиус окружности, вписанной в этот Δ, составляет a√3/6. Тогда а = 2√3r.
Находим площадь треугольника:
S = 4*3r²√3/4 = 3√3r².
Радиус R окружности, которая описана около правильного Δ, составляет a/√3.
Это означает, что а = R√3.
Теперь можем высчитать площадь треугольника:
S = R²*3√3/4 = 3√3R²/4.
Как найти площадь правильного треугольника при условии, что расстояние от
его центра до вершины составляет 2 м.?
Центр правильно треугольной фигуры также является центральной точкой
описанной около нее окружности. Ее радиус представляет собой расстояние от
центра до вершины фигуры:
а=R√3=2√3
Все углы в правильном треугольнике являются одинаковыми и равны по 60
градусов (180/3).
Площадь треугольной фигуры рассчитывается как:
а²sin60°/2=(2√3)²√3/2/2=6√3 м.кв.
Как найти площадь правильного треугольника, если определено, что сторона
имеет длину, аналогичную длине стороны ромба с диагоналями 10 см. и 12 см.?
Предположим, что BD = 10 см., а АС = 12 см.
Диагонали ромба перпендикулярны и делятся на две равные части, пересекаясь
в определенной точке.
ΔАВО: ∠АОВ = 90°, АО = АС/2 = 6, ВО = BD/2 = 5.
Согласно теореме Пифагора:
АВ = √(АО² + ВО²) = √(36 + 25) = √41.
Треугольник имеет равные стороны, длина каждой из которых аналогична длине
стороны ромба:
а = √41.
Тогда:
SΔ = a²√3/4 = 41√3/4 см.кв.
Как найти площадь правильного треугольника периметром 6 см.?
Если длина стороны правильного треугольника указана, то его площадь
вычисляется следующим образом:
S = a²√3/4.
Согласно определению правильного треугольника, длины всех его сторон
одинаковые. Исходя из этого можно найти его сторону, разделив периметр на
три:
а = 6/3 = 2 см.
Ищем площадь, подставив в равенство значение а:
S = 2²√3/4 = S 4√3/4 = √3 см.кв.
Как найти площадь правильного треугольника при условии, что окружность,
которая вписана в него, имеет радиус длиной 4 см.?
Площадь треугольника, имеющего стороны одинаковой длины, может быть
рассчитана через длину его стороны без применения формулы радиуса
окружности, которая вписана в него. Для данной фигуры верно утверждение о
том, что высота, биссектриса и медиана делятся в точке пересечения в
отношении 2:1. При схематичном изображении можно увидеть, что треугольная
фигура АВС включает 6 треугольников с прямыми углами, которые имеют
одинаковый катет (R) и гипотенузу (АО=ВО=СО). Следовательно, площадь
треугольника АВС будет представлять собой сумму площадей всех 6
треугольников, формирующих его.
Какова формула вычисления площади равностороннего треугольника со стороной
а?
Если сказано, что сторона равносторонней треугольной фигуры равна а, то
его площадь можно найти:
S = a²√3/4.
Как определить, чему равна длина стороны треугольника с равными сторонами,
зная формулу, по которой вычисляется площадь равностороннего треугольника
(S=√3/4 а²) и то, что она равна 9√3см²?
Если S=√3/4 а², то в данном случае S=9√3, что означает: 9√3=√3/4 а².
Выразим а²:
а² = 9√3:√3/4 = 9√3 x 4√3 = 36
а = +-√36 = +- 6.
Так как длина стороны не может быть отрицательным числом, то a = 6 см.
Какой вид имеет формула, которая отражает зависимость площади
равностороннего треугольника от длины его сторон?
Доказано, что равносторонний треугольник имеет равные углы по 60 градусов.
Также известна формула вычисления площади данной фигуры путем умножения
длин двух его сторон и синуса угла, который они образуют:
S = 1/2*a*a*sin 60 = a²√3/4 см.кв.
Чему равна площадь равностороннего треугольника и длина его медианы, если
известно, что его сторона составляет а?
Если указано, что длина стороны равностороннего треугольника составляет а,
то его площадь равна:
S=a²√3/4.
Медиана, проведенная в треугольнике с равными сторонами, также
представляет собой его биссектрису и высоту. Из этого следует, что:
h=a√3/2.
Ответ: Площадь треугольника = a²√3/4 см.кв., его медиана = a√3/2 см.
Как определить площадь равностороннего треугольника со стороной, длина
которой составляет 8√2 см?
В случае с треугольником с равными сторонами, высота представляет собой
также медиану, делящую на две равные части сторону, на которую она
опущена. Если применить в данном случае теорему Пифагора, то высота равна:
h = √((8√2)²-(4√2)²)=4√6 см.
Теперь есть возможность найти площадь:
S = (1/2)*8√2*4√6 = 32√3 см. кв.
Площадь также можно найти по формуле для треугольника с равными сторонами:
S =(√3/4)*a² или S =(√3/4)*128 = 32√3 см. кв.
Дано два равносторонних треугольника, площадь одного из которых превышает
площадь другого в три раза. Чему будет равна сторона второго равностороннего
треугольника, при условии, что сторона первого из них составляет 1 см.?
Для расчета площади треугольника с равными сторонами есть формула:
S = a²√3/4.
Найдем площадь меньшего из треугольников, подставив значение а:
S₁ = 12 √3/4 = √3/4 см.кв.
Известно, что площадь второго треугольника больше площади первой фигуры в
три раза. Тогда:
S₂ = 3√3/4.
Очевидно, что сторона большего треугольника составляет √3 см.
Сторона равностороннего треугольника равна 14 см. Чему будет равна его
площадь, умноженная на √3?
Формула площади для треугольника с равными сторонами:
S = а²*√3/4.
Подставляем значение а:
S = 14²*√3/4 = 49√3 см. кв.
Умножаем полученное число на √3:
49√3*√3 = 49*3 = 147 см.
Читать дальше: как найти площадь круга.
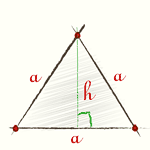
Площадь равностороннего треугольника, формула
Площадь равностороннего треугольника вычисляется по классической формуле площади треугольника — произведение половины основания треугольника на его высоту. Высоту мы подставим в эту формулу из формулы высоты равностороннего треугольника
[S=frac{1}{2}ah]
[S=frac{sqrt{3}}{4}a^2]
(a – сторона равностороннего треугольника)
Вычислить, найти площадь равностороннего треугольника по формуле (2)
Ссылки по теме
Площадь равностороннего треугольника |
стр. 306 |
|---|