Светило науки – 24 ответа – 0 раз оказано помощи
Сечение шара(сферы) плоскостью – всегда является кругом. Центр этого круга – это основание
перпендикуляра(CH), опущенного из центра(C) шара на секущую плоскость. Площадь
круга равна pi*R^2.
Так как плоскость пересекает шар через конец радиуса, то получаем прямоугольный
треугольник ABC. BC – радиус сферы(собсна, через конец которого и проходит
секущая плоскость), но и KC – тоже радиус сферы(который перпендикулярен радиусу
ВС), а отрезок AC – это часть радиуса КС, которую отсекла секущая
плоскость, CH – высота, опущенная на
гипотенузу АВ. Теперь все сводится к тому, чтобы найти радиус BH
круга(сечения). По условию нам дано, что радиус сферы равен 12, и угол, под
которым плоскость сечет шар – 30°. Рассмотрим прямоугольный треугольник ВНС. ВС – гипотенуза треугольника ВНС, угол НВС
равен 30°. Вспомним, что катет
прямоугольного треугольника, лежащий напротив угла 30° равен половине гипотенузы, следует, что катет НС равен
половине ВС => HC=6. По теореме Пифагора ищем ВН. ВН^2=BC^2-HC^2.
BH^2=144-36. BH=√108.
Все,
теперь ищем площадь сечения(круга). S=pi*R^2 S=pi*(√108)^2
S=108pi.
Ответ:
108pi
(К
слову, пользовался программами Cinema 4D и Photoshop, чтобы показать сечение и треугольник) )0))


Анастасия Я
Ученик
(121),
на голосовании
10 лет назад
Радиус шара 4, Через конец радиуса проведена плоскость под углом 60* к нему. Найти площадь сечения.
Голосование за лучший ответ
псевдоним
Ученик
(176)
10 лет назад
ОАВ-равнобедренный. нужно найти АВ, чтобы подставить в формулу S сеч = Pi * r (в квадрате) .
АВ= 2 * ОА * cos ОАВ, подставляем АВ= 2 * 4 * 0.5 = 4.
АВ=4. АВ-диаметр, АВ/2= радиус. r сечения = АВ/2= 4/2 = 2.
Подставляем в формулу площади сечения S=Pi * r (в квадрате) = Pi * 2 в квадрате = 4 Pi/
Ответ: S сечения = 4 Pi.
gatideith483
Вопрос по геометрии:
Диаметр шара равен 4m.Через конец диаметра проведена плоскость под углом 30 градусов к нему.Найдите площадь сечения шара этой плоскостью. 11 КЛАСС РЕШИТЬ ПОДРОБНО И НАРИСОВАТЬ РИСУНОК
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
lamendrfuim310
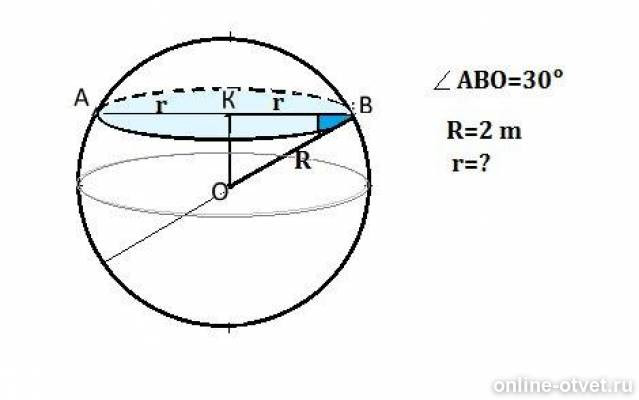
Сделаем рисунок.
Соединим центр шара с центром сечения ( Это круг. Любое сечение шара является кругом).
По условию диаметр шара и диаметр сечения составляют угол 30°.
Радиус R шара – половина диаметра и равен 2 m
Площадь сечения – это площадь круга с радиусом r = КВ.
Радиус сечения найдем по т.Пифагора из прямоугольного треугольника ОКВ.
ОК противолежит углу 30°, поэтому равен половине ОВ=1m.
KB=√(ОВ²-КВ²)=√(4-1)=√3m
S сечения=πr²= π(√3m)² =3π m²
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Задача 23827 Диаметр шара равен d. Через конец…
Условие
Диаметр шара равен d. Через конец диаметра проведена плоскость под углом 45° к нему. Найдите площадь сечения шара этой плоскостью.
предмет не задан
87759
Решение
★
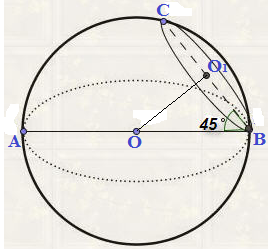
АВ=d;
OA=ОВ=ОС=R
R=d/2
Cечение шара плоскостью – круг,
CB– диаметр этого сечения.
Плоскость проведена под углом 45^(o) к диаметру шара, значит CВ составляет угол 45^(o) c диаметром шара AB.
Треугольник СОВ – равнобедренный
ОО1- высота, медиана и биссектриса.
Из прямоугольного треугольника
ОО1В:
ОО1=ОВ* sin 45^(o)=dsqrt(2)/4
r(cсечения)=О1В=ОО1=dsqrt(2)/4
S(ceчения)=Pir^2=Pi*(dsqrt(2)/4)^2=Pid^2/8
Написать комментарий
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности сегмента шара, а также разберем пример решения задачи для демонстрации их практического применения.
- Определение сегмента шара
-
Формулы для нахождения площади сегмента шара
- Площадь основания
- Площадь сферической поверхности
- Площадь полной поверхности
-
Пример задачи
Определение сегмента шара
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.
- R – радиус шара;
- r – радиус основания сегмента;
- h – высота сегмента; это длина перпендикуляра от центра его основания (точка O2) до точки на поверхности шара.
Связь между радиусом основания сегмента, его высотой и радиусом шара:
Формулы для нахождения площади сегмента шара
Площадь основания
Основанием шарового сегмента является круг, площадь (S) которого находится по стандартной формуле (в расчетах число π округляется до 3,14):
Sосн. = πr 2
Примечание: если известен диаметр круга (d), чтобы найти радиус (r), нужно первое разделить на второе, то есть: r = d/2.
Площадь сферической поверхности
Чтобы найти площадь (S) сферической/внешней поверхности шарового сегмента, необходимо знать его высоту и радиус самого шара.
Sсфер. пов. = 2πRh
Площадь полной поверхности
Чтобы найти площадь (S) полной поверхности сегмента шара, необходимо сложить площади его основания и внешней поверхности.
Sполн. = Sосн. + Sсфер. пов. = π (2Rh + r 2)
Пример задачи
Дан шар радиусом 6 см. Найдите полную площадь шарового сегмента, если известно, что его высота равняется 2,4 см, а радиус основания – 4,7 см.
Решение
Воспользуемся формулами, приведенными выше, подставив в них известные по условиям задачи значения.
Sосн. = 3,14 ⋅ (4,7 см) 2 = 69,3626 см 2
Sсфер. пов. = 2 ⋅ 3,14 ⋅ 6 см⋅ 2,4 см = 90,432 см 2
Sполн. = Sосн. + Sсфер. пов. = 69,3626 см 2 + 90,432 см 2 = 159,7946 см 2


