Как рассчитать площадь правильного шестиугольника
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник – многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
a:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через сторону:
a – сторона шестиугольника.
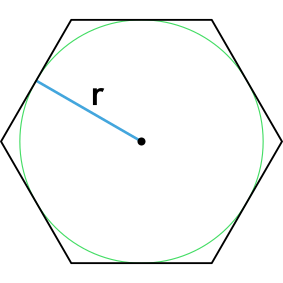
Через радиус описанной окружности
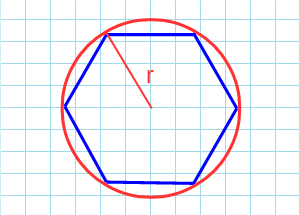
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
r – радиус описанной окружности.
Через радиус вписанной окружности
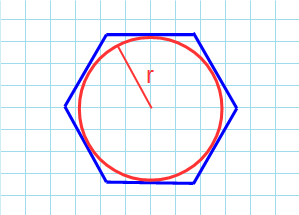
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности:
r – радиус вписанной окружности.
Калькулятор
На этой странице вы найдете калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного шестиугольника по стороне или радиусам вписанной и описанной окружностей.
Шестиугольник представляет собой многоугольник, к которого все внутренние углы равны 120 градусов, а все стороны равны между собой.
Содержание:
- калькулятор площади правильного шестиугольника
- формула площади правильного шестиугольника через длину стороны
- формула площади правильного шестиугольника через радиус вписанной окружности
- формула площади правильного шестиугольника через радиус описанной окружности
- формула площади правильного шестиугольника через периметр
- примеры задач
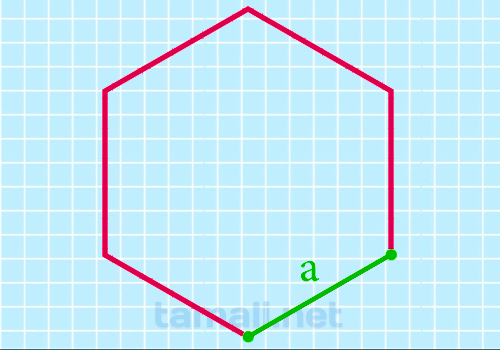
Формула площади правильного шестиугольника через длину стороны
S = dfrac{3 sqrt{3} a^2}{2}
a – длина стороны шестиугольника
Формула площади правильного шестиугольника через радиус вписанной окружности
S = 2 sqrt{3}r^2
r – радиус вписанной окружности
Формула площади правильного шестиугольника через радиус описанной окружности

S = dfrac{3 sqrt{3} R^2}{2}
R – радиус описанной окружности
Формула площади правильного шестиугольника через периметр

S = dfrac{P^2 sqrt{3}}{24}
P – периметр шестиугольника
Примеры задач на нахождение площади правильного шестиугольника
Задача 1
Найдите площадь правильного шестиугольника, радиус вписанной окружности которого равен 9 см.
Решение
Исходя из того, что из условия задачи нам известен радиус вписанной окружности, мы воспользуемся формулой.
S = 2 sqrt{3}r^2 = 2 sqrt{3} cdot 9^2 = 2 sqrt{3} cdot 81 = 162 sqrt{3} : см^2 approx 280.59223 : см^2
Ответ: 162 sqrt{3} : см^2 approx 280.59223 : см^2
Проверить правильность решения нам поможет калькулятор .
Задача 2
Найдите площадь правильного шестиугольника со стороной равной 1 см.
Решение
Для этой задачи нам подойдет формула.
S = dfrac{3 sqrt{3} a^2}{2} = dfrac{3 sqrt{3} cdot 1^2}{2} = dfrac{3 sqrt{3} cdot 1}{2} = dfrac{3 sqrt{3}}{2} : см^2 approx 2.59808 : см^2
Ответ: dfrac{3 sqrt{3}}{2} : см^2 approx 2.59808 : см^2
Проверим ответ .
В публикации представлены онлайн-калькуляторы и формулы, позволяющие вычислить площадь правильного шестиугольника через длину его стороны или радиус описанной окружности.
Содержание
скрыть
-
Расчет площади
- Через сторону
- Через радиус описанной окружности
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
Через сторону
Формула расчета

Через радиус описанной окружности
Формула расчета

Правильный шестиугольник, многоугольнике с 6 вершинами, вычислить его параметры. Шестиугольник-это фигура, из которой можно складывать мозаику (черепицу). Введите одно из известных значений. Затем нажмите кнопку вычислить.
.
Поделиться расчетом:
Калькулятор шестиугольников
Длина стороны(a)
Большая диагональ(d1)
Меньшая диагональ(d2)
Периметр(p)
Площадь(S)
Радиус вписанной окружности(r)
Вычислить
Очистить
Формулы:
 d = 2 * a
d = 2 * a
d2 = √3 * a
p = 6 * a
S = 3/2 * √3 * a2
r = √3 / 2 * a
Высота = d2 = 2 * r
Радиус окружности = a
Внутренние углы: 120°, 9 диагоналей





Шестиугольник — многоугольник, у которого есть шесть сторон и шесть углов. В правильном заданном
многоугольном геометрическом объекте все стороны равняются друг другу, а углы формируют шесть
равносторонних треугольников.
Площадь правильной фигуры с шестью углами — положительная величина некоторой области плоскости,
занимаемой данным многоугольным геометрическим объектом.
Выделяют ряд методов нахождения площади этого многоугольника, зависимо от его типа.
- Площадь правильного шестиугольника через длину стороны
- Площадь правильного шестиугольника через радиус описаной окружности
- Площадь правильного шестиугольника через радиус вписаной окружности
- Площадь правильного шестиугольника через длинную диагональ
- Площадь правильного шестиугольника через короткую диагональ
- Площадь правильного шестиугольника через периметр
Через длину стороны
По той причине, что выпуклый шестиугольник включает в себя шесть равносторонних треугольников, тогда
формула нахождения требуемой величины через длину стороны выглядит следующим образом:
S = (3√3*a²)/2
где a — это продолжительность стороны.
Цифр после запятой:
Результат в:
Рассмотрим пример. Пусть длина стороны эквивалентна 8. Тогда, согласно этой формуле, заданную
характеристику замкнутого выпуклого шестиугольника будет примерно равна 166.
Всё достаточно
просто, если сторона заранее известна. Если же эта величина нам не дана, но известен периметр или
апофема — высота одного из шести равносторонних треугольников — тогда длину стороны можно
высчитать.
В случае, если известен периметр, его необходимо поделить на шесть, таким образом получается длина
стороны. К примеру, если периметр равен 36, то, поделив 36 на 6, получается 6 — это и есть
протяжённость стороны.
Если известна лишь апофема, тогда можно посчитать длину стороны, подставив апофему в формулу b = x√3 и умножив ответ на 2. Всё это потому, что апофема — это сторона
x√3 составляемого ей треугольника с углами 30, 60 и 90 градусов. К примеру, если апофема 11√3, то
x = 11, а протяжённость стороны будет эквивалентна 22.
Через периметр
Если при изучении правильной фигуры с шестью углами нам известен только его периметр, несложно
рассчитать площадь этой фигуры по такой формуле:
Цифр после запятой:
Результат в:
S = (3√3*(p/6)²)/2
где p — это периметр фигуры.
Допустим, если периметр будет равняться 24, тогда площадь будет примерно эквивалентна 42. Если в
качестве периметра возьмём число 50, тогда площадь фигуры окажется 180.
Через длинную диагональ
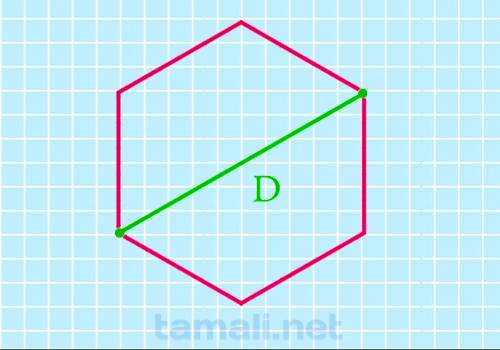
Длинная или большая диагональ шестиугольника — это диаметр описанной вокруг него плоской кривой, как
правило, она равняется двум его сторонам.
Цифр после запятой:
Результат в:
Используем такое выражение для подсчёта площади подобного правильного многоугольного геометрического
объекта через длинную диагональ этого множества точек:
S = (3√3*D²)/8
где D — это длинный отрезок, соединяющий несмежные вершины.
К примеру, если D = 6, тогда заданная характеристика замкнутого выпуклого
многоугольника будет приблизительно равна 23. Если в качестве длинной диагонали возьмём 8, тогда
величина будет примерно эквивалентна 42.
Через короткую диагональ
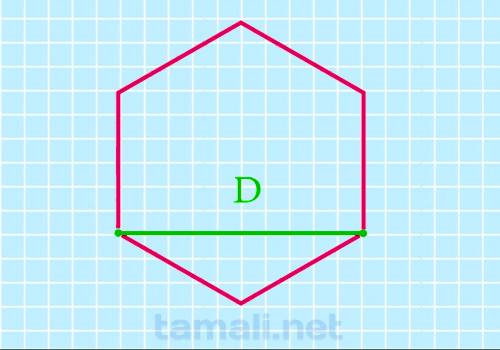
Меньшая или короткая диагональ правильного шестиугольника в √3 раз длиннее его стороны, также она
образует с ней прямой угол.
Цифр после запятой:
Результат в:
Если известна короткая диагональ такого выпуклого многоугольника, то с её помощью можно найти площадь
этой фигуры следующим образом:
S = (√3*D²)/2
где D — это протяжённость короткого отрезка, соединяющего несмежные
вершины.
К примеру, если длина такой диагонали будет равна 14, тогда необходимая характеристика фигуры будет
примерно равняться 170. Если же в качестве D мы возьмём 2, тогда величина
окажется всего лишь 3.
Через радиус описанной окружности
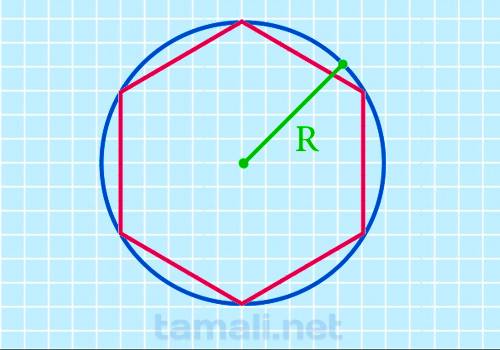
Шестиугольник считается правильным многоугольником, ведь все его стороны и углы эквивалентны друг
другу. Соответственно, около такого многоугольника можно описать окружность.
Чтобы найти площадь выпуклого многоугольника через радиус описанной окружности, необходимо
воспользоваться такой формулой:
S = (3√3*R²)/2
где R — это отрезок, соединяющий центр и любую точку описанной замкнутой
плоской кривой.
Цифр после запятой:
Результат в:
К примеру, если отрезок, соединяющий центр и любую точку, равняется 5, тогда заданная характеристика
замкнутой фигуры будет примерно равна 65. Если же в качестве радиуса возьмём число 12,
соответственно, заданная характеристика замкнутой фигуры получится примерно 374.
Через радиус вписанной окружности
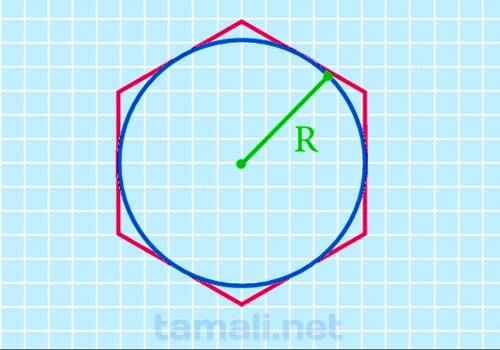
Шестиугольник считается правильным многоугольником, ведь все его стороны и углы равны друг другу.
Соответственно, во всякий шестиугольник можно вписать окружность.
Формула для расчёта площади следующего выпуклой фигуры с шестью углами через радиус вписанной
окружности будет выглядеть следующим образом:
S = √3*r²
где r — это отрезок, соединяющий центр и любую точку вписанной замкнутой
плоской кривой.
Цифр после запятой:
Результат в:
К примеру, если этот отрезок, соединяющий центр и любую точку, равен 14, тогда необходимая величина
этого множества точек будет примерно равна 679. Если в качестве отрезка, соединяющего центр и любую
точку, возьмем 4, тогда площадь будет приблизительно равна 55.
Что такое правильный шестиугольник
Этот многоугольный геометрический объект имеет определённые свойства:
- Каждый угол этой фигуры равняется 120 градусам;
- Вокруг правильного шестиугольника можно описать окружность, причем единственную, а её радиус
равняется его стороне; - Большие диагонали такого выпуклого многоугольника разделяют его на шесть равносторонних
треугольников, высота каждого равняется радиусу вписанной в выпуклый многоугольник окружности; - Центры вписанной и описанной окружностей около подобного выпуклого многоугольника — это точка
пересечения больших диагоналей этого множества точек.
Эта фигура очень часто встречается в природе, технике и культуре. К примеру:
- Пчелиные соты изображают разделение плоскости на выпуклые шестиугольники;
- Некоторые сложные молекулы углерода имеют гексагональную кристаллическую решётку;
- Сечение гайки и большинства карандашей описывается таким выпуклым многоугольником;
- Гексаграмма — это шестиконечная звезда, сформированная двумя правильными треугольниками. Также
её называют звездой Давида, она считается символом иудаизма.
