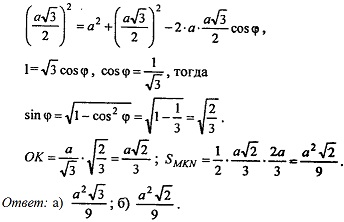я могу помочь с этим заданием
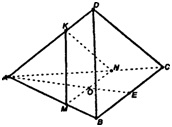
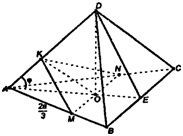
а) Пусть т. О – центр грани АВС. Построим МК || DB, MN || ВС. пл .MKN – искомое сечение.
Пусть ребро тетраэдра равно а. Тогда
Т.к. ΔADB – равносторонний, а КМ || DB, то ΔАМК – также равносторонний, АМ=КМ=
(углы с соответственно параллельными и одинаково направленными сторонами):
б) Построим отрезок в пл. ADO. Т.к. пл.
то
Т.к. и
то
Значит, ΔKMN — искомое сечение,
ΔAMN – равносторонний, MN = AM =
Из ΔADE по теореме косинусов имеем:
DE2 = AD2 + АЕ2 – 2 ∙ AD ∙ АЕ ∙ cos φ,
2023-03-27
Дан правильный тетраэдр с ребром $a$. Найдите площадь сечения плоскостью, проходящей через центры трёх его граней.
Решение:
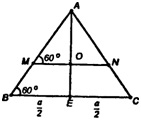
Пусть $M$, $K$ и $N$ – центры граней соответственно $ABC$, $BCD$ и $ABD$ правильного тетраэдра $ABCD$, а $P$ и $Q$ – середины рёбер соответственно $AB$ и $BC$.
Поскольку $DN:NP=DK:KQ=2:1$, прямая $NK$ параллельна $PQ$. Значит, прямая $NK$ параллельна плоскости $ABC$. Секущая плоскость проходит через прямую $NK$, параллельную плоскости $ABC$ и имеет с плоскостью $ABC$ общую точку $M$, следовательно, эти плоскости пересекаются по прямой $l$, параллельной $NK$, а значит, и $PQ$ (см. задачу @H8003). Пусть прямая $l$ пересекает рёбра $AB$ и $BC$ в точках $E$ и $F$ соответственно, а $T$ – середина $AC$. Тогда
$BE:AB=BF:BC=BM:BT=2:3.$
Аналогично получим, что секущая плоскость пересекает ребро $BD$ в точке $L$, для которой $BL:BD=2:3$. Значит, сечение тетраэдра плоскостью $MKN$ – треугольник $ELF$, подобный треугольнику $ADC$ с коэффициентом $frac{2}{3}$. Следовательно,
$S_{Delta ELF}=left(frac{2}{3}right)^{2}S_{Delta ADC}=frac{4}{9}cdotfrac{a^{2}sqrt{3}}{4}=frac{a^{2}sqrt{3}}{9}.$
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найдите площадь сечения правильного тетраэдра PABC плоскостью, параллельной рёбрам PA и PC и проходящей через середину ребра PB, если все рёбра тетраэдра равны 8.
2
Найдите площадь сечения правильного тетраэдра PABC плоскостью, параллельной рёбрам PA и PC и проходящей через середину ребра PB, если все рёбра тетраэдра равны 4.
Аналоги к заданию № 488: 489 Все
3
Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через середины рёбер BC и PC параллельно ребру AC, если все рёбра тетраэдра равны 10.
4
Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через середины рёбер BC и PC параллельно ребру AC, если все рёбра тетраэдра равны 6.
Аналоги к заданию № 490: 491 Все
5
Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через точки, делящие рёбра PC и BC в отношении считая от вершины C, параллельно ребру BP, если все рёбра тетраэдра равны 3.
Пройти тестирование по этим заданиям
nghacun200
Вопрос по геометрии:
Ребро правильного тетраэдра равно a. Найдите площадь сечения тетраэдра, проходящего через одно из ребер и делящего пополам двугранный угол при этом ребре.
С рисунком и доказательством пожалуйста)
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
kedoveanghun411
Решение в скане. Арифметику бы проверить…
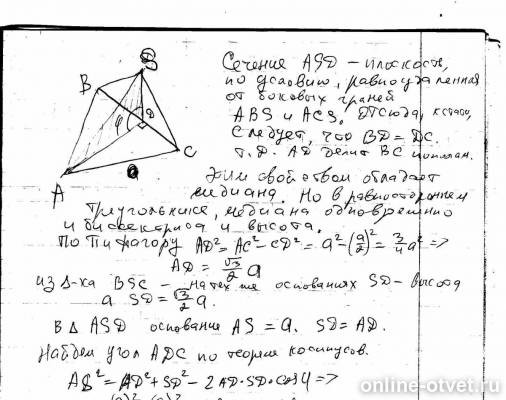

Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Ребро правильного тетраэдра DABC равно а.
Постройте сечение тетраэдра, проходящее через середины ребер DA и AB параллельно ребру BC, и найдите площадь этого сечения.
––––––––––––––––––––––––
Тетраэдр называется правильным, если все его грани — равносторонние треугольники.
Сечение пройдет через середины ребер АD и АВ по линии D1B1– это средняя линия ∆ АВD.
Сечение, параллельное ВС – проходит через В1С1 – среднюю линию ∆ АВС.
Каждая сторона построенного сечения – средняя линия треугольника. ограничивающего грань тетраэдра, и по свойству средней линии равна а/2,
т.е. проведенное через середины ребер сечение – правильный треугольник со сторонами, равными а/2
Его площадь найдем по формуле площади равностороннего треугольника:
S=(a²√3):4
S=(a/2)²√3):4=(a²√3):16
_______________
Вариант решения:
Треугольник. получившийся в сечении, подобен треугольнику ВСD с коэффициентом подобия
k=( а/2):а=1/2
Отношение площадей подобных фигур равно квадрату коэффициента их подобия.
S1:S=k²=1/4
S ∆ CDB=(a²√3):4
S сечения в 4 раза меньше и равно (a²√3):16