Как найти площадь сечения трапеции в кубе - Сайт, где вы сможете решить свои вопросы

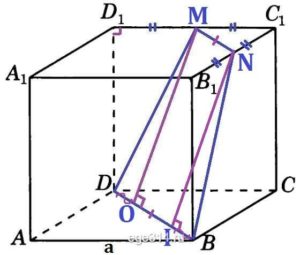
Поскольку через 3 точки можно провести только одну плоскость. ЕК параллельна В1С (грани, на которых они лежат, параллельны)
В этой трапеции большее основание равно диагонали грани куба.
Меньшее основание равно гипотенузе треугольника АКЕ, где АК=АЕ=1/2а
Боковые стороны этой равнобедренной трапеции равны гипотенузе треугольника КСD, где КD=1/2а, DС=а.

Для нахождения высоты равнобедренной трапеции можно использовать это свойство:
Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой – полуразности оснований. И уже из получившегося маленького треугольника, где катеты высота и полуразность оснований, а гипотенуза – сторона трапеции, найти высоту трапеции по её теореме Пифагора.

Есть формула, где для нахождения площади трапеции можно обойтись без высоты.
Формула, где a, b — основания, c и d — боковые стороны трапеции:

Источник

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

Скачиваний:

Добавлен:

15.05.2015

Размер:

406.75 Кб

Скачать

ПРИМЕНЕНИЕ ТЕОРЕМЫ О ПЛОЩАДИ ОРТОГОНАЛЬНОЙ ПРОЕКЦИИ МНОГОУГОЛЬНИКА ПРИ РЕШЕНИИ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ

Бардушкин В.В., Белов А.И., Ланцева И.А., Прокофьев А.А., Фадеичева Т.П.

Существует несколько методов решения стереометрических задач на вычисление площадей сечений, поверхностей многогранников и углов (между плоскостями, между прямой и плоскостью и т.д.). Эти методы достаточно подробно рассмотрены в школьных учебниках, изложены в различных пособиях по стереометрии. Так, например, при вычислении площадей широко применяется подход, основанный на разбиении многоугольника на части (на треугольники и четырёхугольники). Если в каждой из частей удаётся вычислить длины сторон (или диагоналей четырёхугольника) и какие-нибудь углы, то можно по известным формулам найти их площади, а значит, решить задачу. Довольно большое значение придаётся векторно-координатному методу решения подобных задач. Однако, на наш взгляд, многие из авторов-составителей не уделяют должного внимания методу вычисления площадей и углов, связанному с ортогональным проектированием многоугольника на некоторую плоскость. Накопленный нами опыт преподавания стереометрии, частично отражённый в настоящей статье, показывает, что изучение такой темы как «Площадь ортогональной проекции многоугольника» повышает у школьников интерес к предмету, стимулирует освоение ими других серьёзных тем по геометрии, что в итоге ведёт к интенсификации всего процесса обучения.

1. Теорема о площади ортогональной проекции плоской фигуры

Параллельное проектирование, при котором проектирующие прямые перпендикулярны к плоскости проекций, называется ортогональным.

Ортогональной проекцией фигуры на данную плоскость называют множество точек пересечений с этой плоскостью перпендикулярных к ней прямых, проходящих через все точки этой фигуры. В общем случае справедлива следующая теорема.

Если фигура Ф с площадью SФ лежит в плоскости , а фигура Ф с площадью SФ является ортогональной проекцией фигуры Ф на плоскость , то имеет место равенство

SФ SФ cos ,

где – угол между плоскостями и .

В школьном курсе стереометрии приведённая теорема формулируется и доказывается лишь для случая, когда проектируемая фигура – плоский многоугольник. В этом случае формулировка имеет вид:

Площадь Sпр ортогональной проекции многоугольника на плоскость равна произве-

дению его площади Sмн , умноженной на косинус угла между плоскостью много-

угольника и плоскостью проекции: Sпр Sмн cos .

2. Применение теоремы о площади ортогональной проекции многоугольника при нахождении площадей сечений

Эту теорему с успехом применяют, прежде всего, при вычислении площадей сечений многогранников. Данный подход используется в ситуациях, когда нахождение площади Sпр ортогональной проекции многоугольника, полученного в сечении, и угла между

секущей плоскостью и плоскостью проектирования сопряжено с меньшими трудностями, чем непосредственное вычисление площади сечения. В этом случае

Sсечения	S	пр	.	(1)
cos

В примерах 1 – 4 иллюстрируется это основное применение теоремы о площади ортогональной проекции многоугольника.


	B1		C1	Пример 1. В правильной четырёхугольной призме
				сторона основания равна 4 см. Через диагональ основа-
A1		D1		ния под углом 45	к плоскости основания проведена
		M	плоскость, пересекающая боковое ребро. Найти пло-

				щадь сечения.
				Решение. Согласно условию задачи, площадь ор-
	B			тогональной проекции сечения на плоскость основания
	45	C	призмы равна половине его площади (см. рис. 1), т.е.

	O			42	8 (см2). Тогда, используя формулу (1), полу-
A	D		Sпр
	2
				чаем: Sсечения	Sпр	2

	Рис. 1				8 2 (см ).

cos45

Ответ: 82 см2.

Пример 2. Стороны основания прямого параллелепипеда равны 4 и 5, угол между ними равен 30°. Найти площадь сечения параллелепипеда плоскостью, пересекающей все его боковые рёбра и образующей с плоскостью основания угол в 45°.

	Решение. Для нахождения площади сечения воспользуемся формулой (1). Поскольку
	B1				C1	секущая плоскость пересекает все боковые рёбра
				прямого параллелепипеда ABCDA BC D , то ортого-
A1		D1			1	1	1	1
		N	нальной проекцией сечения MQNP является паралле-
	Q				лограмм ABCD (см. рис. 2). Отметим, что MQNP так-
					же является параллелограммом, так как MQ\|\|PN и
		P
M				MP\|\|QN по свойству параллельных плоскостей (если
B				C	две параллельные плоскости пересечены третьей, то
A	30	D			линии пересечения параллельны).
			Найдем площадь параллелограмма ABCD. Пусть,
	Рис. 2					для определённости, AB 4, AD 5,	BAD 30 ,
					тогда SABCD AB AD sin BAD 10.
			SABCD
	Поскольку SMQNP		, где 45 – угол между плоскостью сечения и основани-

				cos

ем параллелепипеда (на рис. 2 этот угол не показан), то SMQNP 102 .

Ответ: 102 .

Пример 3. Дан куб ABCDA1B1C1D1 с ребром, равным a. На рёбрах основания AB и AD взяты соответственно точки M и N так, что AM :MB 2:1 и AN :ND 2:1. Найти площадь сечения куба плоскостью, проходящей через точки M, N и C1 .

Решение. Приведём два способа решения этой задачи. Первый способ основан на разбиении многоугольника, полученного в сечении, на части и вычислении по отдельности площадей этих частей, а второй – на использовании теоремы о площади ортогональной проекции многоугольника. Читатель сам сможет определить, какой из предложенных подходов предпочтительнее.

Прежде чем перейти к решению задачи этими двумя способами, используя метод следов, построим сечение куба плоскостью, проходящей через точки M, N и C1. Соединим вначале точки M и N, поскольку они лежат в одной плоскости ABC (см. рис. 3а). Прямая MN лежит в плоскости ABC и пересекает прямые BC и DC в точках P и L соответственно.

Точка P принадлежит не только плоскости нижнего основания куба, но и плоскости грани BB1C1 (как и точка C1), поэтому, соединив P и C1, получим на ребре BB1 принадлежащую сечению точку F. Далее, точка L принадлежит не только плоскости нижнего основания куба, но и плоскости грани DD1C1 (как и точка C1), поэтому, соединив L и C1, получим на ребре DD1 принадлежащую сечению точку T. В завершение построения соединим в грани

AA1B1 точки M и F, а в грани AA1D1 точки T и N. Таким образом, сечением куба

ABCDA1B1C1D1 является пятиугольник MFC1TN .

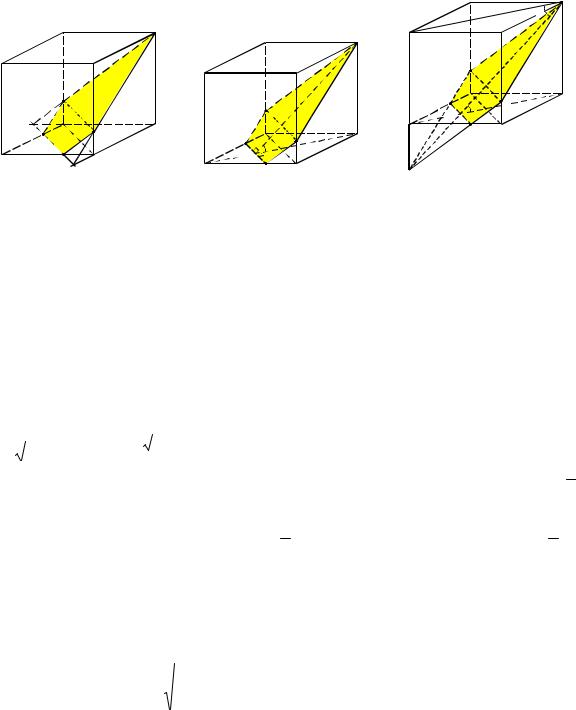
							B1		C1
	B1					A1		D1
		C1	B1
				C1

A1	D1
A1		D1		F

	F					M	B		C
P			F			T
B
		B		O		D
M	T		C	T	A	N
			M		C
A	N	D	A	O	D	A2
	L		N
	а				б		в
				Рис. 3

Первый способ решения. Проведём в пятиугольнике MFC1TN диагональ FT. Она ра-

зобьёт сечение на треугольник FC1T и четырёхугольник MFTN. Вычислим их площади по отдельности.

Найдем вначале площадь четырёхугольника MFTN. Поскольку MN || BD и BD лежит в плоскости BB1D1 , то MN || BB1D1 (по признаку параллельности прямой и плоскости). Так как секущая плоскость проходит через MN и пересекает плоскость BB1D1 по прямой TF, то TF ||MN (по теореме о линии пересечения). Далее, поскольку BD||MN и TF ||MN , то TF || BD. Следовательно, четырёхугольник MFTN – трапеция.

Из	прямоугольного треугольника AMN по теореме Пифагора находим
			2a	. Поскольку BF \|\| DT , как отрезки, расположенные на боко-
		2
MN	AM2 AN2

		3

вых рёбрах куба, то четырёхугольник BFTD – параллелограмм, а значит, TF BD a2 . Покажем, что трапеция MFTN – равнобедренная. Для этого рассмотрим вначале пря-

моугольный треугольник LDN. В нём ND a , LND 45 , следовательно, LD a . Да-

									3	3
лее, треугольники LDT и	LCC		подобны	с коэффициентом k	LD	1	. Поэтому

						1				LC 4
	CC1
DT		a	. Так как четырёхугольник BFTD – параллелограмм, то BF DT	a	, а зна-


4	4							4
чит, прямоугольные треугольники NDT и MBF равны по двум катетам. Поэтому, по тео-
реме Пифагора, NT MF	a	2		a	2	5a
							.
		12
					3		4

Далее находим длину h1 высоты этой равнобедренной трапеции MFTN. Опуская очевидные выкладки (читателю предлагается проделать их самостоятельно), получим


h			a 17		. Отсюда S	MFTN	TF MN	h	a 2 2a 2 3	a 17	5a2 34	.
	12		2	2			12		72
1					1
		Решим теперь задачу вычисления площади треугольника FC1T . Найдём в нём длины
сторон FC1 и TC1 . Для этого рассмотрим прямоугольные треугольники FB1C1	и TD1C1.

Они равны по двум катетам, поэтому по теореме Пифагора FC1 TC1 a	2	3a	2		5a
							,
			4
													4

т.е. треугольник FC1T – равнобедренный. Найдем длину h2 высоты этого треугольника. Опуская очевидные выкладки (читателю предлагается проделать их самостоятельно), по-


		a 17									TF h			1				a	17			a2 34

лучим h				. Отсюда S	FC T			2				a	2							.

2		4							2				2					4			8
						1

Наконец, площадь всего сечения:
						5a2					a2				7a2								7a2
SMFC TN SMFTN	S FC T		34				34			34		.				Ответ:	34	.

1			1			72					8						36							36

Второй способ решения. Для нахождения площади сечения воспользуемся формулой (1). Ортогональной проекцией пятиугольника MFC1TN на плоскость ABC служит многоугольник MBCDN (см. рис. 3б). Найдём площадь MFC1TN . Очевидно, что SMBCDN SABCD S AMN . Треугольник AMN – прямоугольный. Длины его катетов AM и

AN, согласно условию задачи, равны

. Поэтому SMBCDN a

7a2

2 3

Далее, проведём в квадрате ABCD диагонали BD и AC. Равнобедренные прямоуголь-

ные

треугольники

AMN

ABD

подобны

с коэффициентом

. Тогда

OC AC AO

. Кроме того, поскольку MN || BD и BD AC ,

то MN OC.

Соединим точки O и C1. Тогда OC1

– наклонная к плоскости ABC, OC – проекция на-

клонной

OC1

и MN OC.

Следовательно, по

теореме

трёх

перпендикулярах,

MN OC1 . Значит,

COC1

– линейный угол двугранного угла CMNC1 .

Вычислим теперь косинус угла между плоскостью сечения и нижним основанием куба. Для этого рассмотрим прямоугольный треугольник CC1O . По теореме Пифагора

			a 17	. Откуда cos	OC	2	2	.
OC	OC2 CC2

1	1	3		OC1	17

Поскольку, согласно теореме о площади ортогональной проекции многоугольника,


SMFC TN	S	MBCDN	, то окончательно получим: SMFC TN	7a	2		17			7a2 34
									.
	cos
1		1	9			2 2		36

Замечание. При решении задачи вторым способом для нахождения cos можно до-

строить секущую плоскость до её пересечения с продолжением ребра AA1 за точку A (см.

рис. 3в). Тогда cos	SA BC D
	1 1 1 1	.

	SA MFC TN
2	1

Пример 4. Дан куб ABCDA1B1C1D1 с ребром, равным a. Точка M – середина ребра AD,

точка N – середина ребра C1D1 . Найти площадь сечения куба плоскостью, проходящей через точки M, N и C.

Решение. Построим сечение куба плоскостью, проходящей через точки M, N и C. Соединим вначале точки M и C, поскольку они лежат в одной плоскости ABC. Затем соединим точки C и N, так как они лежат в одной плоскости DD1C1 (см. рис. 4). Прямые СN и

DD1 лежат в плоскости DD1C1	и не параллельны. Значит, они пересекаются в точке Q.
Точка Q принадлежит не только плоскости DD1C1, но и плоскости грани AA1D1 (как и
точка M),	поэтому,	соединив M и Q, получим на ребре A1D1 принадлежащую сечению
точку P. В завершение построения соединим в верхней грани куба точки P и N.
			Q	Отметим, что плоскости оснований куба парал-
			лельны друг другу. Значит, по свойству параллель-
				ных плоскостей (если две параллельные плоскости
				пересечены третьей, то линии пересечения парал-
		B1	C1	лельны) MC\|\| PN . Далее, поскольку прямые MP и
		CN пересекаются в точке Q, то стороны MP и CN че-
A1		P	N	тырёхугольника MPNC не параллельны. Таким обра-
	D1	зом, сечением куба ABCDA1B1C1D1 является трапеция

			MPNC.

				Для нахождения площади сечения воспользуемся
				формулой (1). Построим вначале линейный угол дву-
		BO	C	гранного угла DMCQ. Для этого в прямоугольном
		треугольнике MCD опустим перпендикуляр DO к ги-
			N1	потенузе MC. Соединим точки O и Q. Тогда QO – на-
A	M	P1 D	клонная к плоскости ABC, DO – проекция наклонной
				QO и MC DO.	Следовательно, по теореме о трёх
		Рис. 4		перпендикулярах,	MC QO. Значит, QOD –
				линейный угол двугранного угла DMCQ.

Вычислим теперь косинус угла между плоскостью сечения и нижним основанием куба. Для этого рассмотрим вначале прямоугольный треугольник MCD. По теореме Пифа-

a 5

. Для нахождения высоты DO выразим пло-

гора MC

MD2 DC2

щадь S MCD

двумя способами:

MD DC

MC DO

S MCD

, S MCD

DO.

DO. Отсюда DO

Тогда, приравняв их, получим

Далее, рассмотрим прямоугольные треугольники CDQ и ND1Q. У этих треугольников острый угол при вершине Q – общий. Значит, они подобны. Поскольку, согласно условию

задачи, точка N –

середина ребра C1D1, то коэффициент подобия треугольников CDQ и

ND1Q равен 2. Отсюда, очевидно, что DQ 2a.

Рассмотрим,

наконец,

прямоугольный треугольник QOD. По теореме Пифагора

QO DQ

. Откуда cos

Построим теперь четырёхугольник MP1N1C, являющийся ортогональной проекцией трапеции MPNC на плоскость ABC. Так как PN лежит в плоскости, построенной на парал-

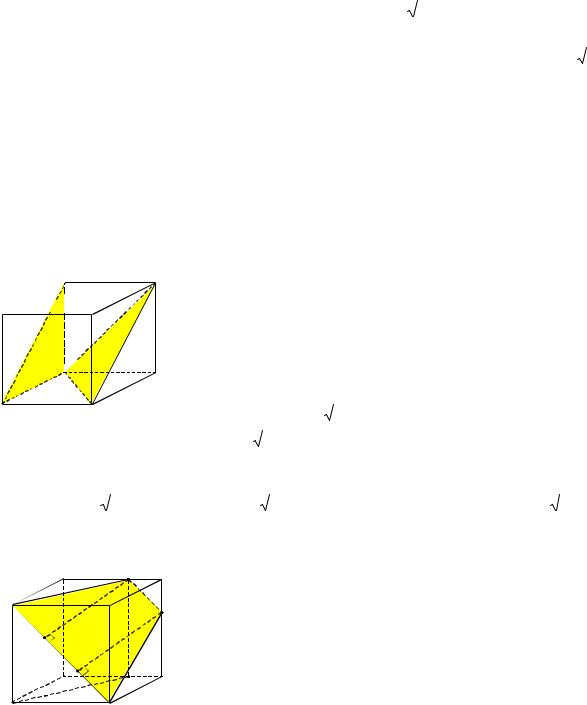
лельных прямых PP1 и NN1,

и параллельна плоскости ABC,

то линия пересечения

P1N1

плоскостей ABC и PNN1

параллельна PN (по теореме о линии пересечения). Поскольку

P1N1 || PN и MC|| PN , то P1N1 ||MC, а значит, четырёхугольник MP1N1C – трапеция.

Найдём площадь трапеции MP1N1C. Очевидно, что SMPN C S

MCD

S PN D . Прямо-

угольные треугольники MCD и P1N1D подобны, так как P1N1D MCD (как соответст-

венные). Точка

N1 – середина ребра CD, значит,

коэффициент подобия треугольников

MCD и PN

D равен 2. Поэтому S

MPN C

MCD

3a2

1 1

Согласно

теореме

площади

ортогональной

проекции

многоугольника,

SMP1N1C

3a2

SMPNC

, откуда окончательно получим: SMPNC

cos

3a2

Ответ:

3. Применение теоремы о площади ортогональной проекции многоугольника при вычислении угла между плоскостями

Кроме рассмотренного основного применения теоремы о площади ортогональной проекции многоугольника её можно также использовать при вычислении угла между плоскостью сечения и плоскостью какой-либо грани многогранника (обычно в качестве такой грани выступает основание пирамиды или призмы). Так поступают в случаях, когда нахождение Sпр и Sсечения является более простой задачей, чем непосредственное вычисление двугранного угла , сопряжённое с построением на чертеже его линейного угла.

A1 D1

A D

Рис. 5

Из формулы о

Пример 5. В кубе

ABCDA1B1C1D1 найти угол между

плоскостью грани AA1B1B и плоскостью BC1D.

Решение. Пусть ребро куба равно a. Ортогональной

проекцией треугольника BC1D является треугольник AB1B

(см. рис. 5), площадь

которого равна

Поскольку

BD BC1

C1A a

(как диагонали

граней

куба), то

a2 .

S BC D

площади ортогональной проекции многоугольника получим:

S AB B

. Отсюда arccos

Ответ: arccos

S BC D

Пример 6. В кубе

ABCDA1B1C1D1 через его вершины

A , D и точку M, расположенную на ребре CC

так, что

CM :MC1 2:1, проведено сечение. Найти угол наклона

секущей плоскости к плоскости основания ABCD.

Решение. Построим сечение куба плоскостью, прохо-

дящей через точки A1, D и M. Соединим вначале точки A1

и D, поскольку они лежат в одной плоскости DD A . Затем

Dсоединим точки D и M, так как они лежат в одной плоскости DD1C1 (см. рис. 6). Противоположные боковые грани

Рис. 6	DD1A1	и CC1B1 в кубе параллельны. Поэтому секущая

плоскость, согласно свойству параллельных плоскостей (если две параллельные плоскости пересечены третьей, то линии пересечения параллельны) будет пересекать грань CC1B1 по прямой MP так, что MP|| A1D . Наконец, соединим точки A1 и P, так как они лежат в одной плоскости A1B1C1. Поскольку A1P и DM не параллельны, то четырёхуголь-

ник A1PMD, являющийся сечением куба, – трапеция.

Ортогональной проекцией трапеции A1PMD плоскости основания ABCD является прямоугольная трапеция ALCD. Для определения угла наклона секущей плоскости к

плоскости основания ABCD воспользуемся формулой cos SALCD . Для этого найдем

SA1PMD

площади указанных трапеций.

Пусть ребро куба равно a. Тогда, согласно условию задачи, MC a . Кроме того,
1	3

очевидно, что A1D a2. Поскольку MP|| A1D и DD1 ||MC1, то A1DD1 PMC1 (как углы с соответственно сонаправленными сторонами). Поэтому прямоугольные треуголь-

ники A DD и PMC подобны с коэффициентом k	1	. Следовательно, MP	A1D		a 2

1	1							1																						3						3	3
	A1D1			a
и PC		.

1	3	3
																										2a
Далее,	так как	A B DC a, B P CM		,				то		прямоугольные	треугольники

										1	1												1				3
A1B1P			DCM
и		равны				по			двум		катетам.		Поэтому			по		теореме		Пифагора

		4a2				a						.
A P DM a2			13

1								9							3

Следовательно, трапеция A1PMD равнобедренная. Найдём её высоту. Для этого опус-
тим из	точек P	и				M		перпендикуляры		PQ и					MK		на			основание A1D. Тогда
	A1D MP			a			. Отсюда по теореме Пифагора из прямоугольного треуголь-
AQ DK		2

1		2							3

																																				13a2		2a2		a	.
																																						11
ника A PQ высота трапеции A PMD равна:	PQ					A P2		AQ2

1																				1												1		1	9	9			3

																											A D MP				2a2	22
Таким образом, площадь сечения: SAPMD		1							PQ									.
			2								9
																						1
																																				a
В прямоугольной трапеции ALCD основания равны AD a	и LC PC	,		а высота
3
																								AD LC				2a2					1
DC a . Тогда её площадь:		SALCD	DC	.
		2					3

Подставляя полученные значения площадей в формулу, находим
																					S					2a	2	2a2	3
														cos		ALCD	:	22	22		.
															SAPMD	3	9							22

																						1
	3																								Ответ: arccos	3		.
Следовательно, arccos	22		.																					22

															22																					22

Пример 7. Плоскость пересекает прямоугольный параллелепипед с квадратным основанием по ромбу с острым углом . Под каким углом эта плоскость пересекает боковые рёбра параллелепипеда?

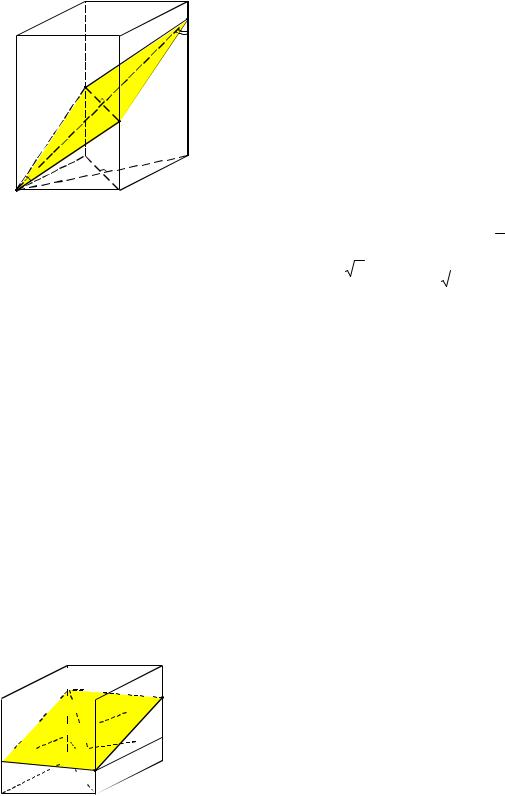
Решение. Без ограничения общности рассуждений будем считать, что секущая плоскость проходит через вершину A нижнего основания параллелепипеда, пересекая его бо-

ковые рёбра BB1, CC1	и DD1	в точках M, N и P соответственно (см. рис. 7).
	B1		C1	Рассмотрим прямоугольные треугольники AMB и
		D1		N	APD. В них AM AP , т.к., согласно условию, AMNP –
A1			ромб. Кроме того, AB AD как стороны основания
		x		параллелепипеда ABCD, являющегося квадратом. Сле-

			x		довательно, AMB APD по гипотенузе и катету, а
	M			значит, MB PD.
		O			Рассмотрим теперь четырёхугольник BMPD. В нём
x		P			противоположные стороны MB и PD параллельны и
	x B	a			равны, значит, BMPD – параллелограмм (отметим до-
		C	полнительно, что BMPD – прямоугольник). Отсюда
	a		a	MP\|\| BD и MP BD.
A	a	D			Пусть сторона ромба AMNP равна x, а ребро осно-
	Рис. 7			вания параллелепипеда равно a. Тогда SAMNP x2 sin ,

SABCD a2 . Поскольку MP BD a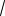2, то из прямо-

угольного треугольника AOP имеем: sin

a 2

, или a x

sin

Вычислим косинус угла между секущей плоскостью и основанием:

SABCD

2x2 sin2

cos

SAMNP

x2 sin

Обозначим через угол,

x2 sin

под которым секущая плоскость пересекает боковые рёбра

параллелепипеда. Поскольку

, то

cos cos

sin . Значит,

sin tg

Отсюда arcsin tg


						Ответ: arcsin tg	.

								2
	Пример 8. В кубе ABCDA1B1C1D1 с ребром, равным a, через точки M, P и N на рёбрах
BB , CC и DD соответственно, такие, что BM	3a	, CP	2a	и DN	a	, проведена се-
1	1	1	4	3	4

кущая плоскость. Найти угол между плоскостью сечения и плоскостью основания куба.

Решение. Построим сечение куба плоскостью, проходящей через точки M, P и N. Соединим вначале точки M и P, поскольку они лежат в одной плоскости BB1C1 . Затем соединим точки P и N, т.к. они лежат в одной плоскости

DD1C1 (см. рис. 8).

Противоположные боковые грани AA1D1 и BB1C1 в кубе параллельны. Поэтому секущая плоскость, согласно свойству параллельных плоскостей (если две параллельные плоскости пересечены третьей, то линии пересечения параллельны) будет пересекать грань AA1D1 по прямой NQ так, что

NQ|| MP.

Соединим точки M и Q, т.к. они лежат в одной плоскости AA1B1. Тогда MQ|| NP по

тому же свойству параллельных плоскостей AA1B1

CC1D1 . Таким образом,

сечение

представляет собой параллелограмм MPNQ.

Вычислим площадь MPNQ и, поскольку квадрат ABCD – ортогональная проекция

MPNQ, определим косинус угла между плоскостью сечения и плоскостью ABC.

Найдём стороны треугольника MNP. Используя теорему Пифагора, получим:

из прямоугольного треугольника MLP (ML CC1 )

145

MP (LC PC)2 MC2

144

из прямоугольного треугольника NPS (NS CC1)

25a2

13a

(PC SC)2 NS2

из прямоугольного треугольника MNK (KN BB1)

144

2a2

(BM BK)2 KN2

Полупериметр треугольника MNP равен p

31)

. Используя формулу Герона,

145

найдём его площадь:

SMNP

170

. Следовательно,

SMPNQ 2SMNP

170

. Из фор-

SABCD

мулы для

площади

ортогональной

проекции получим: cos

. Отсюда

SMPNQ

170

arccos

170

Ответ: arccos

170

4. Применениетеоремы о площади ортогональной проекции многоугольника при вычислении площади боковой поверхности пирамиды

Ещё одной известной задачей, при решении которой применяется теорема о площади ортогональной проекции многоугольника, является задача вычисления площади Sбок бо-

ковой поверхности пирамиды, у которой все боковые грани одинаково наклонены к плоскости её основания (под углом ), или вершина пирамиды лежит на перпендикуляре, восставленном из центра вписанной в её основание окружности. Тогда

Sбок	Sосн	.	(2)

	cos

Пример 9. Стороны основания треугольной пирамиды равны 6 см, 10 см и 14 см. Каждый двугранный угол при её основании равен 30°. Найти площадь боковой поверхности пирамиды.

Решение. Для нахождения площади сечения воспользуемся формулой (2). Найдём вначале площадь основания треугольной пирамиды, воспользовавшись формулой Герона. Поскольку полупериметр треугольника в основании равен 15 см, то

Sосн 15 (15 6) (15 10) (15 14) 153 (см2).

Тогда Sбок		Sосн	3	2
	15 3:	30
		(см ).
cos30	2

Ответ: 30 см2.

Пример 10. Боковые грани пирамиды, в основании которой лежит ромб, наклонены к плоскости основания под углом 30°. Диагонали ромба равны 10 см и 24 см. Найти площадь боковой поверхности пирамиды.

Решение. Для нахождения площади сечения воспользуемся формулой (2). Поскольку боковые грани пирамиды SABCD наклонены к основанию ABCD под одинаковым углом, то её вершина S проектируется в центр вписанной в ромб окружности, т. е. в точку O пересечения его диагоналей (см. рис. 9). Тогда

SABCD AC BD 120 (см2). 2

Следовательно, Sбок SABCD 803 (см2). cos30

Ответ: 803 см2.

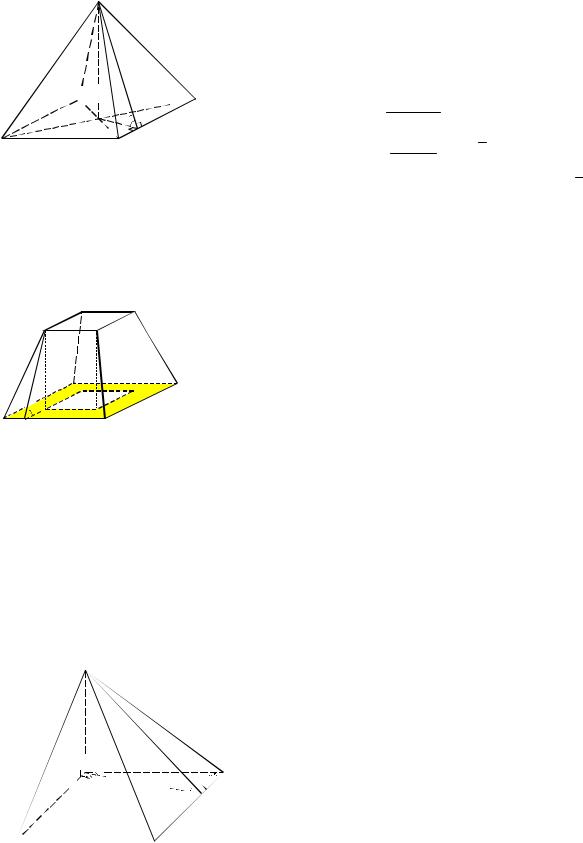
Пример 11. В правильной усечённой четырёхугольной пирамиде стороны нижнего и верхнего оснований равны соответственно a и b (a b). Найти площадь полной поверхности усечённой пирамиды, если её боковые грани наклонены к плоскости основания под углом .

Решение. Поскольку основаниями правильной усе-

чённой четырёхугольной пирамиды являются квадраты со

сторонами a и b, то сумма их площадей равна

a2 b2 .

Очевидно, что ортогональная проекция боковой поверхно-

сти усечённой пирамиды на плоскость нижнего основания

представляет собой квадрат со стороной a, из которого

«вырезан» квадрат со стороной b. При этом стороны «вы-

Рис. 10

резанного» квадрата параллельны сторонам нижнего осно-

вания пирамиды (см. рис. 10). Так как боковые грани усе-

чённой пирамиды наклонены к плоскости основания под

одинаковым углом , то площадь её боковой поверхности равна: Sбок

Sпр

cos

Таким образом, S

полн a

a2 b2

Ответ: a

a2 b2

cos

Пример 12. Основанием пирамиды является ромб. Две боковые грани перпендикулярны к плоскости основания и образуют двугранный угол в 120°, а две другие боковые грани наклонены к плоскости основания под углом 30°. Найти площадь поверхности пирамиды, если её высота равна 12.

Решение. Площадь полной поверхности пирамиды равна сумме площадей боковых граней и основания, т. е.

Sполн SASB SBSC SASD SDSC SABCD .

Положим, что сторона ромба ABCD равна a. C Пусть боковые грани ASB и BSC пирамиды

SABCD перпендикулярны к плоскости основания ABCD (см. рис. 11). Тогда боковое ребро SB пирамиды перпендикулярно к плоскости ромба и равно высоте, а боковые грани ASB и BSC пирамиды являются равными прямоугольными треугольниками

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Скачать материал

без ожидания

Скачать материал

без ожидания

Сейчас обучается 249 человек из 63 регионов

Сейчас обучается 140 человек из 50 регионов

Описание презентации по отдельным слайдам:

1 слайд

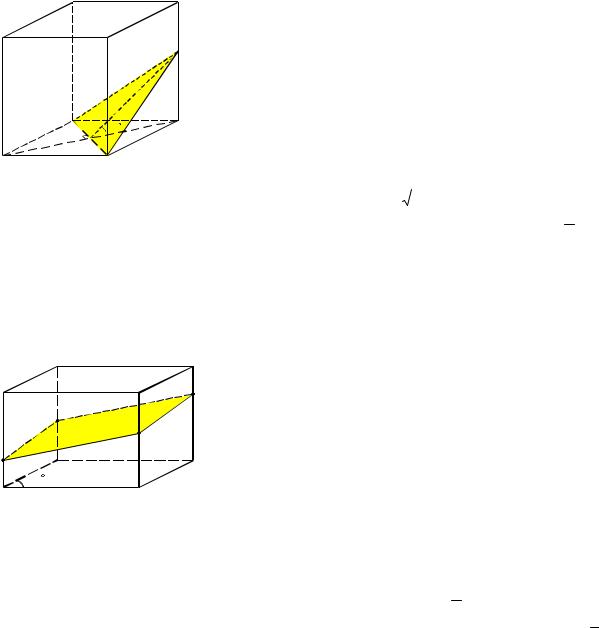
Изобразите сечение единичного куба A…D1, проходящее через вершины A, B, C1. Найдите его площадь.
Ответ. .
2 слайд

Изобразите сечение единичного куба A…D1, проходящее через середины ребер AB, BC, A1B1. Найдите его площадь.
Ответ. .
3 слайд

Изобразите сечение единичного куба A…D1, проходящее через вершину A и середины ребер CD, C1D1. Найдите его площадь.
Ответ. .
4 слайд

Изобразите сечение единичного куба A…D1, проходящее через вершину A и середины ребер BB1, DD1. Найдите его площадь.
Ответ. .
5 слайд

Изобразите сечение единичного куба A…D1, проходящее через вершины A, C и середину ребра С1D1. Найдите его площадь.
Решение. Сечением является равнобедренная трапеция ACEF.
Ее основания AC и EF равны
Высота FH равна
Площадь сечения равна
6 слайд

Изобразите сечение единичного куба A…D1, проходящее через середины ребер AB, BC, CC1. Найдите его площадь.
Ответ. .
7 слайд

Изобразите сечение единичного куба A…D1, проходящее через вершину A и середины ребер BC, DD1. Найдите его площадь.
Решение. Сечением является трапеция AEFG.
Ее основания AG и EF равны соответственно и .
Для нахождения ее высоты EH рассмотрим равнобедренный треугольник AEG, в котором AE = AG = , EG = . Высота, опущенная на сторону EG равна . Следовательно, высота EH равна . Площадь сечения равна .
8 слайд

Изобразите сечение единичного куба A…D1, проходящее через вершину D1 и середины ребер AB, BC. Найдите его площадь.
Решение. Сечением является пятиугольник EFGD1H.
Площадь сечения равна
Его плоскость образует с плоскостью грани ABCD угол, косинус которого равен
Площадь пятиугольника AEFCD
равна
Можно было бы найти площадь пятиугольника как разность площади треугольника PQD1 и суммы площадей треугольников PEH, FQG.
Высота D1R треугольника PQD1 равна . Сторона PQ равна .
Площадь треугольника PQD1 равна . Площади треугольников PEH, FQG в 9 раз меньше площади треугольника PQD1.
Следовательно, площадь пятиугольника равна
9 слайд

Изобразите сечение единичного куба A…D1, проходящее через середины ребер AB, BC, DD1. Найдите его площадь.
Ответ. .
10 слайд

Изобразите сечение тетраэдра ABCD, все ребра которого равны 1, проходящее через середины ребер AB, BC и CD. Найдите его площадь.
Ответ. 0,25.
11 слайд

Изобразите сечение пирамиды SABCD, все ребра которой равны 1, проходящее через середины ребер SA, SB и SC. Найдите его площадь.
Ответ. 0,25.
12 слайд

Изобразите сечение пирамиды SABCD, все ребра которой равны 1, проходящее через вершины B, D и середину ребра SC. Найдите его площадь.
Площадь сечения равна
Решение. Сечением является равнобедренный треугольник BDE.
BD = , высота EO равна 0,5.
13 слайд

Изобразите сечение пирамиды SABCD, все ребра которой равны 1, проходящее через вершины A, B и середину ребра SC. Найдите его площадь.
Решение. Сечением является равнобедренная трапеция ABEF.
Площадь сечения равна
Ее основания AB и EF равны соответственно 1 и 0,5,
высота EH равна
14 слайд

Изобразите сечение пирамиды SABCD, все ребра которой равны 1, проходящее через середины ребер AD, BC и SC. Найдите его площадь.
Ответ. .
15 слайд

Изобразите сечение пирамиды SABCD, все ребра которой равны 1, проходящее через вершину A и середины ребер SB и SD. Найдите его площадь.
Площадь сечения равна
Его диагонали AF и GE которого перпендикулярны и равны соответственно
Решение. Сечением является четырехугольник AEFG,
16 слайд

Изобразите сечение пирамиды SABCD, все ребра которой равны 1, проходящее через вершину B, середину ребра SD и параллельное прямой AC. Найдите его площадь.
Площадь сечения равна
Решение. Сечением является четырехугольник AEFG, диагонали BF и GE которого перпендикулярны и равны соответственно
17 слайд

Изобразите сечение пирамиды SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, проходящее через середины ребер SA, SB, SC. Найдите его площадь.
Ответ.
18 слайд

Изобразите сечение пирамиды SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, проходящее через вершины A, F и середину ребра SC. Найдите его площадь.
Решение. Сечением является шестиугольник AB1C1D1E1F.
Следовательно, площадь сечения равна
Его площадь равна площади трапеции A1C1D1F1 минус удвоенная площадь треугольника AA1B1.
Площадь трапеции равна
Стороны основания трапеции равны 3 и 0,5. Высота AC1 равна
Высота треугольника AA1B1, опущенная на сторону AA1, равна
Его площадь равна
19 слайд

Изобразите сечение правильной треугольной призмы ABCA1B1C1, все ребра которой равны 1, проходящее через середины ребер AA1, BB1, CC1. Найдите его площадь.
Ответ. 0,5.
20 слайд

Изобразите сечение правильной треугольной призмы ABCA1B1C1, все ребра которой равны 1, проходящее через вершины B, B1 и середину ребра AC. Найдите его площадь.
Ответ. .
21 слайд

Изобразите сечение правильной треугольной призмы ABCA1B1C1, все ребра которой равны 1, проходящее через вершины A, B и середину ребра A1C1. Найдите его площадь.
Ответ. .
22 слайд

Изобразите сечение правильной треугольной призмы ABCA1B1C1, все ребра которой равны 1, проходящее через середины ребер AB, BC и CC1. Найдите его площадь.
Ответ. .
23 слайд

Изобразите сечение правильной треугольной призмы ABCA1B1C1, все ребра которой равны 1, проходящее через середины ребер AB, AA1 и A1C1. Найдите его площадь.
Сторона PQ треугольника PQF равна .
Высота FG равна . Его площадь равна
Площадь сечения равна
Площади треугольников D1E1P и DEQ равны
Решение. Сечением является пятиугольник DEE1D1F.
Соединим точку F с серединой G отрезка EE1. Площадь пятиугольника равна разности площади треугольника PQF и суммы площадей треугольников D1E1P и DEQ.
24 слайд

Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, проходящее через вершины A, C и C1. Найдите его площадь.
Ответ. .
25 слайд

Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, проходящее через вершины A, D и D1. Найдите его площадь.
Ответ. 2.
26 слайд

Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, проходящее через середины ребер BC, EF и B1C1. Найдите его площадь.
Ответ. .
27 слайд

Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, проходящее через середины ребер AB, BC и A1B1. Найдите его площадь.
Ответ. .
28 слайд

Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, проходящее через середины ребер AB, CD и A1B1. Найдите его площадь.
Ответ. 1,5.
29 слайд

Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, проходящее через вершины D, D1 и середину ребра EF. Найдите его площадь.
Ответ. .
30 слайд

Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, проходящее через вершины A, A1 и середину ребра CD. Найдите его площадь.
Ответ. .
31 слайд

Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, проходящее через вершины A, C и D1. Найдите его площадь.
Ответ. .
32 слайд

Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, проходящее через вершины A, D и C1. Найдите его площадь.
Ответ. .
33 слайд

Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, проходящее через вершины A, B и D1. Найдите его площадь.
Решение. Сечением является шестиугольник.
Его плоскость образует угол с плоскостью ABC, косинус которого равен
Площадь основания призмы равна
Площадь сечения равна 3.
34 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, B, C1. Найдите его площадь.
Ответ. .
35 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, B, C2. Найдите его площадь.
Ответ. .
36 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A1, С2, D2. Найдите его площадь.
Ответ. .
37 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, A2, C2. Найдите его площадь.
Ответ. .
38 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, C, C1. Найдите его площадь.
Ответ. .
39 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины B, B1, D1. Найдите его площадь.
Ответ. .
40 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины B, B1, D2. Найдите его площадь.
Ответ. .
41 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины D, B2, D2. Найдите его площадь.
Ответ. .
42 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A1, C, C1. Найдите его площадь.
Ответ. .
43 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины B, C, D2. Найдите его площадь.
Ответ. .
44 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины B, C, C2. Найдите его площадь.
Ответ. .
45 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины B1, C1, D2. Найдите его площадь.
Ответ. .
46 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, B и C3. Найдите его площадь.
Ответ. .
47 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, B и C2. Найдите его площадь.
Ответ. .
48 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A1, B1 и C3. Найдите его площадь.
Ответ. .
49 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, B и B3. Найдите его площадь.
Ответ. .
50 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, C и B3. Найдите его площадь.
Ответ. .
51 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, B и C2. Найдите его площадь.
Ответ. .
52 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, B и C3. Найдите его площадь.
Ответ. .
53 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, A1, D2. Найдите его площадь.
Ответ. .
54 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, A1, C2. Найдите его площадь.
Ответ. 3.
55 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины B, A2, C2. Найдите его площадь.
Ответ. 3.
56 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины A, B и C1. Найдите его площадь.
Ответ. .
57 слайд

Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы которого прямые, проходящее через вершины B, C и D1. Найдите его площадь.
Ответ. .

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 256 044 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

23.10.2015
560
0

23.10.2015
504
0

23.10.2015
466
0

Рейтинг:
3 из 5

23.10.2015
11373
79

23.10.2015
1094
0

23.10.2015
741
1

23.10.2015
558
0

Вам будут интересны эти курсы:

Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Источник

Решение:

Пусть сторона куба равна а. В сечении получилась равнобедренная трапеция. Найдём основание DB по теореме Пифагора:

DB=sqrt{a^{2}+a^{2}}=sqrt{2a^{2}}=asqrt{2}

Найдём основание MN по теореме Пифагора:

MN=sqrt{(frac{a}{2})^{2}+(frac{a}{2})^{2}}=sqrt{frac{a^{2}}{4}+frac{a^{2}}{4}}=sqrt{frac{2a^{2}}{4}}=sqrt{frac{a^{2}}{2}}=frac{a}{sqrt{2}}

Найдём DM по теореме Пифагора:

DM=sqrt{a^{2}+(frac{a}{2})^{2}}=sqrt{frac{5a^{2}}{4}}=frac{sqrt{5}a}{2}

Зная что трапеция DMNB равнобедренная найдём DO:

DO=frac{asqrt{2}-frac{a}{sqrt{2}}}{2}=frac{frac{2}{sqrt{2}}}{2}=frac{a}{2sqrt{2}}

Найдём высоту MO по теореме Пифагора:

MO=sqrt{(frac{sqrt{5}a}{2})^{2}-(frac{a}{2sqrt{2}})^{2}}=sqrt{frac{5a^{2}}{4}-frac{a^{2}}{8}}=sqrt{frac{9a^{2}}{8}}=frac{3a}{2sqrt{2}}

Площадь трапеции DMNB равна:

S_{DMNB}=frac{asqrt{2}+frac{a}{sqrt{2}}}{2}cdot frac{3a}{2sqrt{2}}=frac{frac{3a}{sqrt{2}}cdot 3a}{4sqrt{2}}=frac{9a^{2}}{8}

По условию она равна 2021·3:

frac{9a^{2}}{8}=2021cdot 3\3a^{2}=2021cdot 8\a^{2}=frac{2021cdot 8}{3}

Найдём площадь полной поверхности куба:

S=6a^{2}=6cdot frac{2021cdot 8}{3}=2cdot 2021cdot 8=32336

Ответ: 32336.

Источник

Площадь диагонального сечения куба очень легко найти, если известна величина его ребра или площадь одной грани.

Если известна величина ребра куба, тогда площадь сечения находим по формуле

S(диагонального сечения) = 1,414*а*а*

Если известна площадь одной из граней куба, тогда формула площади сечения куба будет выглядеть так

S(диагонального сечения) = 1,414*S(грани куба)

Примечание – для удобства вместо корень из двух написано его числовое значение округленное до тысячных.

модератор выбрал этот ответ лучшим

Степан-16
[34.5K]

5 лет назад

Осевым сечением куба будет прямоугольник, одна сторона которого равна длине ребра, а другая – диагонали грани. Если ребро известно и равно а. То диагональ грани будет одновременно гипотенузой равностороннего прямоугольного треугольника, катеты которого – это два смежных ребра куба или две стороны квадрата грани. Отсюда диагональ (гипотенузу) можно вычислить по теореме Пифагора или отношением длина ребра а к синусу (или косинусу) 45град (половины прямого угла). Синус 45град равен половине кв. корня из 2, или 0.707. Поэтому диагональ b = a/0.707. И площадь диагонального сечения квадрата:

S = а*b = (а^2)/0.707

(где а^2 – это а в квадрате, или во второй степени).

Ксарфакс
[156K]

4 года назад

Куб – это правильный многогранник, у которого каждая грань (всего их 6) является квадратом и все ребра равны между собой.

Диагональное сечение куба – это прямоугольник, у него меньшая сторона совпадает с ребром, а большая – с диагональю грани (основания).

Таким образом, чтобы найти площадь диагонального сечения куба, нужно воспользоваться формулой площади прямоугольника: S(пр) = a * b.

Пусть ребро куба равно a.

Тогда длину диагонали основания можно высчитать с помощью теоремы Пифагора. Это гипотенуза в прямоугольном треугольнике, у которого катеты равны между собой. Длина диагонали будет равняться a√2.

Получаем формулу площади диагонального сечения:

Нужно возвести ребро куба в квадрат и умножить полученное значение на √2 (корень из 2 равен приблизительно 1,41).

Пример

Если длина ребра куба составляет 10 см, то площадь сеч. будет такой:

S = a²√2 ≈ 10 * 10 * 1,41 = 141 см.

Марина Вологда
[295K]

4 года назад

Если в условии задачи необходимо найти площадь диагонального сечения куба, значит нам известно либо площадь одной грани или величина его ребра.

Формула для нахождения площади диагонального сечения куба с известной величиной ребра: S=а*a * квадратный корень из 2 (где a – величина ребра).

Пример:

Длина ребра куба равна 5 см, высчитываем площадь сечения:

S = axa умноженное на квадратный корень из 2 = 5 х 5 х 1,41 = 35,25 см.

А вот здесь один из примеров решения по нахождению площади диагонального сечения куба:

А вот еще одно решение, которое Вам поможет разобраться и подставить в формулу значения:

Нахождение площади диагонального сечения куба задача не сложная, ведь у куба все его стороны равны между собой, а грани представляют собой квадраты. Поэтому если построить сечение куба проходящее через диагонали противоположных граней мы получим прямоугольник, у которого меньшие стороны кажутся равными стороне куба, пусть это классически будет А, а большие стороны будут равны диагоналям квадрата со стороной А.

Формула для нахождения диагоналей квадрата вот:

D=a*√2

Площадь прямоугольника – это произведение его сторон и тогда формула площади диагонального сечения куба принимает вид:

S=D*a

Или:

S=а*a*√2

Бархатные лапки
[382K]

4 года назад

Куб – это геометрическая фигура, правильный многогранник, все его грани (а их шесть) представляют собой квадраты.

Диагональное сечение куба представляет собой прямоугольник, меньшая из сторон будет равняться длине ребра куба, а другая сторона равняется – диагонали грани.

Для начала нам нужно найти площадь прямоугольника, ее можно найти по формуле:

S(пр) = a * b.

Ребро обозначим – а. Другую сторону прямоугольника (б) можно вычислить по формуле Пифагора.

Тогда у нас получается длина диагонали – a√2.

Далее выводим формулу площади диагонального сечения – S=а*a*√2.

Рассчитаем площадь диагонального сечения куба на примере:

Допустим у нас длина ребра – 4 см.

Подставляем по формуле: 4*4*1,41=22,56.

IrinaKn
[8.3K]

9 лет назад

Если я правильно поняла, при диагональном сечение вы получите поверхность – прямоугольник, две стороны которого будут равные сторонам куба, а другие две – диагонали на любой из поверхностей куба (т.е. любого квадрата).

Т.о., если у куба сторона = а, то вы получите прямоугольник со сторонами а и а*корень из 2

Т.о. искомая площадь = а*(а * корень из 2)= (а в квадрате) * (корень из 2).

Помощни к
[56.9K]

6 лет назад

Достаточно узнать длину любого ребра объемной фигуры, в которой находится диагональное сечение.

Если найдете длину ребра, то сможете найти площадь по формуле: длина ребра в квадрате помножить на корень двух.

Вот формула:

Валерий Альбертович
[7K]

4 года назад

Площадь диагонального сечения куба можно найти несколькими способами, в зависимости от того, какие данные нам известны.

Если в нашем распоряжении информация о площади одного из граней куба, то диагональное сечение куба будет находиться по формуле: S (диагонального сечения) = S (грани куба) * √2

Если же в нашем распоряжении информация о величине ребра куба, то в таком случае формула будет выглядеть так: S (диагонального сечения) = a² * √2

88SkyWalker88
[428K]

4 года назад

Чтобы найти площадь диагонального сечения куба, необходимо воспользоваться формулой: S=а*a*√2

S – так обозначается площадь.

а – это сторона куба (ее значение нам известно).

√2 равно 1,41.

Предположим, что по условию задачи сторона куба (то есть а) равна 5.

Подставляем в формулу:

S=5*5*1,41=25*1,41=35,25

Знаете ответ?

Источник

Описание презентации по отдельным слайдам:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Другие материалы

Вам будут интересны эти курсы:

S = а*b = (а^2)/0.707

Вам также может понравиться

Как исправить искривление позвоночника корсет

Как найти яндекс переводчик на эмодзи

Как найти home на клавиатуре

Добавить комментарий Отменить ответ