Как найти площадь сечения в паралелипипеде

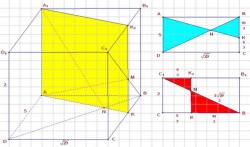
Площадь диагонального сечения параллелепипеда

У прямоугольного параллелепипеда диагональное сечение представляет собой прямоугольник.

Значит, для нахождения его площади нужно воспользоваться формулой площади прямоугольника:

S = a * b.

Сторона a совпадает с диагональю основания параллелепипеда.

Длину диагонали основания можно найти по теореме Пифагора, поскольку данная диагональ разбивает прямоугольник на 2 прямоугольных треугольника и является в каждом из них гипотенузой.

BD² = AB² + AD². => BD = √(AB² + AD²).

Сторона b равна высоте параллелепипеда (боковому ребру).

Высоту параллелепипеда можно, например, найти по его объёму и площади основания.

У прямоугольного параллелепипеда основание – это прямоугольник, поэтому площадь основания равна произведению его длины и ширины (на рисунке это AB и AD).

BB1 = V / (AB * AD).

Далее рассмотрим несколько примеров.

**

Пример 1

Стороны основания прямоугольного параллелепипеда равны 12 см и 4 см, а высота равна 5 см.

Нужно найти площадь диагонального сечения.

S (сеч) = √(12² + 4²) * 5 = √140 * 5 = 2√35 * 5 = 10√35 см.

**

Пример 2

Стороны основания и высота прямоугольного параллелепипеда относятся как 1:2:3, а его объём равен 48 см².

Нужно найти площадь диагонального сечения.

1) Сначала найдём, чему равны стороны основания и высота.

V = abc = 48.

Пусть a = x, b = 2x, c = 3x.

x * 2x * 3x = 48.

6x³ = 48.

x³ = 8.

x = 2.

Таким образом, стороны основания равны 2 и 4 см соответственно, а высота равна 6 см.

2) Теперь всё решается так же, как и в 1 примере.

S (сеч) = √(2² + 4²) * 6 = √20 * 6 = 2√5 * 6 = 12√5 см.

Тема: Параллельность прямых и плоскостей

Урок: Задачи на построение сечений в параллелепипеде

Тема урока

В ходе урока все желающие смогут получить представление о теме «Задачи на построение сечений в параллелепипеде».

Повторение свойств параллелепипеда

Рассмотрим параллелепипед АВСDА₁B₁C₁D₁ (рис. 1). Вспомним его свойства.

Рис. 1. Свойства параллелепипеда

1) Противоположные грани (равные параллелограммы) лежат в параллельных плоскостях.

Например, параллелограммы АВСD и А₁B₁C₁D₁ равны (то есть их можно совместить наложением) и лежат в параллельных плоскостях.

2) Длины параллельных ребер равны.

Например, AD = BC = A₁D₁ = B₁C₁ (рис. 2).

Рис. 2. Длины противоположных ребер параллелепипеда равны

3) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Например, диагонали параллелепипеда BD₁ и B₁D пересекаются в одной точке и делятся этой точкой пополам (рис. 3).

Рис. 3.

4) В сечение параллелепипеда может быть треугольник, четырехугольник, пятиугольник, шестиугольник.

Задача на сечение параллелепипеда

Например, рассмотрим решение следующей задачи. Дан параллелепипед АВСDА₁B₁C₁D₁ и точки M, N, K на ребрах AA₁, A₁D₁, A₁B₁соответственно (рис. 4). Постройте сечения параллелепипеда плоскостью MNK. Точки M и N одновременно лежат в плоскости AA₁D₁ и в секущей плоскости. Значит, MN – линия пересечения двух указанных плоскостей. Аналогично получаем MK и KN. То есть, сечением будет треугольник MKN.

Рис. 4.

Задача 1 Построить сечение параллелепипеда

Построить сечение параллелепипеда AD₁ плоскостью А₁В₁М_, где .

Решение (см. рис. 5)

Рис. 5.

1 способ

Соединим точки А₁ и М. Эти точки лежат одновременно в плоскости AA₁D₁ и в секущей плоскости. Значит, А₁М – линия пересечения этих плоскостей.

Если две параллельные плоскости АВВ₁ и DCC₁ рассечены третьей плоскостью (секущей плоскостью), то линии их пересечения параллельны. Поэтому, проведем прямую MN параллельно А₁В₁, . Соединим точки В₁ и N. A₁B₁NM – искомое сечение. Заметим, что A₁B₁NM – параллелограмм. Чтобы найти площадь сечения параллелепипеда, нужно найти площадь полученного параллелограмма.

2 способ

Соединим точки А₁ и М.

Если две параллельные плоскости АDD₁ и BCC₁ рассечены третьей плоскостью (секущей плоскостью), то линии их пересечения параллельны. Поэтому, проведем прямую B₁N параллельно А₁M, . Соединим точки M и N. A₁B₁NM – искомое сечение.

Задача 2 Построить сечение параллелепипеда

Построить сечение параллелепипеда AD₁ плоскостью Р₁Р₂Р_3, где  (рис. 6).

Рис. 6.

Комментарий. В этой и в следующих задачах вид сечения зависит от расположения точек. Например, если бы в задачи 2 расположение точек было бы другим, то и сечение получилось бы иным. И соответственно, площадь сечения параллелепипеда нужно было бы считать по разным формулам.

Решение:

1 способ (рис. 7)

Рис. 7.

Соединим точки Р₁и Р₂ и получим прямую Р₁Р₂ – линию пересечения плоскости АВВ₁ и секущей плоскости.

Соединим точки Р₃и Р₂ и получим прямую Р₃Р₂ – линию пересечения плоскости СВВ₁ и секущей плоскости.

Если две параллельные плоскости АDD₁ и BCC₁ рассечены третьей плоскостью (секущей плоскостью), то линии их пересечения параллельны. Поэтому, проведем прямую Р₁S₁ параллельно Р₃Р₂, .

Если две параллельные плоскости АВВ₁ и DCC₁ рассечены третьей плоскостью (секущей плоскостью), то линии их пересечения параллельны. Поэтому, проведем прямую P₃S₂ параллельно P₁P₂, .

Соединим точки S₁ и S₁. Пятиугольник Р₁Р₂Р₃S₂S₁– искомое сечение.

2 способ (рис. 8)

Рис. 8.

Соединим точки Р₁и Р₂ и получим прямую Р₁Р₂ – линию пересечения плоскости АВВ₁ и секущей плоскости. Продлим прямые Р₁P₂ и АВ до их пересечения в точке Q₁.

Соединим точки Р₃и Р₂ и получим прямую Р₃Р₂ – линию пересечения плоскости СВВ₁ и секущей плоскости. Продлим прямые Р₃P₂ и ВС до их пересечения в точке Q₂.

Точки Q₁ и Q₂лежат в плоскости АВС. Соединим точки Q₁и Q₂. Получаем .

Соединим точки Р₁и S₁, Р₃ и S₂. Пятиугольник Р₁Р₂Р₃S₂S₁– искомое сечение.

Задача 3 Построить сечение параллелепипеда

Изобразите параллелепипед АВСDА₁B₁C₁D₁ и отметьте точку М грани АА₁В₁В. Постройте сечение параллелепипеда, проходящее через точку М параллельно:

а) плоскости основания ABCD

б) плоскости BDD₁.

Решение:

а) Заметим, что секущая плоскость и плоскость АВС пересекаются третьей плоскостью АВВ₁. Значит, линии пересечения параллельны. Поэтому через точку М проведем прямую М₁М₂ параллельно АВ (рис. 9),  , . М₁М₂– это линия пересечения секущей плоскости и грани АВВ₁А₁.

Проведем прямую М₂М₃ параллельно ВС,  .

Проведем прямую М₃М₄ параллельно CD,  .

Соединим точки М₁ и М₄. М₁М₂М₃М₄ – искомое сечение.

 

Рис. 9.

б) Плоскость BDD₁ и секущая плоскость рассекаются третьей плоскостью АВВ₁ по параллельным прямым. Поэтому через точку М проведем прямую N₁N₂ параллельно прямой ВВ₁, .

Проведем прямую N₂N₃ параллельно ВD,  .

Проведем прямую N₁N₄ параллельно B₁D₁,  .

Соединим точки N₃ и N₄. N₁N₂N₃N₄ – искомое сечение.

Рис. 10.

Задача 4 Построить сечение параллелепипеда

Постройте сечение параллелепипеда AD₁ плоскостью ACM_, где . Определите вид полученного сечения.

Решение: (рис. 11)

Параллельные плоскости АВСD и А₁B₁C₁D₁  рассечены плоскостью сечения по параллельным прямым. Значит, через точку М нужно провести прямую NK параллельно АС, .

Соединим точки A и N, K и C. ANKC – искомое сечение. ANKC – трапеция, так как NK || AC.

Рис. 11.

Задача 5 Построить сечение куба

Ребро куба равно а.

1) Постройте сечение куба плоскостью ACN, где N – середина ребра A₁D₁ (рис. 12).

Рис. 12. Построить сечение куба

Решение:

Точки А и С лежат одновременно и в секущей плоскости, и в плоскости АВС. Значит, АС – линия пересечения этих плоскостей.

Параллельные плоскости АВСD и А₁B₁C₁D₁  рассечены плоскостью сечения по параллельным прямым. Значит, через точку N нужно провести прямую NK параллельно АС,  (рис. 13).

Соединим точки A и N, K и C. ANKC – искомое сечение. ANKC – трапеция, так как NK || AC.

Заметим, что NK – средняя линия треугольника A₁D₁C₁.

Рис. 13.

2) Найдите периметр сечения ANKC.

По условию, ребро куба равно а (рис. 14). Значит, диагональ .

Найдем длину отрезка NK: , так как NK – средняя линия треугольника A₁D₁C₁. То есть.

AN = KC, так как треугольники AA₁N и CC₁K равны.

Найдем AN из прямоугольного треугольника AA₁N. По теореме Пифагора  .

Вычислим периметр:

Ответ: .

Рис. 14.

Задача 6

По рисунку (рис. 15) найти точку пересечения прямой MN () и плоскости АВС параллелепипеда AD₁.

Рис. 15.

Решение:

Рассмотрим плоскость АСС₁А₁. В этой плоскости лежит прямая NM и прямая AC. Эти прямые не параллельны. Найдем точку пересечения прямых NM и AC. Обозначим точку пересечения Q (рис. 16).

Точка Q лежит на прямой NM и на прямой АС, а значит и в плоскости АВС. Мы нашли след прямой NM на плоскости АВС. Точка Q – искомая.

Рис. 16. 

Задача 7

Построить сечение параллелепипеда AD₁ плоскостью MNP_, где  (рис. 17).

Рис. 17.

Решение:

Найдем точку пересечения прямой NM и плоскости АВС (см. зад. 6). Обозначим эту точку Q (рис. 18).

Соединим точки Q и Р, так как эти точки лежат одновременно и в плоскости сечения и в плоскости АВС. Получим точки пересечения прямой QР и ребер AD и DC – точки S₁и S₂ соответственно, .

Соединим точки S₁ и N, S₂ и M.

Проведем S₃M параллельно S₁N, .

Проведем S₄N параллельно S₂M, .

Соединим точки S₃ и S₄. S₁S₂MS₃S₄N – искомый шестиугольник.

Рис. 18.

Итоги урока по теме “Сечение параллелепипеда”, “Площадь сечения параллелепипеда”

Итак, мы вспомнили основные свойства параллелепипеда и решили серию типовых задач на построение сечений в параллелепипеде и посчитали периметр и площадь параллелепипеда.

Список рекомендованной литературы по теме “Параллелепипед”, “Сечение параллелепипеда”, “Площадь сечения прямоугольного параллелепипеда”

1. Геометрия. 10-11 класс : учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М. : Мнемозина, 2008. – 288 с. : ил.

2. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.

3. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е издание, стереотип. – М. : Дрофа, 008. – 233 с. :ил.

Рекомендованные ссылки на ресурсы интернет

1. Якласс (Источник)

2. Егэ по математике (Источник)

3. КакПросто (Источник)

4. Myshared.ru (Источник)

Рекомендованное домашнее задание: построить сечение параллелепипеда, посчитать периметр и площадь параллелепипеда

1. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М.: Мнемозина, 2008. – 288 с.: ил.

Задания 13, 14, 15 стр. 50                       

2. Дан параллелепипед АВСDА₁B₁C₁D₁. М и N – середины ребер DC и A₁B₁.

а) Постройте точки пересечения прямых АМ и AN плоскостью грани ВВ₁С₁С.

б) Постройте линию пересечения плоскостей AMN и ВВ₁С₁

3. Постройте сечения параллелепипеда АВСDА₁B₁C₁D₁ плоскостью, проходящей через ВС₁ и середину М ребра DD₁.

Сегодня разберём несложную стереометрическую задачу №4335. На сайте ФИПИ её уровень обозначен, как «повышенный», однако, её решение доступно даже слабым ученикам, помнящим геометрию из средних классов.

Как всегда, напомню, поскольку Дзен плохо поддерживает формулы – я использую скриншоты из редактора.

В дальнейшем для подписчиков планируется возможность получения решений в “вордовском” .DOCX формате со стандартными формулами и рисунками.

Пока – кому требуется, делайте запросы в комментариях – я предоставлю файл. Дальше – что-нибудь придумаем.

Общий список заданий, разобранных на канале, приведён здесь.

Задание

В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB = 7, AD = 3, AA1 = 4. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1:

Рассуждаем.

В условии дан чертёж, из которого видно, что сечение является параллелограммом. Поэтому данный факт доказывать не надо. Но, надо вспомнить следующее правило:

Свойство параллелепипеда: Диагонали параллелепипеда равны.

Поскольку две диагонали параллелепипеда совпадают с диагоналями параллелограмма сечения, отсюда следует, что они равны, а значит, параллелограмм сечения является прямоугольником.

Одна из сторон этого прямоугольника известна, она совпадает с заданной стороной параллелепипеда. Вторую можно найти с помощью теоремы Пифагора. Зная обе стороны – находим площадь.

План решения

• Из теоремы Пифагора найдём длину боковых сторон прямоугольного сечения.
• Зная обе длины сторон прямоугольного сечения, найдём его площадь.

Решение

Замечание

Если бы в условии не было бы чертежа, то дополнительно надо было бы ещё доказать, что сечение проходит через точку D1. Для этого надо вспомнить свойство точки, лежащей на прямой, которая принадлежит плоскости:

Точка лежит в плоскости, если она принадлежит прямой, лежащей в плоскости.

Диагонали параллелепипеда совпадают с диагоналями сечения. Все их точки, включая середину диагоналей, лежат в плоскости сечения. Значит и вторая диагональ, в которую входит и точка D1, также принадлежит плоскости сечения.

Сечение параллелепипеда: как рассчитать его площадь

Масса задач составлена на основе свойств многогранников. Грани объёмных фигур, как и конкретные точки на них, лежат в разных плоскостях. Если одну из таких плоскостей под определённым углом провести сквозь параллелепипед, то часть плоскости, лежащая в пределах многогранника и разделяющая его на части, будет его сечением.

Вам понадобится

• – линейка
• – карандаш

Инструкция

Постройте параллелепипед. Помните, что его основание и каждая из граней должны представлять собой параллелограмм. Это означает, что вам надо построить многогранник так, чтобы все противоположные рёбра параллельны. Если в условии сказано построить сечение прямоугольного параллелепипеда, то его грани сделайте прямоугольными. У прямой параллелепипед прямоугольные только 4 боковые грани. Если боковые грани параллелепипеда не перпендикулярны основанию, то такой многогранник называют наклонным. Если вы хотите построить сечение куба, изначально начертите прямоугольный параллелепипед с равными размерами. Тогда все шесть его граней будут представлять собой квадраты. Назовите все вершины для удобства обозначения.

Обозначьте две точки, которые будут принадлежать плоскости сечения. Иногда их положение указано в задаче: расстояние от ближайшей вершины, конец отрезка, проведённого по определенным условиям. Теперь проведите прямую через точки, лежащие в одной плоскости.

Найдите прямые на пересечении секущей плоскости с гранями параллелепипеда. Для выполнения этого шага найдите точки, в которых прямая, лежащая в плоскости сечения параллелепипеда, пересекается с прямой линией, принадлежащей грани параллелепипеда. Эти прямые должны находиться в одной плоскости.

Достройте сечение параллелепипеда. При этом помните, что ее плоскость должна пересекать параллельные грани параллелепипеда по параллельным прямым.

Стройте секущую плоскость в соответствии с исходными данными в задаче. Существует несколько возможностей построения плоскости сечения, проходящей:
– перпендикулярно заданной прямой линии через заданную точку;
– перпендикулярно заданной плоскости через заданную прямую;
– параллельно двум скрещивающимся прямым через заданную точку;
– параллельно другой заданной прямой через другую заданную прямую;
– параллельно заданной плоскости через заданную точку.
По таким исходным данным стройте сечение по принципу, описанному выше.

Видео по теме

Обратите внимание

Чтобы построить сечение параллелепипеда, нужно определить точки пересечения плоскости сечения с ребрами параллелепипеда, а затем соединить данные точки отрезками. Учтите, что соединять только те точки, которые лежат в плоскости одной грани. Параллельные грани параллелепипеда пересекайте секущей плоскостью по параллельным отрезкам. Если в плоскости грани только одна точка принадлежит плоскости сечения, постройте дополнительную такую точку. Для этого найдите точки пересечения построенных прямых с теми прямыми, которые лежат в нужных гранях.

Полезный совет

Параллелепипед имеет 6 граней. В его сечениях могут получиться треугольники, четырёхугольники, пятиугольники и фигуры с шестью углами. Плоскость, в том числе и секущая, определяется:
– тремя точками;
– прямой линией и одной точкой;
– двумя линиями, параллельными друг другу;
– двумя прямыми, пересекающимися между собой.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?