Как найти площадь сегмента окружности формула - Сайт, где вы сможете решить свои вопросы

Площадь сегмента круга

Главная
/
Математика
/
Геометрия
/
Площадь сегмента круга

Чтобы посчитать площадь сегмента круга воспользуйтесь нашим онлайн калькулятором:

Онлайн калькулятор

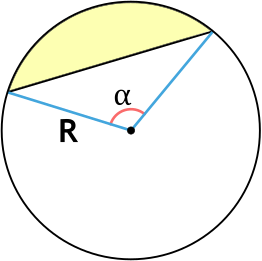
По углу и радиусу

Угол α =
Радиус r =

Площадь сегмента круга

S_ск =

Округление ответа: Округление числа π:

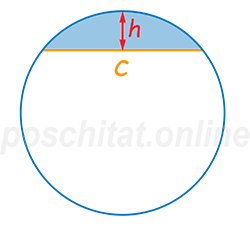
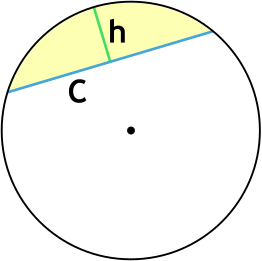
По длине хорды и высоте сегмента

Хорда c =
Высота сегмента h =

Площадь сегмента круга

S_ск =

Округление ответа:

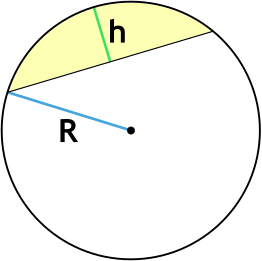
По высоте и радиусу (или диаметру)

=
Высота сегмента h =

Площадь сегмента круга

S_ск =

Округление ответа:

Просто введите данные и получите ответ.

Теория

Площадь сегмента окружности через угол и радиус

Чему равна площадь сегмента окружности S_ск, если её радиус r, а угол сегмента α ?

Формула

В градусах:

S_ск = r²2 ⋅ (π ⋅ α180° – sin α)

В радианах:

S_ск = r²2 ⋅ (α – sin α)

Пример

К примеру, посчитаем площадь сегмента круга, имеющего радиус r = 2 см, а угол сегмента ∠α = 45°:

S_ск = 2²2 ⋅ (3.14 ⋅ 45180 – sin 45) = 2 ⋅ (0.785 – 0.707) = 0.156 см²

Площадь сегмента окружности через хорду и высоту сегмента

Чему равна площадь сегмента окружности S_ск, если длина хорды c, а высота сегмента h ?

Чтобы посчитать площадь сегмента, нам для начала потребуется вычислить радиус окружности r и угол сегмента α. А затем воспользоваться формулой площади сегмента из предыдущего параграфа.

Формула

Радиус круга:

r = c² + 4h²8h

Угол сегмента:

∠α = 2 ⋅ arcsinc2r

Пример

К примеру, посчитаем площадь сегмента круга, имеющего высоту h = 2 см и длину хорды c = 5 см:

r = 5² + 4⋅2²8⋅2 = 25 + 1616 = 2.5625 см∠α = 2 ⋅ arcsin52 ⋅ 2.5625 = 2 ⋅ arcsin 0.9756 ≈ 2.7 radS_ск = 2.5625²2 ⋅ (2.7 – sin 2.7) = 3.2832 ⋅ (2.7 – 0,427) = 7.46 см²

Площадь сегмента окружности через высоту и радиус (или диаметр)

Чему равна площадь сегмента окружности S_ск, если его высота h, а радиус r ?

Если нам известен не радиус, а диаметр, то делим его на 2 и получаем радиус (r = d ÷ 2).

Далее нам остаётся определить угол сегмента α. А затем воспользоваться формулой площади сегмента, описанной выше.

Формула

Угол сегмента:

∠α = 2 ⋅ arccosr – hr

Пример

К примеру, посчитаем площадь сегмента круга, имеющего высоту h = 1 см, а диаметр окружности d = 4 см:

r = 4 ÷ 2 = 2 см

∠α = 2 ⋅ arccos2 – 12 = 2 ⋅ arccos 0.5 = 2.094 radS_ск = 2²2 ⋅ (2.094 – sin 2.094) = 2 ⋅ (2.094 – 0.866) = 2.456 см²

См. также

Источник

Определение сегмента круга

Сегмент — это геометрическая фигура, которая получается путем отсечение части круга хордой.

Онлайн-калькулятор площади сегмента круга

Находится эта фигура между хордой и дугой круга.

Хорда

Это отрезок, лежащий внутри круга и соединяющий две произвольно выбранные точки на нем.

При отсечении части круга хордой можно рассмотреть две фигуры: это наш сегмент и равнобедренный треугольник, боковые стороны которого – радиусы круга.

Площадь сегмента можно найти как разность площадей сектора круга и этого равнобедренного треугольника.

Площадь сегмента можно найти несколькими способами. Остановимся на них более подробно.

Формула площади сегмента круга через радиус и длину дуги круга, высоту и основание треугольника

S=12⋅R⋅s−12⋅h⋅aS=frac{1}{2}cdot Rcdot s-frac{1}{2}cdot hcdot a

RR — радиус круга;
ss — длина дуги;
hh — высота равнобедренного треугольника;
aa — длина основания этого треугольника.

Пример

Дан круг, его радиус, численно равный 5 (см.), высота, которая проведена к основанию треугольника, равная 2 (см.), длина дуги 10 (см.). Найти площадь сегмента круга.

Решение

R=5R=5
h=2h=2
s=10s=10

Для вычисления площади нам не хватает только основания треугольника. Найдем его по формуле:

a=2⋅h⋅(2⋅R−h)=2⋅2⋅(2⋅5−2)=8a=2cdotsqrt{hcdot(2cdot R-h)}=2cdotsqrt{2cdot(2cdot 5-2)}=8

Теперь можно вычислить площадь сегмента:

S=12⋅R⋅s−12⋅h⋅a=12⋅5⋅10−12⋅2⋅8=17S=frac{1}{2}cdot Rcdot s-frac{1}{2}cdot hcdot a=frac{1}{2}cdot 5cdot 10-frac{1}{2}cdot 2cdot 8=17 (см. кв.)

Ответ: 17 см. кв.

Формула площади сегмента круга по радиусу круга и центральном углу

S=R22⋅(α−sin⁡(α))S=frac{R^2}{2}cdot(alpha-sin(alpha))

RR — радиус круга;
αalpha — центральный угол между двумя радиусами, стягивающий хорду, измеряющийся в радианах.

Пример

Найти площадь сегмента круга, если радиус круга равен 7 (см.), а центральный угол 30 градусов.

Решение

R=7R=7
α=30∘alpha=30^{circ}

Переведем сначала угол в градусах в радианы. Поскольку πpi радиан равен 180 градусов, то:
30∘=30∘⋅π180∘=π630^{circ}=30^{circ}cdotfrac{pi}{180^{circ}}=frac{pi}{6} радиан. Тогда площадь сегмента:

S=R22⋅(α−sin⁡(α))=492⋅(π6−sin⁡(π6))≈0.57S=frac{R^2}{2}cdot(alpha-sin(alpha))=frac{49}{2}cdotBig(frac{pi}{6}-sinBig(frac{pi}{6}Big)Big)approx0.57 (см. кв.)

Ответ: 0.57 см. кв.

Не знаете, как выполнить работу с нахождением площади сегмента круга? Наши эксперты помогут вам решить контрольную по геометрии онлайн!

Тест по теме «Площадь сегмента круга»

Источник

У этого термина существуют и другие значения, см. Сегмент.

Сегмент круга закрашен зелёным цветом

Сегме́нт кру́га, кругово́й сегмент — часть круга, ограниченная дугой окружности и её хордой или секущей.

Соотношения[править | править код]

Пусть — радиус круга, — длина хорды сегмента, — длина дуги сегмента, — высота сегмента, также называемая стрелкой сегмента, theta — угол дуги сегмента выраженный в радианах. Размер сегмента круга однозначно задаётся любой парой этих величин и любая величина выражается через любую другую пару. Тогда:

${displaystyle R={frac {s}{theta }}={frac {h}{1-cos {frac {theta }{2}}}}={frac {d}{cos {tfrac {theta }{2}}}}={frac {c}{2sin {tfrac {theta }{2}}}}=h+d={frac {c^{2}+4h^{2}}{8h}}={frac {1}{2}}{sqrt {4d^{2}+c^{2}}};}$

${displaystyle s=theta cdot R=2Rarccos left(1-{tfrac {h}{R}}right)=2Rarccos {tfrac {d}{R}}=2Rarcsin {frac {c}{2R}}=}$

${displaystyle ={frac {theta }{h}}}{1-cos {frac {theta }{2}}={frac {theta d}{cos {tfrac {theta }{2}}}}={frac {theta c}{2sin {tfrac {theta }{2}}}}=}$

${displaystyle =2(h+d)arccos {tfrac {d}{h+d}}={frac {c^{2}+4h^{2}}{4h}}}arcsin {{tfrac {4hc}{c^{2}+4h^{2}}}=}$

${displaystyle ={sqrt {4d^{2}+c^{2}}}}arcsin {{frac {c}{sqrt {4d^{2}+c^{2}}}};}$

${displaystyle c=2Rsin {tfrac {theta }{2}}=R{sqrt {2-2cos theta }}=2{sqrt {h(2R-h)}};}$

${displaystyle h=R(1-cos {tfrac {theta }{2}})=R-{sqrt {R^{2}-{tfrac {c^{2}}{4}}}};}$

${displaystyle theta =2arccos {frac {d}{R}}={frac {s}{R}}=2arccos {frac {R-h}{R}}=2arcsin {frac {c}{2R}}.}$

Площадь кругового сегмента вычисляется по формуле:

${displaystyle S={frac {1}{2}}R^{2}(theta -sin theta )={frac {1}{2}}R^{2}left({frac {s}{R}}-sin {tfrac {s}{R}}right).}$

См. также[править | править код]

	В Викисловаре есть статья «сегмент»

Сектор круга
Шаровой сегмент
Шаровой слой
Коническое сечение
Дуга окружности
Разрез

Это статья-заготовка по математике. Помогите Википедии, дополнив эту статью, как и любую другую.

В статье не хватает ссылок на источники (см. рекомендации по поиску).

Информация должна быть проверяема, иначе она может быть удалена. Вы можете отредактировать статью, добавив ссылки на авторитетные источники в виде сносок. (3 марта 2023)

Источник

В данной публикации мы рассмотрим определение сегмента круга и формулы, с помощью которых можно вычислить его площадь (через радиус и центральный угол кругового сектора). Также разберем примеры решения задач для демонстрации практического применения формул.

Определение сегмента круга
Формулы нахождения площади кругового сегмента
- Через радиус и центральный угол в градусах
- Через радиус и угол сектора в радианах
Примеры задачи

Определение сегмента круга

Сегмент круга – это часть круга, которая ограничена дугой окружности и ее хордой.

Хорда – это часть прямой (секущей), которая пересекает круг. Концы хорды соединяются с центром круга, в результате чего образуется равнобедренный треугольник, боковые стороны которого являются радиусом окружности. Если к этом треугольнику добавить сегмент, получится сектор.

На рисунке выше:

сегмент круга закрашен зеленым цветом;
отрезок AB – это хорда;
часть окружности между точками AB – дуга окружности;
R – радиус круга;
α – угол сектора.

Формулы нахождения площади кругового сегмента

Через радиус и центральный угол в градусах

α° – угол в градусах.

Примечание: в расчетах используется значение π, приблизительное равное числу 3,14.

Через радиус и угол сектора в радианах

α_рад – угол в радианах.

Примеры задачи

Задание 1
Найдите площадь сегмента круга, если его радиус равен 8 см, а центральный угол сектора, стягивающего сегмент, составляет 45 градусов.

Решение
Воспользуемся первой формулой, подставив в нее известные значения:

Задание 2
Площадь кругового сегмента составляет 24 см², а центральный угол сектора круга, частью которого является сегмент, равняется 1 радиану. Найдите радиус круга.

Решение
В данном случае мы можем получить радиус из формулы, в которой задействован угол в радианах:

Источник

Чтобы рассчитать площадь сегмента круга необходимо знать угол сегмента и радиус круга. Введите эти данные в калькулятор и получите результат в режиме онлайн. Кроме этой формулы мы предлагаем еще две, которые помогут найти площадь сегмента круга через радиус и высоту сектора или высоту сектора и хорду.

Сегмент круга – часть круга, ограниченная дугой окружности и её хордой или секущей.

Содержание:

калькулятор площади сегмента круга
формула площади сегмента круга через радиус и угол
формула площади сегмента круга через радиус и высоту
формула площади сегмента круга через высоту и хорду
пример задачи

Формула площади сегмента круга через радиус и угол

{S = dfrac{R^2}{2}(dfrac{pi cdot alpha °}{180°} – sin alpha)}
{S = dfrac{R^2}{2}(alpha – sin alpha)}

R – радиус сегмента круга

α° – угол сегмента круга (если угол в градусах)

α – угол сегмента круга (если угол в радианах)

Формула площади сегмента круга через радиус и высоту

{S = dfrac{R^2}{2}(2 cdot arccos({dfrac{R-h}{R}}) – sin ({2 cdot arccos({dfrac{R-h}{R}})}))}

R – внешний радиус кольца

h – высота сектора кольца

Формула площади сегмента круга через высоту и хорду

{S = dfrac{ Big( dfrac{C^2+4h^2}{8h} Big) ^2}{2}(2 cdot arcsin{dfrac{C}{2R}} – sin (2 cdot arcsin{dfrac{C}{2R}}))}

h – высота сектора кольца

C – хорда

Пример задачи на нахождение площади кольца

Задача 1

Найдите площадь сегмента круга радиуса 4 см, если соответствующий ему центральный угол равен 30 градусов.

Решение

Для решения используем первую формулу с градусной мерой угла.

S = dfrac{R^2}{2}(dfrac{pi cdot alpha °}{180°} – sin alpha) = dfrac{4^2}{2}(dfrac{pi cdot 30 °}{180°} – sin 30) = dfrac{16}{2}(dfrac{pi}{6} – dfrac{1}{2}) = 8(dfrac{pi}{6} – dfrac{1}{2}) = dfrac{8pi}{6} – dfrac{8}{2} = dfrac{4pi}{3} – 4 : см^2 approx 0.18879 : см^2

Ответ: dfrac{4pi}{3} – 4 : см^2 approx 0.18879 : см^2

Убедимся в правильности решения с помощью калькулятора .

Источник

Площадь сегмента круга

Онлайн калькулятор

По углу и радиусу

По длине хорды и высоте сегмента

По высоте и радиусу (или диаметру)

Теория

Площадь сегмента окружности через угол и радиус

Формула

Пример

Площадь сегмента окружности через хорду и высоту сегмента

Формула

Пример

Площадь сегмента окружности через высоту и радиус (или диаметр)

Формула

Пример

См. также

Онлайн-калькулятор площади сегмента круга

Формула площади сегмента круга через радиус и длину дуги круга, высоту и основание треугольника

Формула площади сегмента круга по радиусу круга и центральном углу

Тест по теме «Площадь сегмента круга»

Соотношения[править | править код]

См. также[править | править код]

Определение сегмента круга

Формулы нахождения площади кругового сегмента

Через радиус и центральный угол в градусах

Через радиус и угол сектора в радианах

Примеры задачи

Содержание:

Формула площади сегмента круга через радиус и угол

Формула площади сегмента круга через радиус и высоту

Формула площади сегмента круга через высоту и хорду

Пример задачи на нахождение площади кольца

Вам также может понравиться

Как можно найти работа прямо хазайн

Как найти кто участковый в ростове

Как найти лиз гта 5

Добавить комментарий Отменить ответ