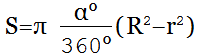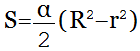Как найти площадь сектора кольца

Как найти площадь сектора кольца

Как рассчитать площадь сектора кольца

На данной странице калькулятор поможет рассчитать площадь сектора кольца онлайн. Для расчета задайте радиус и угол сектора кольца.

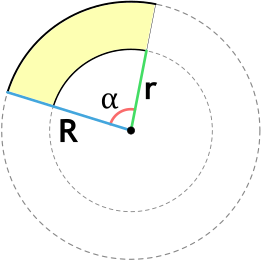
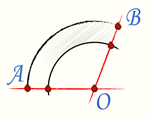
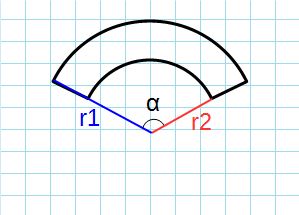
Сектор кольца – это часть круга, ограниченная дугами разных радиусов, проведенных из одной точки, и двумя радиусами, проведенными к концам большей дуги.

Через угол и радиус

Площадь сектора кольца

Формула для нахождения площади сектора кольца:

 — в градусах;

 — в радианах;

π – константа равная (3.14); α – угол сегмента круга; r1 – радиус внешней окружности; r2 – радиус внутренней окружности.

Источник

На этой странице с помощью калькулятора и формулы можно найти площадь сектора кольца через радиусы и угол сектора кольца.

Сектор кольца — это часть круга, ограниченная дугами разных радиусов, проведенных из одной точки – центра, и двумя радиусами, проведенными к концам дуги большего радиуса..

Содержание:
  1. калькулятор площади сектора кольца
  2. формула площади сектора кольца для угла в градусах
  3. формула площади сектора кольца для угла в радианах
  4. пример задачи

Формула площади сектора кольца для угла в градусах

Площадь сектора кольца для угла в градусах

{S = pi dfrac{alpha °}{360°}(R^2 – r^2)}

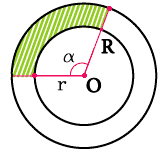
R – внешний радиус кольца

r – внутренний радиус кольца

α – угол сектора кольца (в градусах)

Формула площади сектора кольца для угла в радианах

Площадь сектора кольца для угла в радианах

{S = dfrac{alpha}{2}(R^2 – r^2)}

R – внешний радиус кольца

r – внутренний радиус кольца

α – угол сектора кольца (в радианах)

Пример задачи на нахождение площади сектора кольца

Задача 1

Найдите площадь сектора кольца, если внешний радиус кольца 5 см, внутренний радиус 3см, а угол сектора 45 градусов.

Решение

Подставим значения из условия в первую формулу и произведем расчет.

S = pi dfrac{alpha °}{360°}(R^2 – r^2) = pi dfrac{45 °}{360°}(5^2 – 3^2) = pi dfrac{1}{8}(25 – 9) = pi dfrac{1}{8} cdot 16 = 2pi : см^2 approx 6.28319 : см^2

Ответ: 2pi : см^2 approx 6.28319 : см^2

Проверить правильность решения задачи нам поможет калькулятор .

Источник

Площадь сектора кольца, формула

Площадь сектора кольца
Сектор кольца — это часть круга, окружности ограниченная дугами разных радиусов и двумя линиями радиусами, проведенными к концам дуги большего радиуса.

Площадь сектора кольца вычисляется как разность площадей большего и меньшего секторов круга

Площадь сектора кольца если угол в градусах

Площадь сектора кольца если угол в градусах, вычисляется как произведение числа π на отношение угла сектора к углу полной окружности 360° и на разность квадратов большего и меньшего радиусов.

[ S = pi frac{α°}{360°} (R^2 – r^2) ]

Вычислить, найти площадь сектора кольца если угол в градусах по формуле (1)

Площадь сектора кольца если угол в радианах

Площадь сектора кольца если угол в радианах, вычисляется как произведение половины угла сектора на разность квадратов большего и меньшего радиусов.

[ S = frac{α}{2} (R^2 – r^2) ]

Вычислить найти площадь сектора кольца если угол в радианах по формуле (2)

Площадь сектора кольца

 стр. 311
Источник

Сектор кругового кольца – это плоская фигура, которая представляет собой часть плоскости между дугами двух окружностей с общим центром и разным радиусами, ограниченных двумя радиальными линиями, которые проведены к концам дуги с большим радиусом.

Формула площади сектора кольца, выраженная через внешний и внутренний радиусы

сектор кольца
Пусть дана окружность радиуса R и окружности радиуса r. Причем R>r. Совместим центры этих окружностей. Возьмем на окружности с большим радиусом две произвольные точки. Проведем к ним радиусы, которые образуют угол α. Эти радиусы отсекут от окружностей некоторые дуги. Фигура, заключенная между этими дугами окружностей и радиусами, проведенными к концам этих дуг, и будет сектор кольца, у которого R является внешним радиусом, r -внутренним радиусом.
Тогда площадь этой фигуры будет равна разницы между площадью сектора круга с большим радиусом и площадью сектора круга с меньшим радиусом.
Площадь сектора круга с радиусом r выражается формулой:

S={1/2}lr

где l–длина дуги равная {{pi}/{180}^o }{alpha}
Подставим выражение длины дуги в формулу площади сектора. Получим:
S={1/2}* r {{{pi}r}/{180}^o} {alpha}={{{pi}r^2}/{360}^o }{alpha}
Площадь круга с радиусом R выражается формулой: S={1/2}LR
где L–длина дуги равная {{pi}/{180}^o }{alpha}
Подставим выражение длины дуги в формулу площади сектора. Получим:
S={1/2}r {{{pi}R}/{180}^o} {alpha}={{{pi}R^2}/{360}^o}{alpha}
Тогда площадь кольца будет равна:
S={{{pi}r^2}/{360}^o} {alpha}-{{{pi}R^2}/{360}^o} {alpha}={{pi}(R^2-r^2)}/{360}^o {alpha}
Таким образом, площадь сектора кольца равна произведению площади единичного сектора кольца, то есть сектору, соответствующему центральному углу с мерой равной единице на меру центрального угла, соответствующего данному сектору.
Формула имеет вид: S={{{pi}(R^2-r^2)}/{360}^o}{alpha}

Иконка карандаша 24x24Пример расчета площади сектора кольца, если известны его радиусы.
Найдите площадь сектора кольца, образованного углом 30° , если его внешний радиус равен 14, а внутренний – 8.
Площадь кольца вычисляется по формуле:
S={{{pi}(R^2-r^2)}/{360}^o }{alpha}
Подставив значения из условия задачи, имеем:
S={{{pi}({14}^2-8^2)}/{360}^o} *{30}^o={{{pi}(196-64)}/{360}^o} *{30}^o={{{pi}141}/{360}^o} *{30}^o=11,75{pi}

Источник

Сектор кольца — это часть круга, которая ограничена внутренней дугой кольца, внешней дугой кольца и двумя внешними радиусами кольца. Площадь сектора кольца вычисляется как разность площадей большего и меньшего секторов круга.

Установить Площадь сектора кольца на мобильный

Площадь сектора кольца (градусы)

Площадь сектора кольца градусы формула Площадь сектора кольца градусы
Угол сектора кольца (градусы) a
Внешний радиус кольца R
Внутренний радиус кольца r
Результат

Площадь сектора кольца (радианы)

Площадь сектора кольца радианы формула Площадь сектора кольца радианы
Угол сектора кольца (радианы) a
Внешний диаметр кольца R
Внутренний диаметр кольца r
Результат

Скачать калькулятор

Рейтинг: 2.3 (Голосов 3)

×

Пожалуйста напишите с чем связна такая низкая оценка:

×

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке

Смотрите также

Площадь фигур Объем фигур Периметр фигур Радиус фигур Единицы измерения площади
Конвертеры Время для пробуждения Теоремы Угол Калькулятор Моей жизни
Источник

Добавить комментарий