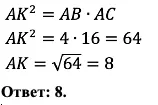Как найти площадь сектора круга егэ - Сайт, где вы сможете решить свои вопросы

было в ЕГЭ

в условии
в решении
в тексте к заданию
в атрибутах

Категория

Атрибут

Всего: 444 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

На клетчатой бумаге с клетками размером 1 см times 1 см

изображен треугольник (см. рис.). Найдите его площадь в квадратных

сантиметрах.

На клетчатой бумаге с клетками размером 1 см times 1 см

изображен треугольник (см. рис.). Найдите его площадь в квадратных

сантиметрах.

На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рис.). Найдите его площадь в квадратных сантиметрах.

На клетчатой бумаге с клетками размером 1 см  times  1 см изображен треугольник (см. рис.). Найдите его площадь в квадратных сантиметрах.

Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

На клетчатой бумаге с клетками размером 1 см times 1 см изображена трапеция (см. рис.). Найдите ее площадь в квадратных сантиметрах.

На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.

Всего: 444 1–20 | 21–40 | 41–60 | 61–80 …

Источник

3 октября 2013

В этом уроке мы разберем еще одну задачу B5 на площади секторов из ЕГЭ по математике, однако будьте очень внимательны: на первый взгляд все считается очень просто. Но в самом конце решения многие ученики допускают очень обидную ошибку. Сейчас вы поймете, о чем идет речь. Итак, задача:

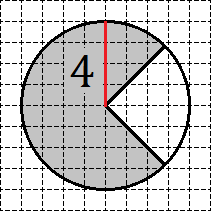
Задача. Найдите площадь S закрашенного сектора, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π.

Как решать такую задачу? В первую очередь, поскольку речь идет о площади сектора, нам нужно знать формулу площади круга:

S = πR²

где R — радиус круга. Следовательно, для решения нам потребуется найти этот самый радиус. В данной задаче все очень просто: проводим вертикальный радиус и считаем клеточки.

Отсюда сразу получаем, что радиус R = 4. Таким образом, площадь круга S равна:

S = π · 4² = 16π

Обратите внимание: нам очень повезло с радиусом. Потому что в настоящих задачах далеко не всегда верхняя точка окружности лежит в узлах координатной сетки. Однако где-то на окружности обязательно найдется точка с целочисленными координатами, которая точно будет лежать в узле сетки. Вот ее и надо использовать для вычисления радиуса. Давайте посмотрим, каким образом.

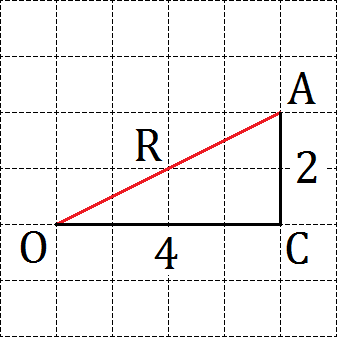
Для этого нам потребуется отдельная сетка. Отметим на ней центр окружности (точку O) и некую гипотетическую точку A, которая должна лежать на нашей окружности. Допустим, это будет выглядеть следующим образом:

Тогда отрезок OA будет радиусом этой окружности. Как его найти? Достроим до прямоугольного треугольника наш отрезок. Если двигаться вдоль линий координатной сетки, мы получим прямоугольный треугольник OAC с прямым углом C. Разумеется, полученная таким образом точка C не будет лежать на окружности — она лежит где-то внутри. Но этого нам и не требуется. Главное, что мы легко можем найти катеты: OC = 4, AC = 2.

Тогда мы можем найти радиус R (он же — отрезок OA) по теореме Пифагора:

R² = 4² + 2² = 16 + 4 = 20

И тогда получилось бы, что вместо 16π площадь всего круга равнялась бы 20π. В остальном решение было бы полностью аналогичным, поэтому возвращаемся к нашей исходной задаче. Мы только что нашли площадь круга, а нам надо найти площадь сектора. Давайте схематично перерисуем круг и разделим его на 8 равных частей, как пиццу (стандартная практика в задачах B5). Затем закрашиваем на получившемся рисунке те сектора, которые на исходном чертеже также были закрашены:

Получаем, что закрашенных кусочков было k = 6, а всего их изначально n = 8. Поскольку все части равные, мы можем найти площадь каждого маленького сектора, разделив общую площадь круга на 8:

S_sec = 16π/8 = 2π

А поскольку в закрашенном секторе таких кусочков k = 6, то искомая площадь будет равна

S = 6 · S_sec = 6 · 2π = 12π

Но в задаче B5 от нас требуется найти не просто площадь сектора, а величину S/π. Поэтому выполняем последний шаг. Подставляем и получаем:

12π : π = 12

Это и есть ответ. Так в чем же главная ошибка учеников, которые решают подобные задачи? Дело в том, что многие начинают считать площадь меньшего из секторов, изображенных на рисунке. Однако этот сектор не закрашен. В результате при правильных по существу расчетах многие ученики получают неправильный ответ. Согласитесь, обидная ошибка?

Поэтому рекомендация следующая: внимательно читайте условие задачи B5! Если требуется найти площадь закрашенного сектора, то именно закрашенный сектор и нужно искать. Даже если на чертеже он занимает большую часть круга. А если требуется найти площадь незакрашенного сектора, то об этом обязательно будет указано в условии. Поэтому прежде чем записывать ответ, еще раз проверьте, что от вас требуется: закрашенный сектор или незакрашенный? И тогда дополнительный балл на ЕГЭ по математике вам гарантирован.:)

Смотрите также:

Задача B5: площадь кольца
Задача B5: площадь сектора
Как сдать ЕГЭ по математике
Метод коэффициентов, часть 1
Задача B5: метод узлов
Сфера, описанная вокруг куба

Источник

Определения

Окружность – это множество всех точек плоскости, равноудалённых от некоторой точки (называемой центром окружности).

Радиус окружности – это отрезок, соединяющий центр окружности и точку на окружности. Иногда радиусом окружности называют длину этого отрезка.

Дуга окружности – это часть окружности, заключённая между двумя точками на окружности.

Круг (радиуса (R,)) – это множество всех точек плоскости, удалённых от некоторой точки на расстояние меньшее или равное (R > 0).

Круговой сектор – это часть круга, ограниченная дугой (называемой дугой сектора) и двумя радиусами, соединяющими концы дуги с центром круга.

Теорема (рис. 1)

Длина окружности радиуса (R) равна (C=2pi R).

Длина дуги окружности радиуса (R) равна (C_{alpha}=2pi Rcdotdfrac{alpha}{360}), где (alpha^circ) – градусная мера этой дуги.

Теорема (рис. 2)

Площадь круга радиуса (R) равна (S=pi R^{,2}).

Площадь кругового сектора круга радиуса (R) равна (S_{alpha}=pi
R^{,2}cdotdfrac{alpha}{360}), где (alpha^circ) – градусная мера дуги сектора.

Доказательство

1) Т.к. градусная мера всей окружности равна (360^circ), то длина дуги в (1^circ) равна (dfrac1{360}) части от всей окружности: [C_{1^circ}=2pi Rcdot dfrac1{360}]

Тогда длина дуги в (alpha^circ) равна (C_{alpha}=2pi
Rcdotdfrac{alpha}{360}).

2) Аналогично.

Источник

Окружность на ЕГЭ и ОГЭ — сложно. Все потому, что эта фигура не похожа на остальные: у неё нет углов и сторон, зато есть совсем другие элементы. В этой статье мы подробно поговорим про элементы окружности, углы, отрезки и прямые, которые с ней связаны, а также обсудим длину окружности и площадь круга. Ну и разберем основные задания ЕГЭ и ОГЭ, конечно же!

В этой статье:

Углы у окружности на ЕГЭ и ОГЭОтрезки и прямые в окружности на ЕГЭ и ОГЭ4 теоремы про окружность в ЕГЭ и ОГЭДлина окружности и площадь кругаЧто нужно иметь в виду для ЕГЭ и ОГЭ

Все об окружности на ЕГЭ и ОГЭ — разбор заданий и задач

Для начала давайте разберёмся, что же такое окружность. Окружность — это замкнутая линия, состоящая из множества точек, которые равноудалены от центра окружности. Основной элемент окружности — это радиус, он соединяет центр с любой точкой на окружности.

Углы у окружности на ЕГЭ и ОГЭ

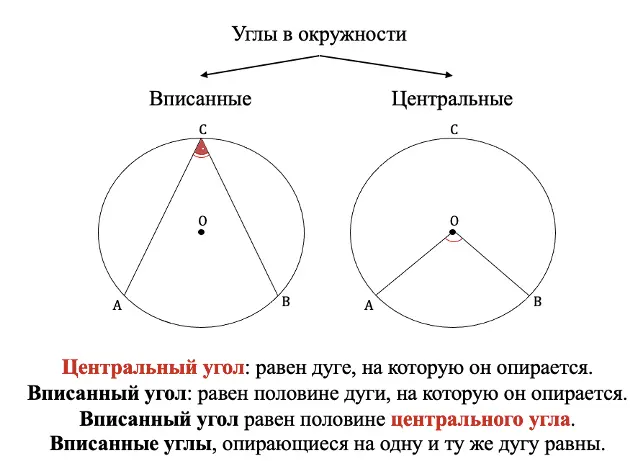
У окружности есть 2 вида углов:

вписанные (их вершина лежит на окружности);
центральные (тут всё понятно из названия, у них вершина в центре окружности).

Расположение и свойства углов в окружности можно увидеть на схеме ниже:

Теория: углы в окружности на ЕГЭ и ОГЭ

Давайте отработаем это на практике:

Задание на углы окружности в ЕГЭ и ОГЭ

Решение

Можно заметить, что угол АСВ — вписанный и опирается на дугу АВ, соответственно, центральный угол АОD, опирающийся на ту же дугу будет в 2 раза больше, то есть 70 градусов. Теперь рассмотрим развёрнутый угол ВОD, он состоит из углов АОВ и АОD. Градусная мера развёрнутого угла 180 градусов, следовательно искомый угол АОD будет равен 180 – 70 = 110 градусов.

Отрезки и прямые в окружности на ЕГЭ и ОГЭ

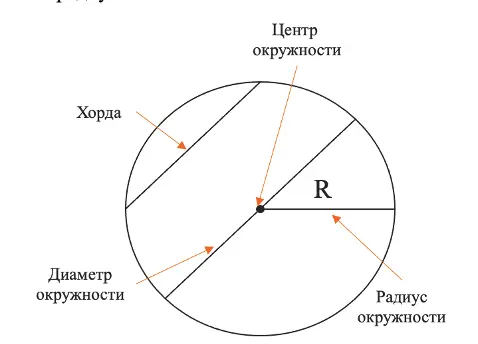
Теперь рассмотрим отрезки и прямые в окружности. Приготовьтесь, их будет много!

Есть хорда — это отрезок, который соединяет 2 любые точки на окружности. Если хорда пройдёт через центр окружности, то она превратится в диаметр. Кстати, если внимательно посмотреть, то можно увидеть, что диаметр — это 2 радиуса!

Хорда, диаметр, радиус и центр окружности на схеме

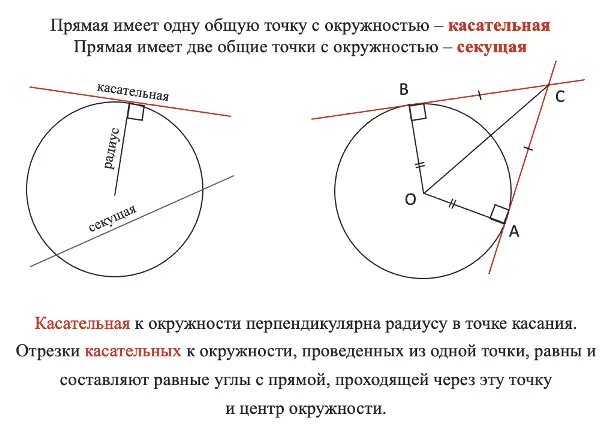
Теперь продлим хорду в обе стороны за пределы окружности, получим прямую, которая переСЕКает нашу окружность, отсюда и её название — секущая. Можно заметить, что секущая имеет 2 общих точки пересечения с окружностью. А ещё мы можем провести прямую так, чтобы она имела с окружностью только 1 точку пересечения, то есть касалась её, такая прямая будет называться касательная.

Подробнее со свойствами касательной и секущей можно ознакомиться на рисунке:

Свойства касательной и секущей в окружности на схеме

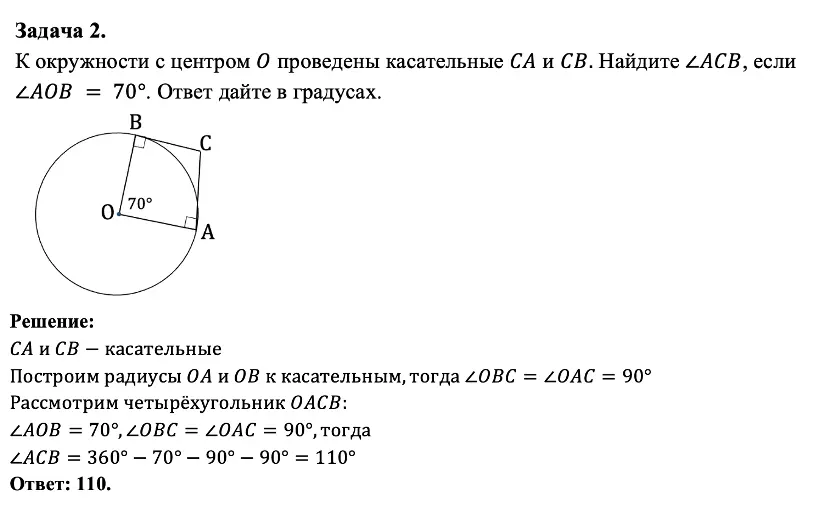
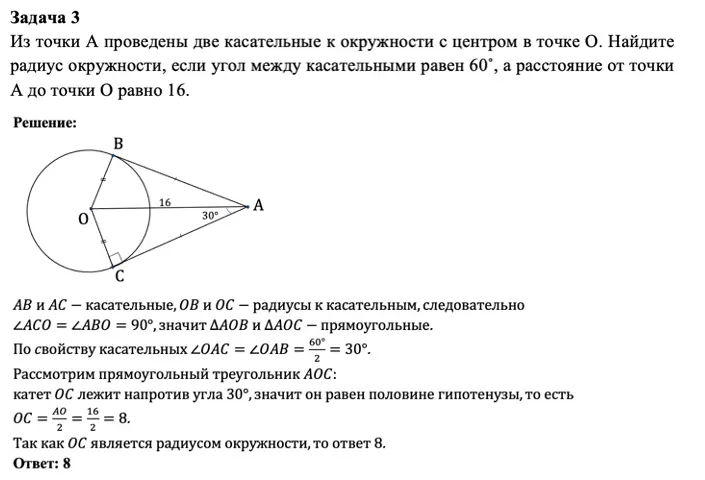
Рассмотрим на примерах заданий про окружность в ЕГЭ и ОГЭ:

Первый пример задания на касательную в окружности на ЕГЭ и ОГЭ

Второй пример задания на касательную в окружности на ЕГЭ и ОГЭ

4 теоремы про окружность в ЕГЭ и ОГЭ

Теперь я предлагаю ознакомиться с теоремами, которые появляются в комбинациях различных прямых и отрезков в окружности.

Теорема № 1: теория и задания из ЕГЭ и ОГЭ

Первая теорема про хорду и касательную звучит так:

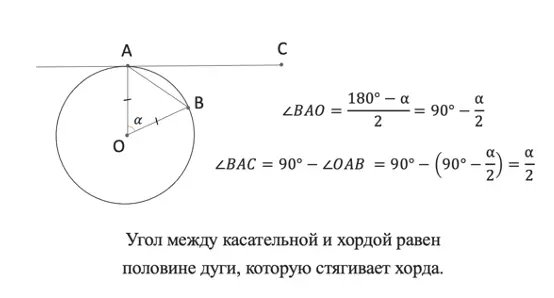
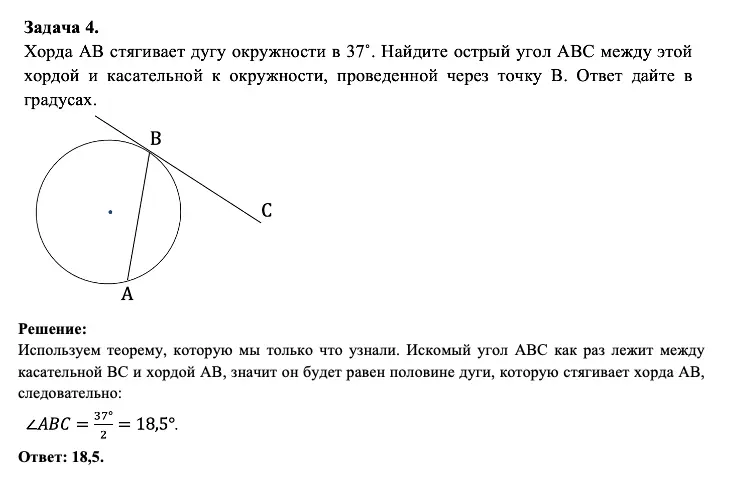
Угол между касательной и хордой равен половине дуге, которую стягивает хорда.

Подробнее с выведением вы можете ознакомиться на рисунке:

Вот так выводится теорема про хорду и касательную

Однако хочу обратить ваше внимание, что если вы просто запомните формулировку, то многие задачи на окружность в ЕГЭ и ОГЭ покажутся вам супер-простыми и будут решаться в 1 действие. Давайте в этом убедимся:

Пример решения задачи на окружность в ЕГЭ и ОГЭ с использованием теоремы про хорду и касательную

Вот так просто и быстро в 1 действие мы справились с задачей. Правда здорово?!

Теорема № 2: теория и задания из ЕГЭ и ОГЭ

А теперь давайте посмотрим на одну из моих самых любимых теорем. А любимая она, потому что без неё некоторые задачи кажутся практически нерешаемыми, а с ней их можно решить быстро и просто! Звучит она так:

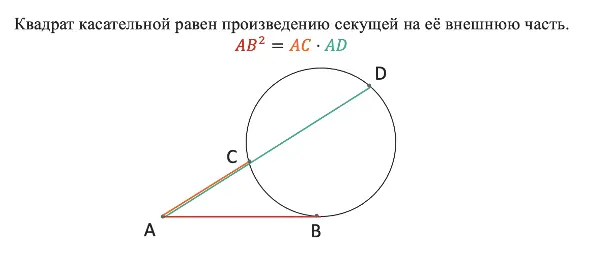
Квадрат касательной равен произведению секущей на её внешнюю часть.
Я советую запоминать именно словесную формулировку, так как чертежи и буквы на них могут быть разными, и есть риск всё перепутать.

Наглядно познакомиться с теоремой можно на рисунке ниже:

Теорема: квадрат касательной равен произведению секущей на её внешнюю часть

И конечно же давайте отработаем на практике!

Пример задания на теорему № 2

Если бы мы не знали ту теорему, которую только что прошли, то было бы много версий, как можно решить задачу. Кто-то начал бы строить радиус к касательной и рассматривать треугольники, а кто-то просто не стал бы решать, однако у нас есть формула: давайте её используем!

Решение:

Вот так просто решается это задание!

Теорема № 3: теория и задания из ЕГЭ и ОГЭ

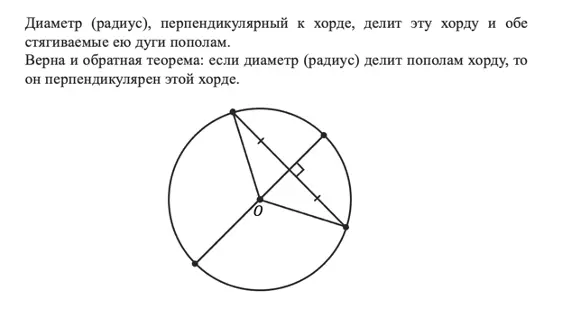
Если вы ещё не устали от теорем, то давайте познакомимся с ещё одной, которая связывает хорду с диаметром (радиусом).

Эта теорема интересна тем, что работает в обе стороны:

Вот так хорду можно связать с диаметром (радиусом)

Конечно же я не могу оставить вас без тренировки, поэтому посмотрим на следующую задачу:

Задание на нашу теорему и его решение

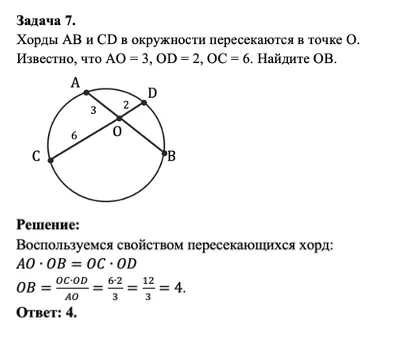
Теорема № 4: пересекающиеся хорды

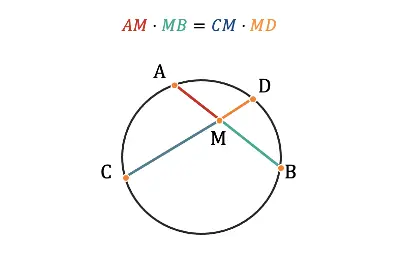
Последнее, с чем я вас познакомлю в контексте прямых и отрезков в окружности будет свойство пересекающихся хорд:

Произведения отрезков пересекающихся хорд равны.

Свойство пересекающихся хорд на рисунке

Для наглядности отрезки выделены разными цветами, так вам будет проще запомнить свойство.

А теперь отработаем его на практике:

Задание на свойство пересекающихся хорд и его решение

Длина окружности и площадь круга

Вот мы и подошли с вами к самому интересному, формулам длины окружности и площади круга, давайте их запишем:

Формулы длины окружности и площади круга

Эти формулы очень походы, в них есть двойка, число Pi и радиус, однако можно заметить, что у формулы длины окружности двойка слева, а у площади круга справа в степени.

Так как же их не путать? Очень просто: запомните, что вторая степень (или квадрат) должна быть у площади, значит двойка слева будет у длины.

Давайте это закрепим:

Задание на длину окружности и площадь круга в ЕГЭ и ОГЭ

Вот так просто и быстро мы закрепили сразу обе формулы.

Как находить площадь и длину дуги сектора круга: задачи

А теперь перейдём к самому интересному — нахождению площади и длины дуги сектора круга. Многие ученики думаю, что это сложно, но на самом деле это не так. Я предлагаю записать 2 коротких алгоритма, с помощью которых вы сможете легко найти площадь или длину дуги сектора.

2 алгоритма для поиска площади и длины дуги сектора

И конечно же давайте закрепим эти алгоритмы на практике:

Задача на поиск площади сектора круга в ЕГЭ и ОГЭ

Теперь вы умеете решать задания на поиск площади сектора. Согласитесь, что с алгоритмом всё намного понятнее и проще?

Что нужно иметь в виду для ЕГЭ и ОГЭ

На самом деле это всё, что я хотела вам рассказать в данной статье. Давайте ещё раз повторим, что вы узнали.

Сначала мы познакомились с понятием окружность, потом посмотрели, какие бывают углы в окружности.
Затем увидели множество отрезков и прямых в окружности, записали их свойства, а также несколько теорем с ними.
В завершение мы поговорили про длину окружности, площадь круга, а также поиск площади и длины дуги сектора.

Самое ценное, что всю теорию мы закрепили на реальных заданиях из ОГЭ и ЕГЭ. Конечно, это далеко не всё, что вам может встретиться. Если вы хотите хорошо разбираться в окружности и в других темах, которые встречаются на экзаменах, записывайтесь на наши курсы подготовки к ОГЭ и ЕГЭ. На них мы подробно изучаем всю теорию, решаем много заданий, запоминаем удобные лайфхаки и решаем пробные экзамены, чтобы не стрессовать на реальном. Присоединяйтесь!

Источник

Площадь круга равна произведению числа displaystyle pi на квадрат радиуса:
$displaystyle S=pi R^{2}.$
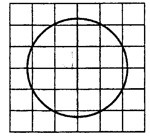
Задача 1. Найдите площадь круга, считая стороны клеток равными 1 (см. рис. 1). В ответе укажите $displaystyle frac{S}{pi }$ .

Рис.1

Решение.
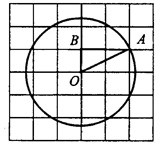
Площадь круга равна произведению числа displaystyle pi на квадрат радиуса. Найдём радиус. Из центра проведём радиус . В треугольнике OAB сторона — гипотенуза, катеты равны 1 и 2 (см. рис. 2).

Рис.2

Найдём гипотенузу по теореме Пифагора. $displaystyle OA=sqrt{1^{2}+2^{2}}=sqrt{5}.$
Площадь круга $displaystyle S=pi (sqrt{5})^{2}=5pi .; frac{S}{pi }=frac{5pi }{pi }=5.$
Ответ: 5.
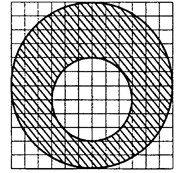
Задача 2. На клетчатой бумаге нарисовано два круга (см. рис. 3). Площадь внутреннего круга равна 3. Найдите площадь заштрихованной фигуры.

Рис.3

Решение.
Радиус внутреннего круга — 3 клетки, его площадь равна $displaystyle pi R^{2}=3$ . Радиус внешнего круга — 6 клеток, то есть , поэтому его площадь равна $displaystyle pi (2R^{2})=3cdot 4=12.$ Площадь заштрихованной фигуры равна разности 12 — 3 = 9.
Ответ: 9.
Площадь сектора с углом displaystyle alpha градусов равна $displaystyle frac{pi R^{2}alpha }{360^{circ}}.$
Задача 3. Найдите площадь сектора с углом 18 градусов и радиусом 4. В ответе укажите $displaystyle frac{S}{pi }$ .
Решение.
Посчитаем площадь сектора по формуле $displaystyle S=frac{pi R^{2}alpha }{360}=frac{pi cdot 4^{2}cdot 18}{360}=0,8pi cdot frac{S}{pi }=0,8.$
Ответ: 0,8.
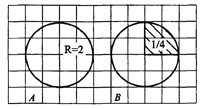
Задача 4. Найдите площадь заштрихованного сектора, считая стороны клеток равными 1 (см. рис. 4). В ответе укажите $displaystyle frac{S}{pi }$ .

Рис.4

Решение.
На рисунке 4A) площадь круга с радиусом = 2 равна $displaystyle pi R^{2}=pi cdot 2^{2}=4pi .$
На рисунке 4В) площадь сектора составляет $displaystyle frac{1}{4}$ от площади круга (если круг разделить на 4 равные части, то одна из них как раз и будет равна заданному сектору), то есть
$displaystyle frac{pi R^{2}}{4}=frac{pi cdot 2^{2}}{4}=pi.$
Можно было решать задачу по-другому. Площадь сектора равна площади круга, делённой на 4.
displaystyle S:4=4pi :4=pi.
Ответ: 1.
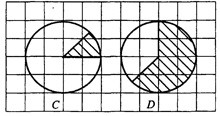
Задача 5. Найдите площадь заштрихованных секторов на рисунках C и D, считая стороны клеток равными 1 (см. рис. 5).

Рис.5

В ответе укажите $displaystyle frac{S}{pi }$ .
Решение. Посчитаем, какая часть круга закрашена. Проведя дополнительные линии (см. рис. 6), видим, что сектор на рисунке 6C) составляет – часть круга, а сектор на рисунке 6D) составляет
$displaystyle frac{5}{8}$ частей круга (круг разделён на 8 равных частей, и закрашено 5 таких частей).
Находим площади секторов на рисунках 6C) и 6D).

Рис.6

1-й способ.
Поделим площадь круга на 8, получим площадь сектора на рисунке 6C), потом умножим эту площадь на 5, получим площадь сектора на рисунке 6D).
$displaystyle S_{C}=4pi :8=0,5pi ;; frac{S}{pi }=0,5;; S_{D}=4pi :8cdot 5=2,5pi ;frac{S}{pi }=2,5.$
Ответ: 0,5 и 2,5.
2-й способ. Найдём площадь $displaystyle frac{1}{8}$ круга.
$displaystyle S_{C}=frac{1}{8}cdot 4pi =0,5pi ;; frac{S}{pi }=0,5;; S_{D}=frac{5}{8}cdot 4pi =2,5pi ;; frac{S}{pi }=2,5.$
Ответ: 0,5 и 2,5.

Источник

Углы у окружности на ЕГЭ и ОГЭ

Решение

Отрезки и прямые в окружности на ЕГЭ и ОГЭ

4 теоремы про окружность в ЕГЭ и ОГЭ

Теорема № 1: теория и задания из ЕГЭ и ОГЭ

Теорема № 2: теория и задания из ЕГЭ и ОГЭ

Теорема № 3: теория и задания из ЕГЭ и ОГЭ

Теорема № 4: пересекающиеся хорды

Длина окружности и площадь круга

Как находить площадь и длину дуги сектора круга: задачи

Что нужно иметь в виду для ЕГЭ и ОГЭ

Вам также может понравиться

Findclosestmatchingmode как исправить

Как составить свой устав

The filename directory name or volume label syntax is incorrect как исправить

Добавить комментарий Отменить ответ