Как рассчитать площадь сектора круга
На данной странице калькулятор поможет рассчитать площадь сектора круга онлайн. Для расчета задайте радиус, длину дуги или угол сектора круга.
Сектор круга – это часть круга, окружности ограниченная дугой и двумя радиусами, проведенными к концам дуги.
Через длину дуги и радиус
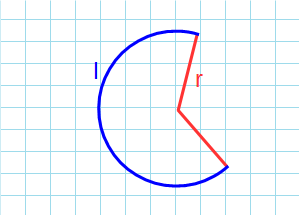
Формула для нахождения площади сектора круга:
l – длина дуги окружности; r – радиус окружности.
Через угол и радиус
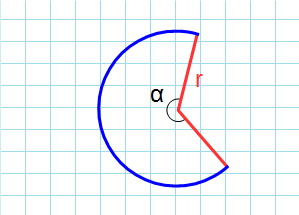
Формула для нахождения площади сектора круга:
— в градусах;
— в радианах;
π – константа равная (3.14); α – угол сектора круга; r – радиус окружности.
Сектор круга ограничивается дугой между двумя точками A и B на окружности и двумя радиусами, проведенными из концов дуги (точек A и B) к центру круга. Два радиуса делят всю площадь круга на 2 сектора, если угол между радиусами будет развернутым (180 градусов), то эти секторы будут между собой равны. Площадь сектора круга – это часть S всей плоской фигуры, ограниченной окружностью с радиусом r.
Площадь круга равна произведению квадрата радиуса на число «пи».
Площадь сектора может быть выражена формулой S = π х r² х α/360. В ином виде при указании угла сектора α не в градусах, а в радианах, S = (α/2) х r². Расчет площади сектора круга можно также осуществить еще по одной формуле через длину секторной дуги.
В разделе представлены сразу три варианта формул онлайнового калькулятора. Работники конструкторских отделов, а также пока еще познающие основы конструирования сложного оборудования, обучающиеся в Вузах студенты, могут воспользоваться любым из них на свой выбор.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Через длину дуги сектора
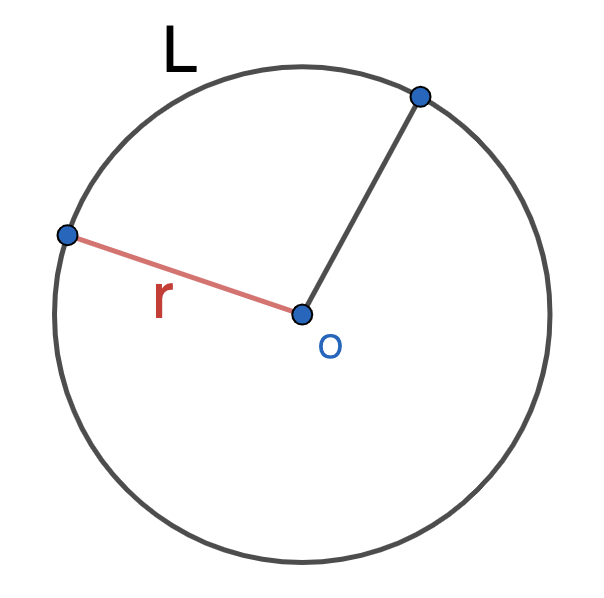
Длина дуги (L)
Радиус (r)
Через угол сектора в градусах
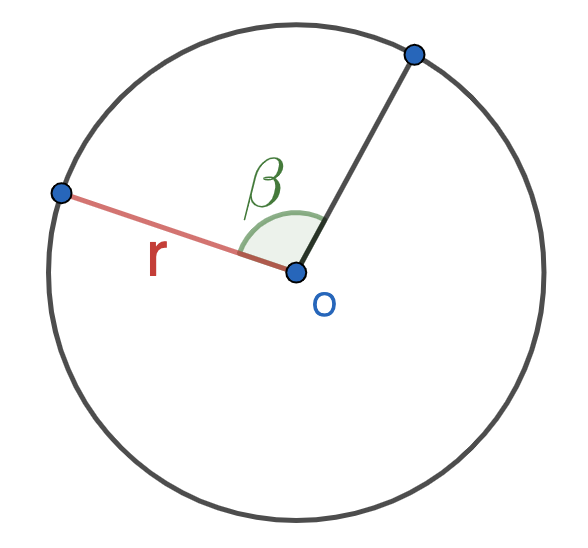
Угол (°)
Радиус (r)
Через угол сектора в радианах
Угол (RAD)
Радиус (r)
Введите в онлайн калькулятор необходимые для вычисления значения и нажмите кнопку Посчитать.
Формулы
(S = frac{1}{2}*L*r)
(S = pi*r^2*frac{beta}{360})
(S = frac{a}{2}*r)
L – длина дуги,
r – радиус круга,
(beta) – угол дуги в градусах,
a – угол дуги в радианах,
(pi) = 3,14.
Найти площадь сектора круга достаточно легко, зная основные формулы. Если дана длина дуги окружности и радиус сектора, то надо вспомнить формулу, из которой выводилась площадь самого круга, это была 

Более логичный способ вычислить площадь сектора круга – через угол и радиус. Всего круг имеет 360°, значит для того чтобы посчитать площадь определенной части круга, нужно всю площадь πr2 разделить на 360 и умножить на угол сектора в градусах.
Информация по назначению калькулятора
Сектор круга – это часть окружности внутри круга, состоящая из дуги вместе с ее двумя радиусами. Часть окружности (также известная как дуга) и 2 радиуса окружности встречаются в обеих конечных точках дуги, образуя сектор. Форма сектора круга выглядит как кусочек пиццы или пирога. В геометрии круг – одна из самых совершенных фигур. Форма сектора окружности – самая простая форма в геометрии. У него есть свои собственные различные части. Например, диаметр, радиус, окружность, сегмент, сектор.
Круг разделен на два сектора, и разделенные части известны как второстепенные сектора и главные сектора.
Большая часть круга является основным сектором, в то время как меньшая часть является второстепенным сектором.
В случае полукругов окружность делится на два сектора одинакового размера.
2 радиуса встречаются в части окружности круга, известной как дуга, образуя сектор окружности.
Онлайн калькулятор предназначен для нахождения параметров сектора круга, таких как:
- Площадь сектора
- Длина дуги
- Радиус
- Периметр сектора
- Центральный угол сектора в градусах и радианах
– это объем пространства, занимаемого в пределах границы сектора круга. Сектор всегда начинается с центра круга. Полукруг также является сектором круга, в данном случае круг имеет два сектора одинакового размера.
Можно найти зная радиус и центральный угол в градусах (Ssek = ( α / 360° ) * πr2)
– находится путем умножения радиуса на центральный угол сектора в радианах (L = r * α)
– равен сумме длины дуги и двум радиусам (Psek = L + r + r)
