Как найти площадь сектора сферы - Сайт, где вы сможете решить свои вопросы

Сфера, шар, сегмент и сектор. Формулы и свойства сферы

Определение.

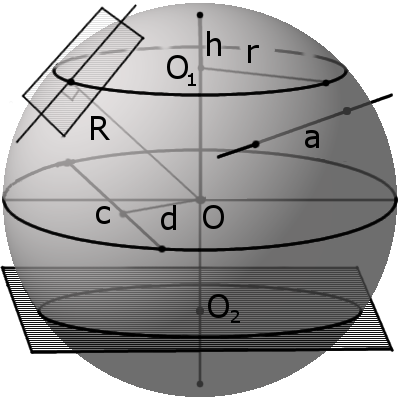
Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение. Радиус сферы (шара) (R) – это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара) (D) – это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула. Объём шара:

V =	4	πR³ =	1	πD³
3	6

Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4πR² = πD²

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:

x² + y² + z² = R²

2. Уравнение сферы с радиусом R и центром в точке с координатами (x₀, y₀, z₀) в декартовой системе координат:

(x – x₀)² + (y – y₀)² + (z – z₀)² = R²

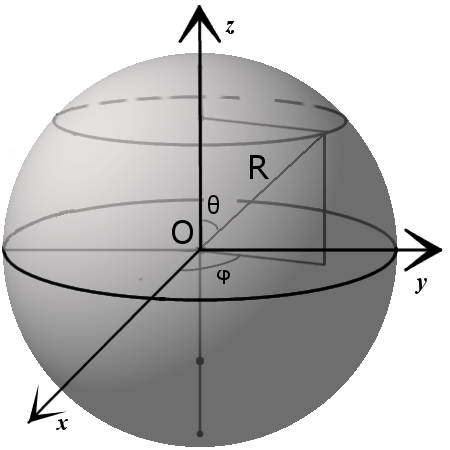
3. Параметрическое уравнение сферы с центром в точке (x₀, y₀, z₀):

x = x₀ + R · sin θ · cos φ
y = y₀ + R · sin θ · sin φ
z = z₀ + R · cos θ

где θ ϵ [0,π], φ ϵ [0,2π].

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы – это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) – это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость – это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость – это секущая плоскость, проходящая через центр сферы или шара, сечение образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

d < R

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m < R

Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R² – m²,

где R – радиус сферы (шара), m – расстояние от центра шара до секущей плоскости.

Определение. Полусфера (полушар) – это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение.Касательная к сфере – это прямая, которая касается сферы только в одной точке.

Определение.Касательная плоскость к сфере – это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

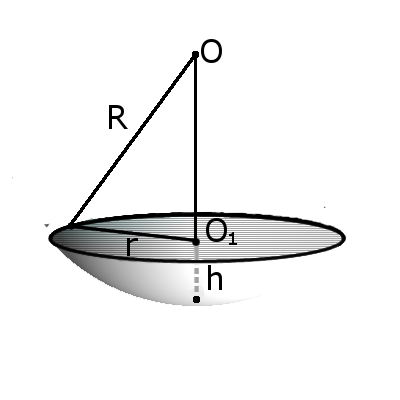
Определение. Сегмент шара – это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2πRh

Формула. Объём сегмента сферы с высотой h через радиус сферы R:

Определение. Срез шара – это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.

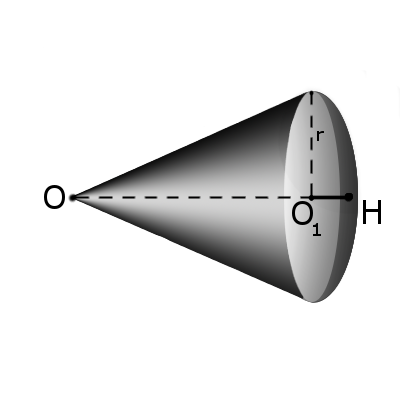
Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Формула. Площадь поверхности сектора S с высотой O₁H (h) через радиус шара OH (R):

S = πR(2h + √2hR – h²)

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.

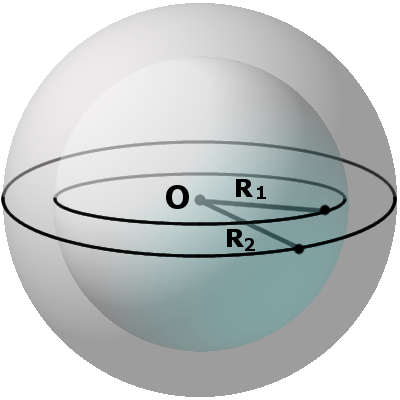
Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.

Источник

У этого термина существуют и другие значения, см. сегмент.

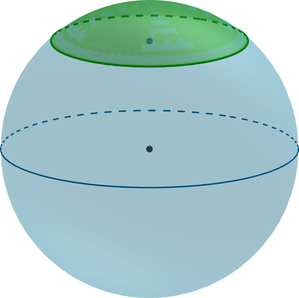
Пример сферического сегмента (окрашен синим цветом). Вторая половина сферы также представляет собой сферический сегмент

Сфери́ческий сегме́нт — поверхность, часть сферы, отсекаемая от неё некоторой плоскостью. Плоскость отсекает два сегмента: меньший сегмент называется также сферическим кругом^[1].
Если секущая плоскость проходит через центр сферы, то высота обоих сегментов равна радиусу сферы, и каждый из таких сферических сегментов называют полусферой.

Шарово́й сегме́нт — геометрическое тело, часть шара, отсекаемая от него некоторой плоскостью. Поверхностью шарового сегмента является объединение сферического сегмента и круга (основания шарового сегмента), границы которых совпадают.

Объём и площадь поверхности[править | править код]

Если радиус основания сегмента равен , высота сегмента равна , тогда объём шарового сегмента равен ^[2]

${displaystyle V={frac {pi h}{6}}(3a^{2}+h^{2}),}$

площадь поверхности сегмента равна

или

${displaystyle A=2pi r^{2}(1-cos theta ).}$

Параметры , и связаны соотношениями

${displaystyle r^{2}=(r-h)^{2}+a^{2}=r^{2}+h^{2}-2rh+a^{2},}$

${displaystyle r={frac {a^{2}+h^{2}}{2h}}.}$

Подстановка последнего выражения в первую формулу для вычисления площади приводит к равенству

${displaystyle A=2pi {frac {(a^{2}+h^{2})}{2h}}h=pi (a^{2}+h^{2}).}$

Заметим, что в верхней части сферы (синий сегмент на рисунке) ${displaystyle h=r-{sqrt {r^{2}-a^{2}}},}$ в нижней части сферы ${displaystyle h=r+{sqrt {r^{2}-a^{2}}},}$ следовательно, для обоих сегментов справедливо выражение и можно привести другое выражение для объёма:

${displaystyle V={frac {pi h^{2}}{3}}(3r-h).}$

Формула для определения объёма также может быть получена при интегрировании поверхности вращения:

${displaystyle V=int _{x}^{r}pi left(r^{2}-x^{2}right)dx=pi left({frac {2}{3}}r^{3}-r^{2}x+{frac {1}{3}}x^{3}right)={frac {pi }{3}}r^{3}(cos theta +2)(cos theta -1)^{2}.}$

Применение[править | править код]

Объём объединения и пересечения двух пересекающихся сфер[править | править код]

Объём объединения двух сфер радиусов r₁ и r₂ равен
^[3]

${displaystyle V=V^{(1)}-V^{(2)}}$

где

${displaystyle V^{(1)}={frac {4pi }{3}}r_{1}^{3}+{frac {4pi }{3}}r_{2}^{3}}$

является суммой объёмов двух сфер по отдельности, а

${displaystyle V^{(2)}={frac {pi h_{1}^{2}}{3}}(3r_{1}-h_{1})+{frac {pi h_{2}^{2}}{3}}(3r_{2}-h_{2})}$

является суммой объёмов двух сферических сегментов, образующих пересечение данных сфер. Пусть d < r₁ + r₂ — расстояние между центрами сфер, тогда исключение величин h₁ и h₂ приводит к выражению ^[4]^[5]

${displaystyle V^{(2)}={frac {pi }{12d}}(r_{1}+r_{2}-d)^{2}left(d^{2}+2d(r_{1}+r_{2})-3(r_{1}-r_{2})^{2}right).}$

Площадь поверхности, ограниченной кругами разных широт[править | править код]

Площадь поверхности, ограниченной кругами разных широт, является разностью площадей поверхности двух соответствующих сферических сегментов. Для сферы радиуса r и широт φ₁ и φ₂ данная площадь равна ^[6]

${displaystyle A=2pi r^{2}|sin varphi _{1}-sin varphi _{2}|.}$

Площадь квадратного участка поверхности шара[править | править код]

Участок, вырезанный на сфере радиуса r четырьмя дугами больших кругов, имеющими одинаковую угловую длину θ и попарно перпендикулярными (сферический квадрат, аналог квадрата на плоскости), имеет площадь

${displaystyle A=8r^{2}(1-cos theta /2).}$

Если угол θ мал (по сравнению с 1 радианом), то справедливо приближённое равенство, основывающееся на приближении ${displaystyle cos xto 1-x^{2}/2}$ при

${displaystyle Aapprox 8r^{2}{frac {theta ^{2}}{8}}=r^{2}theta ^{2}.}$

Например, площадь квадратного участка поверхности Земли (R_⊕ = 6378 км) со сторонами, равными 1 градусу, составляет

${displaystyle A(1^{circ })=8cdot R_{oplus }^{2}(1-cos 0{,}5^{circ })approx R_{oplus }^{2}cdot left({frac {pi }{180}}right)^{2}approx 12,391,{text{км}}^{2}.}$

1 квадратная секунда поверхности Земли имеет площадь в 3600² раз меньше: A(1′′) ≈ 12 391 км² / (60 · 60)² ≈ 956 м².

Обобщения[править | править код]

Сечения других тел[править | править код]

Сфероидальный сегмент получается при отсечении части сфероида таким образом, что она обладает круговой симметрией (обладает осью вращения). Аналогичным образом определяют эллипсоидальный сегмент.

Сегмент гиперсферы[править | править код]

Объём -мерного сегмента гиперсферы высотой и радиуса в -мерном евклидовом пространстве определяется по формуле ^[7]

${displaystyle V={frac {pi ^{frac {n-1}{2}},r^{n}}{,Gamma left({frac {n+1}{2}}right)}}int limits _{0}^{arccos left({frac {r-h}{r}}right)}sin ^{n}t,mathrm {d} t,}$

где Gamma (гамма-функция) задаётся выражением ${displaystyle Gamma (z)=int _{0}^{infty }t^{z-1}mathrm {e} ^{-t},mathrm {d} t.}$

Выражение для объёма можно переписать в терминах объёма единичного -мерного шара ${displaystyle C_{n}={pi ^{n/2}/Gamma left[1+{frac {n}{2}}right]}}$ и гипергеометрической функции ${displaystyle {}_{2}F_{1}}$ или регуляризованной неполной бета-функции ${displaystyle I_{x}(a,b)}$ как

${displaystyle V=C_{n},r^{n}left({frac {1}{2}},-,{frac {r-h}{r}},{frac {Gamma [1+{frac {n}{2}}]}{{sqrt {pi }},Gamma [{frac {n+1}{2}}]}}{,,}_{2}F_{1}left({tfrac {1}{2}},{tfrac {1-n}{2}};{tfrac {3}{2}};left({tfrac {r-h}{r}}right)^{2}right)right)={frac {1}{2}}C_{n},r^{n}I_{(2rh-h^{2})/r^{2}}left({frac {n+1}{2}},{frac {1}{2}}right).}$

Формула для площади поверхности может быть записана в терминах площади поверхности единичного -мерного шара ${displaystyle A_{n}={2pi ^{n/2}/Gamma left[{frac {n}{2}}right]}}$ как

${displaystyle A={frac {1}{2}}A_{n},r^{n-1}I_{(2rh-h^{2})/r^{2}}left({frac {n-1}{2}},{frac {1}{2}}right),}$

где

Также справедливы следующие формулы^[8]:
${displaystyle A=A_{n}p_{n-2}(q),quad V=V_{n}p_{n}(q),}$ где
${displaystyle q=1-h/r(0leq qleq 1),quad p_{n}(q)={frac {1-G_{n}(q)/G_{n}(1)}{2}},}$

${displaystyle G_{n}(q)=int limits _{0}^{q}(1-t^{2})^{(n-1)/2}dt.}$

При

${displaystyle G_{n}(q)=sum _{i=0}^{k}(-1)^{i}{binom {k}{i}}{frac {q^{2i+1}}{2i+1}}.}$

Было показано^[9], что при и ${displaystyle p_{n}(q)to 1-F({q{sqrt {n}}}),}$ где — стандартное нормальное распределение.

Литература[править | править код]

А. И. Маркушевич, А. Я. Хинчин, П. С. Александров. Основные понятия сферической геометрии // Энциклопедия элементарной математики. Книга 4 – Геометрия. — Москва: ГИФМЛ, 1963.

Примечания[править | править код]

Источник

В данной публикации мы рассмотрим формулу, с помощью которой можно вычислить площадь поверхности сектора шара, а также то, каким образом она получена.

Определение сектора шара
Формула для нахождения площади сектора шара

Определение сектора шара

Сектор шара (или шаровый сектор) – это часть шара, состоящая из шарового сегмента и конуса, вершиной которого является центр шара, а основанием – основание соответствующего сегмента. На рисунке ниже сектор закрашен оранжевым цветом.

R – радиус шара;
r – радиус основания сегмента и конуса;
h – высота сегмента; перпендикуляр от центра основания сегмента до точки на сфере.

Формула для нахождения площади сектора шара

Чтобы найти площадь поверхности шарового сектора необходимо сложить площади фигур, из которых он состоит: сферической поверхности соответствующего сегмента шара и боковой поверхности конуса.

S_{сфер. пов. сегмента} = 2πRh

S_{бок. пов. конуса} = πrR

S_{пов. шар. сектора} = 2πRh + πrR = πR(2h+r)

Примечания:

если вместо радиусов (R/r) известны соответствующие им диаметры (d), последние следует разделить на два, чтобы найти требуемые радиусы.
за значение π в формулах обычно принимается округленно значение, равное числу 3,14.

Источник

Площадь поверхности шарового сектора, формула

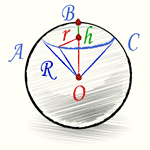
Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью основанием которой служит основание сегмента, а вершиной — центр шара.

Поверхность шарового сектора складывается из кривых поверхностей шарового сегмента и конуса.
Зная радиус основания сегмента и конуса r при помощи теоремы Пифагора и прямоугольного треугольника получим высоты
сегмента и конуса:

[ h_{конуса} = sqrt{R^2-r^2} ]

[ h_{сегмента} = R – sqrt{R^2-r^2} ]

Подставим формулы площади конуса и шарового сегмента:

[ S_{сектора} = S_{сегмента} + S_{конуса} ]

[ S_{сектора} = 2 pi R h_{сегмента} + pi R r ]

[ S_{сектора} = pi R ( 2 (R – sqrt{R^2-r^2}) + r ) ]

Формулы шара, сферы

Вычислить, найти площадь поверхности шарового сектора по формуле (5)

Площадь поверхности шарового сектора	стр. 317

Источник

({color{red}{{small{textbf{Факт 1. Про шаровой сегмент}}}}})
(bullet) Шаровой сегмент – шасть шара, отсекаемая от него плоскостью ((alpha)).

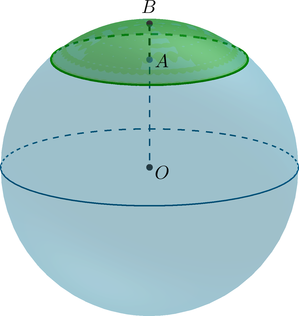
(bullet) Если (O) – центр шара, (OB=R) – радиус шара, перпендикулярный плоскости (alpha), (A) – центр круга (основания шарового сегмента), а также точка пересечения радиуса (OB) c этим кругом, то
(H=AB) – высота шарового сегмента.
(bullet) Площадь сферического сегмента (часть сферы, отсекаемая от нее плоскостью (alpha)) вычисляется по формуле [S=2pi cdot RH] (bullet) Объем шарового сегмента вычисляется по формуле [V=pi H^2cdot left(R-frac13Hright)]

({color{red}{{small{textbf{Факт 2. Про шаровой слой}}}}})
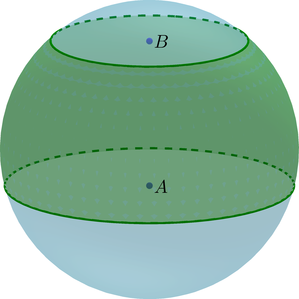
(bullet) Шаровой слой – часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.

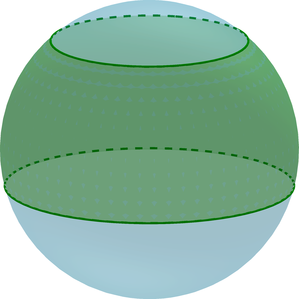
(bullet) Основания шарового слоя – это сечения шара плоскостями.
(bullet) Высота (H=AB) шарового слоя – это расстояние между основаниями.
(bullet) Площадь сферической части шарового слоя равна [S=2pi RH] где (R) – радиус шара.
(bullet) Объем шарового слоя равен разности объемов двух шаровых сегментов: [V=V_{A}-V_{B}]

({color{red}{{small{textbf{Факт 3. Про шаровой сектор}}}}})
(bullet) Шаровой сектор – часть шара, ограниченная сферической частью шарового сегмента и боковой поверхностью конуса, имеющего то же основание, что и шаровой сегмент.

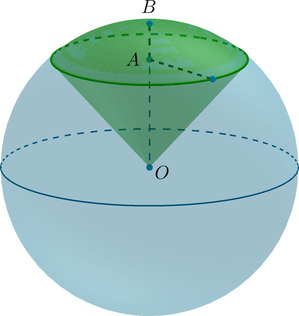
(bullet) Если (H=AB), то объем шарового сектора равен [V=dfrac23pi R^2cdot H]

Источник

Сфера, шар, сегмент и сектор. Формулы и свойства сферы

Уравнение сферы

Основные свойства сферы и шара

Секущая, хорда, секущая плоскость сферы и их свойства

Касательная, касательная плоскость к сфере и их свойства

Объём и площадь поверхности[править | править код]

Применение[править | править код]

Объём объединения и пересечения двух пересекающихся сфер[править | править код]

Площадь поверхности, ограниченной кругами разных широт[править | править код]

Площадь квадратного участка поверхности шара[править | править код]

Обобщения[править | править код]

Сечения других тел[править | править код]

Сегмент гиперсферы[править | править код]

Литература[править | править код]

Примечания[править | править код]

Определение сектора шара

Формула для нахождения площади сектора шара

Площадь поверхности шарового сектора, формула

Формулы шара, сферы

Вычислить, найти площадь поверхности шарового сектора по формуле (5)

Площадь поверхности шарового сектора

Вам также может понравиться

Как найти периметр с помощью координат

Как исправить ошибку доступа 403

Как найти подход к женатому мужчине

Добавить комментарий Отменить ответ