Как найти площадь сердца

Как найти площадь сердца

Площадь формы сердца Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Длина края квадрата в форме сердца: 10 метр –> 10 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

178.539816339745 Квадратный метр –> Конверсия не требуется




4 Площадь формы сердца Калькуляторы

Площадь формы сердца формула

Площадь формы сердца = (1+pi/4)*Длина края квадрата в форме сердца^2

A = (1+pi/4)*le(Square)^2

Что такое форма сердца?

Кривая сердца представляет собой замкнутую кривую, имеющую форму сердца. Сердце хорошо известно как фигура на игральных картах помимо бубнов, крестов и пик. Если вы говорите о сердце, вы скорее имеете в виду фигуру сердца, чем кривую в форме сердца. Это сердце основано на квадрате, стоящем на одном кончике. На каждой из его двух верхних сторон прикреплен соответствующий полукруг.

Источник

From Wikipedia, the free encyclopedia

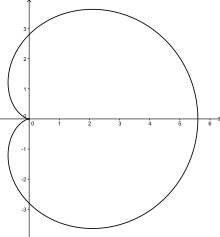
The caustic appearing on the surface of this cup of coffee is a cardioid.

In geometry, a cardioid (from Greek καρδιά (kardiá) ‘heart’) is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion.[1] A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle.[2]

Cardioid generated by a rolling circle on a circle with the same radius

The name was coined by Giovanni Salvemini in 1741[3] but the cardioid had been the subject of study decades beforehand.[4] Although named for its heart-like form, it is shaped more like the outline of the cross-section of a round apple without the stalk.

A cardioid microphone exhibits an acoustic pickup pattern that, when graphed in two dimensions, resembles a cardioid (any 2d plane containing the 3d straight line of the microphone body). In three dimensions, the cardioid is shaped like an apple centred around the microphone which is the “stalk” of the apple.

Equations[edit]

Generation of a cardioid and the coordinate system used

Let a be the common radius of the two generating circles with midpoints {displaystyle (-a,0),(a,0)}, varphi the rolling angle and the origin the starting point (see picture). One gets the

  • parametric representation:

    {displaystyle {begin{aligned}x(varphi )&=2a(1-cos varphi )cdot cos varphi ,\y(varphi )&=2a(1-cos varphi )cdot sin varphi ,qquad 0leq varphi <2pi end{aligned}}}

    and herefrom the representation in

  • polar coordinates:

    {displaystyle r(varphi )=2a(1-cos varphi ).}

  • Introducing the substitutions {displaystyle cos varphi =x/r} and {textstyle r={sqrt {x^{2}+y^{2}}}} one gets after removing the square root the implicit representation in Cartesian coordinates:

    {displaystyle left(x^{2}+y^{2}right)^{2}+4axleft(x^{2}+y^{2}right)-4a^{2}y^{2}=0.}

Proof for the parametric representation[edit]

A proof can be established using complex numbers and their common description as the complex plane. The rolling movement of the black circle on the blue one can be split into two rotations. In the complex plane a rotation around point {displaystyle 0} (the origin) by an angle varphi can be performed by multiplying a point z (complex number) by {displaystyle e^{ivarphi }}. Hence

the rotation {displaystyle Phi _{+}} around point a is{displaystyle :zmapsto a+(z-a)e^{ivarphi }},
the rotation {displaystyle Phi _{-}} around point -a is: {displaystyle zmapsto -a+(z+a)e^{ivarphi }}.

A point p(varphi ) of the cardioid is generated by rotating the origin around point a and subsequently rotating around -a by the same angle varphi :

{displaystyle p(varphi )=Phi _{-}(Phi _{+}(0))=Phi _{-}left(a-ae^{ivarphi }right)=-a+left(a-ae^{ivarphi }+aright)e^{ivarphi }=a;left(-e^{i2varphi }+2e^{ivarphi }-1right).}

From here one gets the parametric representation above:

{displaystyle {begin{array}{cclcccc}x(varphi )&=&a;(-cos(2varphi )+2cos varphi -1)&=&2a(1-cos varphi )cdot cos varphi &&\y(varphi )&=&a;(-sin(2varphi )+2sin varphi )&=&2a(1-cos varphi )cdot sin varphi &.&end{array}}}

(The trigonometric identities {displaystyle e^{ivarphi }=cos varphi +isin varphi , (cos varphi )^{2}+(sin varphi )^{2}=1,} {displaystyle cos(2varphi )=(cos varphi )^{2}-(sin varphi )^{2},} and {displaystyle sin(2varphi )=2sin varphi cos varphi } were used.)

Metric properties[edit]

For the cardioid as defined above the following formulas hold:

The proofs of these statement use in both cases the polar representation of the cardioid. For suitable formulas see polar coordinate system (arc length) and polar coordinate system (area)

Proof of the area formula

{displaystyle A=2cdot {tfrac {1}{2}}int _{0}^{pi }{(r(varphi ))^{2}};dvarphi =int _{0}^{pi }{4a^{2}(1-cos varphi )^{2}};dvarphi =cdots =4a^{2}cdot {tfrac {3}{2}}pi =6pi a^{2}.}

Proof of the arc length formula

{displaystyle L=2int _{0}^{pi }{sqrt {r(varphi )^{2}+(r'(varphi ))^{2}}};dvarphi =cdots =8aint _{0}^{pi }{sqrt {{tfrac {1}{2}}(1-cos varphi )}};dvarphi =8aint _{0}^{pi }sin left({tfrac {varphi }{2}}right)dvarphi =16a.}

Proof for the radius of curvature

The radius of curvature rho of a curve in polar coordinates with equation {displaystyle r=r(varphi )} is (s. curvature)

{displaystyle rho (varphi )={frac {left[r(varphi )^{2}+{dot {r}}(varphi )^{2}right]^{3/2}}{r(varphi )^{2}+2{dot {r}}(varphi )^{2}-r(varphi ){ddot {r}}(varphi )}} .}

For the cardioid {displaystyle r(varphi )=2a(1-cos varphi )=4asin ^{2}left({tfrac {varphi }{2}}right)} one gets

{displaystyle rho (varphi )=cdots ={frac {left[16a^{2}sin ^{2}{frac {varphi }{2}}right]^{frac {3}{2}}}{24a^{2}sin ^{2}{frac {varphi }{2}}}}={frac {8}{3}}asin {frac {varphi }{2}} .}

Properties[edit]

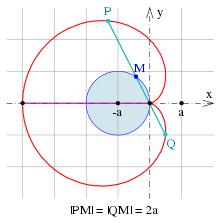
Chords through the cusp[edit]

C1
Chords through the cusp of the cardioid have the same length 4a.
C2
The midpoints of the chords through the cusp lie on the perimeter of the fixed generator circle (see picture).

Proof of C1[edit]

The points {displaystyle P:p(varphi ),;Q:p(varphi +pi )} are on a chord through the cusp (=origin). Hence

{displaystyle {begin{aligned}|PQ|&=r(varphi )+r(varphi +pi )\&=2a(1-cos varphi )+2a(1-cos(varphi +pi ))=cdots =4aend{aligned}}.}

Proof for C2[edit]

For the proof the representation in the complex plane (see above) is used. For the points

{displaystyle P: p(varphi )=a,left(-e^{i2varphi }+2e^{ivarphi }-1right)}

and

{displaystyle Q: p(varphi +pi )=a,left(-e^{i2(varphi +pi )}+2e^{i(varphi +pi )}-1right)=a,left(-e^{i2varphi }-2e^{ivarphi }-1right),}

the midpoint of the chord PQ is

{displaystyle M: {tfrac {1}{2}}(p(varphi )+p(varphi +pi ))=cdots =-a-ae^{i2varphi }}

which lies on the perimeter of the circle with midpoint -a and radius a (see picture).

Cardioid as inverse curve of a parabola[edit]

Cardioid generated by the inversion of a parabola across the unit circle (dashed)

A cardioid is the inverse curve of a parabola with its focus at the center of inversion (see graph)

For the example shown in the graph the generator circles have radius {textstyle a={frac {1}{2}}}. Hence the cardioid has the polar representation

{displaystyle r(varphi )=1-cos varphi }

and its inverse curve

{displaystyle r(varphi )={frac {1}{1-cos varphi }},}

which is a parabola (s. parabola in polar coordinates) with the equation {textstyle x={tfrac {1}{2}}left(y^{2}-1right)} in Cartesian coordinates.

Remark: Not every inverse curve of a parabola is a cardioid. For example, if a parabola is inverted across a circle whose center lies at the vertex of the parabola, then the result is a cissoid of Diocles.

Cardioid as envelope of a pencil of circles[edit]

Cardioid as envelope of a pencil of circles

In the previous section if one inverts additionally the tangents of the parabola one gets a pencil of circles through the center of inversion (origin). A detailed consideration shows: The midpoints of the circles lie on the perimeter of the fixed generator circle. (The generator circle is the inverse curve of the parabola’s directrix.)

This property gives rise to the following simple method to draw a cardioid:

  1. Choose a circle c and a point O on its perimeter,
  2. draw circles containing O with centers on c, and
  3. draw the envelope of these circles.

Proof with envelope condition

The envelope of the pencil of implicitly given curves

{displaystyle F(x,y,t)=0}

with parameter t consists of such points (x,y) which are solutions of the non-linear system

{displaystyle F(x,y,t)=0,quad F_{t}(x,y,t)=0,}

which is the envelope condition. Note that F_t means the partial derivative for parameter t.

Let c be the circle with midpoint (-1,0) and radius 1. Then c has parametric representation {displaystyle (-1+cos t,sin t)}. The pencil of circles with centers on c containing point {displaystyle O=(0,0)} can be represented implicitly by

{displaystyle F(x,y,t)=(x+1-cos t)^{2}+(y-sin t)^{2}-(2-2cos t)=0,}

which is equivalent to

{displaystyle F(x,y,t)=x^{2}+y^{2}+2x;(1-cos t)-2y;sin t=0;.}

The second envelope condition is

{displaystyle F_{t}(x,y,t)=2x;sin t-2y;cos t=0.}

One easily checks that the points of the cardioid with the parametric representation

{displaystyle x(t)=2(1-cos t)cos t,quad y(t)=2(1-cos t)sin t}

fulfill the non-linear system above. The parameter t is identical to the angle parameter of the cardioid.

Cardioid as envelope of a pencil of lines[edit]

Cardioid as envelope of a pencil of lines

A similar and simple method to draw a cardioid uses a pencil of lines. It is due to L. Cremona:

  1. Draw a circle, divide its perimeter into equal spaced parts with 2N points (s. picture) and number them consecutively.
  2. Draw the chords: {displaystyle (1,2),(2,4),dots ,(n,2n),dots ,(N,2N),(N+1,2),(N+2,4),dots }. (That is, the second point is moved by double velocity.)
  3. The envelope of these chords is a cardioid.

Cremona’s generation of a cardioid

Proof[edit]

The following consideration uses trigonometric formulae for {displaystyle cos alpha +cos beta }, {displaystyle sin alpha +sin beta }, {displaystyle 1+cos 2alpha }, {displaystyle cos 2alpha }, and {displaystyle sin 2alpha }.
In order to keep the calculations simple, the proof is given for the cardioid with polar representation
{displaystyle r=2(1mathbin {color {red}+} cos varphi )} (§ Cardioids in different positions).

Equation of the tangent of the cardioid with polar representation {displaystyle r=2(1+cos varphi )}[edit]

From the parametric representation

{displaystyle {begin{aligned}x(varphi )&=2(1+cos varphi )cos varphi ,\y(varphi )&=2(1+cos varphi )sin varphi end{aligned}}}

one gets the normal vector {displaystyle {vec {n}}=left({dot {y}},-{dot {x}}right)^{mathsf {T}}}. The equation of the tangent
{displaystyle {dot {y}}(varphi )cdot (x-x(varphi ))-{dot {x}}(varphi )cdot (y-y(varphi ))=0} is:

{displaystyle (cos 2varphi +cos varphi )cdot x+(sin 2varphi +sin varphi )cdot y=2(1+cos varphi )^{2},.}

With help of trigonometric formulae and subsequent division by {textstyle cos {frac {1}{2}}varphi }, the equation of the tangent can be rewritten as:

{displaystyle cos({tfrac {3}{2}}varphi )cdot x+sin left({tfrac {3}{2}}varphi right)cdot y=4left(cos {tfrac {1}{2}}varphi right)^{3}quad 0<varphi <2pi , varphi neq pi .}

Equation of the chord of the circle with midpoint (1,0) and radius 3[edit]

For the equation of the secant line passing the two points {displaystyle (1+3cos theta ,3sin theta ), (1+3cos {color {red}2}theta ,3sin {color {red}2}theta ))} one gets:

{displaystyle (sin theta -sin 2theta )x+(cos 2theta -sin theta )y=-2cos theta -sin(2theta ),.}

With help of trigonometric formulae and the subsequent division by {textstyle sin {frac {1}{2}}theta } the equation of the secant line can be rewritten by:

{displaystyle cos left({tfrac {3}{2}}theta right)cdot x+sin left({tfrac {3}{2}}theta right)cdot y=4left(cos {tfrac {1}{2}}theta right)^{3}quad 0<theta <2pi .}

Conclusion[edit]

Despite the two angles {displaystyle varphi ,theta } have different meanings (s. picture) one gets for {displaystyle varphi =theta } the same line. Hence any secant line of the circle, defined above, is a tangent of the cardioid, too:

The cardioid is the envelope of the chords of a circle.

Remark:
The proof can be performed with help of the envelope conditions (see previous section) of an implicit pencil of curves:

{displaystyle F(x,y,t)=cos left({tfrac {3}{2}}tright)x+sin left({tfrac {3}{2}}tright)y-4left(cos {tfrac {1}{2}}tright)^{3}=0}

is the pencil of secant lines of a circle (s. above) and

{displaystyle F_{t}(x,y,t)=-{tfrac {3}{2}}sin left({tfrac {3}{2}}tright)x+{tfrac {3}{2}}cos left({tfrac {3}{2}}tright)y+3cos left({tfrac {1}{2}}tright)sin t=0,.}

For fixed parameter t both the equations represent lines. Their intersection point is

{displaystyle x(t)=2(1+cos t)cos t,quad y(t)=2(1+cos t)sin t,}

which is a point of the cardioid with polar equation {displaystyle r=2(1+cos t).}

Cardioid as caustic: light source Z, light ray {vec {s}}, reflected ray {vec {r}}

Cardioid as caustic of a circle with light source (right) on the perimeter

Cardioid as caustic of a circle[edit]

The considerations made in the previous section give a proof that the caustic of a circle with light source on the perimeter of the circle is a cardioid.

If in the plane there is a light source at a point Z on the perimeter of a circle which is reflecting any ray, then the reflected rays within the circle are tangents of a cardioid.

Proof

As in the previous section the circle may have midpoint {displaystyle (1,0)} and radius 3. Its parametric representation is

{displaystyle c(varphi )=(1+3cos varphi ,3sin varphi ) .}

The tangent at circle point {displaystyle C: k(varphi )} has normal vector {displaystyle {vec {n}}_{t}=(cos varphi ,sin varphi )^{mathsf {T}}}. Hence the reflected ray has the normal vector {displaystyle {vec {n}}_{r}=left(cos {color {red}{tfrac {3}{2}}}varphi ,sin {color {red}{tfrac {3}{2}}}varphi right)^{mathsf {T}}} (see graph) and contains point {displaystyle C: (1+3cos varphi ,3sin varphi )}. The reflected ray is part of the line with equation (see previous section)

{displaystyle cos left({tfrac {3}{2}}varphi right)x+sin left({tfrac {3}{2}}varphi right)y=4left(cos {tfrac {1}{2}}varphi right)^{3},,}

which is tangent of the cardioid with polar equation

{displaystyle r=2(1+cos varphi )}

from the previous section.

Remark: For such considerations usually multiple reflections at the circle are neglected.

Cardioid as pedal curve of a circle[edit]

Point of cardioid is foot of dropped perpendicular on tangent of circle

The Cremona generation of a cardioid should not be confused with the following generation:

Let be k a circle and O a point on the perimeter of this circle. The following is true:

The foots of perpendiculars from point O on the tangents of circle k are points of a cardioid.

Hence a cardioid is a special pedal curve of a circle.

Proof[edit]

In a Cartesian coordinate system circle k may have midpoint {displaystyle (2a,0)} and radius 2a. The tangent at circle point {displaystyle (2a+2acos varphi ,2asin varphi )} has the equation

{displaystyle (x-2a)cdot cos varphi +ycdot sin varphi =2a,.}

The foot of the perpendicular from point O on the tangent is point {displaystyle (rcos varphi ,rsin varphi )} with the still unknown distance r to the origin O. Inserting the point into the equation of the tangent yields

{displaystyle (rcos varphi -2a)cos varphi +rsin ^{2}varphi =2aquad rightarrow quad r=2a(1+cos varphi )}

which is the polar equation of a cardioid.

Remark: If point O is not on the perimeter of the circle k, one gets a limaçon of Pascal.

The evolute of a cardioid[edit]

  A cardioid

  Evolute of the cardioid

  One point P; its centre of curvature M; and its osculating circle.

The evolute of a curve is the locus of centers of curvature. In detail: For a curve {displaystyle {vec {x}}(s)={vec {c}}(s)} with radius of curvature {displaystyle rho (s)} the evolute has the representation

{displaystyle {vec {X}}(s)={vec {c}}(s)+rho (s){vec {n}}(s).}

with {displaystyle {vec {n}}(s)} the suitably oriented unit normal.

For a cardioid one gets:

The evolute of a cardioid is another cardioid, one third as large, and facing the opposite direction (s. picture).

Proof[edit]

For the cardioid with parametric representation

{displaystyle x(varphi )=2a(1-cos varphi )cos varphi =4asin ^{2}{tfrac {varphi }{2}}cos varphi ,,}

{displaystyle y(varphi )=2a(1-cos varphi )sin varphi =4asin ^{2}{tfrac {varphi }{2}}sin varphi }

the unit normal is

{displaystyle {vec {n}}(varphi )=(-sin {tfrac {3}{2}}varphi ,cos {tfrac {3}{2}}varphi )}

and the radius of curvature

{displaystyle rho (varphi )={tfrac {8}{3}}asin {tfrac {varphi }{2}},.}

Hence the parametric equations of the evolute are

{displaystyle X(varphi )=4asin ^{2}{tfrac {varphi }{2}}cos varphi -{tfrac {8}{3}}asin {tfrac {varphi }{2}}cdot sin {tfrac {3}{2}}varphi =cdots ={tfrac {4}{3}}acos ^{2}{tfrac {varphi }{2}}cos varphi -{tfrac {4}{3}}a,,}

{displaystyle Y(varphi )=4asin ^{2}{tfrac {varphi }{2}}sin varphi +{tfrac {8}{3}}asin {tfrac {varphi }{2}}cdot cos {tfrac {3}{2}}varphi =cdots ={tfrac {4}{3}}acos ^{2}{tfrac {varphi }{2}}sin varphi ,.}

These equations describe a cardioid a third as large, rotated 180 degrees and shifted along the x-axis by {displaystyle -{tfrac {4}{3}}a}.

(Trigonometric formulae were used: {displaystyle sin {tfrac {3}{2}}varphi =sin {tfrac {varphi }{2}}cos varphi +cos {tfrac {varphi }{2}}sin varphi , cos {tfrac {3}{2}}varphi =cdots , sin varphi =2sin {tfrac {varphi }{2}}cos {tfrac {varphi }{2}}, cos varphi =cdots .})

Orthogonal trajectories[edit]

An orthogonal trajectory of a pencil of curves is a curve which intersects any curve of the pencil orthogonally. For cardioids the following is true:

The orthogonal trajectories of the pencil of cardioids with equations

{displaystyle r=2a(1-cos varphi ) ,;a>0 , }

are the cardioids with equations

{displaystyle r=2b(1+cos varphi ) ,;b>0 .}

(The second pencil can be considered as reflections at the y-axis of the first one. See diagram.)

Proof[edit]

For a curve given in polar coordinates by a function {displaystyle r(varphi )} the following connection to Cartesian coordinates hold:

{displaystyle {begin{aligned}x(varphi )&=r(varphi )cos varphi ,,\y(varphi )&=r(varphi )sin varphi end{aligned}}}

and for the derivatives

{displaystyle {begin{aligned}{frac {dx}{dvarphi }}&=r'(varphi )cos varphi -r(varphi )sin varphi ,,\{frac {dy}{dvarphi }}&=r'(varphi )sin varphi +r(varphi )cos varphi ,.end{aligned}}}

Dividing the second equation by the first yields the Cartesian slope of the tangent line to the curve at the point {displaystyle (r(varphi ),varphi )}:

{displaystyle {frac {dy}{dx}}={frac {r'(varphi )sin varphi +r(varphi )cos varphi }{r'(varphi )cos varphi -r(varphi )sin varphi }}.}

For the cardioids with the equations {displaystyle r=2a(1-cos varphi );} and {displaystyle r=2b(1+cos varphi ) } respectively one gets:

{displaystyle {frac {dy_{a}}{dx}}={frac {cos(varphi )-cos(2varphi )}{sin(2varphi )-sin(varphi )}}}

and

{displaystyle {frac {dy_{b}}{dx}}=-{frac {cos(varphi )+cos(2varphi )}{sin(2varphi )+sin(varphi )}} .}

(The slope of any curve depends on varphi only, and not on the parameters a or b!)

Hence

{displaystyle {frac {dy_{a}}{dx}}cdot {frac {dy_{b}}{dx}}=cdots =-{frac {cos ^{2}varphi -cos ^{2}(2varphi (}{sin ^{2}(2varphi )-sin ^{2}varphi }}=-{frac {-1+cos ^{2}varphi +1-cos ^{2}2varphi }{sin ^{2}(2varphi )-sin ^{2}(varphi )}}=-1,.}

That means: Any curve of the first pencil intersects any curve of the second pencil orthogonally.

4 cardioids in polar representation and their position in the coordinate system

In different positions[edit]

Choosing other positions of the cardioid within the coordinate system results in different equations. The picture shows the 4 most common positions of a cardioid and their polar equations.

In complex analysis[edit]

In complex analysis, the image of any circle through the origin under the map {displaystyle zto z^{2}} is a cardioid. One application of this result is that the boundary of the central period-1 component of the Mandelbrot set is a cardioid given by the equation

{displaystyle c,=,{frac {1-left(e^{it}-1right)^{2}}{4}}.}

The Mandelbrot set contains an infinite number of slightly distorted copies of itself and the central bulb of any of these smaller copies is an approximate cardioid.

Cardioid formed by light on a watch dial.

Caustics[edit]

Certain caustics can take the shape of cardioids. The catacaustic of a circle with respect to a point on the circumference is a cardioid. Also, the catacaustic of a cone with respect to rays parallel to a generating line is a surface whose cross section is a cardioid. This can be seen, as in the photograph to the right, in a conical cup partially filled with liquid when a light is shining from a distance and at an angle equal to the angle of the cone.[5] The shape of the curve at the bottom of a cylindrical cup is half of a nephroid, which looks quite similar.

Generating a cardioid as pedal curve of a circle

See also[edit]

  • Limaçon
  • Nephroid
  • Deltoid
  • Wittgenstein’s rod
  • Cardioid microphone
  • Lemniscate of Bernoulli
  • Loop antenna
  • Radio direction finder
  • Radio direction finding
  • Yagi antenna
  • Giovanni Salvemini

Notes[edit]

  1. ^ Weisstein, Eric W. “Parabola Inverse Curve”. MathWorld.
  2. ^ S Balachandra Rao . Differential Calculus, p. 457
  3. ^ Lockwood
  4. ^ Yates
  5. ^ “Surface Caustique” at Encyclopédie des Formes Mathématiques Remarquables

References[edit]

  • R.C. Yates (1952). “Cardioid”. A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards. pp. 4 ff.
  • Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. 24–25. ISBN 0-14-011813-6.

External links[edit]

Wikimedia Commons has media related to Cardioids.

  • “Cardioid”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
  • O’Connor, John J.; Robertson, Edmund F., “Cardioid”, MacTutor History of Mathematics archive, University of St Andrews
  • Hearty Munching on Cardioids at cut-the-knot
  • Weisstein, Eric W. “Cardioid”. MathWorld.
  • Weisstein, Eric W. “Epicycloid–1-Cusped”. MathWorld.
  • Weisstein, Eric W. “Heart Curve”. MathWorld.
  • Xah Lee, Cardioid (1998) (This site provides a number of alternative constructions).
  • Jan Wassenaar, Cardioid, (2005)
Источник

Mariam06Hani

+30

Ответ дан

1 месяц назад

Математика

1 – 4 классы

Нужно найти площадь сердца. Спасибо.

Ответ

5/5
(1 оценка)

1

vasilevanatasa4

vasilevanatasa4
1 месяц назад

Светило науки – 6 ответов – 0 раз оказано помощи

Ответ:

площадь сердца 9 квадратных сантиметров

Оцените пользу ответа

Мозг
Отвечающий

Остались вопросы?

Задать вопрос

Источник

«Если человек в школе не научится творить,
то и в жизни он будет только
подражать и копировать».   

Л.Н.Толстой.

9 класс. Тема: Площадь круга

(учебник: Л.С. Атанасян, Геометрия 7-9)

Урок решения практических, проектно-исследовательских задач.

Урок по теме заключительный.

Цель:

Деятельностная: формирование у учащихся способностей к обобщению, структурированию и систематизации изученной темы.

Образовательная: систематизация учебного материала, аргументация и систематизация обнаруженных фактов.

Задачи урока:

Образовательные задачи: приобретение учащимися исследовательских знаний и умений: знаний специфики и особенностей процесса научного познания, ступеней исследовательской деятельности, методики научного исследования; формирование знаний по нахождению площади нестандартных геометрических фигур.

Развивающие задачи: формирование умений выделять проблемы, формулировать гипотезы, планировать эксперимент в соответствии с гипотезой, интегрировать данные, делать вывод.

Воспитательные задачи: развитие активного внимания, творческого мышления, самоориентации, развитие межличностного общения в паре.

Постановка учебной проблемы – подводящий к теме диалог. Он представляет собой систему посильных ученику вопросов и заданий, которые шаг за шагом приводят ученика к осознанию темы урока.

В структуру подводящего диалога могут входить задания:

  • репродуктивные (вспомни формулы, выполни уже привычное)
  • мыслительные (проанализируй, сравни)

Последний вопрос учителя обязательно будет на обобщение, а ответом на него станет формулировка учебной проблемы: как по данному рисунку вычислить площадь закрашенной фигуры.

Парная работа: пара планирует свою деятельность, распределяет обязанности и приступает к работе.

Учащиеся 9 класса имеют раздаточный материал по нахождению площадей нестандартных геометрических фигур.

Оборудование: доска SMART, презентация, раздаточный материал.

Важно акцентировать внимание выпускников на том, что они самостоятельно нашли алгоритм по вычислению площади закрашенной фигуры.

Необходимо дать возможность каждому ученику почувствовать важность его участия в процессе урока (так как учитываются рассуждения всех участников), развивать межличностное общение в паре, учить необходимости подчинять свои действия поставленной задачи и доводить начатую работу до конца. В решении проблем растет и развивается личность.

На уроке используется технология личностно-ориентированного обучения, ИКТ- использование новых педагогических инструментов таких как: интерактив, коммуникативность, производительность; исследовательский метод, учащиеся ориентируются в видах исследовательской деятельности и овладевают поисковыми методами.

Геометрическая сказка «В мире площадей»

Слушая математическую сказку, будем решать задачи на нахождение площадей разных геометрических фигур.

Часть 1.

Для того чтобы вырастить цветок, нужно вспахать землю и бросить в нее зерно. Только благодаря заботе и долгому уходу можно вырастить то, что потом будет радовать глаз красотой и совершенством. Давайте и мы бросим «зерно мысли» в поле площадей.

Для начала найдем площадь «зерна», расположенного в квадрате с длиной стороны a.

1.gif

Часть 2.

Но вот зернышко брошено в землю, оно проросло, появился цветок. Контуры цветка расположены в квадрате, определим его площадь.

2.gif

Интересно, что ответы получились одинаковые, но еще много таинственных неожиданностей.

Часть 3.

Изрядно потрудившись, надо отдохнуть. Приложим голову к «подушке» и найдем ее площадь.

3.gif

Часть 4.

Отдохнув, мы отправляемся дальше. Кругом простираются зеленые леса и голубые озера. И вдруг на поверхности голубого озера мы видим серебряную рыбку, которая плещется в воде. Игривая рыбка поразила нас своей изящной формой и заставила задуматься о площади.

4.gif

Часть 5.

Рыбка вильнула хвостом и уплыла. И тут мы заметили неподалеку красивый домик похожий на грибок. Дом стоял на высоком холме. Солнечные лучи грели его хрустальную крышу, отражаясь от нее сотнями золотых бликов. Необъяснимая сила тянула к «грибку». Это было желание скорее найти площадь домика без окна, мы стали решать задачу.

5.gif

Часть 6.

Мы восхищались домиком с упоением. Но казалось, что хрустальный дворец вот – вот исчезнет. Прошло какое-то время, прежде чем нам удалось все отчетливо рассмотреть. Из дома вышла улыбающаяся девушка в разноцветном «фартуке». У нее была приветливая лучистая улыбка, добрый завораживающий взгляд. Мы познакомились с хозяйкой, имя у нее необычное – Площания. Мы стали разговаривать с хозяйкой о проделанном путешествии, незаметно, окинув взглядом фартук, нашли его площадь.

6.gif

Часть 7.

Потом сидели за большим столом, принимали угощения Площании, решали задачи, рассказывали о себе. Нам не хотелось уходить из этого уютного, теплого и красивого дома с хрустальной крышей, сердце наше переполнялось радостью. Давайте найдем площадь нашего сердца.

8.gif

Часть 8. Домашнее задание.

Нам надо торопиться домой. Еще раз, посмотрев на домик – «грибок» мы устремились вперед по дорожке, ведущей к озеру. По пути увидели квадратную клумбу, на которой рос один единственный цветок, он был симметричным и совсем не похож на другие земные цветки. Теперь нам стало понятно, что всё состояло из геометрических фигур. Восторгаясь творениями неизвестного сказочника, вы определите элементы симметрии цветка – центр и ось симметрии и найдите его площадь.

7.gif

Учащиеся совершенно самостоятельно выдвигают свои гипотезы по нахождению площади фигур (варианты могут быть различные), пользуясь знаниями формул геометрических фигур, находят пути решения проблем поставленных на каждом этапе урока.

Рефлексия: Вернуться к поставленной проблеме (Как по данному рисунку вычислить площадь закрашенной фигуры)

  • выделить геометрические фигуры на рисунке, площадь которых знаем;
  • в зависимости от геометрических фигур необходимо сконструировать закрашенную фигуру;
  • применить известные формулы геометрических фигур.

Какие ключевые слова сегодня на уроке использовались?

Квадрат, сторона квадрата, радиус, круг, сектор, площадь.

Таким образом, можно утверждать, что детская работа по конструированию нестандартных фигур строится по законам настоящей исследовательской научной работы.

Литература

  1. А.Азевич. В мире площадей. Газета “Математика” Издательского дома “Первое сентября” №8,1997.
  2. Атанасян А.С.Геометрия 7-9 (учебник для учащихся общеобразовательных учреждений) /– А.С.Атанасян М.: Просвещение, 2013.

Раздаточный материал

«В мире площадей»

Цель: Выработать алгоритм нахождения площади нестандартной геометрической фигуры и безошибочно применять формулы при вычислении площади геометрических фигур.

Парная работа: пара планирует свою деятельность, распределяет обязанности и приступает к работе.

Инструкция:

  • внимательно слушать рассказ учителя;
  • рассмотреть рисунок;
  • по данному рисунку вычислить площадь закрашенной фигуры;
  • выполнить конструирование на рисунке;
  • применить знания формул площадей геометрических фигур;
  • выполнить вычисление на листе.
  1. Найдите площадь «зерна», расположенного в квадрате с длиной стороны a.

1.gif =

  1. Найдите площадь «цветка», расположенного в квадрате с длиной стороны a.

2.gif =

  1. Найдите площадь «подушки», расположенной в квадрате с длиной стороны a.

3.gif

  1. Найдите площадь «рыбки», расположенной в квадрате с длиной стороны a.

4.gif

=

  1. Найдите площадь «домика», расположенного в квадрате с длиной стороны a.

5.gif

  1. Найдите площадь «фартука», расположенного в квадрате с длиной стороны a.

6.gif

  1. Найдите площадь «сердца», расположенного в квадрате с длиной стороны a.

8.gif =

Домашнее задание: Найдите площадь «цветка», расположенного в квадрате с длиной стороны a.

7.gif

Источник

Площадь сердца в передней проекции


admin1
Медицинские советы и статьи
12.03.2020

Размеры каждого желудочка определяются измерением перпендикуляра от перегородки до наиболее отдаленных от нее контуров желудочков; разделив расстояние ГД на 4, определяем, каким должен быть размер желудочков у данного больного,- так называемый вычисленный размер желудочков. Истинные размеры желудочков в норме должны равняться вычисленным с некоторым преобладанием левого желудочка. В практике часто встречаются случаи, когда в силу условно принятого угла поворота 50; линия А Б не равняется линии БВ, а каким-то отрезком (ВХ) выступает на левое реберно-позвоночное сочленение. Этот отрезок следует перенести за линию ГД вправо от реберно-позвоночного сочленения (ДХ). Нижний край перегородки в этих случаях определяется с учетом добавленного отрезка. Различают три степени увеличения желудочков порею. В левой боковой проекции определяют переднезадний диаметр сердца на месте наибольшей ширины сердца. Площадь сердца в передней проекции определяют следующим образом. Верхняя граница сердца не видна, ее надо провести, соединив дугообразной линией точку D с точкой G, нижнюю границу сердца определяют путем соединения дугообразной линией точки. Измеряют площадь сердца при помощи планиметра или переводят рентгенограмму на миллиметровую бумагу и высчитывают по ней число квадратных миллиметров. Рентгенологические методы определения объема сердца не нашли широкого применения в практике. Однако в настоящее время измерения объема сердца приобретают особое значение, так как в результате, например, операций на сердце могут наступать значительные изменения гемодинамики, ведущие к уменьшению размеров сердца. Объективным показателем этих изменений является количественная характеристика, получаемая методом измерения объема. Так, убедительные данные улучшения гемодинамики после митральной комиссуротомии получены с помощью этого метода в работе М. А. Иваницкой и И. И. Рушанова (1962).

Источник

Добавить комментарий