Площадь поверхности шарового сегмента
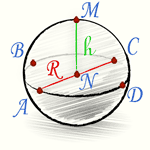
Часть шара, [шар, сфера] осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом. Основанием шарового сегмента называется круг ABCD. Высотой шарового сегмента называется отрезок NM, т.е. длина перпендикуляра, восстановленного из центра N основания до пересечения с поверхностью шара. Точка M называется вершиной шарового сегмента.
Площадь поверхности шарового сегмента равняется произведению его высоты на окружность большого круга шара.
[ S = 2 pi R h ]
(R – радиус большого круга шара, h=NM – высота шарового сегмента)
Формулы шара, сферы
Вычислить, найти площадь поверхности шарового сегмента по формуле (1)
Площадь поверхности шарового сегмента |
стр. 318 |
|---|
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности сегмента шара, а также разберем пример решения задачи для демонстрации их практического применения.
- Определение сегмента шара
-
Формулы для нахождения площади сегмента шара
- Площадь основания
- Площадь сферической поверхности
- Площадь полной поверхности
- Пример задачи
Определение сегмента шара
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.
- R – радиус шара;
- r – радиус основания сегмента;
- h – высота сегмента; это длина перпендикуляра от центра его основания (точка O2) до точки на поверхности шара.
Связь между радиусом основания сегмента, его высотой и радиусом шара:
Формулы для нахождения площади сегмента шара
Площадь основания
Основанием шарового сегмента является круг, площадь (S) которого находится по стандартной формуле (в расчетах число π округляется до 3,14):
Sосн. = πr 2
Примечание: если известен диаметр круга (d), чтобы найти радиус (r), нужно первое разделить на второе, то есть: r = d/2.
Площадь сферической поверхности
Чтобы найти площадь (S) сферической/внешней поверхности шарового сегмента, необходимо знать его высоту и радиус самого шара.
Sсфер. пов. = 2πRh
Площадь полной поверхности
Чтобы найти площадь (S) полной поверхности сегмента шара, необходимо сложить площади его основания и внешней поверхности.
Sполн. = Sосн. + Sсфер. пов. = π (2Rh + r 2)
Пример задачи
Дан шар радиусом 6 см. Найдите полную площадь шарового сегмента, если известно, что его высота равняется 2,4 см, а радиус основания – 4,7 см.
Решение
Воспользуемся формулами, приведенными выше, подставив в них известные по условиям задачи значения.
Sосн. = 3,14 ⋅ (4,7 см) 2 = 69,3626 см 2
Sсфер. пов. = 2 ⋅ 3,14 ⋅ 6 см⋅ 2,4 см = 90,432 см 2
Sполн. = Sосн. + Sсфер. пов. = 69,3626 см 2 + 90,432 см 2 = 159,7946 см 2
Площадь на сфере: сферы, шапочки, кольца
совместно с Арсением Акопяном
Площадь всей сферы, шапочки или кольца на сфере посчитать не так просто. Помогает сравнение сферы с «плоскими»
поверхностями — плоскостью, конусом и цилиндром.
Если плоскость касается сферы в полюсе, то площадь сферической шапочки и круга на плоскости, высекаемых «вспомогательной»
сферой с центром в полюсе, — одинакова. Если радиус вспомогательной сферы равен диаметру основной, то вспомогательная
полностью охватывает основную сферу. Эта картинка позволяет запомнить, что площадь сферы равна $4pi R^2$.
«Считывая» с глобуса информацию по приведённому алгоритму, можно построить равновеликую азимутальную картографическую проекцию
Земли. Такая проекция сохраняет площади всех областей. Разработал её математик и астроном Иоганн Ламберт — тот самый, который
доказал иррациональность числа $pi$. Заметный недостаток проекции — значительное искажение на общей карте Земли контуров крупных
областей, например, континентов.
Круг, касающийся сферы в полюсе, можно считать предельным случаем конуса, касающегося сферы.
Рассмотрим две вспомогательные концентрические сферы с центром в вершине конуса. И на сфере, и на конусе эти сферы высекают кольца.
Оказывается, что площади этих колец — на сфере и на конусе — равны.
Равенство остаётся верным для любого положения концентрических сфер. Рассмотренный случай равенства площадей шапочки на сфере
и соответствующего круга, касающегося сферы, получается из конического: радиус одной из концентрических сфер следует положить
нулю, а вершину конуса поместить в полюс сферы.
Если же вершину конуса «угнать» на бесконечность, то конус перейдёт в цилиндр, касающийся сферы по экватору. Концентрические
вспомогательные сферы перейдут в плоскости.
Площадь сферического кольца, вырезаемого двумя параллельными плоскостями, равна площади соответствующего цилиндрического кольца
(плоскости перпендикулярны оси цилиндра). Это приводит к интересному наблюдению: площадь кольца на глобусе зависит только
от расстояния между секущими плоскостями, но не зависит от близости кольца к экватору или полюсу. «Съедобное» толкование:
если круглый неочищенный апельсин нарезать на ломтики одинаковой толщины, то и площадь шкурки у всех кусков будет одинакова.
Сравнение площади кольца на сфере и кольца на цилиндре позволяет посчитать площадь всей сферы. Когда плоскости касаются полюсов
сферы расстояние между ними равно $2R$. А длина окружности цилиндра, касающегося сферы равна $2pi R$. Разворачивая цилиндр
в прямоугольник получаем $4pi R^2$.
Перенося информацию с глобуса на сферу с сохранением высоты получаем равновеликую цилиндрическую картографическую проекцию Земли.
Такая проекция, по рассмотренному выше свойству, сохраняет площади всех областей и тоже была разработана Ламбертом.
Утверждение про равенство площадей колец на сфере и на цилиндре называется леммой Архимеда и известно с давних времён. Утверждение
про площадь сферической шапочки и площадь круга тоже довольно известно. Удивительно, что связывающая эти два случая конструкция — сравнение
площадей колец на сфере и на конусе, заключённых между концентрическими сферами с центрами в вершине конуса — малоизвестна и, возможно,
была открыта только в XXI веке.
Другие этюды раздела «Площади и объёмы»
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
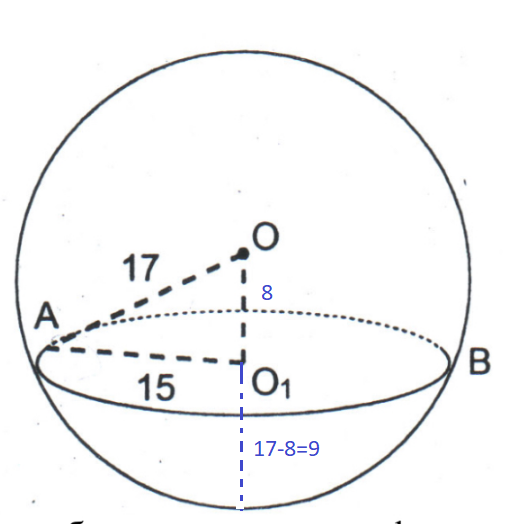
Задача 52439 Найти объем и площадь сферической части…
Условие
kkyjy
2020-06-15 05:56:33
Найти объем и площадь сферической части меньшего из шаровых сегментов.
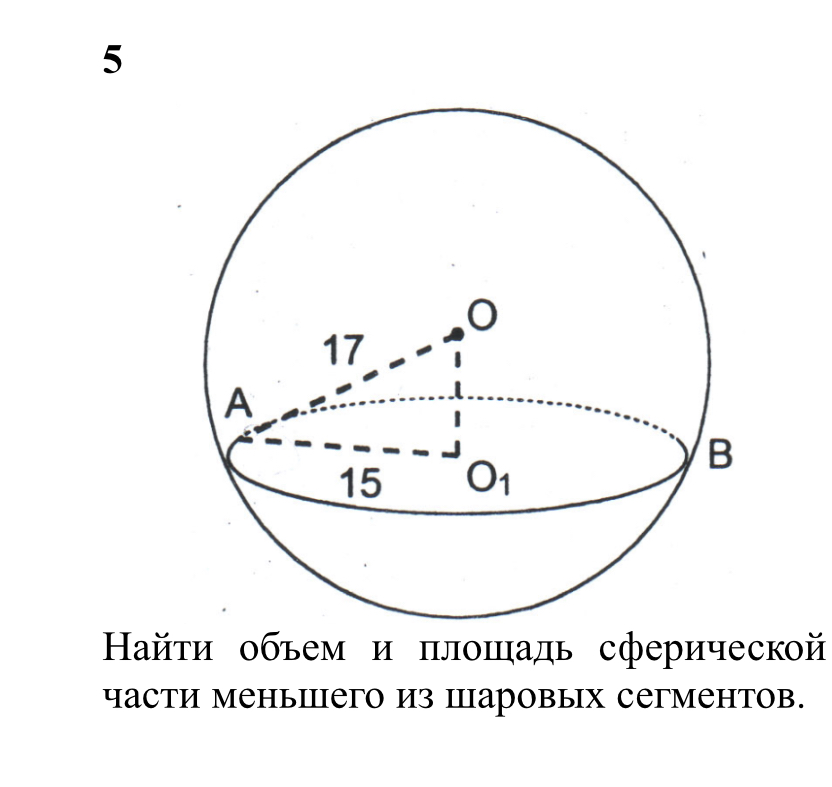
математика ВУЗ
4632
Все решения
sova
2020-06-15 14:39:00
По теореме Пифагора OO_(1)=sqrt(17^2-15^2)=8
h=17-8=9
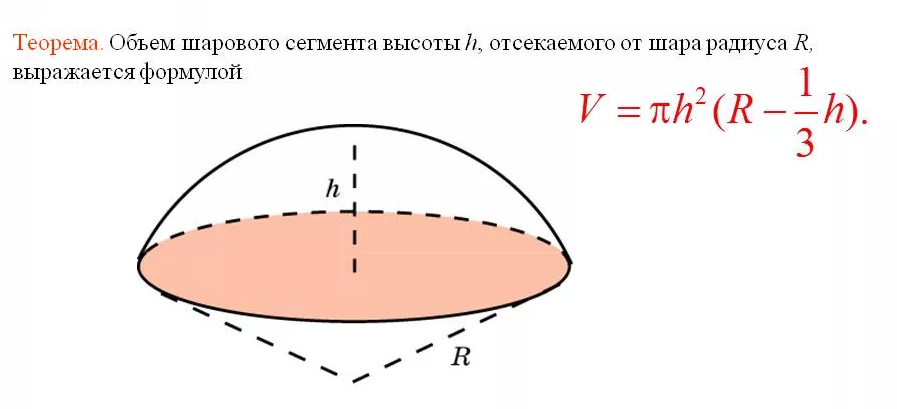
V=π*9^2*(17-(1/3)*9)=1134π
Написать комментарий
Категория
Стереометрия
Вычисление объемов, площадей поверх
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК

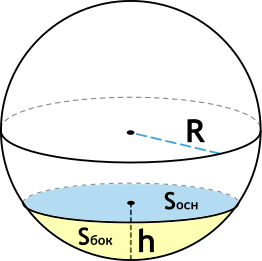
{S_{бок} = 2pi Rh} newline
{S_{осн} = pi h(2R-h)} newline
{S_{полн} = S_{бок}+S_{осн}}
С помощью приведенных на странице онлайн калькулятора и формулы вы можете рассчитать площадь поверхности шарового сегмента, которая состоит из площади боковой поверхности и площади основания. Введите радиус шара и высоту шарового слоя и получите результат.
Шарово́й сегмент — часть шара, отсеченная от него плоскостью.
Содержание:
- калькулятор площади поверхности шарового сегмента
- формула площади боковой поверхности шарового сегмента
- формула площади основания шарового сегмента
- формула площади полной поверхности шарового сегмента

Формула площади боковой поверхности шарового сегмента
{S_{бок} = 2pi Rh}
R – радиус шара
h – высота шарового сегмента
Формула площади основания шарового сегмента
{S_{осн} = pi h(2R-h)}
R – радиус шара
h – высота шарового сегмента
Формула полной поверхности шарового сегмента
{S_{осн} = S_{бок} + S_{осн}}
Sбок – площадь боковой поверхности шарового сегмента
Sосн – площадь основания шарового сегмента