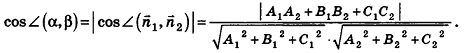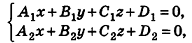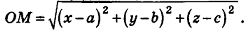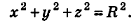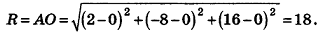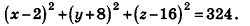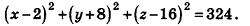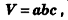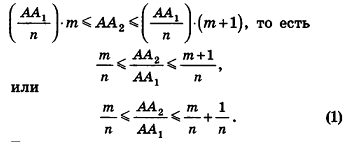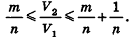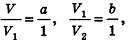В данной публикации мы рассмотрим, как найти радиус описанной около конуса сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.
- Нахождение радиуса сферы/шара
- Формулы площади и объема сферы/шара
Нахождение радиуса сферы/шара
Около любого конуса можно описать сферу (шар). Другими словами, в любую сферу можно вписать конус.
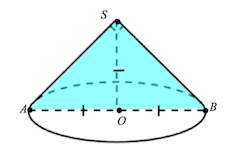
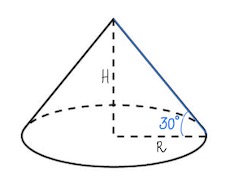
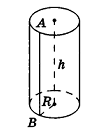
Чтобы найти радиус сферы (шара), описанной около конуса, чертим осевое сечение конуса. В итоге у нас получится равнобедренный треугольник (в нашем случае – ABC), вокруг которого описана окружность с радиусом r.
Радиус основания конуса (R) равен половине основания треугольника (AC), а образующие (l) – его боковые стороны (AB и BC).
Радиус окружности (r), описанной вокруг треугольника ABC, в том числе, является радиусом шара, описанного около конуса. Он находится по следующим формулам:
1. Через образующую и радиус основания конуса:
2. Через высоту и радиус основания конуса
Высота (h) конуса – это отрезок BE на рисунках выше.
Формулы площади и объема сферы/шара
Зная радиус (r) можно найти площадь поверхности (S) сферы и объем (V) шара, ограниченного этой сферой:
Примечание: π округленно равняется 3,14.
Нахождение радиуса/площади/объема описанной около конуса сферы (шара)
В данной публикации мы рассмотрим, как найти радиус описанной около конуса сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.
- Нахождение радиуса сферы/шара
- Формулы площади и объема сферы/шара
Нахождение радиуса сферы/шара
Около любого конуса можно описать сферу (шар). Другими словами, в любую сферу можно вписать конус.
Чтобы найти радиус сферы (шара), описанной около конуса, чертим осевое сечение конуса. В итоге у нас получится равнобедренный треугольник (в нашем случае – ABC), вокруг которого описана окружность с радиусом r.
Радиус основания конуса (R) равен половине основания треугольника (AC), а образующие ( l ) – его боковые стороны (AB и BC).
Радиус окружности (r), описанной вокруг треугольника ABC, в том числе, является радиусом шара, описанного около конуса. Он находится по следующим формулам:
1. Через образующую и радиус основания конуса:
2. Через высоту и радиус основания конуса
Высота (h) конуса – это отрезок BE на рисунках выше.
Формулы площади и объема сферы/шара
Зная радиус (r) можно найти площадь поверхности (S) сферы и объем (V) шара, ограниченного этой сферой:
геометрия — Найти радиус основания конуса [закрыт]
Угол равен 30 градусам, если я правильно понимаю (без такого добавления угловая мера «по умолчанию» считается радианной). Осевое сечение — равнобедренный треугольник. Основание равно $%2Rsinvarphi$% по теореме синусов, где $%varphi$% — угол при вершине. Отсюда всё сразу находится. Можно то же самое получить через половину центрального угла ($%r=Rsinvarphi$%, где $%r$% — половина длины основания треугольника, она же — радиус основания конуса).
05. Конус
Задача 1. Высота конуса равна , образующая равна Найдите его объем, деленный на .
Объем конуса вычисляется по формуле где – радиус основания, – высота конуса.
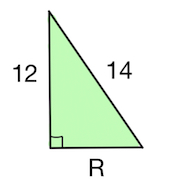
Задача 2. Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного Найдите его объем, деленный на .
В качестве высоты конуса выступает катет треугольника, равный В качестве радиуса основания конуса – второй катет треугольника, равны также
Задача 3. Высота конуса равна а диаметр основания – Найдите образующую конуса.
Найдем образующую конуса из прямоугольного треугольника по т. Пифагора.
При этом заметим, что
Задача 4. Найдите объем конуса, образующая которого равна и наклонена к плоскости основания под углом В ответе укажите
где – радиус основания конуса, – высота
Высота конуса как катет напротив угла в равен половине гипотенузы длиной , то есть равен
При этом по теореме Пифагора
Задача 5. Длина окружности основания конуса равна образующая равна Найдите площадь боковой поверхности конуса.
где – радиус основания конуса и образующая конуса.
А поскольку длина окружности основания конуса равна и равна по условию, то
Задача 6. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в раз?
Площадь боковой поверхности конуса зависит от двух величин – от и , так как
( – радиус, образующая конуса)
Радиус не изменяется, а образующая увеличивается в раз. Значит и площадь боковой поверхности конуса увеличится в раз.
Задача 7. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в раз?
Если высоту уменьшаем в раз, то и объем уменьшается в раз.
Задача 8. Во сколько раз увеличится объем конуса, если радиус его основания увеличится в раз, а высота останется прежней?
Увеличение радиуса основания в раз повлечет за собой увеличение объема конуса в то есть в раз.
Задача 9. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
( – радиус основания конуса, образующая конуса).
Прямоугольный треугольник, образованный высотой, образующей и радиусом основания таков, что катет, равный радиусу, вдвое меньше гипотенузы, значит угол между образующей конуса и плоскостью основания равен
Задача 10. Объем конуса равен Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Отсекаемый конус подобен исходному и – коэффициент подобия.
Как известно, объемы подобных тел находятся в отношении где – коэффициент подобия. Тогда объем отсекаемого конуса в раз (так как ) меньше объема исходного, то есть равен
Задача 11. Площадь полной поверхности конуса равна Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Малый отсеченный конус подобен исходному с коэффициентом подобия Площади поверхностей подобных тел находятся в отношении где – коэффициент подобия. Поэтому площади поверхностей будут отличаться в раза.
Значит, площадь полной поверхности отсеченного конуса есть
Задача 12. Найдите объем конуса, образующая которого равна и наклонена к плоскости основания под углом В ответе укажите .
где (так как напротив угла 30° лежит катет, вдвое меньший гипотенузы ())
Задача 13. Диаметр основания конуса равен а угол при вершине осевого сечения равен °. Вычислите объем конуса, деленный на .
Треугольник , образованный диаметром и соответствующими образующими, – прямоугольный и равнобедренный.
Середина гипотенузы является центром описанной окружности около треугольника . А значит . Поэтому, так как диаметр основания равен то
Задача 14. Площадь основания конуса равна , высота — Найдите площадь осевого сечения конуса.
Осевое сечение конуса – равнобедренный треугольник с основанием и высотой , проведенной к этому основанию.
Задача 15. Площадь основания конуса равна Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной и считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Плоскость, параллельная основанию, отсекает конус, подобный исходному и коэффициент подобия Площади оснований конусов отличаются тогда в раз.
Тогда площадь сечения конуса указанной плоскостью равна
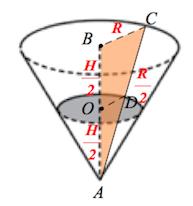
Задача 16. Найдите объем части конуса, изображенной на рисунке. В ответе укажите .
Часть конуса, изображенная на рисунке – это часть конуса с радиусом основания и высотой
Задача 17. Найдите объем части конуса, изображенной на рисунке. В ответе укажите .
Часть конуса, изображенная на рисунке – это часть конуса с радиусом основания и высотой
Задача 18. В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Отсеченный конус, образовавшийся при пересечении исходного конуса плоскостью параллельной основанию и пересекающей высоту конуса посередине, подобен исходному с коэффициентом подобия
Так как объемы подобных тел находятся в отношении , где – коэффициент подобия, то объем исходного конуса есть объемов отсеченного конуса ). Стало быть, на усеченный конус приходится объемов отсеченного (малого) конуса.
То есть объем усеченного конуса (а значит объем жидкости, что нужно долить) есть
Содержание:
Площади поверхностей геометрических тел:
Под площадью поверхности многогранника мы понимаем сумму площадей всех его граней. Как же определить площадь поверхности тела, не являющегося многогранником? На практике это делают так. Разбивают поверхность на такие части, которые уже мало отличаются от плоских. Тогда находят площади этих частей, как будто они являются плоскими. Сумма полученных площадей является приближенной площадью поверхности. Например, площадь крыши здания определяется как сумма площадей кусков листового металла. Еще лучше это видно на примере Земли. Приблизительно она имеет форму шара. Но площади небольших ее участков измеряют так, как будто эти участки являются плоскими. Более того, под площадью поверхности тела будем понимать предел площадей полных поверхностей описанных около него многогранников. При этом должно выполняться условие, при котором все точки поверхности этих многогранников становятся сколь угодно близкими к поверхности данного тела. Для конкретных тел вращения понятие описанного многогранника будет уточнено.
Понятие площади поверхности
Рассмотрим периметры
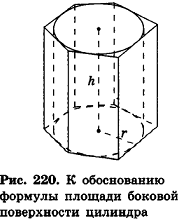
Применим данные соотношения к обоснованию формулы для площади боковой поверхности цилиндра.
При вычислении объема цилиндра были использованы правильные вписанные в него призмы. Найдем при помощи в чем-то аналогичных рассуждений площадь боковой поверхности цилиндра.
Опишем около данного цилиндра радиуса R и высоты h правильную n-угольную призму (рис. 220).
Площадь боковой поверхности призмы равна
где 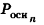
При неограниченном возрастании n получим:
так как периметры оснований призмы стремятся к длине окружности основания цилиндра, то есть к
Учитывая, что сумма площадей двух оснований призмы стремится к 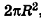
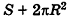
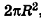
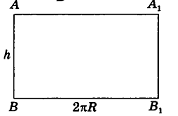
Итак, площадь боковой поверхности цилиндра вычисляется по формуле
где R — радиус цилиндра, h — его высота.
Заметим, что эта формула аналогична соответствующей формуле площади боковой поверхности прямой призмы
За площадь полной поверхности цилиндра принимается сумма площадей боковой поверхности и двух оснований:
Если боковую поверхность цилиндра радиуса R и высоты h разрезать по образующей АВ и развернуть на плоскость, то в результате получим прямоугольник 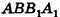
Очевидно, что сторона 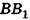
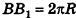
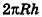
Пример:
Параллельно оси цилиндра на расстоянии d от нее проведена плоскость, отсекающая от основания дугу 
Решение:
Пусть дан цилиндр, в основаниях которого лежат равные круги с центрами 
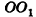
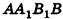
Пусть хорда АВ отсекает от окружности основания дугу 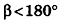
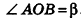
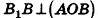
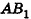
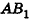
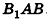
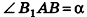
В равнобедренном треугольнике 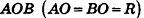
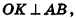
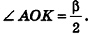
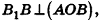
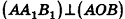
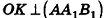
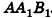
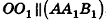
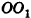
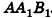
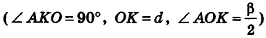
откуда 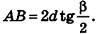
Итак,
В случае, когда
Аналогично предыдущему, и в этом случае получаем тот же результат для площади боковой поверхности.
Ответ:
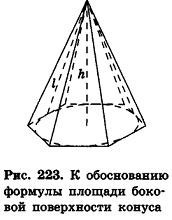
Площадь поверхности конуса и усеченного конуса
Связь между цилиндрами и призмами полностью аналогична связи между конусами и пирамидами. В частности, это касается формул для площадей их боковых поверхностей.
Опишем около данного конуса с радиусом основания R и образующей I правильную л-угольную пирамиду (рис. 223). Площадь ее боковой поверхности равна
где 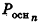
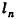
При неограниченном возрастании n получим:
так как периметры оснований пирамиды стремятся к длине окружности основания конуса, а апофемы 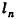
Учитывая, что площадь основания пирамиды стремится к 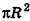
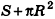
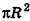
где R — радиус основания, I — образующая.
За площадь полной поверхности конуса принимается сумма площадей его основания и боковой поверхности:
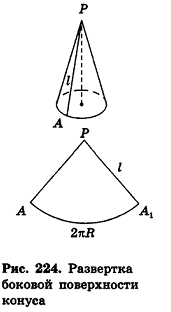
Если боковую поверхность конуса разрезать по образующей РА и развернуть на плоскость, то в результате получим круговой сектор 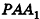
Очевидно, что радиус сектора развертки равен образующей конуса I, а длина дуги 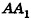
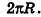
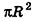
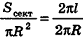
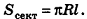
Учитывая формулу для площади боковой поверхности конуса, нетрудно найти площадь боковой поверхности усеченного конуса.
Рассмотрим усеченный конус, полученный при пересечении конуса с вершиной Р некоторой секущей плоскостью (рис. 225).
Пусть 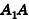
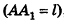
Из подобия треугольников
следует, что
Тогда получаем
Таким образом,
Итак, мы получили формулу для вычисления площади боковой поверхности усеченного конуса: 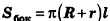
Отсюда ясно, что площадь полной поверхности усеченного конуса равна
Такой же результат можно было бы получить, если найти площадь развертки боковой поверхности усеченного конуса или использовать правильные усеченные пирамиды, описанные около него. Попробуйте дать соответствующие определения и провести необходимые рассуждения самостоятельно.
Связь между площадями поверхностей и объемами
При рассмотрении объемов и площадей поверхностей цилиндра и конуса мы видели, что существует тесная взаимосвязь между этими фигурами и призмами и пирамидами соответственно. Оказывается, что и сфера (шар), вписанная в многогранник, связана с величиной его объема.
Определение:
Сфера (шар) называется вписанной в выпуклый многогранник, если она касается каждой его грани.
При этом многогранник называется описанным около данной сферы (рис. 226).
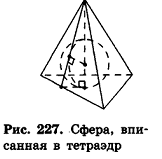
Рассмотрим, например, сферу, вписанную в тетраэдр (рис. 227).
Плоскости, содержащие грани тетраэдра, являются касательными к вписанной сфере, а точки касания лежат в гранях тетраэдра. Заметим, что по доказанному в п. 14.2 радиусы вписанной сферы, проведенные в точку касания с поверхностью многогранника, перпендикулярны плоскостям граней этого многогранника.
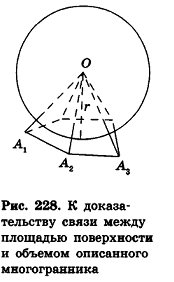
Для описанных многоугольников на плоскости было доказано, что их площадь равна произведению полупериметра на радиус вписанной окружности. Аналогичное свойство связывает объем описанного многогранника и площадь его поверхности.
Теорема (о связи площади поверхности и объема описанного многогранника)
Объем описанного многогранника вычисляется по формуле
где 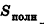
Доказательство:
Соединим центр вписанной сферы О со всеми вершинами многогранника 
где 
Теорема доказана.
Оказывается, что в любой тетраэдр можно вписать сферу, и только одну. Но не каждый выпуклый многогранник обладает этим свойством.
Рассматривают также сферы, описанные около многогранника.
Определение:
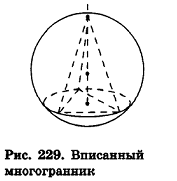
Сфера называется описанной около многогранника, если все его вершины лежат на сфере.
При этом многогранник называется вписанным в сферу (рис. 229).
Также считается, что соответствующий шар описан около многогранника.
Около любого тетраэдра можно описать единственную сферу, но не каждый многогранник обладает соответствующим свойством.
Площадь сферы
Применим полученную связь для объемов и площадей поверхностей описанных многогранников к выводу формулы площади сферы.
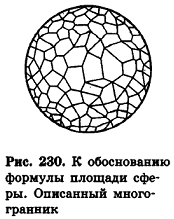
Опишем около сферы радиуса R выпуклый многогранник (рис. 230).
Пусть S’ — площадь полной поверхности данного многогранника, а любые две точки одной грани удалены друг от друга меньше чем на е. Тогда объем многогранника равен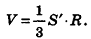
По неравенству треугольника 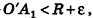
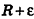
Итак, объем V данного многогранника больше объема шара радиуса R и меньше объема шара радиуса 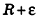
Отсюда получаем
Если неограниченно уменьшать размеры граней многогранника, то есть при е, стремящемся к нулю, левая и правая части последнего неравенства будут стремиться к 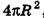
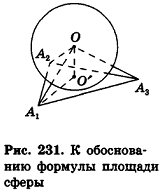
Итак, площадь сферы радиуса R вычисляется по формуле
Доказанная формула означает, что площадь сферы равна четырем площадям ее большого круга (рис. 232).
Исходя из аналогичных рассуждений, можно получить формулу для площади сферической части шарового сегмента с высотой Н:
Оказывается, что эта формула справедлива и для площади сферической поверхности шарового слоя (пояса):
где Н — высота слоя (пояса).
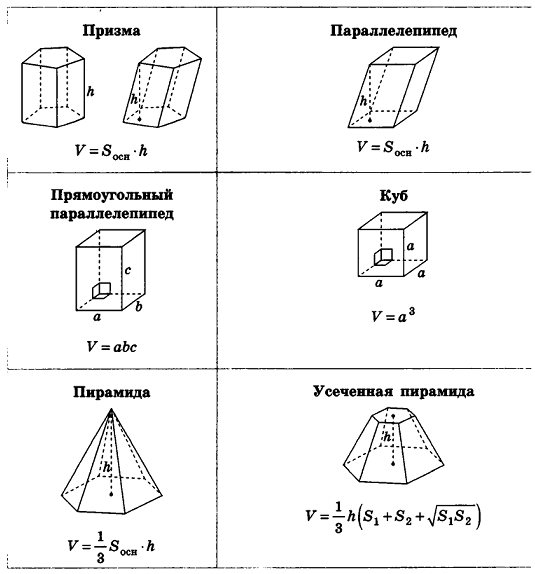
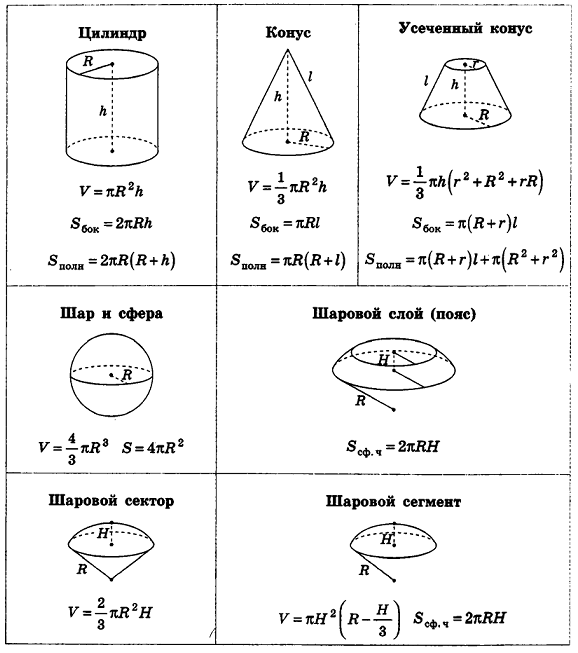
Справочный материал
Формулы объемов и площадей поверхностей геометрических тел
Историческая справка
Многие формулы для вычисления объемов многогранников были известны уже в Древнем Египте. В так называемом Московском папирусе, созданном около 4000 лет назад, вероятно, впервые в истории вычисляется объем усеченной пирамиды. Но четкие доказательства большинства формул для объемов появились позднее, в работах древнегреческих ученых.
Так, доказательства формул для объемов конуса и пирамиды связаны с именами Демокрита из Абдеры (ок. 460-370 гг. до н. э.) и Евдокса Книдского (ок. 408-355 гг. до н. э.). На основании их идей выдающийся математик и механик Архимед (287-212 гг. до н. э.) вычислил объем шара, нашел формулы для площадей поверхностей цилиндра, конуса, сферьГг
Дальнейшее развитие методы, предложенные Архимедом, получили благодаря трудам средневекового итальянского монаха и математика Бонавентуры Кавальери (1598-1647). В своей книге «Геометрия неделимых» он сформулировал принцип сравнения объемов, при котором используются площади сечений. Его рассуждения стали основой интегральных методов вычисления объемов, разработанных Исааком Ньютоном (1642 (1643)-1727) и Готфридом Вильгельмом фон Лейбницем (1646-1716). Во многих учебниках по геометрии объем пирамиды находится с помощью * чертовой лестницы» — варианта древнегреческого метода вычерпывания, предложенного французским математиком А. М. Лежандром (1752-1833).
На II Международном конгрессе математиков, который состоялся в 1900 году в Париже, Давид Гильберт сформулировал, в частности, такую проблему: верно ли, что любые два равновеликих многогранника являются равносоставленными? Уже через год отрицательный ответ на этот вопрос был обоснован учеником Гильберта Максом Деном (1878-1952). Другое доказательство этого факта предложил в 1903 году известный геометр В. Ф. Каган, который в начале XX века вел плодотворную научную и просветительскую деятельность в Одессе. В частности, из работ Дена и Кагана следует, что доказательство формулы объема пирамиды невозможно без применения пределов.
Весомый вклад в развитие теории площадей поверхностей внесли немецкие математики XIX века. Так, в 1890 году Карл Герман Аман-дус Шварц (1843-1921) построил пример последовательности многогранных поверхностей, вписанных в боковую поверхность цилиндра («сапог Шварца»). Уменьшение их граней не приводит к приближению суммы площадей этих граней к площади боковой поверхности цилиндра. Это стало толчком к созданию выдающимся немецким математиком и физиком Германом Минков-ским (1864-1909) современной теории площадей поверхностей, в которой последние связаны с объемом слоя около данной поверхности.
Учитывая огромный вклад Архимеда в развитие математики, в частности теории объемов и площадей поверхностей, именно его изобразили на Филдсовской медали — самой почетной в мире награде для молодых математиков. В 1990 году ею был награжден Владимир Дрин-фельд (род. в 1954 г.), который учился и некоторое время работал в Харькове. Вот так юные таланты, успешно изучающие геометрию в школе, становятся в дальнейшем всемирно известными учеными.
Уравнения фигур в пространстве
Напомним, что уравнением фигуры F на плоскости называется уравнение, которому удовлетворяют координаты любой точки фигуры F и не удовлетворяют координаты ни одной точки, не принадлежащей фигуре F. Так же определяют и уравнение фигуры в пространстве; но, в отличие от плоскости, где уравнение фигуры содержит две переменные х и у, в пространстве уравнение фигуры является уравнением с тремя переменными х, у и z.
Выведем уравнение плоскости, прямой и сферы в пространстве. Для получения уравнения плоскости рассмотрим в прямоугольной системе координат плоскость а (рис. 233) и определим свойство, с помощью которого можно описать принадлежность произвольной точки данной плоскости. Пусть ненулевой вектор 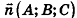
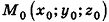
Так как 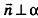
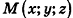
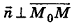
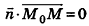
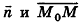
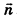
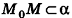
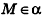
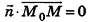
Теорема (уравнение плоскости в пространстве)
В прямоугольной системе координат уравнение плоскости имеет вид 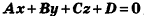
Доказательство:
Запишем в координатной форме векторное равенство 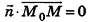
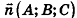
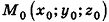
Следовательно,
После раскрытия скобок и приведения подобных членов это уравнение примет вид:
Обозначив числовое выражение в скобках через D, получим искомое уравнение, в котором числа А, В и С одновременно не равны нулю, так как 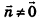
Покажем теперь, что любое уравнение вида Ах + Ву +Cz+D = 0 задает в пространстве плоскость. Действительно, пусть 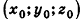
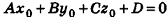
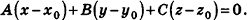
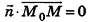
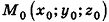
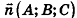
Обратим внимание на то, что в доказательстве теоремы приведен способ составления уравнения плоскости по данным координатам произвольной точки плоскости и вектора нормали.
Пример:
Напишите уравнение плоскости, которая перпендикулярна отрезку MN и проходит через его середину, если М{-1;2;3), N(5;-4;-1).
Решение:
Найдем координаты точки О — середины отрезка MN:
Значит, О (2; -1; l). Так как данная плоскость перпендикулярна отрезку MN, то вектор 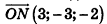
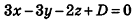
И наконец, так как данная плоскость проходит через точку О(2;-l;l), то, подставив координаты этой точки в уравнение, получим:
Таким образом, уравнение 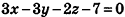
Ответ:
Заметим, что правильным ответом в данной задаче является также любое уравнение, полученное из приведенного умножением обеих частей на число, отличное от нуля.
Значения коэффициентов А, В, С и D в уравнении плоскости определяют особенности расположения плоскости в системе координат. В частности:
- если
, уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);
- если один из коэффициентов А, В и С равен нулю, a
, плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали
перпендикулярен оси Ох, а плоскость By + Cz + D = Q параллельна оси Ох (рис. 234, б)
- если два из коэффициентов А, В и С равны нулю, а
, плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали
перпендикулярен плоскости Оху, а плоскость Cz+D = 0 параллельна плоскости Оху (рис. 234, в);
- если два из коэффициентов А, В и С равны нулю и D = 0, плоскость совпадает с одной из координатных плоскостей: например, при условиях
и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
Предлагаем вам самостоятельно составить полную таблицу частных случаев расположения плоскости Ax + By+Cz+D = 0 в прямоугольной системе координат в зависимости от значений коэффициентов А, В, С и D.
Пример: (о расстоянии от точки до плоскости)
Расстояние от точки 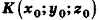
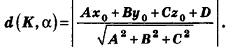
Решение:
Если 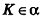
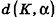
Если 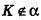
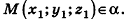
Тогда 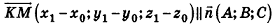
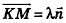
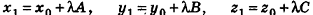
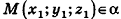
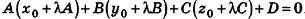
Таким образом,
Рассмотрим теперь возможность описания прямой в пространстве с помощью уравнений.
Пусть в пространстве дана прямая k (рис. 235). Выберем ненулевой вектор 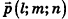
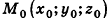
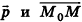
Представим это векторное равенство в координатной форме. Если ни одна из координат направляющего вектора не равна нулю, из данного равенства можно выразить t и приравнять полученные результаты:
Эти равенства называют каноническими уравнениями прямой в пространстве.
Пример:
Напишите уравнение прямой, проходящей через точки А(1;-3;2) и В(-l;0;l).
Решение:
Так как точки А и В принадлежат данной прямой, то 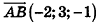
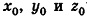
Ответ:
Заметим, что ответ в этой задаче может иметь и другой вид: так, в числителях дробей можно использовать координаты точки В, а как направляющий вектор рассматривать любой ненулевой вектор, коллинеарный 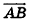
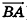
Вообще, если прямая в пространстве задана двумя точками 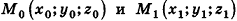
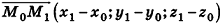
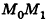
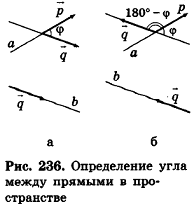
С помощью уравнений удобно исследовать взаимное расположение прямых и плоскостей в пространстве. Рассмотрим прямые 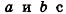
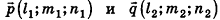
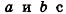
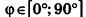
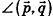
Так как cos(l80°-ф) = -coscp, имеем 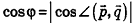
Отсюда, в частности, следует необходимое и достаточное условие перпендикулярности прямых 
Кроме того, прямые 
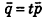
Проанализируем теперь отдельные случаи взаимного расположения двух плоскостей в пространстве. Очевидно, что если 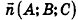
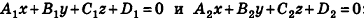
- совпадают, если существует число t такое, что
, или, если числа
ненулевые
- параллельны, если существует число t такое, что
, или, если координаты
ненулевые,
(на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где
).
В остальных случаях данные плоскости 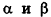
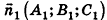
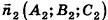
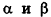
В частности, необходимое и достаточное условие перпендикулярности плоскостей 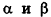
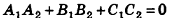
Заметим также, что прямая в пространстве может быть описана как линия пересечения двух плоскостей, то есть системой уравнений
где векторы 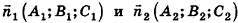
Пример:
Напишите уравнение плоскости, которая проходит через точку М(4;2;3) и параллельна плоскости x-y + 2z-S = 0.
Решение:
Так как искомая плоскость параллельна данной, то вектор нормали к данной плоскости 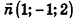
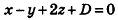
Ответ: x-y+2z-8 = 0.
Аналогично уравнению окружности на плоскости, в пространственной декартовой системе координат можно вывести уравнение сферы с заданным центром и радиусом.
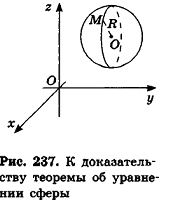
Теорема (уравнение сферы)
В прямоугольной системе координат уравнение сферы радиуса R с центром в точке 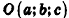
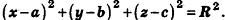
Пусть 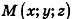
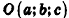
Так как OM=R, то есть ОМ2 = R2, то координаты точки М удовлетворяют уравнению 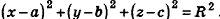
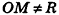
Следствие
Сфера радиуса R с центром в начале координат задается уравнением вида
Заметим, что фигуры в пространстве, как и на плоскости, могут задаваться не только уравнениями, но и неравенствами. Например, шар радиуса R с центром в точке 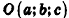
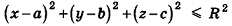
Пример:
Напишите уравнение сферы с центром А (2;-8; 16), которая проходит через начало координат.
Решение:
Так как данная сфера проходит через точку 0(0;0;0), то отрезок АО является ее радиусом. Значит,
Таким образом, искомое уравнение имеет вид:
Ответ:
Доказательство формулы объема прямоугольного параллелепипеда
Теорема (формула объема прямоугольного параллелепипеда)
Объем прямоугольного параллелепипеда равен произведению трех его измерений:
где 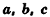
Доказательство:
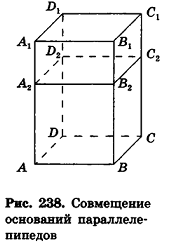
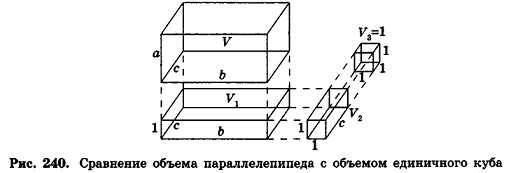
Докажем сначала, что объемы двух прямоугольных параллелепипедов с равными основаниями относятся как длины их высот.
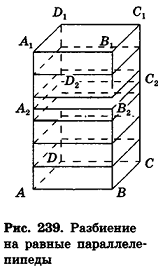
Пусть 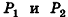
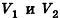
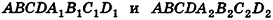
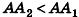
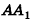
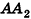
проведем через точки деления параллельные основанию ABCD (рис. 239). Они разобьют параллелепипед 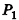
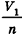
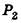
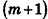
Таким образом, 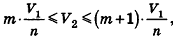
Сравнивая выражения (1) и (2), видим, что оба отношения 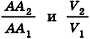
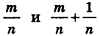
Допустим, что это не так, то есть 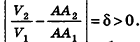
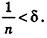
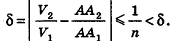
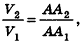
Рассмотрим теперь прямоугольные параллелепипеды с измерениями 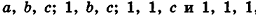
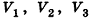
По аксиоме объема V3 =1. По доказанному 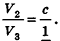
Теорема доказана.
* Выберем 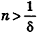
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии
- Многоугольник
- Площадь многоугольника
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Площади фигур в геометрии
Проверяемые элементы содержания и виды деятельности: владение понятиями о стереометрических фигурах; знание их свойств; знание формул для вычисления площадей поверхностей и объемов тел; умение применять эти знания при решении задач.
Ориентировочное время выполнения учащимися: 10—15 минут.
Типы заданий:
• Элементы, площадь поверхности, объем стереометрических фигур.
Особенности экзаменационных заданий по стереометрии
Задания этого вида представляют собой стереометрические задания на установление взаимосвязи между основными элементами многогранников и круглых тел, а также на использование формул для вычисления их площадей поверхностей и объемов. Вычислительной трудности задания не представляют; решение, как правило, сводится к использованию одной-двух формул. Соответствующие формулы нужно знать наизусть.
Куб
Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Куб является частный случаем параллелепипеда и призмы, поэтому для него выполнены все их свойства. Кроме того, если а — длина ребра куба, — диагональ основания,
— диагональ куба,
— площадь полной поверхности, а V — объем куба, то справедливы формулы:
Призма. Прямоугольный параллелепипед
Призмой (n-угольной призмой) называется многогранник, две грани которого — равные n-угольники, лежащие в параллельных плоскостях, а остальные n граней — параллелограммы.
Правильной призмой называется прямая призма, основание которой — правильный многоугольник.
Прямая призма
Прямой призмой называется призма, боковое ребро которой перпендикулярно плоскости основания. Высота прямой призмы равна ее боковому ребру, а все боковые грани прямой призмы — прямоугольники.
Соотношения для прямой призмы
Пусть H — высота прямой призмы, AA1 — боковое ребро, — периметр основания,
— площадь основания,
— площадь боковой поверхности,
— площадь полной поверхности, V — объем прямой призмы. Тогда имеют место следующие соотношения:
Особенности правильной шестиугольной призмы
В основании правильной шестиугольной призмы лежит правильный шестиугольник. Напомним его свойства.
— Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
— Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.
— Меньшая диагональ правильного шестиугольника в раз больше его стороны.
— Угол между сторонами правильного шестиугольника равен 120°.
— Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.
— Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.
Пирамида
Пусть вне плоскости многоугольника задана точка P. Тогда фигура, образованная треугольниками
,
и многоугольником
вместе с их внутренними областями называется пирамидой (n-угольной пирамидой).
Пирамида называется правильной, если ее основание — правильный многоугольник, а основание ее высоты — центр этого многоугольника.
Соотношения для правильной пирамиды
Пусть H — высота правильной пирамиды, h — ее апофема, — периметр основания пирамиды,
— площадь основания,
— площадь боковой поверхности,
— площадь полной поверхности, V — объем правильной пирамиды. Тогда имеют место следующие соотношения:
Сечения
Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырехугольники (рис. 1). Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники (рис. 2).
Теоремы, используемые при построении сечений
Теорема 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Поэтому секущая плоскость пересекает плоскости параллельных граней по параллельным прямым.
Теорема 2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Теорема 3. Если прямая l параллельна какой либо прямой m, проведённой в плоскости то она параллельна и самой плоскости
Теорема 4. Если прямая, лежащая в плоскости сечения, не параллельна плоскости некоторой грани, то она пересекается со своей проекцией на эту грань.
Алгоритм построения сечений
Для построения сечений рекомендуем пользоваться следующим алгоритмом.
1. Если две точки секущей плоскости лежат в плоскости одной грани, то проводим через них прямую. Часть прямой, лежащая в плоскости грани — сторона сечения.
2. Если прямая a является общей прямой секущей плоскости и плоскости какой-либо грани, то находим точки пересечения прямой a с прямыми, содержащими ребра этой грани. Полученные точки — новые точки секущей плоскости, лежащие в плоскостях граней.
3. Если никакие две из данных точек не лежат в плоскости одной грани, то строим вспомогательное сечение, содержащее любые две данные точки, а затем выполняем шаги 1, 2.
Для контроля правильности построенного сечения, проверяйте, что:
— все вершины сечения лежат на рёбрах многогранника;
— все стороны сечения лежат в гранях многогранника;
— в каждой грани многогранника лежит не более одной стороны сечения.
Цилиндр
Цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону.
Соотношения для цилиндра
Пусть h — высота цилиндра, r — радиус основания, Sбок — площадь боковой поверхности, Sполн — площадь полной поверхности, V — объем цилиндра. Тогда имеют место следующие соотношения:
Конус
Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет.
Соотношения для конуса
Пусть h — высота конуса, r — радиус основания, l — образующая, Sбок — площадь боковой поверхности, Sполн — площадь полной поверхности, V — объем конуса. Тогда имеют место следующие соотношения:
Сфера и шар
Шаром называется фигура, полученная при вращении полукруга вокруг оси, содержащей его диаметр. Сферой называется поверхность шара. Пусть R — радиус шара, S — площадь сферы, V — объем шара. Тогда имеют место следующие соотношения:
Комбинации круглых тел. Вписанные сферы
Сфера называется вписанной в цилиндр, если она касается обоих оснований цилиндра и каждой его образующей.
Сфера называется вписанной в конус, если она касается основания конуса и каждой его образующей.
Сфера называется вписанной в усечённый конус, если она касается обоих оснований конуса и всех его образующих.
Теорема 1: В прямой круговой цилиндр можно вписать сферу тогда и только тогда, когда его высота равна диаметру основания. Причём центр сферы есть середина оси цилиндра.
Теорема 2: В любой прямой круговой конус можно вписать сферу. Причём центр сферы есть точка пересечения оси конуса с биссектрисой угла наклона образующей конуса к плоскости его основания.
Теорема 3. В усечённый конус можно вписать сферу тогда и только тогда, когда он прямой круговой, и длина его образующей равна сумме длин радиусов оснований. Причём центр сферы есть середина оси усечённого конуса.
Комбинации круглых тел. Описанные сферы
Сфера называется описанной около цилиндра, если окружности его оснований лежат на сфере.
Сфера называется описанной около конуса, если вершина конуса и его основание лежат на сфере.
Теорема 1: около цилиндра можно описать сферу тогда и только тогда, когда он прямой круговой. Причём центр сферы есть середина оси цилиндра.
Теорема 2: около конуса можно описать сферу тогда и только тогда, когда он круговой. Причём центр сферы есть точка пересечения прямой, перпендикулярной к плоскости основания и проходящей через центр его, и плоскости, перпендикулярной какой-либо его образующей конуса и проходящей середину этой образующей.
Следствие: сферу можно описать около любого прямого кругового конуса. В этом случае, центр сферы — точка пересечения прямой, содержащей высоту конуса с плоскостью, перпендикулярной какой-либо из его образующих и проходящей через ее середину.
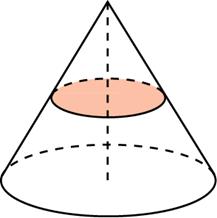
Комбинации конуса и цилиндра
Цилиндр называется вписанным в конус, если одно его основание лежит на основании конуса, а второе совпадает с сечением конуса плоскостью, параллельной основанию. Конус в этом случае называется описанным вокруг цилиндра.
Цилиндр называется описанным вокруг конуса, если центр одного из оснований цилиндра является вершиной вершина конуса, а противоположное основание цилиндра совпадает с основанием конуса. Конус в этом случае называется вписанным в цилиндр.
Комбинации многогранников и круглых тел. Описанные сферы
Сфера называется описанной около многогранника, если все его вершины лежат на этой сфере. Многогранник называется в этом случае вписанным в сферу.
Возможность описать сферу около многогранника означает существование точки (центра сферы), равноудалённой ото всех вершин многогранника.
Теорема 1: если из центра описанной около многогранника сферы опустить перпендикуляр на какое-либо из его рёбер, то основание этого перпендикуляра разделит ребро на две равные части.
Теорема 2: если из центра описанной около многогранника сферы опустить перпендикуляр на какую-либо из его граней, то основание этого перпендикуляра попадёт в центр круга, описанного около соответствующей грани.
Теорема 3: если около многогранника описана сфера, то её центр лежит на пересечении перпендикуляров к каждой грани пирамиды, проведённых через центр окружности, описанной около соответствующей грани.
Теорема 4: если около многогранника описана сфера, то её центр является точкой пересечений всех плоскостей, проведённых через середины рёбер пирамиды перпендикулярно к этим рёбрам.
Комбинации многогранников и круглых тел. Вписанные сферы
Сфера называется вписанной в многогранник, если все его грани касаются этой сферы. Многогранник называется в этом случае описанным около сферы.
Теорема: если в многогранник с площадью поверхности S и объёмом V вписан шар радиуса r, то справедливо соотношение:
Комбинации конуса, цилиндра и многогранников
В условиях задач встречаются также следующие понятия, не входящие в школьные учебники, которые уточняются непосредственно в условиях задач. Приведем наиболее употребительные из них.
Цилиндр вписан в призму: основания цилиндра вписаны в основания призмы.
Цилиндр описан вокруг призмы: основания цилиндра описаны вокруг оснований призмы.
Цилиндр вписан в пирамиду: одно из основание цилиндра вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание цилиндра принадлежит основанию пирамиды.
Цилиндр описан вокруг пирамиды: вершина пирамиды принадлежит одному из оснований цилиндра, а другое его основание описано вокруг основания пирамиды.
Конус вписан в призму: основание конуса вписано в основание призмы, а вершина конуса принадлежит противоположному основанию призмы.
Конус описан вокруг призмы: одно из оснований призмы вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание призмы вписано в основание конуса.
Конус вписан в пирамиду: их вершины совпадают, а основание конуса вписано в основание пирамиды. Вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой.
Конус описан вокруг пирамиды: их вершины совпадают, а основание конуса описано вокруг основания пирамиды.
Пирамида, вписанная в конус
Пирамида называется вписанной в конус, если ее основание вписано в основание конуса, а вершина совпадает с вершиной конуса. При этом конус называется описанным около пирамиды.
Около пирамиды можно описать конус тогда и только тогда, когда около ее основания можно описать окружность.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Упражнение 1
Найдите сторону основания правильной треугольной пирамиды, вписанной в конус, радиус основания которого равен 1.
Ответ:
Упражнение 2
Найдите сторону основания правильной четырехугольной пирамиды, вписанной в конус, радиус основания которого равен 1.
Ответ:
Упражнение 3
Найдите сторону основания правильной шестиугольной пирамиды, вписанной в конус, радиус основания которого равен 1.
Ответ: 1.
Пирамида, описанная около конуса
Пирамида называется описанной около конуса, если ее основание описано около основания конуса, а вершина совпадает с вершиной конуса. При этом конус называется вписанным в пирамиду.
В пирамиду можно вписать конус тогда и только тогда, когда в ее основание можно вписать окружность.
Упражнение 1
Найдите сторону основания правильной треугольной пирамиды, описанной около конуса, радиус основания которого равен 1.
Ответ:
Упражнение 2
Найдите сторону основания правильной четырехугольной пирамиды, описанной около конуса, радиус основания которого равен 1.
Ответ: 2.
Упражнение 3
Найдите сторону основания правильной шестиугольной пирамиды, описанной около конуса, радиус основания которого равен 1.
Ответ:
Сфера, вписанная в конус
Сфера называется вписанной в конус, если она касается его основания и боковой поверхности (касается каждой образующей). При этом конус называется описанным около сферы.
В любой конус (прямой, круговой) можно вписать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, вписанной в треугольник, являющийся осевым сечением конуса.
Напомним, что радиус r окружности, вписанный в треугольник, находится по формуле
где S – площадь, p – полупериметр треугольника.
Упражнение 1
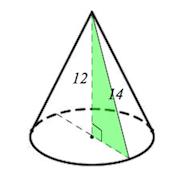
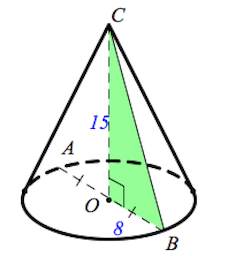
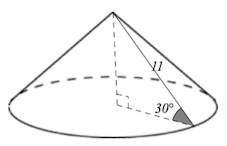
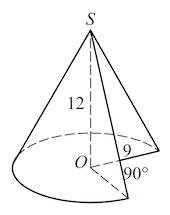
В конус, радиус основания которого равен 1, а образующая равна 2, вписана сфера. Найдите ее радиус.
Решение. Треугольник SAB равносторонний. Высота SH равна Площадь S равна Полупериметр p равен 3. По формуле r = S/p получаем
Упражнение 2
В конус, радиус основания которого равен 2, вписана сфера радиуса 1. Найдите высоту конуса.
Решение. Обозначим h высоту SH конуса . Из формулы r = S/p имеем:
где r = 1, a = FG = 4, p =
Решая уравнение
находим
Упражнение 3
Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45 о . Найдите радиус вписанной сферы.
Решение. Высота SH конуса равна 1. Образующая .
Полупериметр p равен
По формуле r = S/p , имеем
Ответ:
Упражнение 4
Высота конуса равна 8, образующая 10. Найдите радиус вписанной сферы.
Решение. Радиус основания конуса равен 6. Площадь треугольника SFG равна 48, полупериметр 16. По формуле r = S/p имеем r = 3.
Ответ: r = 3.
Упражнение 5
Можно ли вписать сферу в наклонный конус?
Ответ: Нет.
Сфера, вписанная в усеченный конус
Сфера называется вписанной в усеченный конус, если она касается его основани й и боковой поверхности (касается каждой образующей). При этом усеченный конус называется описанным около сферы.
В усеченный конус можно вписать сферу, если в его осевое сечение можно вписать окружность. Радиус этой окружности будет равен радиусу вписанной сферы.
Упражнение 1
В усеченный конус, радиусы оснований которого равны 2 и 1, вписана сфера. Найдите радиус сферы и высоту усеченного конуса.
Решение. Имеем: A 1 B = A 1 O 1 = 2, A 2 B = A 2 O 2 = 1. Следовательно, A 1 A 2 = 3 , A 1 C = 1.
Таким образом,
Упражнение 2
В усеченный конус, радиус одного основания которого равен 2, вписана сфера радиуса 1. Найдите радиус второго основания.
Решение. Пусть A 1 O 1 = 2. Обозначим r = A 2 O 2 . Имеем: A 1 A 2 = 2+ r , A 1 C = 2 – r . По теореме Пифагора, имеет место равенство из которого следует, что выполняется равенство Решая полученное уравнение относительно r , находим
Упражнение 3
В усеченном конусе радиус большего основания равен 2, образующая наклонена к плоскости основания под углом 60 о . Найдите радиус вписанной сферы.
Решение. Заметим, что осевым сечением конуса, из которого получен усеченный конус, является равносторонний треугольник со стороной 2. Радиус r сферы, вписанной в усеченный конус, равен радиусу окружности, вписанной в этот равносторонний треугольник, т.е.
Упражнение 4
Образующая усеченного конуса равна 2, площадь осевого сечения 3. Найдите радиус вписанной сферы.
Решение. Воспользуемся формулой r = S/p , где S – площадь осевого сечения, p – полупериметр. В нашем случае S = 3 . Для нахождения полупериметра напомним, что для четырехугольника, описанного около окружности, суммы противоположных сторон равны. Значит, полупериметр равен удвоенной образующей цилиндра, т.е. p = 4. Следовательно, r = ¾.
Ответ:
Упражнение 5
Можно ли вписать сферу в усеченный наклонный конус.
Ответ: Нет.
Сфера, описанная около конуса
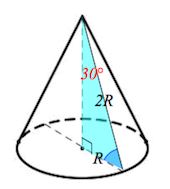
Сфера называется описанной около конуса, если вершина и окружность основания конуса лежат на сфере. При этом конус называется вписанным в сферу .
Около любого конуса (прямого, кругового) можно описать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, описанной около треугольника, являющимся осевым сечением конуса.
Напомним, что радиус R окружности, описанной около треугольника, находится по формуле
где S – площадь, a , b , c – стороны треугольника.
Упражнение 1
Около конуса, радиус основания которого равен 1, а образующая равна 2, описана сфера. Найдите ее радиус.
Решение. Треугольник SAB равносторонний со стороной 2. Высота SH равна Площадь S равна По формуле R = abc /4 S получаем
Упражнение 2
Около конуса, радиус основания которого равен 4, описана сфера радиуса 5. Найдите высоту h конуса.
Решение. Имеем, OB = 5 , HB = 4. Следовательно, OH = 3. Учитывая, что SO = OB = 5, получаем h = 8.
Ответ: h = 8.
Упражнение 3
Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45 о . Найдите радиус описанной сферы.
Решение. Треугольник SAB – прямоугольный, равнобедренный. Следовательно, радиус R описанной сферы равен радиусу основания цилиндра, т.е. R = 1.
Ответ: R = 1.
Упражнение 4
Высота конуса равна 8, образующая 10. Найдите радиус описанной сферы.
Решение. В треугольнике SAB имеем: SA = SB = 10, SH = 8. По теореме Пифагора, AH = 6 и, следовательно, S = 48. Используя формулу R = abc /4 S , получаем
Упражнение 5
Можно ли описать сферу около наклонного конуса?
Ответ: Да.
Сфера, описанная около усеченного конуса
С фера называется описанной около усеченного конуса, если окружност и основани й усеченного конуса лежат на сфере. При этом усеченный к онус называется в писанным в сферу.
Около усеченного конуса можно описать сферу, если около его осевого сечения можно описать окружность. Радиус этой окружности будет равен радиусу описанной сферы.
Упражнение 1
Около усеченного конуса, радиусы оснований которого равны 2 и 1, а образующая равна 2, описана сфера. Найдите ее радиус.
Решение. Заметим, что A 1 O 1 B 2 O 2 и O 1 B 1 B 2 A 2 – ромбы. Треугольники A 1 O 1 A 2 , O 1 A 2 B 2 , O 1 B 1 B 2 – равносторонние и, значит, A 1 B 1 –диаметр. Следовательно, R = 2.
Ответ: R = 2,
Упражнение 2
Радиус меньшего основания усеченного конуса равен 1, образующая равна 2 и составляет угол 45 о с плоскостью другого основания. Найдите радиус описанной сферы.
Решение. Имеем A 2 O 2 = 1, A 1 A 2 = 2, O 1 O 2 = , OO 1 = O 1 C = 1. Следовательно, OO 2 = 1 + и, значит,
Упражнение 3
Радиус одного основания усеченного конуса равен 4, высота 7, радиус описанной сферы 5. Найдите радиус второго основания усеченного конуса.
Решение. Имеем OO 1 = 3 , OO 2 = 4 и, следовательно, O 2 A 2 = 3.
Ответ: 3.
Упражнение 4
Найдите радиус сферы, описанной около усеченного конуса, радиусы оснований которого равны 2 и 4, а высота равна 5.
Решение. Обозначим R радиус описанной сферы. Тогда
Учитывая, что O 1 O 2 = 6, имеем равенство
Решая его относительно R , находим
Упражнение 5
Можно ли описать сферу около усеченного наклонного конуса.
Ответ: Нет.





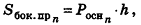
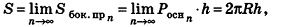
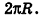
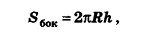
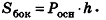
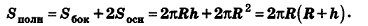

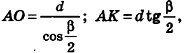
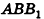
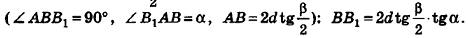
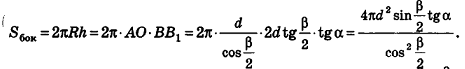
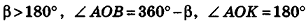
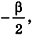
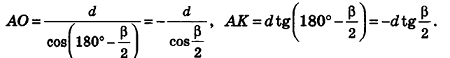
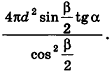
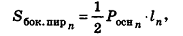
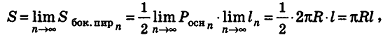
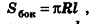
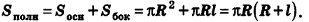
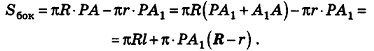
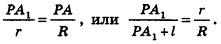
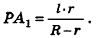
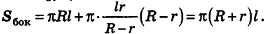
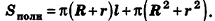
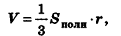
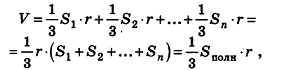
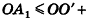
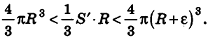
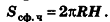
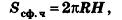






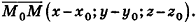
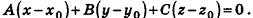
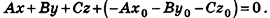
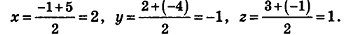
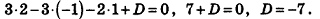
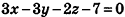
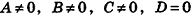 , уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);
, уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);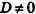 , плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали
, плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали 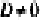 , плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали
, плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали 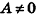 и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).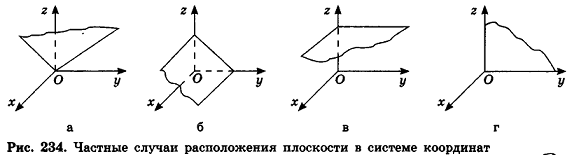
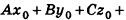
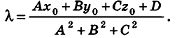
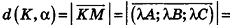
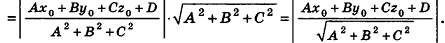
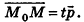
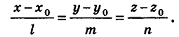
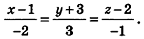
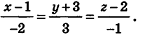
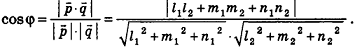
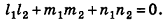
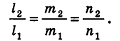
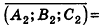
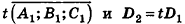 , или, если числа
, или, если числа 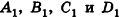 ненулевые
ненулевые 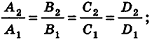
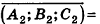
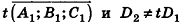 , или, если координаты
, или, если координаты 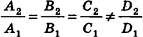 (на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где
(на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где 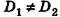 ).
).