Как найти площадь сферы вписанной в призму

Шар вписанный в призму, касается каждой ее грани. Диаметр вписанного шара равен высоте призмы, а также равен диаметру окружности, вписанной в основание призмы.

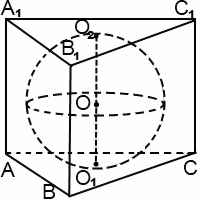
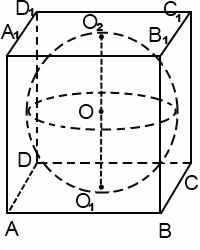
Центр шара лежит на середине высоты призмы, проведенной через центр вписанной в основание окружности. Если в основание призмы нельзя вписать окружность либо высота призмы не равна диаметру вписанной в основание окружности, то в такую призму шар вписать нельзя.

Если призма правильная, центр вписанного в нее шара является точкой пересечения бисекторных плоскостей призмы.

При решении задач на шар,вписанный в призму, можно рассмотреть сечение комбинации тел плоскостью, параллельной основаниям. Она представляет собой многоугольник, равный многоугольнику основания, с вписанной в него окружностью, радиус которой равен радиусу шара. Далее используем формулы, связывающие радиус вписанной окружности со сторонами основания, а также то, что центр вписанной в многоугольник окружности является точкой пересечения его биссектрис.

Выразим объем призмы через радиус вписанного шара — R. Объем призмы равен

Площадь основания ищем по формуле S=pr, где p — полупериметр основания, r — радиус вписанной в него окружности. Поскольку в нашем случае r=R и высота призмы H=2R, то

Но 2p=P — периметру основания. Окончательно имеем

Выразим площадь полной поверхности прямой призмы через радиус вписанного в нее шара. Площадь полной поверхности прямой призмы равна сумме площадей оснований и боковой поверхности:

Боковая поверхность

Отсюда

Таким образом, пришли к формуле

Ну обе эти задачи на ортогональное проектирование всего на основание. В первой,проектируя все на любую из граней, получишь, что сфера проектируется в окружность, а параллелепипед в прямоугольник, получишь, что у Тебя окружность вписана в прямоугольник, следовательно, очевидно, что он квадрат. И так для любой из граней, следовательно параллелепипед Твой– куб, с гранями 2Rх2R, следовательно площадьповерхности равна 6*4*R^2=24R^2.

Во второй задаче нужно спроектировать все на нижнее основание, тогда ты получишь, что призма проектируется в треугольник, а сфера —во вписанную в него окружность(т. к. призма прямоугольная, и проектирование ортогональное). Ну ты уж сам посчитай, пожалуйста, радиус окружности вписанной в прямоугольный треугольник с гипотенузой 25 и высотой 12. Это и есть радиус вписанной в призму сферы, ну уж площадь поверхности сферы через радиус, я думаю Ты посчитаешь… Удачи, если, что не ясно, то пиши на мыло.

Подпишись на наш канал в телеграм. Там мы даём ещё больше полезной информации для школьников!

Слайд 1

Сфера, вписанная в многогранник Богаевская Галина Николаевна учитель математики ГБОУ гимназии 446 Санкт-Петербурга

Слайд 2

Сфера, вписанная в многогранник Определение Многогранник называется описанным около сферы (а сфера вписанной в многогранник ), если все грани многогранника касаются этой сферы. Следствие Центр вписанной сферы есть точка, равноудаленная от всех граней многогранника.

Слайд 3

Подготовительные задачи 1. Где расположено множество точек пространства , равноудаленных от двух плоскостей? Теорема 1 Множество точек, равноудаленных от двух параллельных плоскостей ,есть плоскость, параллельная данным плоскостям и проходящая через середину общего перпендикуляра этих плоскостей. Дано : α || β ; γ || α ; γ || β ; AC=CD; AB | α ; AB| β

Слайд 4

Теорема 2 Множество точек, равноудаленных от граней двугранного угла, есть есть биссектриса (биссекторная плоскость) этого двугранного угла.

Слайд 5

Теорема 3 Множество точек, равноудаленных от граней трехгранного угла, есть биссектриса этого трехгранного угла. Биссектрисой трехгранного угла называется луч с началом в вершине данного трехгранного угла, который образует равные углы с гранями этого трехгранного угла.

Слайд 6

Сфера, вписанная в призму Теорема 4 В призму можно вписать сферу тогда и только тогда, когда в перпендикулярное сечение этой призмы можно вписать окружность, и высота призмы равна диаметру этой окружности (диаметру вписанной сферы).

Слайд 7

2. Расстояние между боковыми ребрами треугольной призмы 13,14,15.В призму вписан шар. Боковое ребро составляет с плоскостью основания угол α . Найти объем призмы и объем шара. Решение. (А 2 В 2 С 2 )-перпендикулярное сечение. V ш. = ⁴⁄₃ П R ш. 3 S= ⅟₂ Pr окр R ш.= r впис.окр. = S А2В2С2 / p p =21; S=√p(p-a) (p-b) (p-c); S А2В2С2 =84; R ш. =84 / 21 =4 ; V ш .= ⁴⁄₃ П R ш. 3 ; V ш .= 256 П/3 ; 2) V пр.= S перп.сеч. * АА 1 ; АА 1 = А 1 О/ sin α =8 / sin α ; V пр .=84*8/ sin α =672/ sin α . Ответ : 256 П/3 ; 672/ sin α .

Слайд 8

Сфера, вписанная в пирамиду Боковые грани пирамиды одинаково наклонены к основанию. Теорема 5 Если боковые грани пирамиды одинаково наклонены к основанию(двугранные углы при основании пирамиды равны), то в пирамиду можно вписать сферу, центр которой находится в точке пересечения высоты пирамиды и биссектрисы двугранного угла при основании пирамиды.

Слайд 9

3. Основание пирамиды- треугольник со сторонами 9,10 и 17.Все боковые грани наклонены под углом 45 о к основанию пирамиды .Найти радиус вписанного шара. Решение. 1) OK= r впис.окр . =S/p; S=p* r впис.окр . ;p=18; S=√p(p-a) (p-b) (p-c); S ∆ АВС =36;OK=2. 2) ∆POK: KO ш.-биссектриса, т.о. ООш./Ош. p=OK/PK=cos 45 о ; ООш./Ош. p=1/ √2;

Слайд 10

Теорема 6 В любой тетраэд р можно вписать сферу. Теорема 7 Если в многогранник, объем которого равен V ,а площадь поверхности равна S, вписан шар радиуса R ,то имеет место соотношение : V=⅓S*R 3. Основание пирамиды- треугольник АВС,В котором АВ | ВС,АВ=4,ВС=3.Боковое ребро РА перпендикулярно плоскости основания пирамиды и равно 3.Найдите объем шара, вписанного в пирамиду. Решение. 1) V пир.=⅓ S ∆ ABC *AP; V пир.=⅓*⅟₂*3*4*3=6. 2) PB|BC( по теореме о трех перпендикулярах ); АС= PB=5. 3) S ∆P АВ =S ∆ АВС = ⅟₂ *4*3=6. S ∆P В C = S ∆P А C = ⅟₂ *3*5=7,5. S полн. =2*6+2*7,5=12+15=27. 4)R ш.=3 V пир./ S; R ш.=3*6/27=⅔ ; V ш.=⁴⁄₃П R 3 =32 П/81. Ответ : 32 П/81.

Слайд 11

4 . Шар вписан в прямую призму, основание которой- равнобедренная трапеция с основаниями 2 и 8.Найдите объем шара и объем призмы. Решение. 1) R ш.= r впис.окр . ;H пр.= D впис.окр. =CK. 2)DC+AB=AD+CB; 2BC=2+8; BC=5. 3)BC= ⅟₂(AB-DC); BK= ⅟₂(8-2)=3; 4) ∆BCK:CK=4; R ш. =2. 5)V пр.= S осн.*Нпр. ; V пр.=80 ; V ш.= ⁴⁄₃ П R 3 ; V ш.= ⁴⁄₃ П2 3 =32П/3. Ответ : 32П/3.

Слайд 12

Спасибо за внимание