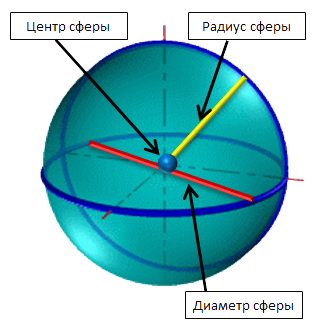
В данной публикации мы рассмотрим, как можно найти площадь шара (сферы) и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади шара/сферы
- 1. Через радиус
- 2. Через диаметр
-
Примеры задач
Формула вычисления площади шара/сферы
1. Через радиус
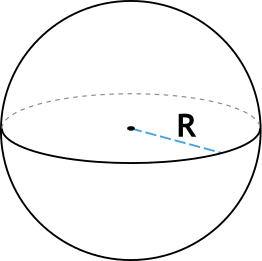
Площадь (S) поверхности шара/сферы равняется произведению четырех его радиусов в квадрате и число π.
S = 4 π R2
Примечание: в расчетах значение числа π округляется до 3,14.
2. Через диаметр
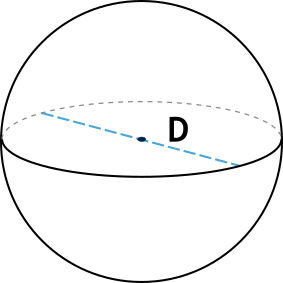
Как известно, диаметр шара/сферы равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь поверхности фигуры можно, используя такой вид формулы:
S = 4 π (d/2)2
Примеры задач
Задание 1
Вычислите площадь поверхности шара, если его радиус составляет 7 см.
Решение:
Воспользуемся первой формулой (через радиус):
S = 4 ⋅ 3,14 ⋅ (7 см)2 = 615,44 см2.
Задание 2
Площадь поверхности сферы равна 200,96 см2. Найдите ее диаметр.
Решение:
Выведем величину диаметра из соответствующей формулы расчета площади:
Шаром называют множество точек, удаленных от произвольно выбранной точки (центра шара) на расстояние не превышающее RR — радиус этого шара.
Онлайн-калькулятор площади поверхности шара
У шара, как и у круга, есть диаметр DD, который по длине в два раза превосходит радиус шара.
D=2⋅RD=2cdot R
Площадь поверхности шара можно найти используя как радиус, так и диаметр шара.
Формула площади поверхности шара по радиусу шара
S=4⋅π⋅R2S=4cdotpicdot R^2
RR — радиус шара.
Шар вписан в куб, диагональ которого dd равна 300sqrt{300} (см.). Найти площадь поверхности шара.
Решение
d=300d= sqrt{300}
Первым шагом в решении задачи будет нахождение длины стороны куба. Обозначим ее через aa. Тогда, по теореме Пифагора:
d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
a=d3a=frac{d}{sqrt{3}}
a=3003=100=10a=frac{sqrt{300}}{sqrt{3}}=sqrt{100}=10
Радиус шара, вписаного в куб равен половине стороны этого куба:
R=a2=102=5R=frac{a}{2}=frac{10}{2}=5
Тогда площадь поверхности шара:
S=4⋅π⋅R2=4⋅π⋅52≈314S=4cdotpicdot R^2=4cdotpicdot 5^2approx314 (см. кв.)
Ответ: 314 см. кв.
Формула площади поверхности шара по диаметру шара
Формулу для площади поверхности шара легко получить через его диаметр, пользуясь соотношением между радиусом и диаметром шара:
S=4⋅π⋅R2=4⋅π⋅(D2)2=π⋅D2S=4cdotpicdot R^2=4cdotpicdotBig(frac{D}{2}Big)^2=picdot D^2
S=π⋅D2S=picdot D^2
DD — диаметр шара.
Диаметр шара равен 10 (см.). Найдите площадь его поверхности.
Решение
D=10D=10
По формуле получаем:
S=π⋅D2=π⋅102≈314S=picdot D^2=picdot 10^2approx314 (см. кв.)
Ответ: 314 см. кв.
Студворк – лучший сайт для заказа контрольных работ!
Тест по теме «Площадь поверхности шара»
Площадь поверхности шара, или как часто неправильно говорят просто площадь шара, вычисляется по очень простой формуле. Но даже простые вещи можно упростить и именно поэтому мы сделали калькулятор, который в режиме онлайн может рассчитать площадь поверхности шара, а также на странице вы найдете формулу для расчета.
Возможно вам дополнительно потребуется рассчитать и объем шара.
Шар — геометрическое тело, состоящее из точек пространства, которые удалены от центра на расстояние, не более заданного. Это расстояние называют радиусом шара.
Содержание:
- калькулятор площади поверхности шара
- формула площади поверхности шара через радиус
- формула площади поверхности шара через диаметр
- формула площади поверхности шара через длину окружности
- примеры задач
Формула площади поверхности шара через радиус
{S = 4pi R^2}
R – радиус шара
Формула площади поверхности шара через диаметр
{S = pi D^2}
D – диаметр шара
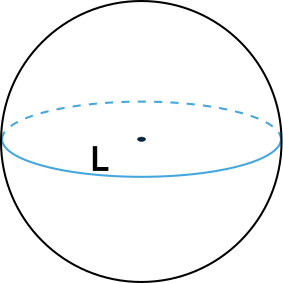
Формула площади поверхности шара через длину окружности
{S = dfrac{L^2}{pi}}
L – длина окружности шара
Примеры задач на нахождение площади поверхности шара
Задача 1
Найдите площадь поверхности шара диаметром 10см.
Решение
Так как в условии дан диаметр шара, мы воспользуемся второй формулой.
S = pi D^2 = pi cdot 10^2 = pi cdot 100 = 100pi : см^2 approx 314.15927 : см^2
Ответ: 100pi : см^2 approx 314.15927 : см^2
калькулятор поможет проверить правильность вычислений.
Задача 2
Найдите площадь поверхности шара, если его радиус равен 5см.
Решение
В этой задаче мы будем использовать первую формулу.
S = 4pi R^2 = 4pi cdot 5^2 = 4pi cdot 25 = 100pi : см^2 approx 314.15927 : см^2
Ответ: 100pi : см^2 approx 314.15927 : см^2
Проверка ответа.
Площадь поверхности шара
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности шара
Чтобы посчитать площадь поверхности шара (площадь сферы) воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чему равна площадь поверхности шара, если:
=
S =
0
Округление числа π: Округление ответа:
Просто введите известный вам параметр, и узнаете площадь сферы шара.
Теория
Ликбез: Поверхность шара — сфера.
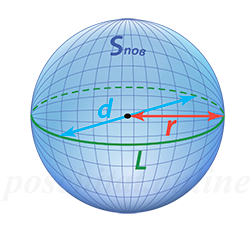
Площадь поверхности шара через радиус
Чему равна площадь поверхности шара Sпов, если его радиус r:
Формула
Sпов = 4⋅π⋅r² , где π ≈ 3.14…
Пример
Для примера посчитаем какая площадь поверхности у шара, если его радиус r = 3 см:
Sпов = 4 ⋅ 3.14 ⋅ 3² = 12.56 ⋅ 9 = 113.04 см²
Площадь поверхности шара через диаметр
Чему равна площадь поверхности шара Sпов, если его диаметр d?
Формула
Sпов = π⋅d² , где π ≈ 3.14…
Пример
Для примера посчитаем какая площадь поверхности у шара, если его диаметр d = 6 см:
Sпов = 3.14 ⋅ 6² = 3.14 ⋅ 36 = 113.04 см²
Площадь поверхности шара через длину окружности
Чему равна площадь поверхности шара Sпов, если длина его окружности L?
Формула
Sпов = L²⁄π , где π ≈ 3.14…
Пример
Для примера посчитаем чему равна площадь поверхности шара, имеющего длину окружности L = 10 см:
Sпов = 10² ⁄ 3.14 ≈ 31.85 см²
См. также
Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас
слышал про эту знаменитую спортивную игру. Всем известно,
что в футбол играют мячом.
Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть
людей скажут, что форму шара, а часть, что формы сферы. Так кто же
из них прав? И в чем разница между сферой и шаром?
Важно!
Шар — это пространственное тело. Внутри шар
чем-либо заполнен. Поэтому у шара можно найти объем.
Примеры шара в жизни: арбуз и стальной шарик.
Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.
Важно!
Сфера — поверхность шара. У сферы можно найти площадь поверхности.
Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный
теннис.
Как найти площадь сферы
Запомните!
Формула площади сферы:
S = 4πR2
Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа.
Зная определение степени,
можно записать формулу площади сферы следующим образом.
S = 4π R2 =
4πR · R;
Закрепим полученные знания и решим задачу на площадь сферы.
Зубарева 6 класс. Номер 692(а)
Условие задачи:
-
Вычислите площадь сферы, если её радиус равен
1 м. (возьмите π как
3)
Вспомнив, как выделить целую часть
и перемножить дроби,
воспользуемся формулой площади сферы:
S = 4 · πR2 =
4 · 3 ·
(1 ) 2 =
4 · ·
() 2 =
4 · ·
=
=
= =
=
=
45
м2
Как найти объем шара
Запомните!
- Формула объема шара:
V = πR3
Зная определение степени,
можно записать формулу объема шара следующим образом.
-
V =
π R3 =π R · R · R;
Для отработки полученных знаний решим задачу на объем шара.
Зубарева 6 класс. Номер 691(а)
Условие задачи:
-
Вычислите радиус шара, если его объем равен
4 м3 (возьмите π как
3)
Выразим из формулы объема шара радиус.
- V =
π R3 -
π R3
= V -
π R3
=
-
R3
=
Подставим в формулу известные нам значения. Число π
возьмем как задано в задании «3».
R3
= (3 ·
4) /
(4 · 3)
Чтобы не запутаться, отдельно рассчитаем
числитель дроби.
3 ·
4 =
3 ·
=
=
Теперь снова подставим полученное значение в нашу формулу:
-
R3
=
/ (4 · 3)=
/ (4 · )
=
/ () =
=
· () =
= =
=
= 1
- R3 = 1
- R = 1 м
Важно!
Уважаемые родители!
При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.
В 6 классе при решении такой задачи используйте метод перебора.
Спросите ученика, какое число, если его умножить 3 раза на самого себя даст
единицу.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
14 февраля 2019 в 22:59
Руслан Магомедов
Профиль
Благодарили: 0
Сообщений: 1
Руслан Магомедов
Профиль
Благодарили: 0
Сообщений: 1
Рассчитайте объем чашки высотой 7 см с диаметром 6,5 с
0
Спасибо
Ответить