Как найти площадь шарового слоя

Как найти площадь шарового слоя

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности шарового слоя (среза шара): сферической, оснований и полную.

  • Определение шарового слоя

  • Формула для нахождения площади шарового слоя

    • Сферическая поверхность

    • Основания

    • Полная поверхность

Определение шарового слоя

Шаровый слой (или срез шара) – это часть шара, оставшаяся между двумя  пересекающими его параллельными плоскостями. На рисунке ниже окрашен в желтый цвет.

Шаровый слой (срез шара)

  • R – радиус шара;
  • r1 – радиус первого основания среза;
  • r2 – радиус второго основания среза;
  • h – высота шарового слоя; перпендикуляр от центра первого основания до центра второго.

Формула для нахождения площади шарового слоя

Сферическая поверхность

Чтобы найти площадь сферической поверхности шарового слоя, нужно знать радиус шара, а также высоту среза.

Sсфер. пов. = 2πRh

Основания

Площадь оснований среза шара равняется произведению квадрата соответствующего радиуса на число π.

S1 = πr12

S2 = πr22

Полная поверхность

Площадь полной поверхности шарового слоя равна сумме площадей ее сферической поверхности и двух оснований.

Sполн. пов. = 2πRh + πr12 + πr22 = π(2Rh + r12 + r22)

Примечания:

  • если вместо радиусов (R, r1 или r2) даны диаметры (d), последние следует разделить на 2, чтобы найти нужные значения радиусов.
  • значение числа π при выполнении расчетов обычно округляется до двух знаков после запятой – 3,14.
Источник

Как рассчитать площадь шарового слоя

На данной странице можно быстро и точно рассчитать площадь шарового слоя онлайн. Для этого нужно знать радиус и высоту.
На данной странице калькулятор поможет рассчитать площадь поверхности шарового слоя онлайн. Для расчета задайте радиус и высоту.

Шаровой слой — это часть шара, ограниченная двумя секущими параллельными плоскостями.

Через радиус и высоту

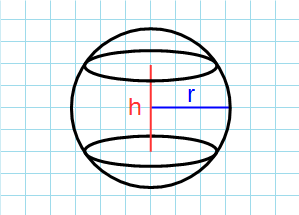
Площадь шарового слоя

Формула площади шарового слоя через радиус и высоту:

π – константа равная (3.14); r – радиус шара; h – высота шарового сегмента.

Источник

Площадь поверхности шарового слоя, формула

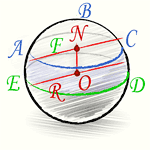
Площадь поверхности шарового слоя

Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями.
Шаровой пояс или Шаровая зона — это кривая поверхность шарового слоя. Круги ABC и DEF это основания шарового пояса. Расстояние между основаниями это высота шарового слоя.

Кривая поверхность шарового слоя равна произведению его высоты на окружность большого круга шара:

[ S = 2pi R h ]

(R – радиус большого круга шара, h=NO – высота шарового слоя)

Формулы шара, сферы

Вычислить, найти площадь поверхности шарового слоя по формуле (1)

Ссылки по теме

Площадь поверхности шарового слоя

 стр. 316
Источник

({color{red}{{small{textbf{Факт 1. Про шаровой сегмент}}}}})
(bullet) Шаровой сегмент – шасть шара, отсекаемая от него плоскостью ((alpha)).

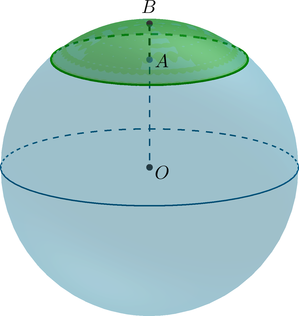
(bullet) Если (O) – центр шара, (OB=R) – радиус шара, перпендикулярный плоскости (alpha), (A) – центр круга (основания шарового сегмента), а также точка пересечения радиуса (OB) c этим кругом, то
(H=AB) – высота шарового сегмента.
(bullet) Площадь сферического сегмента (часть сферы, отсекаемая от нее плоскостью (alpha)) вычисляется по формуле [S=2pi cdot RH] (bullet) Объем шарового сегмента вычисляется по формуле [V=pi H^2cdot left(R-frac13Hright)]

({color{red}{{small{textbf{Факт 2. Про шаровой слой}}}}})
(bullet) Шаровой слой – часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.

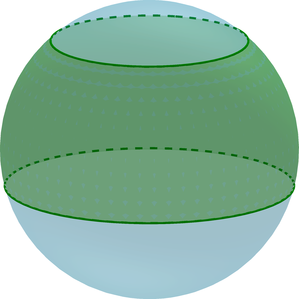
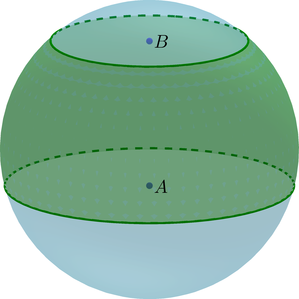
(bullet) Основания шарового слоя – это сечения шара плоскостями.
(bullet) Высота (H=AB) шарового слоя – это расстояние между основаниями.
(bullet) Площадь сферической части шарового слоя равна [S=2pi RH] где (R) – радиус шара.
(bullet) Объем шарового слоя равен разности объемов двух шаровых сегментов: [V=V_{A}-V_{B}]

({color{red}{{small{textbf{Факт 3. Про шаровой сектор}}}}})
(bullet) Шаровой сектор – часть шара, ограниченная сферической частью шарового сегмента и боковой поверхностью конуса, имеющего то же основание, что и шаровой сегмент.

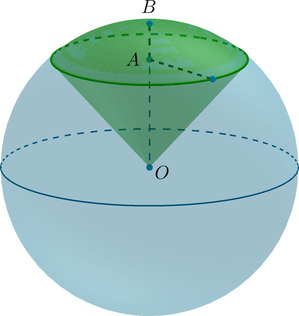
(bullet) Если (H=AB), то объем шарового сектора равен [V=dfrac23pi R^2cdot H]

Источник

Шаровой слой

Шар пересеченный двумя параллельными плоскостями

Шаровой слой — часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар[1].

Содержание

  • 1 Связанные определения
  • 2 Свойства
  • 3 Вариации и обобщения
  • 4 См. также
  • 5 Примечания

Связанные определения[править | править код]

  • Основания шарового слоя — это сечения шара, образовавшиеся в результате пересечения шара двумя параллельными плоскостями.
  • Высота шарового слоя — это расстояние между основаниями слоя.

Свойства[править | править код]

  • Объём шарового слоя можно найти как разность объёма двух шаровых сегментов:
        V=pi left[H_{1}^{2}left(R-{frac {1}{3}}H_{1}right)-H_{2}^{2}left(R-{frac {1}{3}}H_{2}right)right],
    где V — объём шарового слоя, H_1 — высота большего шарового сегмента, H_2 — высота меньшего шарового сегмента, R — радиус шара.
  • Площадь сферической части поверхности шарового слоя (так называемый сферический пояс) зависит только от высоты слоя и радиуса шара[2]:
    S=2pi Rh,
где S — площадь сферического пояса, h — высота шарового слоя, R — радиус шара.

Вариации и обобщения[править | править код]

  • В физике под шаровым слоем часто понимают слой, ограниченный сферами радиуса r и r+dr, для маленького dr. Объем шарового слоя в этом случае с точностью до O{displaystyle (dr^{2})} равен dV=4pi r^{2}dr.

См. также[править | править код]

  • Сферический слой

Примечания[править | править код]

  1. ↑ Мантуров О. В. и др. Словарь математических терминов. — М.: Просвещение, 1965. — С. 512.
  2. ↑ Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров. — М.: Советская энциклопедия, 1988. — С. 638.
Источник

Добавить комментарий