Как найти площадь шейки

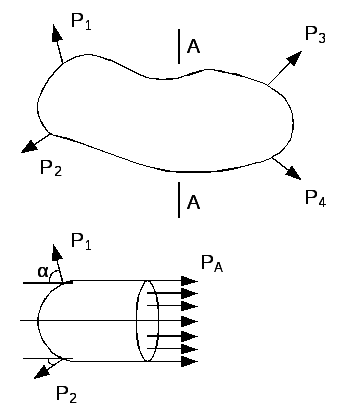
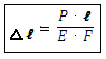Метод сечений.

Под
действиями внешних нагрузок в теле
возникают внутренние усилия. Для их
определения будем использовать метод
сечения или метод
Розу:

1. Разрезаем мысленно тело сечением А.

2. Отбрасываем одну часть.

3. Действия отброшенной части заменяют
   системой внутренних сил.

4. Составляем уравнения равновесия
   отсеченной части, из которых находят
   внутренние усилия.

Составляется уравнение равновесия:

P_1∙cos
α
+P_2
∙ cos
γ
– P_A=0.
Из которого находят
неизвестное Р_А.

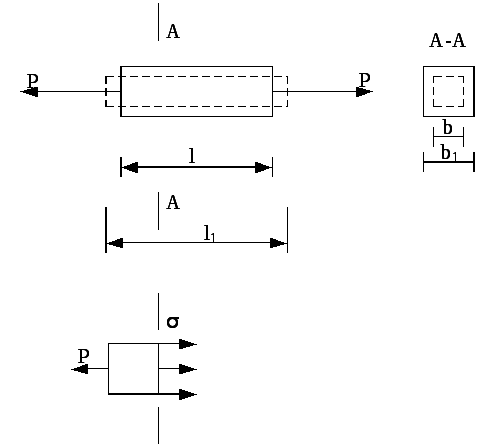
Понятие о напряжениях.

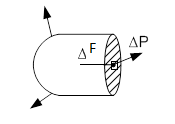
Обозначим P
– сила, F
– площадь сечения.

Выделим в сечении бесконечно
малый элемент площадью _ΔF,
тогда среднее напряжение равно σ_ср=.Уменьшая _ΔF
найдем испытанное
напряжение.

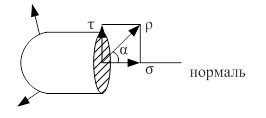
Разложим напряжение р
на составляющие σ
и
τ
. Тогда полное напряжение можно найти:

р=

σ
= p×cosα
– нормальное
напряжение.

τ
=p×sinα
– касательное
напряжение.

Классификация внешних сил.

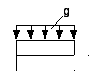
1. Сосредоточенные силы –
   нагрузки, прикладываемые по малой
   площади, обозначаем

P
(H,
кН, мН)

1. Распределенные нагрузки

а) равномерно
распределенные по длине
ɡ
(н/м, кН/см)

b)
Равномерно распределенные
по площади ɡ
(н/м ²,
кН/см²).

с) неравномерно
распределенные по
площади или по длине.

1. По времени действийнагрузки могут
   быть:

1. Постоянные –
   не меняют свою величину (вес перекрытия)

2. Временные – исчезают или появляются
   с течением времени ( вес людей на
   перекрытии).

1. По способу приложения:

1. Статические– прикладываются
   постепенно.

2. Динамические –
   прикладываются в течение короткого
   времени(удар).

Растяжение и сжатие. Продольные и поперечные деформации. Напряжение.

Например:

μ= 0,5
– для резины

μ=0,3
– для стали

μ=0
– для пробки

σ
=–нормальное
напряжение, где F–начальная
площадь поперечного сечения стержня.

В1678 Роберт Гук заметил, что между
напряжением и деформацией существует
линейная зависимость:σ=
Е×ε – закон
Гука

где Е–модуль упругости
материала, постоянное число для данного
материала. Е=2,1×10⁶=2,1×10⁴

– закон
Гука в другом виде.

Примечание: при растяжении
справедлива гипотеза
плоских сечений
(гипотеза Я. Бернулли)
– плоские сечения
до деформаций остаются плоскими и после
деформаций. Все волокна удлинняются
одинаково.

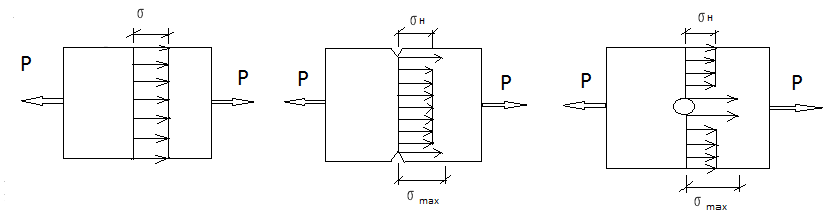
Концентрация напряжений.

При осевом растяжении или сжатии
нормальные напряжения распределяются
равномерно в поперечном сечении
призматических стержней. Если же в
стержне имеется отверстие или выточка,
то напряжения в сечении распределяются
неравномерно: около отверстия или
выточек появляется повышенное напряжение.

а
=σ_max/σ
_н
– коэффициент
концентрации напряжений.

σ_н
= Р/А_н,
где
А_н
(нетто) –
площадь сечения
в ослабленном месте.

Концентрация напряжения
опасна для хрупких материалов, а в
пластичных материалах после достижения
σ_max=σ_{текучести},
напряжения дальше не растут, а
увеличиваются напряжения в других
точках поперечного сечения.

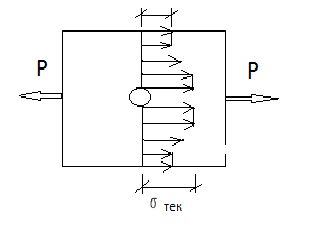
Напряжения и деформации при действии
равномерно распределенной осевой
нагрузки

Найдем напряжение и деформации в начале
для сечения находящегося на расстоянии
xот свободного конца.

-сила

При x=0;N=0;

При X=;
q;

Переходим к определению
деформаций.

Вначале найдем удлинение
участка dx

– закон Гука (собственным
весом участка пренебрегаем).

Удлинение участка (-x)
получим если последнее выражение
проинтегрируем от x
до

–
удлинение участка (-x)

X=0
тогда

X=тогда
=0

f=f–стрела параболы

В свободном конце стержня перемещения
можно определить по формуле

– площадь эпюры.

Если в качестве распределенной нагрузки
служит плотность материала стержня
,то

(умножим
числитель и знаменатель на А).

Пусть
– собственный вес стержня.

–деформация от собственного веса.

Ранее получили что при растяжении
стержня силой Р деформации равны
.

Вывод:как видно деформации от
собственного веса стержня получаются
в 2 раза меньше деформации от силы Р.

Опытное изучение растяжение
материалов. Диаграммы напряжений

Механические свойства материалов
выявляются при испытании их под нагрузкой.
Наиболее распространенным видом
испытаний являются испытания на
растяжение. Это объясняется тем, что
мех. свойства мат-лов полученные при
испытании на растяжение во многих
случаях позволяют достаточно полно
судить о поведении материалов при других
видах деформации. С другой стороны
испытания на растяжении легко осуществимы.

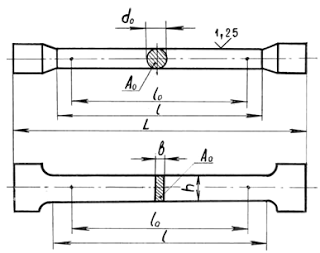
Для испытаний берут образцы стандартных
размеров

-общая
длина образца

Для стандартных образцов

Чаще всего испытывают образцы диаметром
d=1см. Испытания осуществляют
на специальных испытательных машинах.
Многие машины автоматически вычерчивают
графики зависимости нагрузки от
деформации.

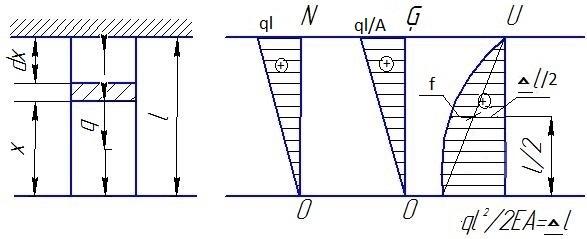
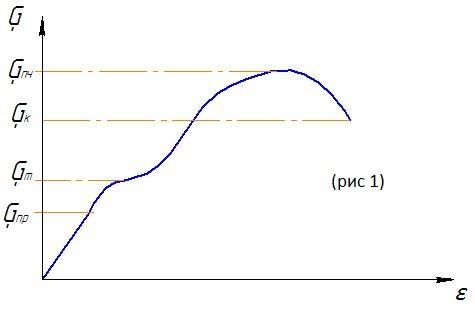
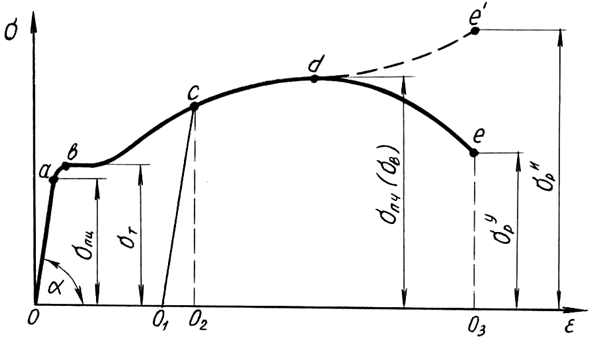
Ниже рассмотрим диаграмму растяжения
малоуглеродистой стали.

Рассмотрим характерные участки и точки
этой диаграммы.

На участке ОА деформации растут
пропорционально нагрузкам, следовательно
до точки А справедлив закон Гука. Точка
А соответствует пределу пропорциональности

– предел пропорциональности.

На участке АВ линейная зависимость
между Р и
нарушается. Однако до точки В возникают
в образце упругие деформации. Это
означает, если образец нагрузить до
точки В, а затем разгрузить, то деформации
в образце исчезнут (образец примет
первичную форму– предел упругости.

В окрестности точки С имеется почти
горизонтальная площадка, здесь деформации
растут без видимого увеличения нагрузки.
Эта площадка называется площадкой
текучести. На поверхности образца
появляются наклонные линии. Впервые
эти линии заметил русский металлург
Чернов. Независимо от него так же заметил
Людекс. (Линии Людекса-Чернова)

Точка С – соответствует пределу
текучести.

– предел текучести

За площадкой текучести для дальнейшего
деформирования образца необходимо
увеличить нагрузку.

Точка D– соответствует
пределу прочности.

– предел прочности (временного
сопротивления).

–
наибольшая нагрузка, которую образец
выдержал при испытаниях.

Начиная с точки Dв образце
появляется шейка (местное сужение).

На участке DKдеформации
растут в районе шейки.

В точке К образец разрушается

,
где–
напряжение в момент разрушения.

А – площадь поперечного сечения шейки
в момент разрушения.

КЕ || ОА

На участке ОЕ возникают остаточные
деформации

Замечания:

1. Если образец нагрузить до точки Т, а
   затем разгрузить, то диаграмма пойдет
   по линии

TL||OA. При
повторном нагружении этого образца
карандаш пойдет по линииLTDK.

Как видно в этом случае площадка текучести
исчезнет и упругие свойства материала
возрастают. Это явление называется
наклепом и широко используется в
строительстве.

Например арматуру железо-бетонных
конструкций предварительно напрягают.

1. Если после разгрузки дать образцу
   возможность «отдохнуть» (не менее 100
   часов) , то при повторном нагружении
   диаграмма пойдет по линии LTM.
   Это явление называется явлениемстарения.

По результатам испытаний можно судить
о прочности упругости и пластичности
материала.

Прочность характеризуется величинамии

Упругость характеризуется

Пластичность характеризуетсяи

Где
– остаточное относительное удлинение

– относительное сужение.

Где
,
А – площадь поперечного сечения до
деформации,-площадь
после деформации.

– для пластичного материала

– для хрупких материалов

Диаграмма напряжений.

Рассмотренная в предыдущем параграфе
диаграмма растяжения зависит от размеров
образца. Для того чтобы исключить влияние
размеров образца на форму диаграммы
иногда ее представляют в координатах
и

Ниже рассмотрим диаграммы напряжений
для некоторых материалов

tg

Из закона Гука известно

– модуль упругости

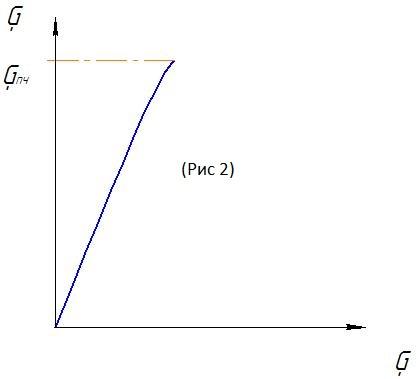
Диаграмма напряжения хрупкого материала
(чугун)

Как видно из рис.2 для хрупких материалов
площадка текучести отсутствует,
следовательно нет предела текучести.
Также видно, что хрупкие материалы при
растяжении разрушаются при малых
деформациях

Диаграмма растяжения бетона

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Площадь – сечение – шейка

Cтраница 1

Площадь сечения шейки, соединяющей прибыль с отливкой, должна быть: у тела отливки – 0 3 – 0 4, у основания прибыли – 0 35 – 0 5 площади сечения прибыли.
 [1]

Площадь сечения шейки уменьшается, и для доведения образца до разрушения требуется сила меньше F nax; это отмечает участок диаграммы, отклоняющийся вниз к оси абсцисс. Действительные напряжения в сечении шейки не уменьшаются, а все время растут; площадь сечения шейки уменьшается более интенсивно, чем растягивающая сила F. Точка G соответствует разрушению образца.
 [2]

При отнесении силы Р к площади сечения образующейся шейки такие напряжения являются средними по сечению.
 [3]

Для суждения о прочности стержня по величине истинного напряжения при разрыве следует знать площадь сечения шейки в месте разрыва; эта площадь не может быть заранее, при проектировании или изготовлении стержня, точно предугадана. Эта сила характеризует прочность стержня.
 [4]

Чтобы судить о прочности стержня по величине истинного напряжения при разрыве, необходимо знать площадь сечения шейки в месте разрыва. Эта площадь не может быть заранее, при проектировании или изготовлении стержня, точно предугадана. Величина же временного сопротивления, умноженная на первоначальную площадь поперечного сечения проектируемого или изготовленного стержня, дает достаточно точное представление о величине той наибольшей растягивающей силы, которую может выдержать стержень без разрушения. Эта сила характеризует прочность стержня.
 [5]

Бриджмен установил, что предельная пластичность, определяемая как логарифм отношения начальной площади поперечного сечения образца к площади сечения шейки в момент разрыва, связана с гидростатическим давлением линейной зависимостью епл е – f – ПР гДе 8 – деформация при разрыве без давления; п – коэффициент пропорциональности.
 [6]

Отметив точки с и Ъ на концах диаметра, перпендикулярного О а через них и точку а проводится дуга окружности Ьа с, которая отсекает от площади сечения шейки серповидную фигуру. Эта фигура принимается за эпюру давления на шейку. Местные износы поверхности последней предполагаются пропорциональными отрезками Др этой эпюры. Такие же серповидные фигуры строятся для всех векторов векторной диаграммы ( фиг.
 [7]

Для определения FK обе части образца после разрыва плотно складывают и в случае цилиндрических образцов измеряют диаметр шейки в двух взаимно перпендикулярных направлениях. По среднему арифметическому двух наименьших значений диаметра вычисляют площадь сечения шейки образца после разрыва.
 [8]

Площадь сечения шейки уменьшается, и для доведения образца до разрушения требуется сила меньше F nax; это отмечает участок диаграммы, отклоняющийся вниз к оси абсцисс. Действительные напряжения в сечении шейки не уменьшаются, а все время растут; площадь сечения шейки уменьшается более интенсивно, чем растягивающая сила F. Точка G соответствует разрушению образца.
 [9]

На образце при этом значении силы образуется резкое местное сужение, так называемая шейка, намечается место последующего разрыва. Образец сильно удлиняется за счет пластической деформации шейки. Площадь сечения шейки уменьшается, и для доведения образца до разрушения требуется сила меньше Яшах; это отмечает участок DE диаграммы, отклоняющийся вниз, к оси абсцисс. Точка Е соответствует разрушению образца.
 [10]

Точка D диаграммы определяет наибольшее для данного испытания значение силы Ргаах. На образце при этом значении силы образуется резкое местное сужение, так называемая шейка, намечается место последующего разрыва. Образец сильно удлиняется за счет пластической деформации шейки. Площадь сечения шейки уменьшается, и для доведения образца до разрушения требуется сила, меньшая Ршах; это отмечается участком DE диаграммы, отклоняющимся вниз, к оси абсцисс.
 [11]

С появлением шейки нагрузка начинает падать, поэтому и условные напряжения на участке DE падают, так как диаграмму строят без учета изменения площади сечения образца. Напряжение в точке Е диаграммы называют напряжением разрушения материала. Но это напряжение чисто условное. Истинное напряжение в момент разрушения значительно превосходит не только условное напряжение, но и предел прочности и равно отношению разрушающей нагрузки к площади сечения шейки.
 [12]

Вслед за площадкой текучести ВС следует пологий криволинейный участок диаграммы CD; удлинения растут с увеличением силы, но материал уже не следует закону Гука; кроме упругого удлинения, образец получает значительное остаточное удлинение. Участок CD соответствует стадии упрочения материала образца. Точка D диаграммы определяет наибольшее для данного испытания значение силы Ршах. На образце при этом значении силы образуется резкое местное сужение, так называемая шейка, намечается место последующего разрыва. Образец сильно удлиняется за счет пластической деформации шейки. Площадь сечения шейки уменьшается, и для доведения образца до разрушения требуется сила, меньшая Ртах; это отмечается участком DE диаграммы, отклоняющимся вниз, к оси абсцисс.
 [13]

Страницы:  

   1

Лабораторная работа №1 по испытанию на растяжение и разрыв стального образца из малоуглеродистой стали (видео).

Цель работы – изучить поведение малоуглеродистой стали при растяжении и определить ее механические характеристики.

Скачать журнал испытания стали на растяжение

Основные сведения

Испытания на растяжение являются основным и наиболее распространенным методом лабораторного исследования и контроля механических свойств материалов.

Эти испытания проводятся и на производстве для установления марки поставленной заводом стали или для разрешения конфликтов при расследовании аварий.

В таких случаях, кроме металлографических исследований, определяются главные механические характеристики на образцах, взятых из зоны разрушения конструкции. Образцы изготавливаются по ГОСТ 1497-84 и могут иметь различные размеры и форму (рис. 1.1).

Рис. 1.1. Образцы для испытания на растяжение

Между расчетной длиной образца l_о и размерами поперечного сечения А_о (или d_о для круглых образцов) выдерживается определенное соотношение:

В испытательных машинах усилие создается либо вручную — механическим приводом, либо гидравлическим приводом, что присуще машинам с большей мощностью.

В данной работе используется универсальная испытательная машина УММ-20 с гидравлическим приводом и максимальным усилием 200 кН, либо учебная универсальная испытательная машина МИ-40КУ (усилие до 40 кН).

Порядок выполнения и обработка результатов

Образец, устанавливаемый в захватах машины, после включения насоса, создающего давление в рабочем цилиндре, будет испытывать деформацию растяжения. В измерительном блоке машины есть шкала с рабочей стрелкой, по которой мы наблюдаем рост передаваемого усилия F.

Другие видео

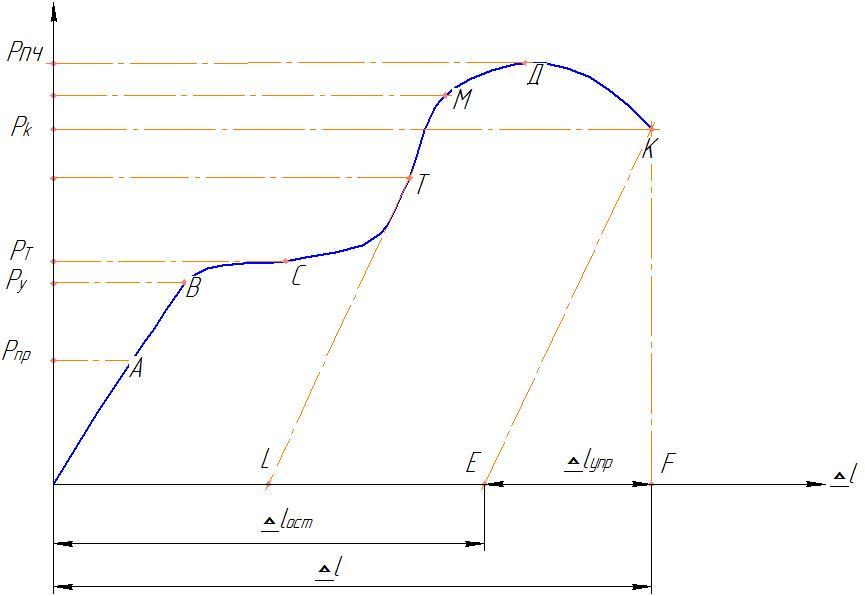
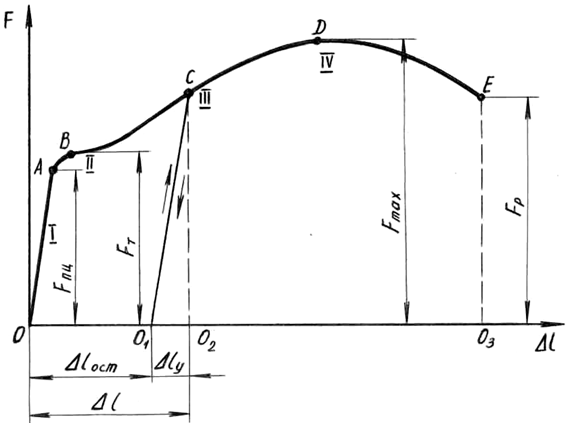
Зависимость удлинения рабочей части образца от действия растягивающей силы во время испытания отображается на миллиметровке диаграммного аппарата в осях F-Δl (рис. 1.2).

В начале нагружения деформации линейно зависят от сил, потому участок I диаграммы называют участком пропорциональности. После точки В начинается так называемый участок текучести II.

На этой стадии стрелка силоизмерителя как бы спотыкается, приостанавливается, от точки В на диаграмме вычерчивается либо прямая, параллельная горизонтальной оси, либо слегка извилистая линия — деформации растут без увеличения нагрузки. Происходит перестройка структуры материала, устраняются нерегулярности в атомных решетках.

Далее самописец рисует участок самоупрочнения III. При дальнейшем увеличении нагрузки в образце происходят необратимые, большие деформации, в основном концентрирующиеся в зоне с макронарушениями в структуре – там образуется местное сужение — «шейка».

На участке IV фиксируется максимальная нагрузка, затем идет снижение усилия, ибо в зоне «шейки» сечение резко уменьшается, образец разрывается.

При нагружении на участке I в образце возникают только упругие деформации, при дальнейшем нагружении появляются и пластические — остаточные деформации.

Если в стадии самоупрочнения начать разгружать образец (например, от т. С), то самописец будет вычерчивать прямую СО₁. На диаграмме фиксируются как упругие деформации Δl_у (О₁О₂), так и остаточные Δl_ост (ОО₁). Теперь образец будет обладать иными характеристиками.

Так, при новом нагружении этого образца будет вычерчиваться диаграмма О₁CDЕ, и практически это будет уже другой материал. Эту операцию, называемую наклеп, широко используют, например, в арматурных цехах для улучшения свойств проволоки или арматурных стержней.

Диаграмма растяжения (рис. 1.2) характеризует поведение конкретного образца, но отнюдь не обобщенные свойства материала. Для получения характеристик материала строится условная диаграмма напряжений, на которой откладываются относительные величины – напряжения σ=F/A₀ и относительные деформации ε=Δl/l₀ (рис. 1.3), где А₀, l₀ – начальные параметры образца.

Рис. 1.2. Диаграмма растяжения образца из малоуглеродистой стали

Рис. 1.3. Условная диаграмма напряжений при растяжении

Условная диаграмма напряжений при растяжении позволяет определить следующие характеристики материала (рис. 1.3):

σ_пц – предел пропорциональности – напряжение, превышение которого приводит к отклонению от закона Гука. После наклепа σ_пц может быть увеличен на 50-80%;

σ_у – предел упругости – напряжение, при котором остаточное удлинение достигает 0,05%. Напряжение σ_у очень близко к σ_пц и обнаруживается при более тонких испытаниях. В данной работе σ_у не устанавливается;

σ_т – предел текучести – напряжение, при котором происходит рост деформаций при постоянной нагрузке.

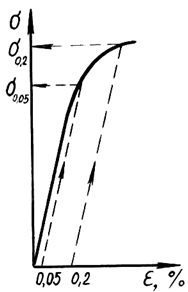
Иногда явной площадки текучести на диаграмме не наблюдается, тогда определяется условный предел текучести, при котором остаточные деформации составляют ≈0,2% (рис. 1.4);

Рис. 1.4. Определение предела упругости и условного предела текучести

σ_пч (σ_в) – предел прочности (временное сопротивление) – напряжение, соответствующее максимальной нагрузке;

σ_р – напряжение разрыва. Определяется условное σ^у_р и истинное σ^и_р=F_р/А_ш, где А_ш – площадь сечения «шейки» в месте разрыва.

Определяются также характеристики пластичности – относительное остаточное удлинение

δ = (l₁ – l₀)∙100% / l₀,

где l₁ – расчетная длина образца после разрыва,
и относительное остаточное сужение

ψ = (А₀ — А_ш)∙100% / А₀.

По диаграмме напряжений можно приближенно определить модуль упругости I рода

E=σ_пц/ε=tgα,

причем после операции наклепа σ_пц возрастает на 20-30%.

Работа, затраченная на разрушение образца W, графически изображается на рис. 1.2 площадью диаграммы OABDEO₃. Приближенно эту площадь определяют по формуле:
W = 0,8∙F_max∙Δl_max.

Удельная работа, затраченная на разрушение образца, говорит о мере сопротивляемости материала разрушению w = W/V, где V = A₀∙l₀ – объем рабочей части образца.

По полученным прочностным и деформационным характеристикам и справочным таблицам делается вывод по испытуемому материалу о соответствующей марке стали

Контрольные вопросы

Испытание материалов на сжатие >
Краткая теория >
Примеры решения задач >

перейти к полному списку дипломных проектов

Ссылка на скачивания файла в формате .doc находится в конце странички

9 – Зонт трапециевидный

Sзонт = сумма площадей всех сторон (трапеций) (1.2)

Площадь каждой стороны (трапеции) вычисляется по формуле: ((a*b)/2)*h, где

A – длина нижнего основания трапеции(стороны);

B – длина верхнего основания трапеции;

H – высота трапеции.

Вычисление площади зонта 2 вид (конусообразный)

Sкруга

Sсегм

Рисунок 1.10 – Зонт конусообразный

Для изготовления конусообразного зонта из куска металла вырезается круг определенного диаметра. Затем из этого круга вырезается определенной величины сегмент. После чего обрезанные края круга зигуются, соединяются вместе и сбиваются. Полученный результат (заготовку) можно увидеть на рис. 1.10.

Площадь конуса можно вычислить по формулам:

Sкруг = ?R2 – площадь круга

Sсегм = (?R2 /360) * a, где a – угол сегмента выраженный в градусах

Sзонт = Sкруг – Sсегм (1.3)

Вычисление площади зонта 3 вид (пирамидальный)

h

a

Рисунок 1.11 – Зонт пирамидальный

Sзонт = сумма площадей всех сторон (равнобедренных треугольников) (1.4)

Sстор = ? * a * h, где a – основание; h – высота треугольника

Sзонт = Sa * 2 + Sb * 2

Вычисление площади отвода с прямой шейкой

Затылочная часть (затылок)

Фасонная часть

Шеечная часть (шейка)

Рисунок 1.12 – Отвод

При вычислении площади отвода с прямой шейкой сначала вычисляется площадь “шейки”, затем площадь “затылка” и после чего вычисляется площадь фасонной части. Площади “затылка” и “шейки” вычисляются легко. Они представляют собой прямоугольники, вырезанные из металла и вычисляются по формуле

S = a * b,

где a и b являются смежными сторонами прямоугольника. Труднее вычисляется площадь фасонной части. Сначала вычисляется периметр одной стороны шейки затем другой стороны шейки (в случае если шейка одинакова с обеих сторон). Затем как видно на рис. 1.5.5 остается вычислить площадь сегмента, которая вычисляется по формуле

Sсегм = (?R2 /360) * a.

Общая площадь получается из суммы частей всех вычисленных площадей и представляет собой формулу:

Sотв. = Sш. + Sз. + Sф. где (1.5)

Sш. – площадь шейки;

Sз. – площадь затылка;

Sф. – площадь фасонной части.

Далее

Sш. = Sз.= a * b,

где a и b стороны прямоугольника. Особое внимание уделяется вычислению площади фасонной части как видно на рис 1.5.6 она состоит из трех частей – Sсегм, S1, S2 и вычисляется по формуле:

Sф. = (Sсегм * 2) + S1 + S2 где (1.6)

Sсегм = (?R2 /360) * a.

S1 = S2 = a * b, где

сторона a = высоте фасонной части отвода;

сторона b = половине длины шейки.

S1

Площадь сегмента a

a b

S2 b

Рисунок 1.

скачать бесплатно Разработка АРМ мастера строительно-монтажных работ структурного подразделения ОАО «Сургутнефтегаз»

Содержание дипломной работы

Большая часть работы мастера связана с накоплением большого количества информации связанным с производством, таким как ведение документации по каждому строящемуся или ремонтируемому объекту
Но так как, бригаде нельзя простаивать, то все приступают к изготовлению следующего заказа, который лежит на столе заказов
Основной профиль работ Специализированного управления – это сантехника, электромонтажные работы, термоизоляция, вентиляция
;
Каждую готовую деталь подписывают (строго обязательно): номер детали, наименование объекта (сокращенно) и номер партии;
Каждую подписанную деталь составляет в партии

Пояснения к таблице: Обозначаемые во второй строке в слове партия буквы обозначают: В – вытяжка, ВЕ – вытяжка естественная, П – приточка, ДУ – дымоудаление

Наименование заготовок подлежащих к вычислению их площадей: Труба (прямик), зонт (три вида), отвод, переход (два вида), утка

S1 = S2 = a * b, где

сторона a = высоте фасонной части отвода;
сторона b = половине длины шейки
В роли интерпретатора команд xBase выступает обычно либо среда разработки приложения на этом языке, либо среда времени выполнения

Windows-версии СУБД Paradox, помимо перечисленных выше сервисов, позволяли также манипулировать данными других форматов, в частности dBase и данными, хранящимися в серверных СУБД

Во внутримашинной информационной базе осуществляется контроль целостности данных с помощью бизнес-правил, то есть процедур, применяемых к элементам БД в качестве ограничения целостности

Сервер баз данных должен обеспечивать хранение данных и доступ рабочих станций к базе данных общего пользования
3 Плановые сроки начала и окончания работы по созданию системы
Срок начало работы по созданию ИС: 26 06 09
4 Требования к эксплуатации, техническому обслуживанию, ремонту и хранению компонентов системы
Режим эксплуатации ТС: односменный (8 часов)
4 Программное обеспечение
Для относительно быстрой разработки БД применяется пакет прикладных программ AllFusionModeller, в состав которого программы ERwin, Bpwin (IDEF0)
В свою очередь по ним производитель работ проверяет выполнение ежемесячного плана выработки

Второй этап – проблемы и недостатки в переработке информации
Принятая на обработку информация в основном своем содержании имеет более трети ненужной информации (информационный шум)

Помимо всех вышеперечисленных проблемах существует одна масштабная проблема
[Длина мм])*2′));
Запрос 2
Имя файла ? запроса: Короб_Запрос
Текст на SQL:
Вывести общую информацию из таблицы “КОРОБ”
[Развертка длина])))))) ‘;
Запрос 4
Имя файла ? запроса: Переход_Запрос
Текст на SQL:
Вывести общую информацию из таблицы “ПЕРЕХОД”
[Площадь м кв]
Данная операция вычисляет площадь заготовки “ ЛЕНТА_КРЕПЁЖ ”:
FROM ЛЕНТА_КРЕПЁЖ
WHERE (((ЛЕНТА_КРЕПЁЖ

Запрос 9
Имя файла ? запроса: Результат_Запрос
Текст на SQL:
Вывести итоговую информацию из таблицы 2
Классифицирование – это процесс распределения объектов данного множества на подмножества
8 Характеристика входной оперативной информации
Описание входной оперативной информации
В основе исчисления экономической эффективности лежит сопоставление существующего реально метода обработки данных (иначе базовый вариант) и внедряемого метода обработки (иначе проектный вариант)
)

Затраты на строительство и реконструкцию помещения определяется либо прямым счетом, либо относительно стоимости основного оборудования:

Кпм = (0,20 (0,50) Соб
;
Ррем – затраты, связанные с ремонтом оборудования (заработная плата сотрудников, осуществляющих ремонт, либо стоимость договора со сторонней организацией, выполняющей ремонт оборудования), руб
6 – Расходы на материалы после внедрения ИС

Расходы на материалы за 12 месяцев составили:
Рм = 16800,00 руб
7 – Затраты времени ведущего специалиста с использованием ИС

Примем стоимость затрат ведущего специалиста с использованием автоматизированной системы за заработную плату ведущего специалиста
: Финансы и статистика, 2005
Взгляд изнутри Москва МИСИС, 2000
Если же вы хотите расположить значки так, чтобы они находились рядом друг с другом, нужно:
Щелкнуть правой кнопкой мыши на любом свободном участке окна базы данных

Чтобы открыть любой объект в режиме Конструктора, необходимо выделить этот объект в списке и нажать кнопку Конструктор (Design)
Необходимо раскрыть список объектов данного типа, найти в нем нужный объект и перетащить его мышью в соответствующую папку на панели объектов
В противном случае попытка шифрования или дешифрования окажется неудачной