Как рассчитать площадь правильного шестиугольника
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник – многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
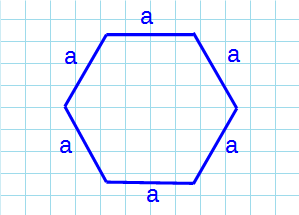
a:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через сторону:
a – сторона шестиугольника.
Через радиус описанной окружности
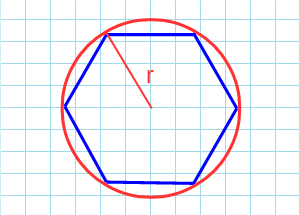
r:
Результат
Ответы:
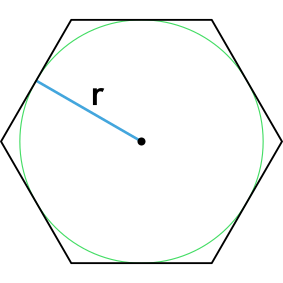
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
r – радиус описанной окружности.
Через радиус вписанной окружности
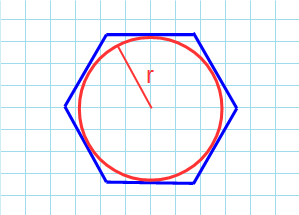
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности:
r – радиус вписанной окружности.
Калькулятор
На этой странице вы найдете калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного шестиугольника по стороне или радиусам вписанной и описанной окружностей.
Шестиугольник представляет собой многоугольник, к которого все внутренние углы равны 120 градусов, а все стороны равны между собой.
Содержание:
- калькулятор площади правильного шестиугольника
- формула площади правильного шестиугольника через длину стороны
- формула площади правильного шестиугольника через радиус вписанной окружности
- формула площади правильного шестиугольника через радиус описанной окружности
- формула площади правильного шестиугольника через периметр
- примеры задач
Формула площади правильного шестиугольника через длину стороны
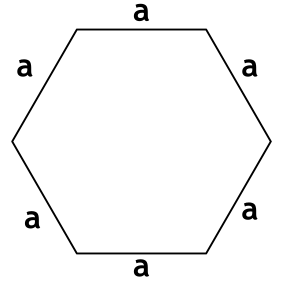
S = dfrac{3 sqrt{3} a^2}{2}
a – длина стороны шестиугольника
Формула площади правильного шестиугольника через радиус вписанной окружности
S = 2 sqrt{3}r^2
r – радиус вписанной окружности
Формула площади правильного шестиугольника через радиус описанной окружности

S = dfrac{3 sqrt{3} R^2}{2}
R – радиус описанной окружности
Формула площади правильного шестиугольника через периметр

S = dfrac{P^2 sqrt{3}}{24}
P – периметр шестиугольника
Примеры задач на нахождение площади правильного шестиугольника
Задача 1
Найдите площадь правильного шестиугольника, радиус вписанной окружности которого равен 9 см.
Решение
Исходя из того, что из условия задачи нам известен радиус вписанной окружности, мы воспользуемся формулой.
S = 2 sqrt{3}r^2 = 2 sqrt{3} cdot 9^2 = 2 sqrt{3} cdot 81 = 162 sqrt{3} : см^2 approx 280.59223 : см^2
Ответ: 162 sqrt{3} : см^2 approx 280.59223 : см^2
Проверить правильность решения нам поможет калькулятор .
Задача 2
Найдите площадь правильного шестиугольника со стороной равной 1 см.
Решение
Для этой задачи нам подойдет формула.
S = dfrac{3 sqrt{3} a^2}{2} = dfrac{3 sqrt{3} cdot 1^2}{2} = dfrac{3 sqrt{3} cdot 1}{2} = dfrac{3 sqrt{3}}{2} : см^2 approx 2.59808 : см^2
Ответ: dfrac{3 sqrt{3}}{2} : см^2 approx 2.59808 : см^2
Проверим ответ .
Правильный шестиугольник: свойства, формулы, площадь
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.

Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.

Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где
— сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольника.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
.

Радиус такой окружности равен .
Ответ: .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Ответ: .
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Правильный шестиугольник: свойства, формулы, площадь» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 февраля 2022 года; проверки требуют 2 правки.
| Шестиугольник | |
|---|---|
 Правильный шестиугольник |
|
| Тип | Правильный многоугольник |
| Рёбра | 6 |
| Символ Шлефли | {6}, t{3} |
| Диаграмма Коксетера — Дынкина |
|
| Вид симметрии | Диэдрическая группа (D6) |
| Площадь |
   |
| Внутренний угол | 120° |
| Свойства | |
| выпуклый, вписанный, Равносторонний, равноугольный[en], изотоксальный | |
Правильный шестиугольник (или гексагон от греч. εξάγωνο) — правильный многоугольник с шестью сторонами.
Свойства[править | править код]
Построение[править | править код]
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.

Правильный шестиугольник в природе, технике и культуре[править | править код]
- Пчелиные соты показывают разбиение плоскости на правильные шестиугольники.
- Некоторые сложные молекулы углерода (напр., графит) имеют гексагональную кристаллическую решётку.
- Гигантский гексагон — атмосферное явление на Сатурне.
- Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
- Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
- Гексаграмма — шестиконечная звезда, образованная двумя правильными треугольниками. Под названием звезда Давида она является символом иудаизма.
- Гексагоном[fr] иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.
Примечания[править | править код]
- ↑ А. М. Райгородский. Проблема Борсука. — М.: Издательство МЦНМО, 2006. — С. 9. — 56 с. — (Библиотека „Математическое просвещение“). — ISBN ISBN 5-94057-249-9.
См. также[править | править код]
- Шестиугольник
- Упаковка кругов на плоскости
Ссылки[править | править код]
- Шестиугольный мир (ЖЖ-сообщество)
Загрузить PDF
Загрузить PDF
Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников. Есть несколько способов найти площадь шестиугольника, в зависимости от того, имеете ли вы дело с правильным или неправильным шестиугольником. Из этой статьи вы узнаете, как именно находить площадь этой фигуры.
-

1
Запишите формулу. Так как правильный шестиугольник состоит из 6 равносторонних треугольников, то формула образована из формулы нахождения площади равностороннего треугольника: Площадь = (3√3 s2)/ 2 где s — длина стороны правильного шестиугольника.[1]
-

2
Определите длину одной стороны. Если известна длина стороны, то просто запишите ее. В нашем случае длина стороны — 9 см. Если длина стороны неизвестна, но известен периметр или апофема (высота одного из шести равносторонних треугольников, перпендикулярная стороне), то можно найти и длину стороны. Вот, как это делается:
- Если известен периметр, то просто разделите его на 6 и получите длину стороны. Если, например, периметр — 54 см, то, разделив 54 на 6, мы получим 9 см, длину стороны.[2]
- Если известна только апофема, то длину стороны можно вычислить, подставив апофему в формулу a = x√3 и затем умножив ответ на 2. Это делается потому, что апофема представляет собой сторону x√3 образуемого ей треугольника с углами 30-60-90 градусов. Если, например, апофема — 10√3, то x — 10 и длина стороны будет равна 10 * 2 или 20.
- Если известен периметр, то просто разделите его на 6 и получите длину стороны. Если, например, периметр — 54 см, то, разделив 54 на 6, мы получим 9 см, длину стороны.[2]
-

3
Подставьте значение длины стороны в формулу. Просто подставляем 9 в изначальную формулу. Получаем: площадь = (3√3 x 92)/2
-

4
Упростите ответ. Решите уравнение и запишите ответ. Ответ должен быть указан в квадратных единицах, ведь мы имеем дело с площадью. Вот, как это делается:
- (3√3 x 92)/2 =
- (3√3 x 81)/2 =
- (243√3)/2 =
- 420.8/2 =
- 210.4 см2
Реклама
-

1
Запишите формулу. Площадь = 1/2 x периметр x апофему.[3]
-

2
Запишите апофему. Скажем, она равна 5√3 см.
-

3
Используйте апофему для нахождения периметра. Апофема перпендикулярна стороне шестиугольника и создает треугольник с углами 30-60-90. Стороны такого треугольника соответствуют пропорции x-x√3-2x, где сторона короткой стороны, лежащей напротив угла в 30 градусов, представлена x, длина длинной стороны, лежащей напротив угла в 60 градусов, представлена x√3, а гипотенуза представлена 2x.[4]
- Апофема — сторона, представленная x√3. Таким образом, подставляем апофему в формулу a = x√3 и решаем. Если, например, длина апофемы — 5√3, то подставляем это число в формулу и получаем 5√3 см = x√3, или x = 5 см.
- Решая через x, мы нашли длину короткой стороны треугольника — 5 см. Эта длина представляет собой половину длины стороны шестиугольника. Умножив 5 на 2, мы получаем 10 см, длину стороны.
- Подсчитав, что длина стороны равна 10, умножаем это число на 6 и получаем периметр шестиугольника. 10 см х 6 = 60 см.
-

4
Подставьте все известные данные в формулу. Сложнее всего найти периметр. Теперь надо лишь подставить апофему и периметр в формулу и решить:
- Площадь = 1/2 x периметр x апофему
- Площадь = 1/2 x 60 см x 5√3 см
-

5
Упрощайте ответ до тех пор, пока не избавитесь от квадратных корней. Окончательный ответ укажите в квадратных единицах.
- 1/2 x 60 см x 5√3 см =
- 30 x 5√3 см =
- 150√3 см =
- 259. 8 см2
Реклама
-

1
Запишите координаты всех вершин по осям x и y. Если известны вершины шестиугольника, то первым делом надо начертить таблицу с двумя колонками и семью рядами. Каждый ряд будет назван по названию по одной из шести точек (точка А, точка В, точка С и так далее), каждая колонка будет названа по осям x или у, соответствующим координатам точек по этим осям. Запишите координаты точки А по осям x и у справа от точки, координаты точки В — справа от точки В и так далее. Внизу повторно укажите координаты первой точки. Для примера скажем, что мы имеем дело со следующими точками, в формате (x, у):[5]
- A: (4, 10)
- B: (9, 7)
- C: (11, 2)
- D: (2, 2)
- E: (1, 5)
- F: (4, 7)
- A (снова): (4, 10)
-

2
Умножьте координаты каждой точки по оси x на координаты по оси у следующей точки. Это можно представить себе так: мы проводим диагональ вниз и вправо от каждой координаты по оси x. Запишем результаты справа от таблицы. Затем сложим их.
- 4 x 7 = 28
- 9 x 2 = 18
- 11 x 2 = 22
- 2 x 5 = 10
- 1 x 7 = 7
- 4 x 10 = 40
- 28 + 18 + 22 + 10 + 7 + 40 = 125
-

3
Умножьте координаты каждой точки по оси у на координаты по оси x следующей точки. Это можно представить себе так: мы проводим диагональ вниз и влево от каждой координаты по оси у. Перемножив все координаты, складываем результаты.
- 10 x 9 = 90
- 7 x 11 = 77
- 2 x 2 = 4
- 2 x 1 = 2
- 5 x 4 = 20
- 7 x 4 = 28
- 90 + 77 + 4 + 2 + 20 + 28 = 221
-

4
Вычтите из первой суммы координат вторую сумму координат. Вычитаем 221 из 125 и получаем -96. Итак, ответ: 96, площадь может быть только положительной.
-

5
Разделите разность на два. Делим 96 на 2 и получаем площадь неправильного шестиугольника. Окончательный ответ: 48 квадратных единиц.
Реклама
-

1
Найдите площадь правильного шестиугольника с отсутствующим треугольником. Если вы столкнулись с правильным шестиугольником, в котором отсутствует один или более треугольников, то прежде всего нужно найти его площадь, как если бы он был целым. Потом необходимо найти площадь «отсутствующего» треугольника и вычесть ее из общей площади. В итоге вы получите площадь имеющейся фигуры.[6]
- Например, если мы выяснили, что площадь правильного треугольника — 60 см2, а площадь отсутствующего треугольника — 10 см2, то: 60 см2 – 10 см2 = 50 см2.
- Если известно, что в шестиугольнике не хватает точно одного треугольника, то его площадь можно найти, умножив общую площадь на 5/6, так как мы имеем 5 и 6 треугольников. Если не хватает двух треугольников, то умножаем на 4/6 (2/3) и так далее.
-

2
Разбейте неправильный шестиугольник на треугольники. Найдите площади треугольников и сложите их. В зависимости от имеющихся данных существует множество способов найти площадь треугольника.[7]
-

3
Найдите в неправильном шестиугольнике какие-то другие фигуры: треугольники, прямоугольники, квадраты. Найдите площади составляющих шестиугольник фигур и сложите их.[8]
- Один из видов неправильного шестиугольника состоит из двух параллелограммов. Для нахождения их площадей просто перемножьте основания на высоты и затем сложите их площади.
Реклама
Об этой статье
Эту страницу просматривали 128 301 раз.
