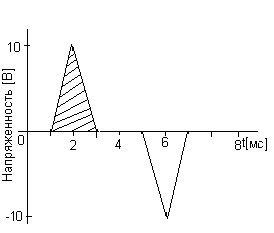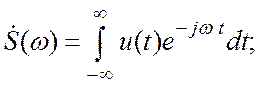 (3.5)
(3.5)
Это так называемое прямое преобразование Фурье. Зная ![]() , можно найти исходный сигнал:
, можно найти исходный сигнал:
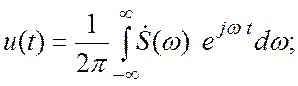 (3.6)
(3.6)
Формула (4.6) носит название обратного преобразования
Фурье.
Преобразования (3.5) и (3.6) играют фундаментальную роль
в теории сигналов. Функция ![]() называется спектральной
называется спектральной
плотностью сигнала. В литературе ![]() называют
называют
также спектральной функцией сигнала. Спектральную функцию (3.5) можно
представить в показательной форме:
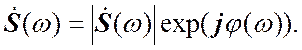 (3.7)
(3.7)
Здесь
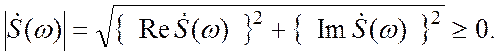
есть амплитудная спектральная функция (часто, несмотря на
неточность термина, говорят «амплитудный спектр»), а
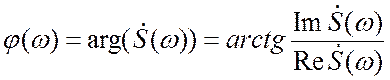 (3.8)
(3.8)
– есть фазовая спектральная функция («фазовый спектр»). Амплитудный
спектр 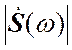 является четной, а фазовый спектр
является четной, а фазовый спектр ![]() нечетной функциями
нечетной функциями ![]() .
.
Принимая это во внимание и подставляя (3.7) в (3.6), получим соотношение
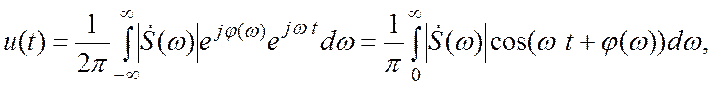
![]()
иллюстрирующее «физический смысл» спектральной функции:
сигнал ![]() представляется в виде суммы бесконечно
представляется в виде суммы бесконечно
большого числа гармонических составляющих с бесконечно малыми амплитудами 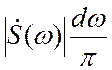 , непрерывно заполняющих интервал частот от
, непрерывно заполняющих интервал частот от
нуля до![]() . Начальные фазы этих составляющих заданы
. Начальные фазы этих составляющих заданы
функцией ![]() , а частотная зависимость «плотности»
, а частотная зависимость «плотности»
бесконечно малых амплитуд описывается функцией 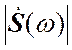 .
.
Размерность спектральной функции ![]() есть
есть
размерность сигнала, умноженная на время; так что, если размерность ![]() – вольты, то
– вольты, то 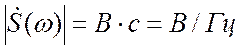 .
.
Поскольку преобразование Фурье – одно из фундаментальных
понятий теории сигналов, подробно рассмотрим его свойства.
Свойства
преобразований Фурье.
1.«Площадь» сигнала. Положив в соотношении (3.5) ![]() , получим
, получим
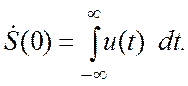 (3.9)
(3.9)
Значение ![]() численно равно
численно равно
«площади» сигнала в системе координат «время—сигнал».
2. Спектральная плотность суммы сигналов (линейность
преобразования Фурье). Пусть ![]() – сигналы со
– сигналы со
спектральными функциями ![]() , соответственно. Тогда
, соответственно. Тогда
сигналу ![]() соответствует преобразование Фурье в виде:
соответствует преобразование Фурье в виде:
![]() (3.10)
(3.10)
Доказательство предоставляется читателю сделать
самостоятельно.
3. Сдвиг сигнала во времени (теорема запаздывания).
Пусть сигналу ![]() соответствует спектральная
соответствует спектральная
функция ![]() . Найдем преобразование Фурье сдвинутого во
. Найдем преобразование Фурье сдвинутого во
времени сигнала ![]() :
:
![]() =
=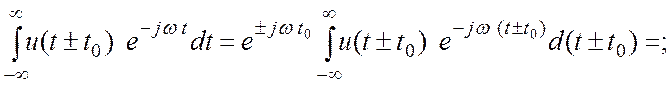
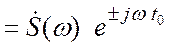 (3.11)
(3.11)
При сдвиге сигнала на временной интервал ![]() амплитудный спектр сигнала не изменяется,
амплитудный спектр сигнала не изменяется,
в фазовом спектре сигнала появляется дополнительная компонента ![]() . Множитель
. Множитель ![]() называют
называют
оператором задержки сигнала.
Пример. Спектральная функция задержанного, т. е.
сдвинутого по оси абсцисс на время τu/2 видеоимпульса
(исходный график несдвинутого сигнала см. Рис.1.4 Приложения 1):
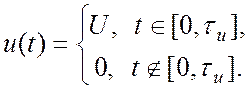
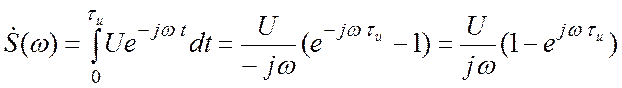
В скобках единицу представим как ![]()
![]() , второй член представим как произведение
, второй член представим как произведение
двух экспонент с половинным показателем, тогда приходим к выражению:
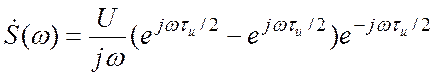
Это выражение домножим и разделим на ![]() , в числителе получаем формулу Эйлера.
, в числителе получаем формулу Эйлера.
Окончательно:
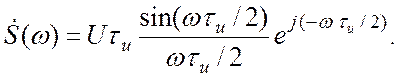 (3.12)
(3.12)
что соответствует формуле (3.11) –. спектральная функция
прямоугольного импульса домножается на экспоненту ![]() , отражающую сдвиг импульса на
, отражающую сдвиг импульса на ![]() .
.
Изменение масштаба оси времени. Найдем
преобразование Фурье для сигнала с измененным по времени масштабом ![]() :
:
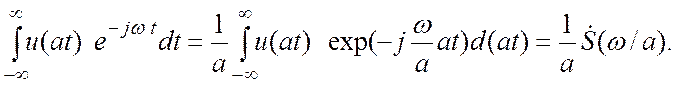
При ![]() аналогичным образом получим
аналогичным образом получим
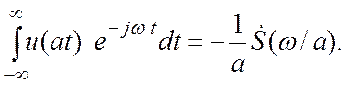
Объединение обоих случаев дает формулу
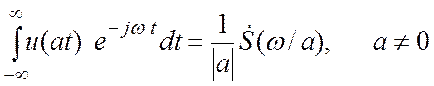
Сжатию (растяжению) сигнала во времени отвечает растяжение
(сжатие) спектральной функции по оси частот.
Дифференцирование сигнала (спектральная функция
производной).
Пусть сигналу ![]() соответствует
соответствует
спектральная функция![]() . Будем искать спектральную
. Будем искать спектральную
функцию сигнала![]() . Воспользуемся обратным
. Воспользуемся обратным
преобразованием Фурье:
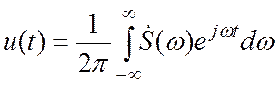
и продифференцируем по времени левую и правую часть этого
выражения. Получим:
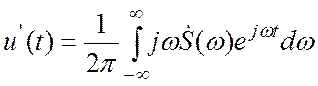 (3.13)
(3.13)
Спектральная плотность сигналов
Пусть сигнал s(t) задан в виде непериодической функции, причем он существует только на интервале (t1 ,t2) (пример — одиночный импульс). Выберем произвольный отрезок времени T, включающий в себя интервал (t1 ,t2) (см. рис.1).

Обозначим периодический сигнал, полученный из s(t), в виде  (t). Тогда для него можно записать ряд Фурье
(t). Тогда для него можно записать ряд Фурье

Для того, чтобы перейти к функции s(t) следует в выражении  (t) устремить период к бесконечности. При этом число гармонических составляющих с частотами w =n2p /T будет бесконечно велико, расстояние между ними будет стремиться к нулю ( к бесконечно малой величине:
(t) устремить период к бесконечности. При этом число гармонических составляющих с частотами w =n2p /T будет бесконечно велико, расстояние между ними будет стремиться к нулю ( к бесконечно малой величине:

амплитуды составляющих также будут бесконечно малы. Поэтому говорить о спектре такого сигнала уже нельзя,т.к.спектр становится сплошным.
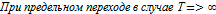 имеем:
имеем:

Внутренний интеграл является функцией частоты. Его называют спектральной плотностью сигнала, или частотной характеристикой сигнала и обозначают  т.е.
т.е.

Пределы интегрирования можно для общности поставить бесконечными, так как все равно там, где s(t) равна нулю, и интеграл равен нулю.
Выражение для спектральной плотности называют прямым преобразованием Фурье. Обратное преобразование Фурье определяет временную функцию сигнала по его спектральной плотности

рямое (*) и обратное (**) преобразования Фурье вместе называют парой преобразований Фурье. Модуль спектральной плотности 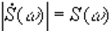
определяет амплитудно-частотную характеристику (АЧХ) сигнала, а ее аргумент  называют фазо-частотной характеристикой (ФЧХ) сигнала. АЧХ сигнала является четной функцией, а ФЧХ — нечетной.
называют фазо-частотной характеристикой (ФЧХ) сигнала. АЧХ сигнала является четной функцией, а ФЧХ — нечетной.
Смысл модуля S(w ) определяется как амплитуда сигнала (тока или напряжения), приходящаяся на 1 Гц в бесконечно узкой полосе частот, которая включает в себя рассматриваемую частоту w . Его размерность — [сигнал/частота].
Энергетический спектр сигнала. Если функция s(t) имеет фурье-плотность мощности сигнала (спектральная плотность энергии сигнала) определяется выражением:
Спектр мощности W()-вещественная неотрицательная четная функция, которую обычно называют энергетическим спектром. Спектр мощности, как квадрат модуля спектральной плотности сигнала, не содержит фазовой информации о его частотных составляющих, а, следовательно, восстановление сигнала по спектру мощности невозможно. Это означает также, что сигналы с различными фазовыми характеристиками могут иметь одинаковые спектры мощности. В частности, сдвиг сигнала не отражается на его спектре мощности. Последнее позволяет получить выражение для энергетического спектра непосредственно из выражений (5.2.7). В пределе, для одинаковых сигналов u(t) и v(t) при сдвиге t  0, мнимая часть спектра Wuv () стремится к нулевым значениям, а реальная часть — к значениям модуля спектра. При полном временном совмещении сигналов имеем:
0, мнимая часть спектра Wuv () стремится к нулевым значениям, а реальная часть — к значениям модуля спектра. При полном временном совмещении сигналов имеем:

т.е. энергия сигнала равна интегралу квадрата модуля его частотного спектра — сумме энергии его частотных составляющих, и всегда является вещественной величиной.
Для произвольного сигнала s(t) равенство

обычно называют равенством Парсеваля (в математике – теоремой Планшереля, в физике – формулой Релея). Равенство очевидно, так как координатное и частотное представления по существу только разные математические отображения одного и того же сигнала. Аналогично для энергии взаимодействия двух сигналов:
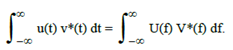
Из равенства Парсеваля следует инвариантность скалярного произведения сигналов и нормы относительно преобразования Фурье:
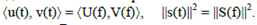
В целом ряде чисто практических задач регистрации и передачи сигналов энергетический спектр сигнала имеет весьма существенное значение. Периодические сигналы переводятся в спектральную область в виде рядов Фурье. Запишем периодический сигнал с периодом Т в виде ряда Фурье в комплексной форме:

Интервал 0-Т содержит целое число периодов всех подынтегральных экспонент, и равен нулю, за исключением экспоненты при k = -m, для которой интеграл равен Т. Соответственно, средняя мощность периодического сигнала равна сумме квадратов модулей коэффициентов его ряда Фурье:

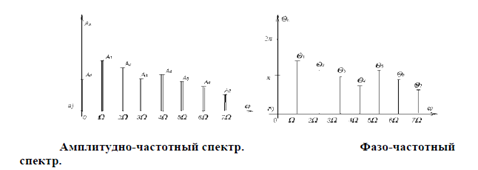
Энергетический спектр сигнала– это распределение энергии базисных сигналов, которые составляют негармонический сигнал, на оси частот. Математически энергетический спектр сигнала равен квадрату модуля спектральной функции:

Соответственно амплитудно-частотный спектр показывает множество амплитуд составляющих базисных сигналов на частотной оси, а фазо-частотный – множество фаз
Модуль спектральной функции часто называют амплитудным спектром, а ее аргумент – фазовым спектром.
Кроме того, существует и обратное преобразование Фурье, позволяющее восстановить исходный сигнал, зная его спектральную функцию:


Например, возьмем прямогульный импульс:

Еще один пример спектров:
Частота Найквиста, теорема Котельникова.
Частота Найквиста — в цифровой обработке сигналов частота, равная половине частоты дискретизации. Названа в честь Гарри Найквиста. Из теоремы Котельникова следует, что при дискретизации аналогового сигнала потерь информации не будет только в том случае, если спектр (спектральная плотность)(наивысшая частота полезного сигнала) сигнала равен или ниже частоты Найквиста. В противном случае при восстановлении аналогового сигнала будет иметь место наложение спектральных «хвостов» (подмена частот, маскировка частот), и форма восстановленного сигнала будет искажена. Если спектр сигнала не имеет составляющих выше частоты Найквиста, то он может быть (теоретически) продискретизирован и затем восстановлен без искажений. Фактически «оцифровка» сигнала (превращение аналогового сигнала в цифровой) сопряжена с квантованием отсчѐтов — каждый отсчѐт записывается в виде цифрового кода конечной разрядности, в результате чего к отсчетам добавляются ошибки квантования (округления), при определенных условиях рассматриваемые как «шум квантования».
Реальные сигналы конечной длительности всегда имеют бесконечно широкий спектр, более или менее быстро убывающий с ростом частоты. Поэтому дискретизация сигналов всегда приводит к потерям информации (искажению формы сигнала при дискретизации—восстановлении), как бы ни была высока частота дискретизации. При выбранной частоте дискретизации искажение можно уменьшить, если обеспечить подавление спектральных составляющих аналогового сигнала (до дискретизации), лежащих выше частоты Найквиста, для чего требуется фильтр очень высокого порядка, чтобы избежать наложения «хвостов». Практическая реализация такого фильтра весьма сложна, так как амплитудно-частотные характеристики фильтров имеют не прямоугольную, а гладкую форму, и образуется некоторая переходная полоса частот между полосой пропускания и полосой подавления. Поэтому частоту дискретизации выбирают с запасом, к примеру, в аудио компакт-дисках используется частота дискретизации 44100 Герц, в то время как высшей частотой в спектре звуковых сигналов считается частота 20000 Гц. Запас по частоте Найквиста в 44100 / 2 — 20000 = 2050 Гц позволяет избежать подмены частот при использовании реализуемого фильтра невысокого порядка.
Теорема Котельникова
Для того, чтобы восстановить исходный непрерывный сигнал из дискретизированного с малыми искажениями (погрешностями), необходимо рационально выбрать шаг дискретизации. Поэтому при преобразовании аналогового сигнала в дискретный обязательно возникает вопрос о величине шага дискретизации  Интуитивно нетрудно понять следующую идею. Если аналоговый сигнал обладает низкочастотным спектром, ограниченным некоторой верхней частотой Fe, (т.е. функция u(t) имеет вид плавно изменяющейся кривой, без резких изменений амплитуды), то вряд ли на некотором небольшом временном интервале дискретизации
Интуитивно нетрудно понять следующую идею. Если аналоговый сигнал обладает низкочастотным спектром, ограниченным некоторой верхней частотой Fe, (т.е. функция u(t) имеет вид плавно изменяющейся кривой, без резких изменений амплитуды), то вряд ли на некотором небольшом временном интервале дискретизации  эта функция может существенно изменяться по амплитуде. Совершенно очевидно, что точность восстановления аналогового сигнала по последовательности его отсчетов зависит от величины интервала дискретизации
эта функция может существенно изменяться по амплитуде. Совершенно очевидно, что точность восстановления аналогового сигнала по последовательности его отсчетов зависит от величины интервала дискретизации  Чем он короче, тем меньше будет отличаться функция u(t) от плавной кривой, проходящей через точки отсчетов. Однако с уменьшением интервала дискретизации
Чем он короче, тем меньше будет отличаться функция u(t) от плавной кривой, проходящей через точки отсчетов. Однако с уменьшением интервала дискретизации  существенно возрастает сложность и объем обрабатывающей аппаратуры. При достаточно большом интервале дискретизации
существенно возрастает сложность и объем обрабатывающей аппаратуры. При достаточно большом интервале дискретизации  возрастает вероятность искажения или потери информации при восстановлении аналогового сигнала. Оптимальная величина интервала дискретизации устанавливается теоремой Котельникова (другие названия — теорема отсчетов, теорема К. Шеннона, теорема X. Найквиста: впервые теорема была открыта в математике О. Коши, а затем описана повторно Д. Карсоном и Р. Хартли), доказанной им в 1933 г. Теорема В. А. Котельникова имеет важное теоретическое и практическое значение: дает возможность правильно осуществить дискретизацию аналогового сигнала и определяет оптимальный способ его восстановления на приемном конце по отсчетным значениям.
возрастает вероятность искажения или потери информации при восстановлении аналогового сигнала. Оптимальная величина интервала дискретизации устанавливается теоремой Котельникова (другие названия — теорема отсчетов, теорема К. Шеннона, теорема X. Найквиста: впервые теорема была открыта в математике О. Коши, а затем описана повторно Д. Карсоном и Р. Хартли), доказанной им в 1933 г. Теорема В. А. Котельникова имеет важное теоретическое и практическое значение: дает возможность правильно осуществить дискретизацию аналогового сигнала и определяет оптимальный способ его восстановления на приемном конце по отсчетным значениям.
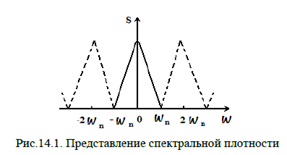
Согласно одной из наиболее известных и простых интерпретаций теоремы Котельникова, произвольный сигнал u(t), спектр которого ограничен некоторой частотой Fe может — быть полностью восстановлен по последовательности своих отсчетных значений, следующих с интервалом времени

Интервал дискретизации  и частоту Fe (1) в радиотехнике часто называют соответственно интервалом и частотой Найквиста. Аналитически теорема Котельникова представляется рядом
и частоту Fe (1) в радиотехнике часто называют соответственно интервалом и частотой Найквиста. Аналитически теорема Котельникова представляется рядом 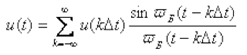
где k — номер отсчета; 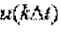 — значение сигнала в точках отсчета
— значение сигнала в точках отсчета  — верхняя частота спектра сигнала.
— верхняя частота спектра сигнала.
Частотное представление дискретных сигналов.
Большинство сигналов можно представить в виде ряда Фурье:


Преобразование Лапласа
Преобразование Лапласа — интегральное преобразование, связывающее функцию  комплексного переменного (изображение) с функцией
комплексного переменного (изображение) с функцией  вещественного переменного (оригинал).
вещественного переменного (оригинал).

Свойства преобразования Лапласса:
1. Линейность. Для любых комплексных постоянных a и b

Ортогональное преобразование дискретных сигналов (преобразование Фурье)
Как известно, наряду с описанием сигналов посредством задания их мгновенных значений в виде формул, определяющих зависимости от времени x(t). (т.е. во временной области, т.к. аргумент — время t), существует и другой способ — спектральное представление сигналов, при котором сигналы задаются спектрами.
Переход от временного представления сигнала к спектральному и обратно называются ортогональными преобразованиями.
Каждому виду сигнала x(t) соответствует свой спектр X(jw), связанный с x(t) преобразованием Фурье:

Преобразование Фурье обладает следующими свойствами:


Преобразование Адамара.
Преобразование Адамара, или преобразование Уолша-Адамара позволяет раскладывать сигналы произвольной формы в обобщенный ряд Фурье. Это достигается за счет применения ортонормированных базисов. Любую матрицу Адамара порядка 2N можно рекурсивно получить из N так:
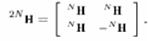
В качестве примера рассчитаем дискретное преобразование Уолша-Адамара последовательности (1, 2, 0, 3). Матрица адамара порядка 4х4 равна

Следовательно дискретное преобразование Уолша-Адамара вышеприведенной полседовательности будет выглядеть следующим образом:

Быстрое преобразование Адамара.
Пусть имеется вектора . Его преобразование Адамара есть вектор  Вектор
Вектор  называется спектром Адамара исходного вектора. Обратное преобразование
называется спектром Адамара исходного вектора. Обратное преобразование  можно рассматривать как разложение вектора
можно рассматривать как разложение вектора  по столбцам
по столбцам  при этом число перемен знаков в соответствующем столбце рассматривается как аналог частоты. Разобьем вектор
при этом число перемен знаков в соответствующем столбце рассматривается как аналог частоты. Разобьем вектор  представив его в виде блоков длины
представив его в виде блоков длины  Имеем
Имеем

Для вычисления блоков можем применить аналогичную формулу. Таким образом реализуется быстрое преобразование Адамара
Об авторегрессионном оценивании спектральной плотности стационарного сигнала
Методы спектрального оценивания стационарных случайных процессов, основанные на быстром преобразовании Фурье (БПФ), хорошо известны и широко применяются в инженерной практике. К их недостаткам следует отнести, в частности, высокую дисперсию (низкую точность) оценки при недостаточно длительном интервале наблюдения за процессом, что визуально обычно проявляется в сильной «изрезанности» графика спектральной плотности мощности(СПМ). Одним из альтернативных методов спектрального оценивания является авторегрессионный метод, рассмотренный на примере ниже, который в инженерной практике известен гораздо меньше. Метод во многих случаях позволяет сравнительно просто получить гораздо более качественную оценку СПМ (рис.1), а иногда и более глубокие сведения об исследуемом случайном процессе.

Рис.1 Классическая и авторегрессионная оценка СПМ «короткого» процесса
Для демонстрационных целей был синтезирован дискретно-временной сигнал (последовательность) x[i]. Сигнал смоделирован при помощи ARMA-модели (цифрового фильтра), имитирующей свойства механической системы (1) — перемещение материальной точки x(t) в «одномассовом» осцилляторе с параметрами m=1 кг, c= 100 Н/м, k=2,5 кг/с, и силовым возмущением — гауссовым «белым»(с учетом дискретизации) шумом f(t) с дисперсией 1 Н 2 , интервал дискретизации по времени Δt=0,12 с.
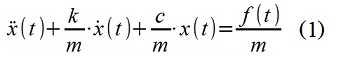
Построена модель (2). Способ построения модели уже рассматривался ранее здесь .
x[i] — 0.6388· x[i-1] + 0.7408· x[i-2] = 0.009667·f[i-1] (2)
С помощью (2) синтезирована последовательность в 50 тыс. отсчетов, для чего использован генератор нормально-распределенной случайной величины randn( ) общеизвестной программной среды.
После завершения моделирования процесса x[i], количественные параметры модели (2) предполагаются неизвестными — для исследования доступен только сам процесс и, в какой-то мере, сведения о свойствах модели в самых общих чертах.
Было проведено спектральное оценивание 50000-точечной последовательности методом Уэлча, размер сегмента принят равным 256 отсчетам, применено окно Хэмминга и 60% перекрытие сегментов. Среднеквадратичное отклонение такой оценки, исходя из того, что последовательность имеет длину около 200 неперекрывающихся сегментов, может быть примерно оценено, как
Далее, предполагая, что в реальных условиях в эксперименте для исследования доступна гораздо менее длинная последовательность, проведены исследования только по первым 500 отсчетам этого сигнала.
Получена оценка методом Уэлча с теми же параметрами. СКО такой оценки
70%, заметна очень сильная «изрезанность» графика (рис.2).

Рис.2 Оценивание СПМ «длинного» и «короткого» процессов классическими методом
Исходя из того, что примерный вид функции (графика) СПМ процесса нам известен (например, исходя из известной физической природы процесса — одномассовый осциллятор под белым шумом, либо из оценивания аналогичных процессов, для которых доступны более длинные реализации), принято решение об оценивании с помощью модели авторегрессии второго порядка (AR(2), или =ARMA(2,0)).
Определение порядка модели — весьма важный момент, ошибка в порядке может повлечь очень грубые ошибки в результатах оценивания. Существуют методы, здесь пока не рассматриваемые, помогающие в определении порядка модели на основании только самого анализируемого процесса.
Оценивание параметров модели поизведено с помощью известных уравнений Юла-Уолкера для авторегрессионного процесса (несущественно модифицированных с целью некоторого упрощения структуры скрипта ):
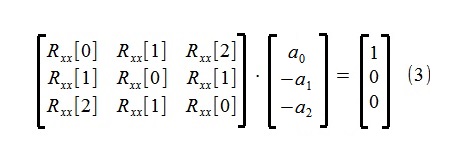
Как видно из уравнений, для определения параметров понадобятся только три первых члена авторегрессионной последовательности Rxx[0], Rxx[1], Rxx[2], которые и были оценены по исходной 500-точечной последовательности x[i] корелограммным методом, СКО такой оценки
(Кстати, видно, что «минусы» перед a1, a2 2и т.д, крайне неудобны. Они и появились-то из-за преимущественно «предсказательного» использования ARMA-моделей в экономике, в более ранних «инженерных» источниках их нет. Уже сомневаюсь, что надо было здесь использовать такое понимание AR-коэффициентов.)
Корреляционная матрица в (3) на практике всегда имеет строгое диагональное преобладание | Rxx[0] | >| Rxx[i] |, в том числе по причине присутствия шумов наблюдения, вследствие чего трудностей с ее обращением (нахождением решения(3)) не возникает.
(Для пояснения вопроса о величине статистической ошибки моделирования интересно упомянуть, например, оценку Rxx[0] =2.2606e-04 м 2 , полученную по 500 отсчетам, в сравнении с полученными корелограммной оценкой дисперсии по 50000 отсчетам, = 2.4238e-04 м 2 и оценкой по подынтегральной площади СПМ, полученной методом Уэлча по 50000 отсчетам (рис.2), = 2.4232e-04 м 2 )
После подстановки найденных оценок Rxx[i] имеем:

Определены следующие параметры модели a0=11325.9; a1=7090.1; a2=-8411.5; Как видно из (3), дисперсией гипотетического вхоящего белого шума здесь задались =1, определив вместо нее коэффициент усиления a0. Авторегрессионная оценка СПМ построена путем преобразования Фурье над последовательностью коэффициентов a0, a1, a2:
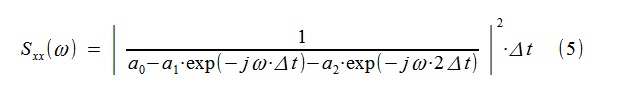
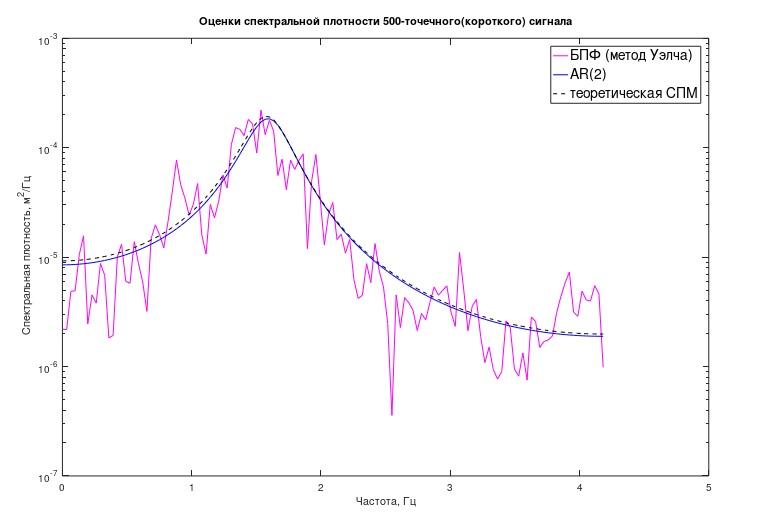
Рис.3 Классическая и авторегрессионная оценка СПМ «короткого» процесса
Таким же образом, по выражению, аналогичному (5), был ранее построен и «теоретический» график СПМ, только коэффициенты модели там, естественно, были взяты иные (из (2)).
Из графика видно, что AR-оценка СПМ получилась весьма близка к теоретически ожидаемой. Помимо графика, есть возможность попытаться оценить некоторые аналитические характеристики процесса и связанной с ним механической системы. В данном случае это «полюса» модели, численно характеризующие частоты «резонансных» пиков модели и связанные с ними «добротности».
Из (5) находим соотношение для поиска разрывов передаточной функции нашей модели, используя преобразование Лапласа (заменяя jω на λ=-ε+ jω):
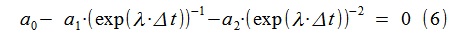
Для полученной AR- модели таким способом вычислены λ1,2= -1.5427 ± j· 10.1514, что весьма близко к исходной модели, использованной для генерации процесса
λ1,2теор=-1.2500 ± j · 9.9216 (т.е положения резонансного пика соответственно, 1,615 Гц (в теории) и 1,579 Гц (определено)).
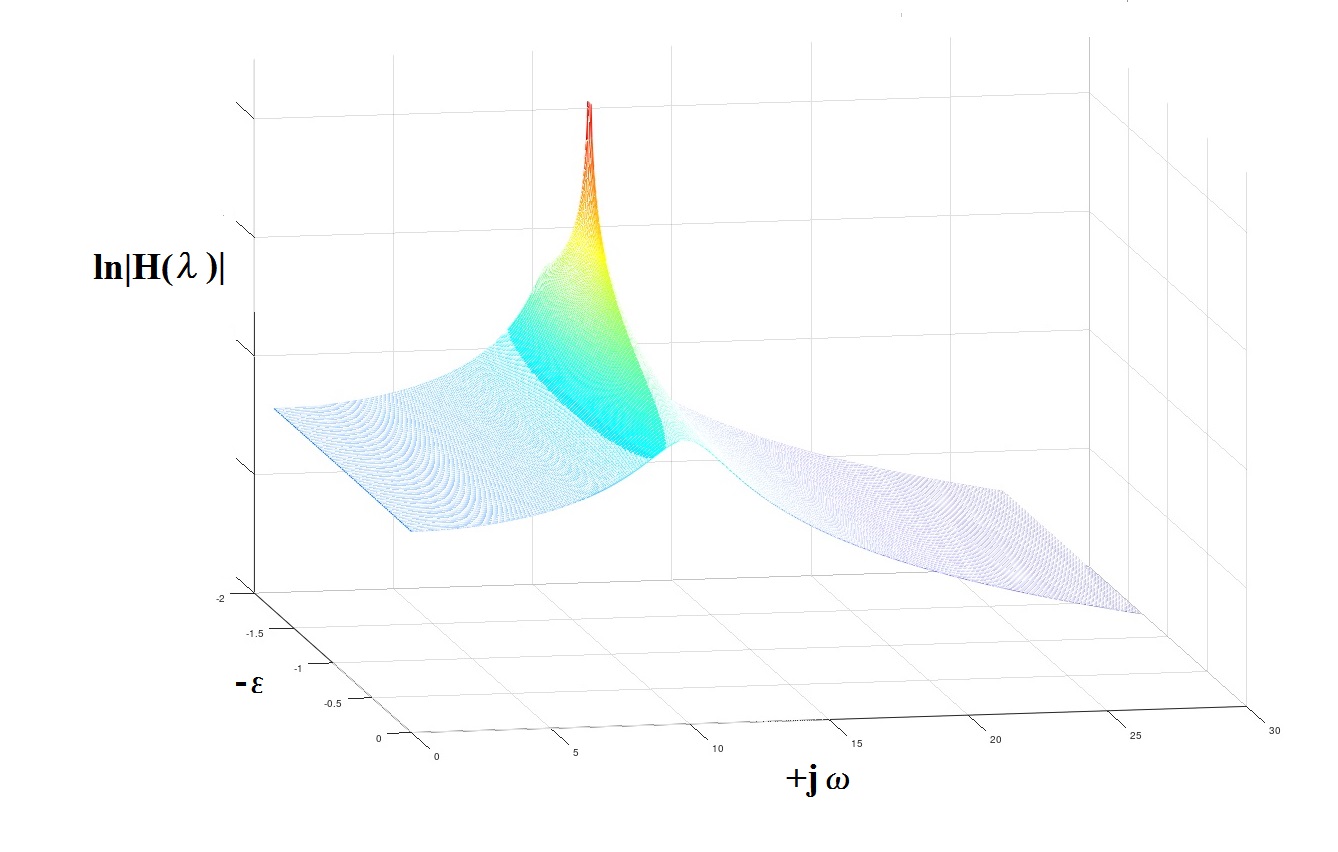
Рис.4 О понятии «полюсов»
Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие , страница 6
Это так называемое прямое преобразование Фурье. Зная , можно найти исходный сигнал:
Формула (4.6) носит название обратного преобразования Фурье.
Преобразования (3.5) и (3.6) играют фундаментальную роль в теории сигналов. Функция называется спектральной плотностью сигнала. В литературе называют также спектральной функцией сигнала. Спектральную функцию (3.5) можно представить в показательной форме:
есть амплитудная спектральная функция (часто, несмотря на неточность термина, говорят «амплитудный спектр»), а
– есть фазовая спектральная функция («фазовый спектр»). Амплитудный спектр является четной, а фазовый спектр нечетной функциями . Принимая это во внимание и подставляя (3.7) в (3.6), получим соотношение
иллюстрирующее «физический смысл» спектральной функции: сигнал представляется в виде суммы бесконечно большого числа гармонических составляющих с бесконечно малыми амплитудами , непрерывно заполняющих интервал частот от нуля до . Начальные фазы этих составляющих заданы функцией , а частотная зависимость «плотности» бесконечно малых амплитуд описывается функцией .
Размерность спектральной функции есть размерность сигнала, умноженная на время; так что, если размерность — вольты, то .
Поскольку преобразование Фурье – одно из фундаментальных понятий теории сигналов, подробно рассмотрим его свойства.
Свойства преобразований Фурье.
1.«Площадь» сигнала. Положив в соотношении (3.5) , получим
Значение численно равно «площади» сигнала в системе координат «время—сигнал».
2. Спектральная плотность суммы сигналов (линейность преобразования Фурье). Пусть – сигналы со спектральными функциями , соответственно. Тогда сигналу соответствует преобразование Фурье в виде:
Доказательство предоставляется читателю сделать самостоятельно.
3. Сдвиг сигнала во времени (теорема запаздывания). Пусть сигналу соответствует спектральная функция . Найдем преобразование Фурье сдвинутого во времени сигнала :
При сдвиге сигнала на временной интервал амплитудный спектр сигнала не изменяется, в фазовом спектре сигнала появляется дополнительная компонента . Множитель называют оператором задержки сигнала.
Пример. Спектральная функция задержанного, т. е. сдвинутого по оси абсцисс на время τu/2 видеоимпульса (исходный график несдвинутого сигнала см. Рис.1.4 Приложения 1):
В скобках единицу представим как , второй член представим как произведение двух экспонент с половинным показателем, тогда приходим к выражению:
Это выражение домножим и разделим на , в числителе получаем формулу Эйлера. Окончательно:
что соответствует формуле (3.11) –. спектральная функция прямоугольного импульса домножается на экспоненту , отражающую сдвиг импульса на .
Изменение масштаба оси времени. Найдем преобразование Фурье для сигнала с измененным по времени масштабом :
При аналогичным образом получим
Объединение обоих случаев дает формулу
Сжатию (растяжению) сигнала во времени отвечает растяжение (сжатие) спектральной функции по оси частот.
Дифференцирование сигнала (спектральная функция производной).
Пусть сигналу соответствует спектральная функция. Будем искать спектральную функцию сигнала. Воспользуемся обратным преобразованием Фурье:
и продифференцируем по времени левую и правую часть этого выражения. Получим:
Спектральные плотности некоторых сигналов
Содержание
Обнаружили ошибку?
Выделите ее мышью
и нажмите

Спектральная плотность прямоугольного импульса
Рассмотрим спектральную плотность  прямоугольного импульса
прямоугольного импульса  длительности
длительности  и амплитуды
и амплитуды  . Функция
. Функция  описывает прямоугольный импульс длительности
описывает прямоугольный импульс длительности  и единичной амплитуды:
и единичной амплитуды:

(1)
График прямоугольного импульса показан на рисунке 1а.

Рисунок 1. Спектральная плотность прямоугольного импульса
а — временно́й сигнал; б — спектральная плотность
Спектральная плотность  прямоугольного импульса
прямоугольного импульса  равна:
равна:

(2)
где  . График спектральной плотности
. График спектральной плотности  прямоугольного импульса показан на рисунке 1б.
прямоугольного импульса показан на рисунке 1б.
Приведем основные частотные свойства  .
.
Спектральная плотность треугольного импульса
Рассмотрим треугольный импульс  длительности
длительности  и амплитуды
и амплитуды  :
:

(3)
График треугольного импульса показан на рисунке 2а.

Рисунок 2. Спектральная плотность треугольного импульса
а — временно́й сигнал; б — спектральная плотность
Для рассмотрения спектральной плотности треугольного импульса мы не будем вычислять интеграл Фурье непосредственно, потому что это потребует громоздких выкладок, а воспользуемся свойством преобразования Фурье свертки двух сигналов.
Можно заметить, что треугольный импульс длительности  и амплитуды
и амплитуды  может быть представлен как результат свертки прямоугольного импульса
может быть представлен как результат свертки прямоугольного импульса  длительности
длительности  и амплитуды
и амплитуды  c самим собой, как это показано на рисунке 3.
c самим собой, как это показано на рисунке 3.

Рисунок 3. Треугольный импульс как результат
свертки прямоугольных импульсов
Обратим внимание, что один из углов  маркирован черным квадратиком для того, чтобы показать инверсию во времени сдвинутого сигнала
маркирован черным квадратиком для того, чтобы показать инверсию во времени сдвинутого сигнала  , входящего в интеграл свертки.
, входящего в интеграл свертки.
Для различного сдвига  мы будем иметь линейно нарастающую площадь (заштрихованная область) произведения
мы будем иметь линейно нарастающую площадь (заштрихованная область) произведения  сигнала
сигнала  и его сдвинутой инверсной во времени копии
и его сдвинутой инверсной во времени копии  .
.
Таким образом, мы можем применить
свойство преобразования Фурье свертки сигналов
и записать спектральную плотность треугольного импульса как квадрат спектральной плотности  прямоугольного импульса
прямоугольного импульса  длительности
длительности  и амплитуды
и амплитуды  :
:

(4)
График спектральной плотности треугольного импульса показан на рисунке 2б.
Приведем основные частотные свойства  .
.
Спектральная плотность гауссова импульса
Гауссов импульс  задается выражением:
задается выражением:

(5)
где  — амплитуда, а
— амплитуда, а  — положительный параметр, который задает ширину импульса.
— положительный параметр, который задает ширину импульса.
График гауссова импульса при различном значении  и
и  показан на рисунке 4а.
показан на рисунке 4а.

Рисунок 4. Спектральная плотность гауссова импульса
а — временно́й сигнал; б — спектральная плотность
Рассмотрим спектральную плотность гауссова импульса:

(6)
Преобразуем показатель экспоненты (6) следующим образом:

(7)
Тогда (6) с учетом (7):

(8)
Из курса математического анализа [1, стр. 401] известно, что:

(9)
Введем в выражении (8) замену переменной  , тогда
, тогда  , пределы интегрирования остаются неизменными при положительном значении
, пределы интегрирования остаются неизменными при положительном значении  . Тогда (8) можно представить как:
. Тогда (8) можно представить как:

(10)
и с учетом (9) окончательно можно записать:

(11)
Можно заметить, что временно́й гауссов импульс  имеет спектральную плотность
имеет спектральную плотность  , которая также описывается гауссовской функцией.
, которая также описывается гауссовской функцией.
График спектральной плотности гауссова импульса для различного значения параметра  показан на рисунке 4б.
показан на рисунке 4б.
C увеличением  увеличивается ширина гауссова импульса во временно́й области, и сужение спектральной плотности. При этом, убывание импульса во времени и по частоте носит экспоненциальный характер.
увеличивается ширина гауссова импульса во временно́й области, и сужение спектральной плотности. При этом, убывание импульса во времени и по частоте носит экспоненциальный характер.
Спектральная плотность экспоненциального импульса
Рассмотрим двусторонний экспоненциальный импульс  , который задается выражением:
, который задается выражением:

(12)
где  — амплитуда, а
— амплитуда, а  — положительный параметр, который определяет ширину импульса.
— положительный параметр, который определяет ширину импульса.
График двустороннего экспоненциального импульса при  и различном значении параметра
и различном значении параметра  показан на рисунке 5а.
показан на рисунке 5а.

Рисунок 5. Спектральная плотность двустороннего экспоненциального импульса
а — временно́й сигнал; б — спектральная плотность
Как можно видеть из рисунка 5а, увеличение параметра  приводит к сужению импульса во временно́й области.
приводит к сужению импульса во временно́й области.
Рассмотрим спектральную плотность  двустороннего экспоненциального импульса:
двустороннего экспоненциального импульса:

(13)
Разобьем ось времени на положительную и отрицательную полуоси, и учтем что  для отрицательной полуоси времени. Тогда (13) можно записать:
для отрицательной полуоси времени. Тогда (13) можно записать:

(14)
Объединим показатели экспонент в обоих интегралах и получим:

(15)
Таким образом, спектральная плотность двустороннего экспоненциального импульса (12) представляет собой вещественную функцию частоты, обладающую следующими свойствами.
На рисунке 5б показан вид спектральной плотности  при различном значении
при различном значении  . Можно видеть, что при увеличении параметра
. Можно видеть, что при увеличении параметра  , спектральная плотность сужается (импульс во временно́й области —расширяется).
, спектральная плотность сужается (импульс во временно́й области —расширяется).

Рисунок 6. Односторонний экспоненциальный импульс
Рассмотрим теперь односторонний экспоненциальный импульс, который получается из двустороннего при обнулении значения отрицательной полуоси времени:

(16)
График одностороннего экспоненциального импульса показан на рисунке 6 при  и различном
и различном  .
.
Спектральная плотность одностороннего экспоненциального импульса равна:

(17)
Приведем основные частотные свойства  одностороннего экспоненциального импульса:
одностороннего экспоненциального импульса:
Поскольку спектральная плотность одностороннего экспоненциального импульса является комплексной функцией частоты  , то можно представить
, то можно представить  в виде амплитудно- и фазочастотной характеристик:
в виде амплитудно- и фазочастотной характеристик:

(18)
На рисунке 7 показаны АЧХ и ФЧХ одностороннего экспоненциального импульса для различных значения параметра  .
.

Рисунок 7. АЧХ и ФЧХ одностороннего экспоненциального импульса
а — АЧХ; б — ФЧХ
Спектральная плотность функции 
Рассмотрим спектральную плотность сигнала вида  , где
, где  — параметр определяющий ширину главного лепестка функции
— параметр определяющий ширину главного лепестка функции  , как это показано на рисунке 8а.
, как это показано на рисунке 8а.

Рисунок 8. Спектральная плотность функции 
а — временно́й сигнал; б — спектральная плотность
Для получения спектральной плотности сигнала  воспользуемся
воспользуемся
свойством двойственности преобразования Фурье,
рассмотренным в
в предыдущем параграфе.
Тогда из выражения (2) можно записать:

(19)
Произведем замену переменных  и
и  , а также обозначим
, а также обозначим  , откуда
, откуда  :
:

(20)
Вынесем множитель  из под оператора преобразования Фурье, и окончательно спектральная плотность сигнала
из под оператора преобразования Фурье, и окончательно спектральная плотность сигнала  равна:
равна:

(21)
График спектральной плотности сигнала  показан на рисунке 8б.
показан на рисунке 8б.
Важным частным случаем является  , тогда
, тогда  будет иметь спектральную плотность
будет иметь спектральную плотность  , что соответствует частотной характеристике идеального фильтра нижних частот. Временно́й сигнал
, что соответствует частотной характеристике идеального фильтра нижних частот. Временно́й сигнал  определяет импульсную характеристику идеального фильтра нижних частот.
определяет импульсную характеристику идеального фильтра нижних частот.
Выводы
В данном разделе мы рассмотрели спектральные плотности некоторых непериодических сигналов: прямоугольного, треугольного, гауссова импульса,
а также одностороннего и двустороннего экспоненциальных импульсов.
Были приведены аналитические выражения для спектральных плотностей каждого из сигналов, а также их частотные свойства.
Смотри также
Представление периодических сигналов рядом Фурье
Преобразование Фурье непериодических сигналов
Свойства преобразования Фурье
Спектральные плотности некоторых сигналов
Список литературы
[1]
Кратные интегралы и ряды.
Москва, Наука, 1965, 608 c.
[2]
Баскаков, С.И.
Радиотехнические цепи и сигналы.
Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4
[3]
Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.
[4]
Bracewell R.
The Fourier Transform and Its Applications
McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6
Последнее изменение страницы: 12.05.2022 (19:42:52)
Страница создана Latex to HTML translator ver. 5.20.11.14
-
. Свойства спектров
Из преобразований Фурье следует ряд
свойств спектров. Некоторые из них без
выводов приводятся ниже. Сигнал S(t)
предполагается действительным.
Спектр несимметричного сигнала –
комплексный, эрмитово- сопряженный:
![]() .
.
(25)
Его реальная часть А()есть функция четная, а мнимаяВ()
– нечетная:
Спектр четного сигнала – действительный
и четный:
![]() (26)
(26)
Спектр нечетного сигнал – мнимый и
нечетный:
![]()
![]() (27)
(27)
Обращение сигнала во времени приводит
к обращению спектра по частоте:
![]() (28)
(28)
Значение спектра при
![]() определяется площадью сигнала:
определяется площадью сигнала:
![]() .
.
(29)
Спектр суммы сигналов равен сумме их
спектров (теорема сложения):
![]() (30)
(30)
При сдвиге сигнала на фаза его спектра изменяется на -(теорема запаздывания):
![]() (31)
(31)
При умножении сигнала на
![]() его спектр, не меняя своего вида, смещается
его спектр, не меняя своего вида, смещается
на величину![]() (теорема смещения):
(теорема смещения):
![]() .
.
(32)
Расширению сигнала во времени
соответствует сужение его спектра
(теорема расширения):
![]() .
.
(33)
При взятии производной от сигнала
его спектр умножается на
![]() (теорема о производной)
(теорема о производной)
![]() (34)
(34)
Взятие интеграла от сигнала
соответствует делению спектра на
![]() (теорема об интеграле):
(теорема об интеграле):
 (35)
(35)
Спектр произведения двух сигналов
равен свертке их спектров (теорема о
произведении сигналов):
![]() .
.
(36)
Спектр свертки двух сигналов равен
произведению их спектров (теорема о
свертке):
![]() (37)
(37)
Взаимозаменяемость частоты fи времениt (теорема
дуальности):
Если
![]() ,
,
то![]() . (38)
. (38)
-
. Спектры некоторых видеосигналов
Видеосигналамив отличие отрадиосигналовназывают сигналы без
высокочастотного заполнения. Определение
это, не являясь строгим, общепринято и
интуитивно понятно. В данной работе
изучаются спектры распространенных
видеосигналов:-импульсов,
прямоугольного, треугольного и
гауссового.
2.4.1. Дельта-сигналы
Математической моделью сигнала очень
короткой длительности является бесконечно
узкая и бесконечно высокая, но с конечной
площадью, (t)-функция
Дирака. Амплитудой-функции
называется ее площадь (реально – площадь
сигнала). Спектр(t)сплошной и для функции единичной
амплитуды, располагающейся в начале
координат (рис.5,а), он равен 1:
![]()
(t)
. (39)

S (t)
S (t)
![]()
0
t0

0

t
t
1
S
()
|
S ()
|


A



0

0


A
(t – t0)
=
–
t0
![]() а
а
б
Рис.5.
Дельта-импульсы и их спектры:
а –
единичный в начале координат; б –
смещенный на t0 с
амплитудойA
Для импульса с амплитудой A
, смещенного наt=t0
(рис.5,б), будем иметь:
![]() .
.
(40)
Спектр совокупности некоторого числа
-импульсов на
основании теоремы сложения (30) равен
![]()
![]() .
.
(41)
Периодическая последовательность
-импульсов с периодомТ
![]()
имеет линейчатый
спектр
![]() .
.
(42)
Понятие энергии для -импульса
не определено.
2.4.2.
Прямоугольный импульс
С игнал
игнал
прямоугольной формы – один из наиболее
широко используемых на практике (рис.6).
а
б
Рис. 6. Прямоугольный импульс (а) и его
спектр (б)
Спектр прямоугольного импульса
описывается формулой
![]() (43)
(43)
где
![]()
Спектр бесконечен,
имеет лепестковый характер, ширина
лепестка
![]() Энергия сигнала
Энергия сигнала![]() .
.
В центральном лепестке сосредоточено
90% всей энергии.При синтезе по
спектру для удовлетворительного
воспроизведения формы сигнала необходимо
учитывать 4 или 5 лепестков, в чем надлежит
убедиться при выполнении работы.
2.4.3.
Треугольный импульс
С игналы
игналы
треугольной формы (рис.7), как и
прямоугольной, также достаточно широко
используются на практике.
а
б
Рис.7. Треугольный импульс (а) и его
спектр (б)
Он может рассматриваться как свертка
двух прямоугольных импульсов длительностью
. Отсюда следует,
что согласно теореме о свертке (37) его
спектр равен произведению спектров
(43) этих импульсов:
![]() (44)
(44)
где
![]()
Лепестки
спектра (44) треугольного импульса имеют
ту же ширину, что у прямоугольного, но
все они положительные и затухают гораздо
быстрее. Поэтому эффективная ширина
его спектра значительно меньше чем
прямоугольного. В центральном лепестке
сосредоточено 99,7% всей энергии сигнала,
и для хорошего воспроизведения формы
треугольника при синтезе достаточно
учесть частоты только этого лепестка.
2.4.4.
Гауссов импульс
Многие явления природы, в том числе и
сигналы, описываются функцией, называемой
гауссовой (рис.8,а):
![]()

 .
.
(45)
а
б
Рис.8. Функция Гаусса (а) и ее спектр
(б)
Теоретически
протяженность функции бесконечна,
однако вследствие затухания практически
ее можно ограничить значениями от -до, где уровень
сигнала уменьшается до 4,3% от максимального.
Площадь под кривой равна 1.
Функция
эта во многих отношениях замечательная.
Так, она сама и все ее производные есть
функции абсолютно гладкие. Ее спектральнаяфункция также является гауссовой:
![]() ,
, ![]() .
.
(46)
Гауссовой
оказывается и автокорреляционнаяфункция. Замечательно и то, чтобазаэтого сигнала, выражаемая через
эффективные длительность сигнала и
полосу частот его спектра, равные![]() ,
,
имеет наименьшее из всех возможных для
сигналов значениеВ = 1:
![]()
![]() (47)
(47)
В
полосе частот от 0 до![]() заключена практически вся энергии
заключена практически вся энергии
сигнала. Этой полосы достаточно для
очень хорошего воспроизведения формы
сигнала при синтезе.
В
теоретическом плане гауссов сигнал
занимает одно из центральных мест.
Соседние файлы в папке Методички
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


Таблицы DPVA.ru – Инженерный Справочник
Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Площади неправильных фигур, объемы неправильных тел. Средняя величина сигнала. Формулы и способы расчета площади. / / Расчет средней величины сигнала.
главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Площади неправильных фигур, объемы неправильных тел. Средняя величина сигнала. Формулы и способы расчета площади. / / Расчет средней величины сигнала.
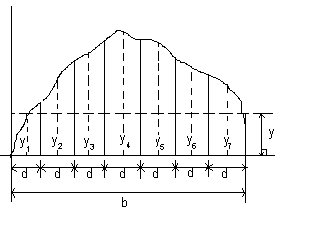
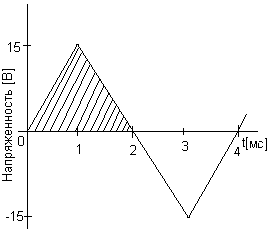
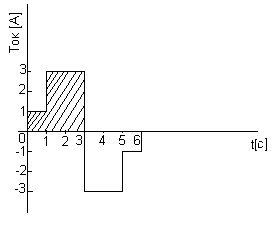
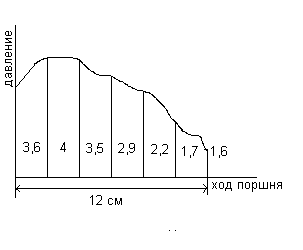
Расчет средней величины сигнала.
|
||||||||||||||||||||
|
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
![]()