Как найти площадь словосочетание

Как найти площадь фигуры

О чем эта статья:

Обозначение площади

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Если параметры фигуры переданы в разных единицах измерения длины, мы не сможем решить ни одну задачу. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Круг — это множество точек на плоскости, ограниченных окружностью, удаленных от центра на равном радиусу расстоянии. Радиусом принято называть отрезок, соединяющий центр с любой точкой окружности.

S = π × r 2 , где r — это радиус, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.

S = &pi × d 2 : 4;, где d — это диаметр.

S = L 2 ​ : (4 × π), где L — это длина окружности.

Треугольник

Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, соединенных тремя отрезками. Эти три точки принято называть вершинами, а отрезки — сторонами. Рассчитать площадь треугольника можно несколькими способами по исходными данным, давайте их рассмотрим.

1. Если известна сторона и высота.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

2. Если известны две стороны и синус угла.

S = 0,5 × a × b * sinα, где a и b — две стороны, sinα — синус угла между ними.

3. Если есть радиус описанной окружности.

S = (a × b × с) : (4 × R), где a, b и с — стороны треугольника, а R — радиус описанной окружности.

4. Если есть радиус вписанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

У нас есть отличные онлайн-занятия с лучшими преподавателями по математике для учеников с 1 по 11 классы!

Прямоугольник

Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом. Узнать площадь прямоугольника помогут следующие формулы:

S = a × b, где a, b — длина и ширина прямоугольника.

S = a × √(d 2 – а 2 ), где а — известная сторона, d — диагональ.

Диагональ — это отрезок, который соединяет несмежные вершины многоугольника. Она есть во всех фигурах, число вершин которых больше трех.

S = 0,5 × d 2 × 𝑠𝑖𝑛(𝑎), где d — диагональ, α — угол между диагоналями.

Квадрат

Квадрат — это тот же прямоугольник, но при условии, что все его стороны равны. Найти его площадь легко:

S = а 2 , где a — сторона квадрата.

S = d 2 : 2, где d — диагональ.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны и две не параллельны.

S = 0,5 × (a + b) × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны под прямым углом.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм, у которого все стороны равны.

Расскажем про общие формулы расчета площади параллелограмма и ромба.

S = a × h, где a — сторона, h — высота.

S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.

Для ромба: S = 0,5 × (d₁ × d₂), где d₁, d₂ — две диагонали. Для параллелограмма: S = 0,5 × (d₁ × d₂) × sinβ, где β — угол между диагоналями.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

0 0 0 0 0 0

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Нахождение площади фигуры, ограниченной линиями y=f(x), x=g(y)

В предыдущем разделе, посвященном разбору геометрического смысла определенного интеграла, мы получили ряд формул для вычисления площади криволинейной трапеции:

S ( G ) = ∫ a b f ( x ) d x для непрерывной и неотрицательной функции y = f ( x ) на отрезке [ a ; b ] ,

S ( G ) = – ∫ a b f ( x ) d x для непрерывной и неположительной функции y = f ( x ) на отрезке [ a ; b ] .

Эти формулы применимы для решения относительно простых задач. На деле же нам чаще придется работать с более сложными фигурами. В связи с этим, данный раздел мы посвятим разбору алгоритмов вычисления площади фигур, которые ограничены функциями в явном виде, т.е. как y = f ( x ) или x = g ( y ) .

Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)

Пусть функции y = f 1 ( x ) и y = f 2 ( x ) определены и непрерывны на отрезке [ a ; b ] , причем f 1 ( x ) ≤ f 2 ( x ) для любого значения x из [ a ; b ] . Тогда формула для вычисления площади фигуры G , ограниченной линиями x = a , x = b , y = f 1 ( x ) и y = f 2 ( x ) будет иметь вид S ( G ) = ∫ a b f 2 ( x ) – f 1 ( x ) d x .

Похожая формула будет применима для площади фигуры, ограниченной линиями y = c , y = d , x = g 1 ( y ) и x = g 2 ( y ) : S ( G ) = ∫ c d ( g 2 ( y ) – g 1 ( y ) d y .

Разберем три случая, для которых формула будет справедлива.

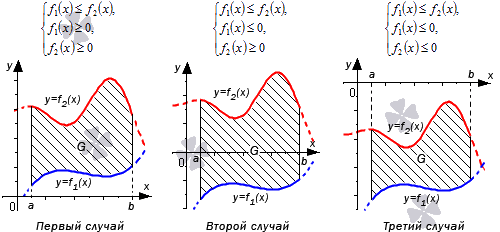
В первом случае, учитывая свойство аддитивности площади, сумма площадей исходной фигуры G и криволинейной трапеции G 1 равна площади фигуры G 2 . Это значит, что

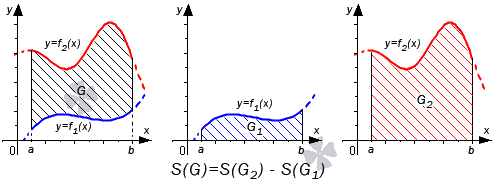
Поэтому, S ( G ) = S ( G 2 ) – S ( G 1 ) = ∫ a b f 2 ( x ) d x – ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) – f 1 ( x ) ) d x .

Выполнить последний переход мы можем с использованием третьего свойства определенного интеграла.

Во втором случае справедливо равенство: S ( G ) = S ( G 2 ) + S ( G 1 ) = ∫ a b f 2 ( x ) d x + – ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) – f 1 ( x ) ) d x

Графическая иллюстрация будет иметь вид:

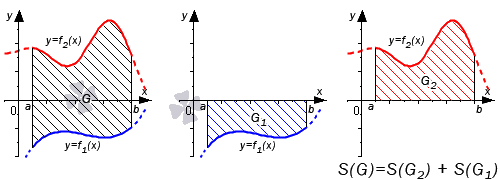
Если обе функции неположительные, получаем: S ( G ) = S ( G 2 ) – S ( G 1 ) = – ∫ a b f 2 ( x ) d x – – ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) – f 1 ( x ) ) d x . Графическая иллюстрация будет иметь вид:

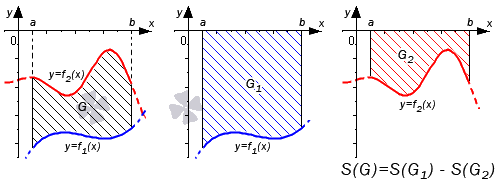
Перейдем к рассмотрению общего случая, когда y = f 1 ( x ) и y = f 2 ( x ) пересекают ось O x .

Точки пересечения мы обозначим как x i , i = 1 , 2 , . . . , n – 1 . Эти точки разбивают отрезок [ a ; b ] на n частей x i – 1 ; x i , i = 1 , 2 , . . . , n , где α = x 0 x 1 x 2 . . . x n – 1 x n = b . Фигуру G можно представить объединением фигур G i , i = 1 , 2 , . . . , n . Очевидно, что на своем интервале G i попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S ( G i ) = ∫ x i – 1 x i ( f 2 ( x ) – f 1 ( x ) ) d x , i = 1 , 2 , . . . , n

S ( G ) = ∑ i = 1 n S ( G i ) = ∑ i = 1 n ∫ x i x i f 2 ( x ) – f 1 ( x ) ) d x = = ∫ x 0 x n ( f 2 ( x ) – f ( x ) ) d x = ∫ a b f 2 ( x ) – f 1 ( x ) d x

Последний переход мы можем осуществить с использованием пятого свойства определенного интеграла.

Проиллюстрируем на графике общий случай.

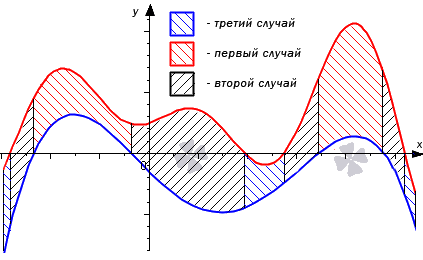
Формулу S ( G ) = ∫ a b f 2 ( x ) – f 1 ( x ) d x можно считать доказанной.

А теперь перейдем к разбору примеров вычисления площади фигур, которые ограничены линиями y = f ( x ) и x = g ( y ) .

Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)

Рассмотрение любого из примеров мы будем начинать с построения графика. Изображение позволит нам представлять сложные фигуры как объединения более простых фигур. Если построение графиков и фигур на них вызывает у вас затруднения, можете изучить раздел об основных элементарных функциях, геометрическом преобразовании графиков функций, а также построению графиков во время исследования функции.

Необходимо определить площадь фигуры, которая ограничена параболой y = – x 2 + 6 x – 5 и прямыми линиями y = – 1 3 x – 1 2 , x = 1 , x = 4 .

Решение

Изобразим линии на графике в декартовой системе координат.

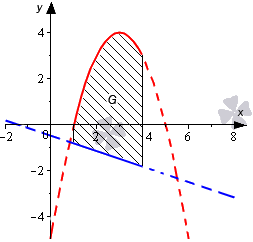
На отрезке [ 1 ; 4 ] график параболы y = – x 2 + 6 x – 5 расположен выше прямой y = – 1 3 x – 1 2 . В связи с этим, для получения ответа используем формулу, полученную ранее, а также способ вычисления определенного интеграла по формуле Ньютона-Лейбница:

S ( G ) = ∫ 1 4 – x 2 + 6 x – 5 – – 1 3 x – 1 2 d x = = ∫ 1 4 – x 2 + 19 3 x – 9 2 d x = – 1 3 x 3 + 19 6 x 2 – 9 2 x 1 4 = = – 1 3 · 4 3 + 19 6 · 4 2 – 9 2 · 4 – – 1 3 · 1 3 + 19 6 · 1 2 – 9 2 · 1 = = – 64 3 + 152 3 – 18 + 1 3 – 19 6 + 9 2 = 13

Ответ: S ( G ) = 13

Рассмотрим более сложный пример.

Необходимо вычислить площадь фигуры, которая ограничена линиями y = x + 2 , y = x , x = 7 .

Решение

В данном случае мы имеем только одну прямую линию, расположенную параллельно оси абсцисс. Это x = 7 . Это требует от нас найти второй предел интегрирования самостоятельно.

Построим график и нанесем на него линии, данные в условии задачи.

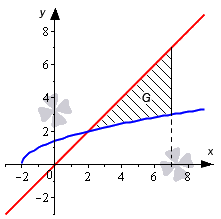
Имея график перед глазами, мы легко можем определить, что нижним пределом интегрирования будет абсцисса точки пересечения графика прямой y = x и полу параболы y = x + 2 . Для нахождения абсциссы используем равенства:

y = x + 2 О Д З : x ≥ – 2 x 2 = x + 2 2 x 2 – x – 2 = 0 D = ( – 1 ) 2 – 4 · 1 · ( – 2 ) = 9 x 1 = 1 + 9 2 = 2 ∈ О Д З x 2 = 1 – 9 2 = – 1 ∉ О Д З

Получается, что абсциссой точки пересечения является x = 2 .

Обращаем ваше внимание на тот факт, что в общем примере на чертеже линии y = x + 2 , y = x пересекаются в точке ( 2 ; 2 ) , поэтому такие подробные вычисления могут показаться излишними. Мы привели здесь такое подробное решение только потому, что в более сложных случаях решение может быть не таким очевидным. Это значит, что координаты пересечения линий лучше всегда вычислять аналитически.

На интервале [ 2 ; 7 ] график функции y = x расположен выше графика функции y = x + 2 . Применим формулу для вычисления площади:

S ( G ) = ∫ 2 7 ( x – x + 2 ) d x = x 2 2 – 2 3 · ( x + 2 ) 3 2 2 7 = = 7 2 2 – 2 3 · ( 7 + 2 ) 3 2 – 2 2 2 – 2 3 · 2 + 2 3 2 = = 49 2 – 18 – 2 + 16 3 = 59 6

Ответ: S ( G ) = 59 6

Необходимо вычислить площадь фигуры, которая ограничена графиками функций y = 1 x и y = – x 2 + 4 x – 2 .

Решение

Нанесем линии на график.

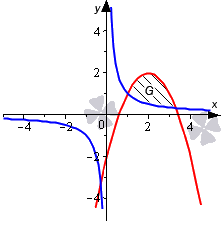
Определимся с пределами интегрирования. Для этого определим координаты точек пересечения линий, приравняв выражения 1 x и – x 2 + 4 x – 2 . При условии, что x не равно нулю, равенство 1 x = – x 2 + 4 x – 2 становится эквивалентным уравнению третьей степени – x 3 + 4 x 2 – 2 x – 1 = 0 с целыми коэффициентами. Освежить в памяти алгоритм по решению таких уравнений мы можете, обратившись к разделу «Решение кубических уравнений».

Корнем этого уравнения является х = 1 : – 1 3 + 4 · 1 2 – 2 · 1 – 1 = 0 .

Разделив выражение – x 3 + 4 x 2 – 2 x – 1 на двучлен x – 1 , получаем: – x 3 + 4 x 2 – 2 x – 1 ⇔ – ( x – 1 ) ( x 2 – 3 x – 1 ) = 0

Оставшиеся корни мы можем найти из уравнения x 2 – 3 x – 1 = 0 :

x 2 – 3 x – 1 = 0 D = ( – 3 ) 2 – 4 · 1 · ( – 1 ) = 13 x 1 = 3 + 13 2 ≈ 3 . 3 ; x 2 = 3 – 13 2 ≈ – 0 . 3

Мы нашли интервал x ∈ 1 ; 3 + 13 2 , на котором фигура G заключена выше синей и ниже красной линии. Это помогает нам определить площадь фигуры:

S ( G ) = ∫ 1 3 + 13 2 – x 2 + 4 x – 2 – 1 x d x = – x 3 3 + 2 x 2 – 2 x – ln x 1 3 + 13 2 = = – 3 + 13 2 3 3 + 2 · 3 + 13 2 2 – 2 · 3 + 13 2 – ln 3 + 13 2 – – – 1 3 3 + 2 · 1 2 – 2 · 1 – ln 1 = 7 + 13 3 – ln 3 + 13 2

Ответ: S ( G ) = 7 + 13 3 – ln 3 + 13 2

Необходимо вычислить площадь фигуры, которая ограничена кривыми y = x 3 , y = – log 2 x + 1 и осью абсцисс.

Решение

Нанесем все линии на график. Мы можем получить график функции y = – log 2 x + 1 из графика y = log 2 x , если расположим его симметрично относительно оси абсцисс и поднимем на одну единицу вверх. Уравнение оси абсцисс у = 0 .

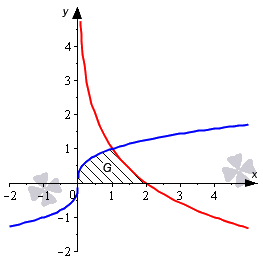
Обозначим точки пересечения линий.

Как видно из рисунка, графики функций y = x 3 и y = 0 пересекаются в точке ( 0 ; 0 ) . Так получается потому, что х = 0 является единственным действительным корнем уравнения x 3 = 0 .

x = 2 является единственным корнем уравнения – log 2 x + 1 = 0 , поэтому графики функций y = – log 2 x + 1 и y = 0 пересекаются в точке ( 2 ; 0 ) .

x = 1 является единственным корнем уравнения x 3 = – log 2 x + 1 . В связи с этим графики функций y = x 3 и y = – log 2 x + 1 пересекаются в точке ( 1 ; 1 ) . Последнее утверждение может быть неочевидным, но уравнение x 3 = – log 2 x + 1 не может иметь более одного корня, так как функция y = x 3 является строго возрастающей, а функция y = – log 2 x + 1 строго убывающей.

Дальнейшее решение предполагает несколько вариантов.

Вариант №1

Фигуру G мы можем представить как сумму двух криволинейных трапеций, расположенных выше оси абсцисс, первая из которых располагается ниже средней линии на отрезке x ∈ 0 ; 1 , а вторая ниже красной линии на отрезке x ∈ 1 ; 2 . Это значит, что площадь будет равна S ( G ) = ∫ 0 1 x 3 d x + ∫ 1 2 ( – log 2 x + 1 ) d x .

Вариант №2

Фигуру G можно представить как разность двух фигур, первая из которых расположена выше оси абсцисс и ниже синей линии на отрезке x ∈ 0 ; 2 , а вторая между красной и синей линиями на отрезке x ∈ 1 ; 2 . Это позволяет нам найти площадь следующим образом:

S ( G ) = ∫ 0 2 x 3 d x – ∫ 1 2 x 3 – ( – log 2 x + 1 ) d x

В этом случае для нахождения площади придется использовать формулу вида S ( G ) = ∫ c d ( g 2 ( y ) – g 1 ( y ) ) d y . Фактически, линии, которые ограничивают фигуру, можно представить в виде функций от аргумента y .

Разрешим уравнения y = x 3 и – log 2 x + 1 относительно x :

y = x 3 ⇒ x = y 3 y = – log 2 x + 1 ⇒ log 2 x = 1 – y ⇒ x = 2 1 – y

Получим искомую площадь:

S ( G ) = ∫ 0 1 ( 2 1 – y – y 3 ) d y = – 2 1 – y ln 2 – y 4 4 0 1 = = – 2 1 – 1 ln 2 – 1 4 4 – – 2 1 – 0 ln 2 – 0 4 4 = – 1 ln 2 – 1 4 + 2 ln 2 = 1 ln 2 – 1 4

Ответ: S ( G ) = 1 ln 2 – 1 4

Необходимо вычислить площадь фигуры, которая ограничена линиями y = x , y = 2 3 x – 3 , y = – 1 2 x + 4 .

Решение

Красной линией нанесем на график линию, заданную функцией y = x . Синим цветом нанесем линию y = – 1 2 x + 4 , черным цветом обозначим линию y = 2 3 x – 3 .

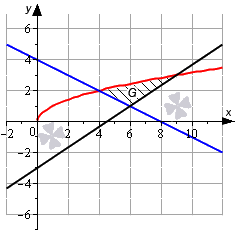
Отметим точки пересечения.

Найдем точки пересечения графиков функций y = x и y = – 1 2 x + 4 :

x = – 1 2 x + 4 О Д З : x ≥ 0 x = – 1 2 x + 4 2 ⇒ x = 1 4 x 2 – 4 x + 16 ⇔ x 2 – 20 x + 64 = 0 D = ( – 20 ) 2 – 4 · 1 · 64 = 144 x 1 = 20 + 144 2 = 16 ; x 2 = 20 – 144 2 = 4 П р о в е р к а : x 1 = 16 = 4 , – 1 2 x 1 + 4 = – 1 2 · 16 + 4 = – 4 ⇒ x 1 = 16 н е я в л я е т с я р е ш е н и е м у р а в н е н и я x 2 = 4 = 2 , – 1 2 x 2 + 4 = – 1 2 · 4 + 4 = 2 ⇒ x 2 = 4 я в л я е т с я р е ш е н и е м у р а в н и н и я ⇒ ( 4 ; 2 ) т о ч к а п е р е с е ч е н и я y = x и y = – 1 2 x + 4

Найдем точку пересечения графиков функций y = x и y = 2 3 x – 3 :

x = 2 3 x – 3 О Д З : x ≥ 0 x = 2 3 x – 3 2 ⇔ x = 4 9 x 2 – 4 x + 9 ⇔ 4 x 2 – 45 x + 81 = 0 D = ( – 45 ) 2 – 4 · 4 · 81 = 729 x 1 = 45 + 729 8 = 9 , x 2 45 – 729 8 = 9 4 П р о в е р к а : x 1 = 9 = 3 , 2 3 x 1 – 3 = 2 3 · 9 – 3 = 3 ⇒ x 1 = 9 я в л я е т с я р е ш е н и е м у р а в н е н и я ⇒ ( 9 ; 3 ) т о ч к а п е р е с е ч а н и я y = x и y = 2 3 x – 3 x 2 = 9 4 = 3 2 , 2 3 x 1 – 3 = 2 3 · 9 4 – 3 = – 3 2 ⇒ x 2 = 9 4 н е я в л я е т с я р е ш е н и е м у р а в н е н и я

Найдем точку пересечения линий y = – 1 2 x + 4 и y = 2 3 x – 3 :

– 1 2 x + 4 = 2 3 x – 3 ⇔ – 3 x + 24 = 4 x – 18 ⇔ 7 x = 42 ⇔ x = 6 – 1 2 · 6 + 4 = 2 3 · 6 – 3 = 1 ⇒ ( 6 ; 1 ) т о ч к а п е р е с е ч е н и я y = – 1 2 x + 4 и y = 2 3 x – 3

Дальше мы можем продолжить вычисления двумя способами.

Способ №1

Представим площадь искомой фигуры как сумму площадей отдельных фигур.

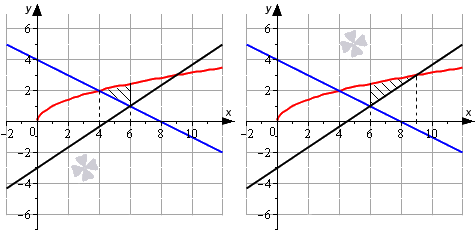
Тогда площадь фигуры равна:

S ( G ) = ∫ 4 6 x – – 1 2 x + 4 d x + ∫ 6 9 x – 2 3 x – 3 d x = = 2 3 x 3 2 + x 2 4 – 4 x 4 6 + 2 3 x 3 2 – x 2 3 + 3 x 6 9 = = 2 3 · 6 3 2 + 6 2 4 – 4 · 6 – 2 3 · 4 3 2 + 4 2 4 – 4 · 4 + + 2 3 · 9 3 2 – 9 2 3 + 3 · 9 – 2 3 · 6 3 2 – 6 2 3 + 3 · 6 = = – 25 3 + 4 6 + – 4 6 + 12 = 11 3

Способ №2

Площадь исходной фигуры можно представить как сумму двух других фигур.

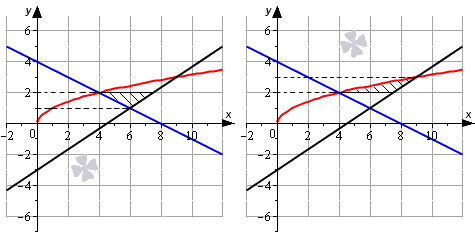
Тогда решим уравнение линии относительно x , а только после этого применим формулу вычисления площади фигуры.

y = x ⇒ x = y 2 к р а с н а я л и н и я y = 2 3 x – 3 ⇒ x = 3 2 y + 9 2 ч е р н а я л и н и я y = – 1 2 x + 4 ⇒ x = – 2 y + 8 с и н я я л и н и я

Таким образом, площадь равна:

S ( G ) = ∫ 1 2 3 2 y + 9 2 – – 2 y + 8 d y + ∫ 2 3 3 2 y + 9 2 – y 2 d y = = ∫ 1 2 7 2 y – 7 2 d y + ∫ 2 3 3 2 y + 9 2 – y 2 d y = = 7 4 y 2 – 7 4 y 1 2 + – y 3 3 + 3 y 2 4 + 9 2 y 2 3 = 7 4 · 2 2 – 7 4 · 2 – 7 4 · 1 2 – 7 4 · 1 + + – 3 3 3 + 3 · 3 2 4 + 9 2 · 3 – – 2 3 3 + 3 · 2 2 4 + 9 2 · 2 = = 7 4 + 23 12 = 11 3

Как видите, значения совпадают.

Ответ: S ( G ) = 11 3

Итоги

Для нахождения площади фигуры, которая ограничена заданными линиями нам необходимо построить линии на плоскости, найти точки их пересечения, применить формулу для нахождения площади. В данном разделе мы рассмотрели наиболее часто встречающиеся варианты задач.

Формулы площадей всех основных фигур

1. Формула площади круга через радиус или диаметр

Зная диаметр или радиус круга, можно найти его площадь.

r – радиус круга

D – диаметр

Формула площади круга, (S):

2. Формула расчета площади треугольника

h – высота треугольника

a – основание

Площадь треугольника (S):

3. Площадь треугольника, формула Герона

a , b , c , – стороны треугольника

p– полупериметр, p=( a + b + c )/2

Формула ( Герона ) площади треугольника через полупериметр ( S ):

4. Площадь прямоугольного треугольника по катетам

Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.

a , b – катеты треугольника

Формула площади прямоугольного треугольника, (S):

5. Как вычислить площадь равнобедренного треугольника ?

b – основание треугольника

a – равные стороны

h – высота

Формула площади треугольника через высоту h и основание b , ( S ):

Формула площади треугольника через, стороны a , b , (S):

6. Площадь равностороннего треугольника равна:

Формулы расчета, площади равностороннего треугольника.

a – сторона треугольника

h – высота

Площадь треугольника только через сторону a , (S):

Площадь треугольника только через высоту h , ( S ):

Площадь треугольника через сторону a и высоту h , (S):

7. Найти площадь треугольника, угол и две стороны

Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.

a , b , c – стороны треугольника

α , β , γ – углы

Формулы площади треугольника, через две стороны и угол между ними, ( S ):

8. Площадь треугольника по стороне и двум углам, формула.

a , b , c – стороны треугольника

α , β , γ – противолежащие углы

Площадь треугольника через сторону и два угла (S):

9. Формула расчета площади прямоугольника

b – длина прямоугольника

a – ширина

Формула площади прямоугольника, (S):

10. Как рассчитать площадь квадрата через диагональ или сторону

a – сторона квадрата

c – диагональ

Формула площади квадрата через сторону a , (S):

Формула площади квадрата через диагональ c , (S):

11. Формулы площади параллелограмма

1. Формула площади параллелограмма через стороны и углы

a, b – стороны параллелограмма

α , β – углы параллелограмма

Формула площади через стороны и углы параллелограмма, ( S ):

2. Формула площади параллелограмма через сторону и высоту

a, b – стороны параллелограмма

H _b – высота на сторону b

H _a – высота на сторону a

Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D – большая диагональ

d – меньшая диагональ

α , β – углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними , (S):

12. Площадь произвольной трапеции

1. Формула площади трапеции через основания и высоту

b – верхнее основание

a – нижнее основание

m – средняя линия

h – высота трапеции

Формула площади трапеции, (S):

2. Формула площади трапеции через диагонали и угол между ними

d ₁, d ₂ – диагонали трапеции

α , β – углы между диагоналями

Формула площади трапеции, (S):

3. Формула площади трапеции через четыре стороны

b – верхнее основание

a – нижнее основание

c, d – боковые стороны

Формула площади трапеции, (S):

13. Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

b – верхнее основание

a – нижнее основание

c – равные боковые стороны

α – угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R – радиус вписанной окружности

D – диаметр вписанной окружности

O – центр вписанной окружности

H – высота трапеции

α , β – углы трапеции

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d – диагональ трапеции

α , β – углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m – средняя линия трапеции

c – боковая сторона

α , β – углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b – верхнее основание

a – нижнее основание

h – высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/integraly-integrirovanie/nahozhdenie-ploschadi-figury-ogranichennoj-linijam/

http://www-formula.ru/2011-09-19-02-39-24/2011-09-24-00-19-17

[/spoiler]

Эта статья – часть проекта по математике, на котором я помогаю ученикам 8-9 классов и их родителям лучше понимать этот предмет и готовиться к ОГЭ в 9 классе.

Здравствуйте, уважаемые читатели. Сегодня мы продолжим с Вами учиться применять различные математические операции при работе с квадратными корнями, а также находить площадь треугольника общего вида и решать геометрические задачи, связанные с понятием площади треугольника. Я выдам Вам задание на дом и прикреплю в разделе “Комментарии” ответы к нему.

В предыдущей публикации “ОГЭ. Задание 8: квадратные корни. Задание 15: 2 мнения о том, что такое треугольник и его площадь” я дала понятие квадратного корня и площади треугольника. Если Вы впервые на проекте, прочитайте, пожалуйста, сначала эту статью, так как мы будем пользоваться правилами, о которых идёт в ней речь. Ссылки на все написанные статьи цикла “Решаем вместе математику, 8-9 классы” я прикреплю в конце.

Перейдём теперь к геометрии. О понятии треугольника и его площади я написала в статье, на которую дала ссылку выше. Ещё раз подчеркну, что со словосочетанием “площадь треугольника” (так же, как и со словосочетанием “площадь многоугольника”) я не согласна (так как линии нельзя поставить в соответствие число, называемое площадью). Но это – моя точка зрения.

Что такое площадь многоугольника?

В “школьной” геометрии под площадью многоугольника понимают положительную величину, которая обладает следующими свойствами:

• равные многоугольники имеют равные площади;
• если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
• за единицу измерения площади принимают единичный квадрат, т. е. квадрат со стороной, длина которой равна единице измерения длины.

В следующих статьях цикла мы рассмотрим другие формулы, с помощью которых можно вычислить площадь треугольника. А теперь решим задачи, затрагивающие понятие площади треугольника.

Задание Дана 6 для самостоятельного решения

Ответы для проверки находятся в разделе “Комментарии”.

Приятный бонус для потрудившихся:

Ссылки на предыдущие Даны.

Дан 1. “ОГЭ. Задание 6: десятичные дроби. Задание 15: углы”

Дан 2. “ОГЭ. Задание 6: обыкновенные дроби. Задание 15: треугольники общего вида”

Дан 3. “ОГЭ. Задание 6: сложные задачи-микс с десятичными и обыкновенными дробями”

Дан 4. “ОГЭ. Учимся решать геометрические задачи. Задание 15: свойства элементов треугольников общего вида”

Дан 5. “ОГЭ. Задание 8: квадратные корни. Задание 15: 2 мнения о том, что такое треугольник и его площадь”

Как Ваши успехи, уважаемые читатели? Вы можете всегда задать вопросы, если что-то не получается решить. Сложно Вам или нет решать подготовленные для Вас задания?

Вы находитесь на дружелюбном канале.

Уважайте себя. С уважением, автор.

#математика #проект по математике для 9 класса #огэ по математике #школьное образование #репетитор по математике #обучение математике

Перейти к содержимому Меню Закрыть

ГДЗ, ответы, контрольные работы, решение заданий, тесты на Знания.ком

Искать:

Знания.ком

Меню

Знания.ком

Искать:

Меню

ГДЗ, ответы, контрольные работы, решение заданий, тесты на Знания.ком

Искать:

Кнопка

Словосочетания и фразы со словом «площадь»



Придумали 94 словосочетания со словом «площадь»: подобрали слова разных частей речи (глаголы, прилагательные, причастия, существительные), составили 10 словосочетаний с предлогами и 10 словосочетаний из нескольких слов. Выпишите из таблицы составленные примеры в соответствии с вашим заданием.

Словосочетания из нескольких слов

Примеры словосочетаний из нескольких слов разных частей речи:

• площадь водного зеркала → существительное + прилагательное + существительное;
• общая площадь помещений → прилагательное + существительное + существительное;
• площадь торгового зала → существительное + прилагательное + существительное;
• большая площадь поверхности → прилагательное + существительное + существительное;
• окинуть взглядом площадь → глагол + существительное + существительное;
• площадь белорусского вокзала → существительное + прилагательное + существительное;
• привести кого-либо на площадь → глагол + местоимение-существительное + предлог + существительное;
• главная городская площадь → прилагательное + прилагательное + существительное;
• поехать на старую площадь → глагол + предлог + прилагательное + существительное;
• на небольшую площадь с фонтаном → предлог + прилагательное + существительное + предлог + существительное;

Словосочетания с предлогами

• прибежать на площадь → глагол + предлог + существительное;
• вылететь на площадь → глагол + предлог + существительное;
• спешить на площадь → глагол + предлог + существительное;
• повернуть на площадь → глагол + предлог + существительное;
• зашагать через площадь → глагол + предлог + существительное;
• идти на площадь → глагол + предлог + существительное;
• переместились на площадь → глагол + предлог + существительное;
• влететь на площадь → глагол + предлог + существительное;
• устремиться на площадь → глагол + предлог + существительное;
• выскочить на площадь → глагол + предлог + существительное;

Подберите словосочетания со словом площади, площадью.



Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Пример:

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:

S = a²

Площадь прямоугольника

Пример:

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

---

Свойство ниже может вам пригодиться при решении задач на площадь.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S
_ABC = S_ABCD : 2

S
_ABC = 20 : 2 = 10 см²

S
_ABC =
S
_ACD = 10 см²

---

Ваши комментарии

Оставить комментарий:

---