Как найти площадь смежных сторон прямоугольника

Как найти площадь смежных сторон прямоугольника

Выбирайте формулу, ориентируясь на известные величины.

1. Если известны две соседние стороны

Просто перемножьте две стороны прямоугольника.

  • S — искомая площадь прямоугольника;
  • a и b — соседние стороны.

2. Если известны любая сторона и диагональ

Найдите квадраты диагонали и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте длину известной стороны на полученное число.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).

3. Если известны любая сторона и диаметр описанной окружности

Найдите квадраты диаметра и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте известную сторону на полученное число.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • D — диаметр описанной окружности.

4. Если известны любая сторона и радиус описанной окружности

Найдите квадрат радиуса и умножьте результат на 4.

Отнимите от полученного числа квадрат известной стороны.

Найдите корень из результата и умножьте на него длину известной стороны.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • R — радиус описанной окружности.

5. Если известны любая сторона и периметр

Умножьте периметр на длину известной стороны.

Найдите квадрат известной стороны и умножьте полученное число на 2.

От первого произведения отнимите второе и разделите результат на 2.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • P — периметр прямоугольника (равен сумме всех сторон).

6. Если известны диагональ и угол между диагоналями

Найдите квадрат диагонали.

Разделите полученное число на 2.

Умножьте результат на синус угла между диагоналями.

  • S — искомая площадь прямоугольника;
  • d — любая диагональ прямоугольника;
  • α — любой угол между диагоналями прямоугольника.

7. Если известны радиус описанной окружности и угол между диагоналями

Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.

Умножьте полученное число на 2, а потом на синус угла между диагоналями.

  • S — искомая площадь прямоугольника;
  • R — радиус описанной окружности;
  • α — любой угол между диагоналями прямоугольника.

Читайте также 🎓❓📐

  • ТЕСТ:​ ​​Умеете ли вы считать в уме?
  • Как легко и быстро считать проценты в уме
  • Как найти площадь любого треугольника
  • ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
  • Как освоить устный счёт школьникам и взрослым
Источник

Площадь прямоугольника и квадрата

Площадь прямоугольника или квадрата – это часть плоскости, занимаемая данной фигурой.

Рассмотрим два прямоугольника  ABCD  и  A1B1C1D1:

как найти площадь прямоугольника, прямоугольники имеющие одинаковую площадь

Чтобы узнать сколько места они занимают, надо вычислить их площадь. Так как размеры прямоугольников даны в сантиметрах, то и за единицу измерения площади можно взять квадратный сантиметр.

Прямоугольник  ABCD  состоит из  4  строк, в каждой из которых по  6  квадратных сантиметров, значит всего в нём  6 · 4,  или  24 см2.  A1B1C1D1  состоит из  3  строк, по  8  квадратных сантиметров, значит в нём  8 · 3,  или  24 см2.  Оказалось, что несмотря на то, что прямоугольники имеют разные размеры, они занимают одинаковую площадь.

Из данного примера можно сделать вывод, что площадь прямоугольника равна произведению длин его смежных сторон. Общая формула:

S = a · b,

где  S  — площадь прямоугольника, а  a  и  b  — его смежные стороны.

Рассмотрим квадрат  ABCD:

как найти площадь квадрата

так как квадрат — прямоугольник, у которого все стороны равны, то в любом квадрате количество строк будет совпадать с количеством квадратных сантиметров, содержащихся в каждой строке. Квадрат  ABCD  состоит из  4  строк, по  4  квадратных сантиметра в каждой, значит в нём  4 · 4,  или  16 см2.

Из примера можно сделать вывод, что площадь квадрата равна длине любой его стороны во второй степени. Общая формула:

S = a2,

где  S  — площадь квадрата, а  a  — его сторона.

Чтобы узнать площадь прямоугольника, надо взять его длину и ширину (в одинаковых единицах измерения) и найти их произведение (площадь должна быть выражена в соответствующих единицах измерения).

Задача. Длина прямоугольного дома равна  12  метром, а ширина — на  5  метров меньше. Чему равна площадь дома?

Решение: Задача будет решаться в два действия:

1) 12 – 5 = 7 (метров)  — ширина дома.

2) 12 · 7 = 84 (м2)  — площадь дома.

Ответ:  84 м2.

Источник

Площадь прямоугольника онлайн

С помощю этого онлайн калькулятора можно найти площадь прямоугольника. Для нахождения площади прямоугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Площадь прямоугольника. Определение

Определение 1. Площадь прямоугольника − это величина той части плоскости, которую занимает прямоугольник.

Площадь прямоугольника. Доказательство

Теорема 1. Площадь S прямоугольника со смежными сторонами a и b равна произведению этих сторон :.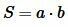

Доказательство. Рассмотрим прямоугольник со сторонами a, b и площадью S (Рис.1). Докажем, что .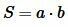

Достроим прямоугольник до квадрата со стороной a+b (Рис.2). Площадь этого квадрата равна (a+b)·(a+b) (см. статью Площадь квадрата онлайн).

С другой стороны, данный квадрат состоит из двух квадратов со сторонами со сторонами a и b и площадями a2 и b2, соответственно и из двух прямоугольников с площадями S. Поэтому сумма площадей этих двух квадратов и двух прямоугольников равна площади квадрата со стороной a+b:

Упрощая полученное равенство, получим: .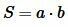

Площадь прямоугольника через стороны

Из вышеизложенной теоремы следует, что площадь прямоугольника через его смежные стороны вычисляется из формулы:

Пример 1. Стороны прямоугольника равны 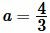и 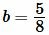. Найти площадь прямоугольника.

Решение. Для нахождения площади прямоугольника воспользуемся формулой (1). Подставим 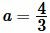, 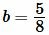в (1):

Ответ: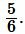

Площадь прямоугольника через сторону и диагональ

Пример 2. Известна сторона прямоугольника 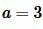и диагональ 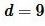(Рис.3). Найти площадь прямоугольника.

Решение. Найдем сначала неизвестную сторону прямоугольника. Для этого воспользуемся теоремой Пифагора:

Площадь прямоугольника вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления площади прямоугольника через диагональ и сторону:

Подставим 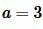, 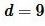в (3):

Ответ: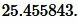

Площадь прямоугольника через периметр и сторону

Пример 3. Известны сторона прямоугольника 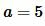и периметр 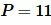(Рис.4). Найти площадь прямоугольника.

Решение. Найдем сначала неизвестную сторону прямоугольника. Для этого воспользуемся теоремой Пифагора:

Площадь прямоугольника вычисляется из формулы (1). Подставляя (4) в (1), получим формулу вычисления площади прямоугольника через периметр и сторону:

Подставим 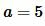, 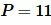в (5):

Ответ: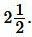

Площадь прямоугольника через диагональ и периметр

Пример 4. Известны диагональ прямоугольника 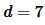и периметр 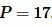(Рис.5). Найти площадь прямоугольника.

Решение. Найдем сначала стороны прямоугольника. Запишем формулу Пифагора и формулу периметра прямоугольника:

Из формулы (7) найдем ( small b ) и подставим в (6):

Упростив (9), получим квадратное уравнение относительно неизвестной ( a ):

Вычислим дискриминант квадратного уравнения (10):

Подставляя значения 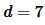и 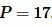в (11), получим:

Поскольку дискриминант неотрицательное число, то такой прямоугольник существует.

Стороны прямоугольника вычисляются из формул:

Почему ( small b ), как и ( small a ) получается неотрицательным, посмотрите “примечание” на странице Прямоугольник. Онлайн калькулятор.

Площадь прямоугольника по двум сторонам равна:

Подставляя (12) в (13), получим:

Далее, из (11) и (14) следует:

Подставляя 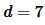, 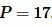в (15), получим:

Ответ: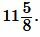

Смотрите также:

  • Прямоугольник. Онлайн калькулятор

Источник
  • Главная
  • Справочник
  • Как найти площадь прямоугольника

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость

Как найти площадь прямоугольника

Содержание:

  • Формула
  • Примеры вычисления площади прямоугольника

Формула

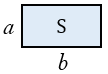
Чтобы найти площадь прямоугольника (рис. 1), надо его длину умножить на ширину, то есть

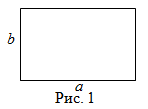
Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, то есть равны $90^{circ}$.

Примеры вычисления площади прямоугольника

Пример

Задание. Найти площадь прямоугольника, если одна его сторона равна 3 см, а вторая, смежная с ней – 5 см.

Решение. Искомая площадь прямоугольника равна произведению двух заданных сторон:

$S=3 cdot 5=15$ (см2)

Ответ. $S=15$ (см2)

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти площадь прямоугольника, если одна его сторона равна 3 м, а диагональ – 5 м.

Решение. Сделаем чертеж (рис. 2).

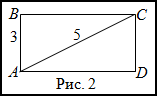
Рассмотрим прямоугольный треугольник $ABC$, из которого по
теореме Пифагора найдем длину катета $BC$ :

$B C=sqrt{A C^{2}-A B^{2}}=sqrt{5^{2}-3^{2}}=sqrt{25-9}=sqrt{16}=4$ (м)

Тогда искомая площадь равна

$S=3 cdot 4=12$ (м2)

Ответ. $S=12$ (м2)

Читать дальше: как найти площадь параллелограмма.

Статьи по теме

  • Как найти площадь
  • Как найти площадь треугольника
  • Как найти площадь ромба
  • Как найти площадь эллипса
  • Как найти площадь прямоугольного треугольника
  • Все темы раздела “Как найти площадь”

Разделы

  • Формулы сокращенного умножения
  • Формулы по физике
  • Логарифмы
  • Векторы
  • Матрицы
  • Комплексные числа
  • Пределы
  • Производные
  • Интегралы
  • СЛАУ
  • Числа
  • Дроби

Все еще сложно?

Не получается написать работу самому?

Доверь это кандидату наук!

Ищещь ответ на вопрос с которым нужна помощь?

80% ответов приходят в течение 10 минут

250 ответов по вашей теме сегодня

2 специалиста свободны онлайн

Ответы приходят уже через 10 минут

90% ответов положительные

Источник
  1. Главная
  2. Справочники
  3. Справочник по геометрии 7-9 класс
  4. Площадь
  5. Площадь прямоугольника

 Теорема

Площадь прямоугольника равна произведению его смежных сторон.

Доказательство

Дано: прямоугольник, 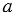, 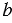– стороны, 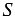– площадь.

Доказать: .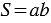

Доказательство:

Достроим прямоугольник до квадрата со стороной .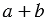

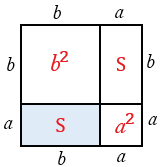
Площадь квадрата равна квадрату его стороны, значит, площадь полученного квадрата равна .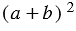

При этом полученный квадрат составлен из данного прямоугольника с площадью 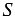, равного ему прямоугольника с площадью 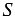(равные многоугольники имеют равные площади) и двух квадратов с площадям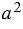и и 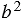(т.к. площадь квадрата равна квадрату его стороны). По свойству 20 площадей, которое говорит о том, что если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников, получаем:

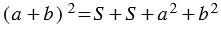или 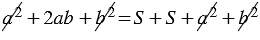, откуда .

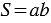Теорема доказана.

Советуем посмотреть:

Понятие площади многоугольника

Площадь квадрата

Площадь параллелограмма

Площадь треугольника

Площадь трапеции

Теорема Пифагора

Теорема, обратная теореме Пифагора

Формула Герона

Площадь


Правило встречается в следующих упражнениях:

7 класс

Задание 452,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 453,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 454,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 455,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 456,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 457,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 458,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 467,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 4,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 951,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Добавить комментарий