Формулы площадей фигур
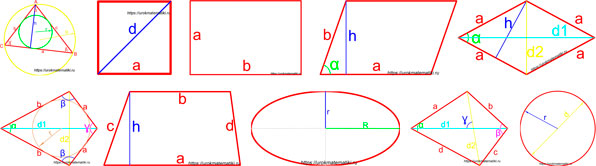
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
- формулы площади треугольника
- формулы площади квадрата
- формула площади прямоугольника
- формулы площади параллелограмма
- формулы площади ромба
- формулы площади трапеции
- формулы площади дельтоида
- формулы площади произвольного выпуклого четырехугольника
- формулы площади круга
- формула площади эллипса
Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
S = 12 a · h
,
где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.
Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c.
S = pp-ap-bp-c
,
где p — полупериметр треугольника: p = a + b + c2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 12 a · b · sinγ
,
где a, b — стороны треугольника,
γ — угол между сторонами a и b.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = a · b · c4R
,
a, b, c — стороны треугольника,
R – радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
S = p · r
,
где S — площадь треугольника,
r – радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c2
Формулы площади квадрата
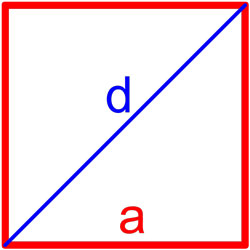
Формула площади квадрата по длине стороны

Площадь квадрата равна квадрату длины его стороны.
S = a2
,
где S — площадь квадрата,
a — длина стороны квадрата.
Формула площади квадрата по длине диагонали
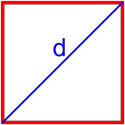
Площадь квадрата равна половине квадрата длины его диагонали.
S = d22
,
где S — площадь квадрата,
d — длина диагонали квадрата.
Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон.
S = a · b
,
где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.
Формулы площади параллелограмма
Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.
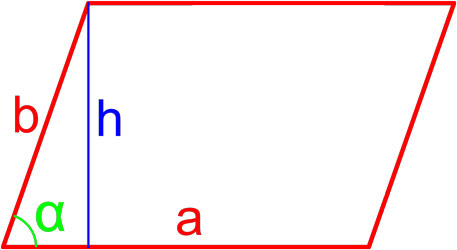
Формула площади параллелограмма по длине стороны и высоте

Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S = a · h
,
где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.
Формула площади параллелограмма по двум сторонам и углу между ними

Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
S = a · b · sinα
,
где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α – угол между сторонами параллелограмма.
Формула площади параллелограмма по двум диагоналям и углу между ними
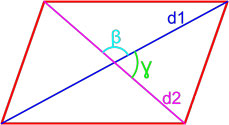
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S =
d1 · d2
· sinβ2 = d1 · d2
· sinγ2
,
где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β, γ – угол между диагоналями параллелограмма.
Формулы площади ромба
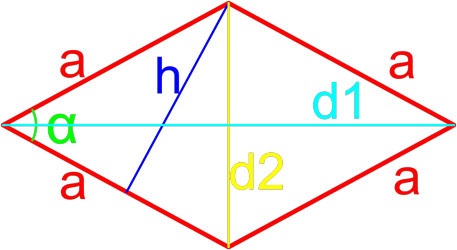
Формула площади ромба по длине стороны и высоте
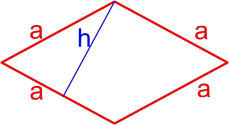
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S = a · h
,
где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.
Формула площади ромба по длине стороны и углу
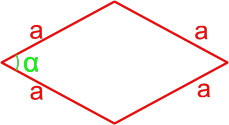
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
S = a2 · sinα
,
где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.
Формула площади ромба по длинам его диагоналей
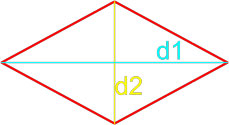
Площадь ромба равна половине произведению длин его диагоналей.
S = d1 · d22
,
где S — площадь ромба,
d1, d2 — длины диагоналей ромба.
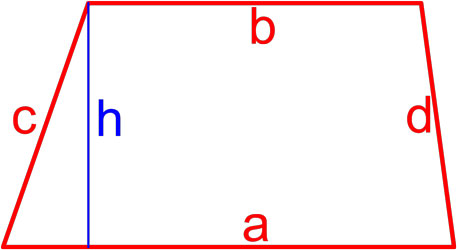
Формулы площади трапеции
Трапеция — это четырёхугольник, у которого две (a, b) стороны параллельны (основания), а две другие (c, d) стороны не параллельны (боковые стороны).
Формула Герона для трапеции
S = a + b|a – b| p-ap-bp-a-cp-a-d
,
где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p=a+b+c+d2 — полупериметр трапеции.
Формула площади трапеции по длине основ и высоте
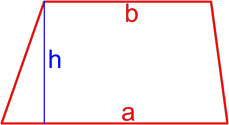
Площадь трапеции равна произведению полусуммы её оснований на высоту.
S = a + b · h2
,
где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.
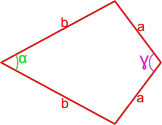
Формулы площади дельтоида
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.
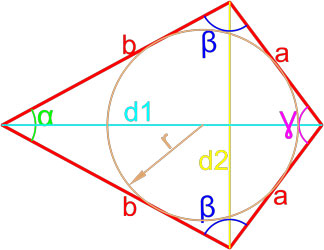
Формула площади дельтоида по двум неравным сторонам и углу между ними
Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.
S = a·b sinβ
,
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.
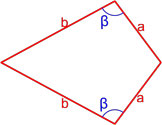
Формула площади дельтоида по равным сторонам и углу между ними
Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.
S = a2 sinγ + b2 sinα2
,
где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b,
γ — угол между равными сторонами a.
Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
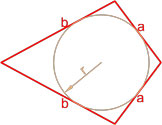
Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.
S = a+b r
,
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.
Формула площади дельтоида по двум диагоналям
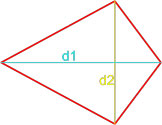
Площадь дельтоида равна половине произведения длин двух диагоналей.
S = d1 · d22
,
где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.
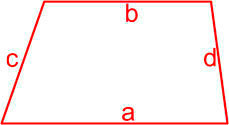
Формулы площади произвольного выпуклого четырехугольника
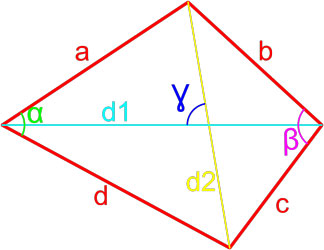
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
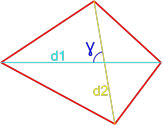
Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.
S = d1 · d2 · sinγ2
,
где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.
Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
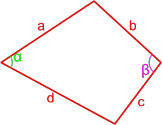
S = p-ap-bp-cp-d – a·b·c·d ·cos2θ
,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p=a+b+c+d2 — полупериметр четырехугольника,
θ = α + β2 — полусумма двух противоположных углов четырехугольника.
Формула площади вписанного четырехугольника (формула Брахмагупты)
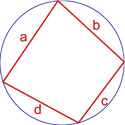
Если вокруг четырехугольника можно описать окружность, то его площадь равна
S = p-ap-bp-cp-d
,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p=a+b+c+d2 — полупериметр четырехугольника.
Формула площади четырехугольника с вписанной окружностью
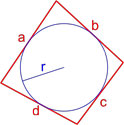
Если в четырехугольник можно вписать окружность, то его площадь равна:
S = p· r
,
где S — площадь четырехугольника,
r — радиус вписанной окружности,
p=a+b+c+d2 — полупериметр четырехугольника.
Формула площади четырехугольника с вписанной и описанной окружностями
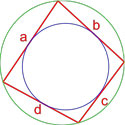
Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:
S = a·b·c·d
,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.
Формулы площади круга
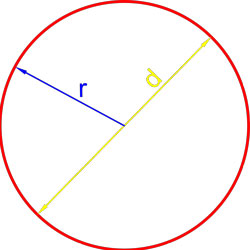
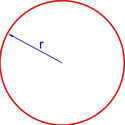
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
S = πr2
,
где S — площадь круга,
r — радиус круга.
Формула площади круга через диаметр
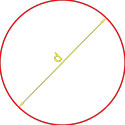
Площадь круга равна четверти произведения квадрата диаметра на число пи.
S = πd24
,
где S — площадь круга,
d — диаметр круга.
Площадь сегмента круга
Площадь кругового сегмента через угол в градусах.
S = R22 · π · α°180° – sinα
,
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.
Площадь кругового сегмента через угол в радианах.
S = R22 · αрад. – sinα
,
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.
Формула площади эллипса
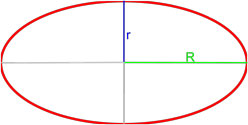
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S = π · a · b
,
где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
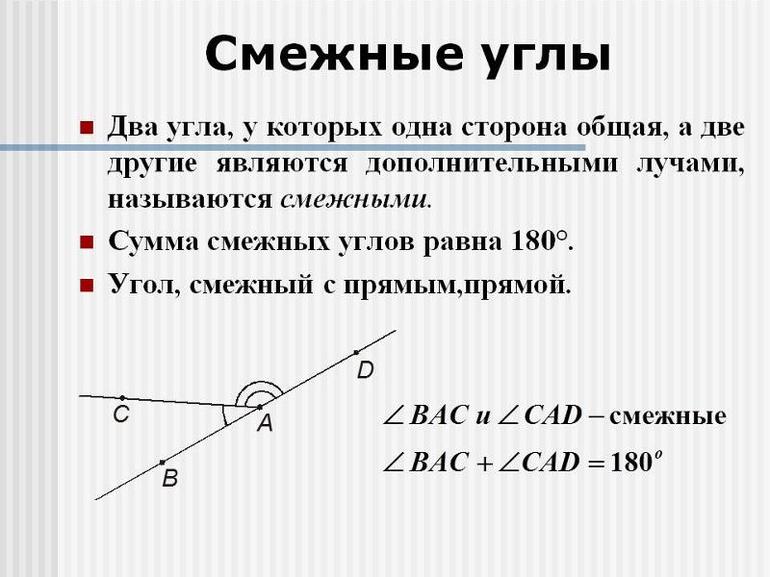
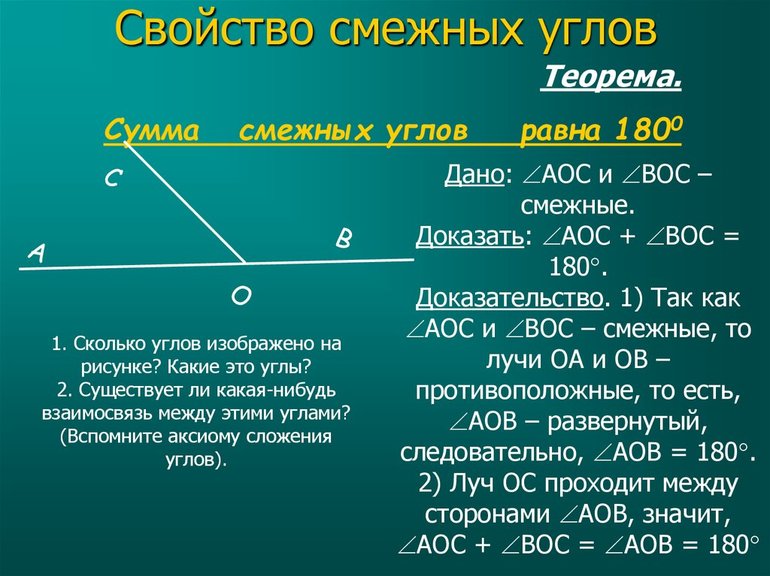
Что такое смежные углы? Какие у них свойства?
Определение.
Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой.

∠1 и ∠2 — смежные углы
Сколько смежных углов образуется при пересечении двух прямых?
При пересечении двух прямых образуется четыре пары смежных углов:

∠1 и ∠2, ∠3 и ∠4,
∠1 и ∠3, ∠2 и ∠4
Но, так как ∠1 =∠4, ∠2=∠3 (как вертикальные), то достаточно рассмотреть только одну из этих пар.
Свойство смежных углов.
Сумма смежных углов равна 180º.
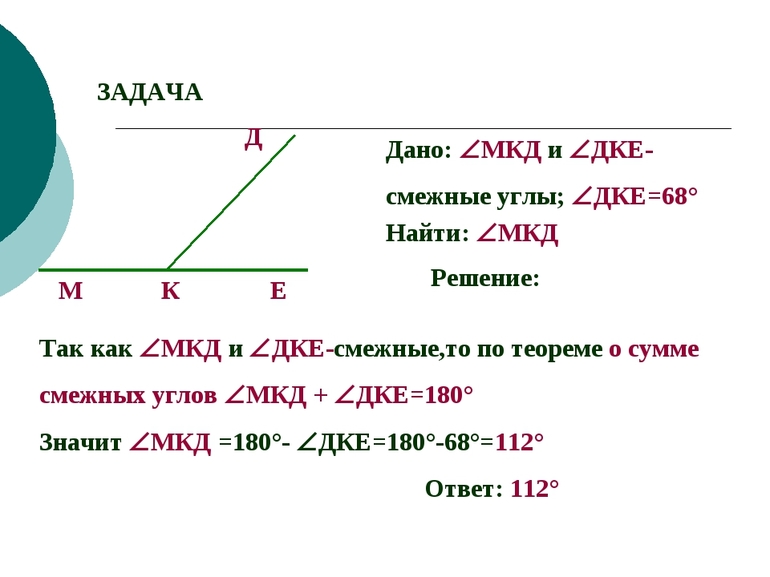
Задачи.
1) Даны два смежных угла. Один на 42 градуса больше другого. Найти эти углы.

Дано:
∠AOC и ∠BOC — смежные,
∠AOC на 42º больше, чем ∠BOC
Найти: ∠AOC и ∠BOC.
Решение:
Пусть ∠BOC=хº, тогда ∠AOC= х+42º. Так как сумма смежных углов равна 180º, то ∠BOC+∠AOC=180º.
Имеем уравнение:
х+х+42=180
2х=180-42
2x=138
x=69
Значит, ∠BOC= 69º, ∠AOC=69+42=111º.
Ответ: 69º и 111º.
2) Найти смежные углы, если их градусные меры относятся как 4:5.

Дано:
∠1 и ∠2 — смежные,
∠1 : ∠2= 4:5
Найти:∠1 и ∠2
Решение:
Пусть k — коэффициент пропорциональности. Тогда ∠2 =4kº , ∠1=5kº. Так как сумма смежных углов равна 180º, ∠1 +∠2=180º.
Имеем уравнение:
4k+5k=180
9k=180
k=20
Значит, смежные углы равны 4∙20=80º и 5∙20=100º.
Ответ: 80º и 100º.
3) Один из углов, образованных при пересечении двух прямых, в 5 раз больше другого. Найти эти углы.

Дано: AB и CD — прямые, O — точка их пересечения,
∠AOD в 5 раз больше, чем ∠BOD
Найти: ∠AOD, ∠BOD
Решение:
При пересечении двух прямых образуются смежные и вертикальные углы. Так как вертикальные углы равны между собой, то углы∠AOD и ∠BOD — смежные. Пусть ∠BOD=xº, тогда ∠AOD=5xº. Так как сумма смежных углов равна 180º, ∠AOD +∠BOD=180º.
Имеем уравнение:
x+5x=180
6x=180
x=30
Значит, ∠BOD=30º, ∠AOD=5∙30=150º.
Ответ: 30º и 150º.
Могут ли смежные углы быть равными?
Да. Если смежные углы равны между собой, то, так как сумма смежных углов равна 180º, каждый из них равен половине суммы, то есть 90º.
Вывод:
угол, смежный с прямым, есть прямой угол.
Могут ли два смежных угла быть тупыми? Острыми?
Нет. Так как градусная мера тупого угла больше 90º, то сумма двух тупых углов больше 180º. А сумма смежных углов равна 180º.
Градусная мера острого угла меньше 90º. Значит, сумма двух острых углов меньше 180º.
Таким образом, в паре смежных углов один — тупой, другой — острый (или оба прямые).

Общие сведения
Основными элементами, используемыми в геометрии, являются лучи и углы. С их помощью образуется любая геометрическая фигура — квадрат, треугольник или любого вида многоугольник. Луч — это полупрямая, то есть часть линии, на которой точки располагаются по одной стороне от зафиксированной. По-другому можно сказать, что луч — это линия, ограниченная только с одной стороны. Обозначают его как прописными латинскими буквами, так и заглавными с названием точек. Во втором случае первой указывается начальная точка.
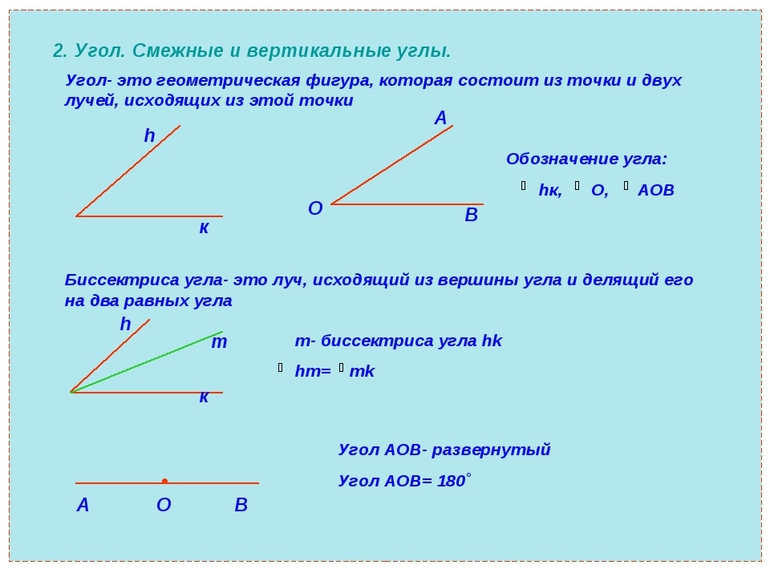
Два луча, выходящие из одной точки, образовывают угол. По сути, это незамкнутая геометрическая фигура. Она имеет вершину (общую точку) и стороны. Обозначают его с помощью трёх заглавных букв, соответствующих трём точкам — вершине и двум лежащим на разных сторонах лучах. Внутренняя часть формируется из множества точек, принадлежащих плоскости, ограниченной сторонами угла.
Существует шесть видов углов:
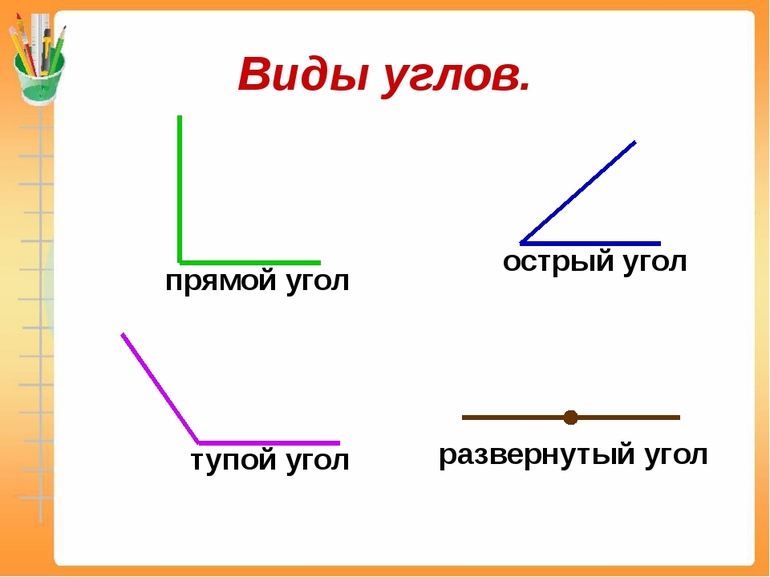
- Острый — расстояние между сторонами составляет меньше 90 градусов.
- Прямой — образовывается двумя взаимно перпендикулярными прямыми.
- Тупой — разворот угла больше 90 градусов, но не превышает 180.
- Развёрнутый — представляет сумму двух прямых элементов.
- Выпуклый — угол между лучами составляет больше 180 градусов, но меньше 360.
- Полный — равняется 360 градусам.
Располагаясь на плоскости, по отношению друг к другу углы могут быть смежными или вертикальными. Согласно определению, смежными углами называют такую пару, у которой одна сторона принадлежит обеим фигурам, а два других луча образуют прямую линию. Вертикальными же считаются углы, стороны которых дополняют друг друга до прямых линий. Они всегда градусно равны.
Из угла всегда можно провести линию, делящую его на две равные части. Такой луч, исходящий из вершины, называют биссектрисой. А это значит, что после его проведения образуется два равных смежных угла, обладающих одинаковыми свойствами.
Единицей измерения разворота фигуры является градусная мера. Если в нём содержится нецелое количество градусов, то используются минуты и секунды. Так, в одном градусе содержится 60 минут, а в одной минуте 60 секунд.
Основные факты
Вычисление элементов треугольников используется в географии, строительстве, астрономии, мореплавании и других науках и технике, например, кинематике, механике, оптике, при проведении гармонического анализа. Для успешного решения задач по теме нужно знать следующие факты:
- При пересечении двух лучей образуются стороны, которые являются продолжением друг друга, при этом образованные угловые элементы будут вертикальными.
- Сумма угловых частей в треугольнике при сложении составляет 180 градусов.
- Биссектрисы смежных частей взаимно перпендикулярны.
- Если существуют односторонние угловые элементы, то при параллельных линиях они будут перпендикулярными.
- Если точка располагается на равноудалённом расстоянии от угловой стороны, то она находится на биссектрисе.
- Равнобедренным называют треугольник с двумя равными сторонами, при этом высота и медиана у него совпадают. Отсюда следует, что два угла в такой фигуре равны.
- Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилегающим сторонам.
- Точка пересечения медиан в треугольнике делит их в отношении один к двум, начиная отсчёт от вершины.
- Медиана, построенная из вершины прямого угла, равняется одной второй гипотенузы.
- Высота в треугольнике делит его на две фигуры, подобные начальной.
- Средняя линия треугольника представляет вектор, состоящий из середин двух его сторон, при этом она параллельна третьей стороне и отсекает от фигуры подобный треугольник.
- Катет, примыкающий к вершине угловой части объекта, называется прилежащим и формирует его совместно с гипотенузой. Другой же луч, не примыкающий к элементу, находится напротив вершины и является противолежащим.
- Синусом называется отношение противолежащего катета к гипотенузе, а косинусом — отношение прилежащего к угловому элементу катету к гипотенузе.
Кроме этого, нужно учесть, что отличие смежных углов от вертикальных заключается в том, что сумма первых равняется 180 градусам, а вторые всегда равняются друг другу.
Иными словами, для пары углов смежным будет угловой элемент, равный у = (180 — x) градусам. Причём при пересечении двух лучей получается четыре смежные пары, из которых две будут вертикальными. Это основополагающие факты, на которых построена геометрия и тригонометрия. Зная их, можно переходить к изучению таких сложных наук, как, например, планиметрия и стереометрия.
Свойства и теорема
С теоремой о смежных углах знакомят на уроках геометрии в седьмом классе средней школы. Исходя из того, что такие фигуры имеют общую вершину и сторону, можно предположить, что сумма углов будет равняться 180 градусам. При этом каждый из них способен дополнить другой до развёрнутого. Равенство суммы 180 градусам и является основной теоремой.
Доказательство этого утверждения выполняется довольно просто. Делается это путём изображения пары смежных углов ABC и CBK. Вершина располагается в точке B, а сторона BC является общей. Изучив рисунок, можно отметить, что стороны AB и BK лежат на одной прямой. По аксиоме измерения углов получается, что ∠ABC + ∠СBK = ∠ABK. Иными словами, полученные углы образовывают развёрнутый, то есть такой, значение которого равняется 180 градусам. Формулой теорему можно записать как ∠ABC + ∠CBK = 1800.
На основании рассмотренной теоремы вытекают три свойства смежных углов:
- если они равны, то они являются прямыми;
- угол, смежный с тупым, — острый, и наоборот;
- когда два угла равны, то будут равными и смежные с ними развороты.

А также существуют следствия или, как их ещё называют, тригонометрические соотношения. В их основе лежит то, что косинусы и тангенсы рассматриваемых фигур всегда будут равны по величине, но противоположны по знаку. При этом если необходимо построить угол, смежный с существующим, то нужно одну из сторон продлить за вершину.
Указанные свойства используются и при определении подобия треугольников. Например, согласно первому признаку, если два угла равностороннего или разностороннего треугольника совпадают с двумя углами другого, то они подобны. Случается, что по одну сторону от линии могут находиться несколько лучей, имеющих общую вершину. Изобразив такую ситуацию на чертеже, легко убедиться, что если все полученные углы сложить, то их сумма будет соответствовать значению двух прямых, а также из них всегда можно образовать смежную пару.
Этот свойство используется тогда, когда необходимо определить, чему равняется сумма углов вокруг конкретно взятой вершины. То есть продолжив одну из сторон за рассматриваемую вершину, можно получить две группы: первую — сумма которых равна двум прямым, и вторую — сумма которых также равна двум прямым углам. Отсюда следует, что сумма вокруг общей вершины будет равняться прямым углам.
Примеры решения задач
Решать задачи по заданной теме проще, если выполнять чертежи. С их помощью, а также зная свойства и теоремы, найти правильный ответ не составит особого труда. Существуют типовые задания, позволяющие закрепить пройденный материал и на практике применить полученные знания. Вот наиболее интересные из них с подобным решением:

- Возможно ли существование такой смежной пары, в которой будут два остроугольника? Для ответа на вопрос нужно рассуждать следующим образом. Острым называется такой элемент, разворот которого меньше 90 градусов. Так как пара должна содержать общую сторону, то второй элемент будет тупоугольным. Исключением будет, если из вершины лучи выходят перпендикулярно друг другу, поэтому существование такой пары невозможно.
- Один из парных элементов меньше другого на 80 градусов, необходимо найти разворот второго. Итак, если первый угол принять равным U, то второй, согласно условию, будет равняться U — 80. Так как в сумме они оба дают 180 градусов, то верным будут следующие уравнения: U + U + 66 = 180; 2 * U = 180 — 80; 2 * U = 100; U = 100/2 = 50. Отсюда разворот второго элемента составит: 50 + 80 = 130 градусов.
- Имеются два прямоугольных треугольника со смежными между собой углами, при этом их меры в градусах относятся как 2:3. Чтобы найти их значения, нужно вспомнить, что сумма смежных углов равна 180 градусам. Обозначив первый разворот два икс, а второй с коэффициентом три, справедливо будет записать: 2x + 3x = 180. Решив уравнение, можно определить икс, его значение будет равняться: x = 30. Затем, подставив вместо икса его численную величину, довольно просто вычислить ответ. Искомые значения будут 60 и 90 градусов.
- Восьмая часть одного из смежных элементов и три четверти другого составляют в сумме прямую фигуру. Нужно найти разность. Так как сумма парных углов 180°, то пусть один из них равняется икс, тогда другой будет игрек. На основании этих данных можно составить систему: x + y = 180; x / 8+ (3у) / 4 = 90. Сложив оба уравнения, можно получить равенство: x + 6y = 720; 5y = 540. Отсюда: y = 108°, x = 180 — 108 = 72 градуса. В итоге искомая разность составит: 108 — 72 = 36.
Уметь правильно решать задачи важно, так как в дальнейшем эти знания помогают находить такие важные элементы, как площадь треугольника, зная только разворот и высоту произвольной фигуры, а далее уже легко будет вычислить и объём. Кроме этого, правила смежности часто используются в тригонометрии при нахождении синусов и косинусов.
Вычисление на онлайн-калькуляторе
Нахождение градусной меры смежных элементов обычно не вызывает проблем и относится к элементарным действиям при исследованиях различных треугольников, например, остроугольных или равнобедренных. Но при работе с нецелыми числами или в процессе обучения имеет смысл использовать так называемые онлайн-калькуляторы.
Это обычные интернет-сайты, содержащие встроенную программу для автоматических расчётов. Пользоваться ими сможет каждый, кто имеет компьютер или гаджет с установленным веб-обозревателем. Вся работа с сервисом сводится к загрузке его интернет-страницы и заполнения специальной формы, в которую вводятся исходные данные. Затем нажимается интерактивная кнопка и на дисплее появляется ответ.

Вычисление обычно занимает пару секунд, а появление ошибки исключено. Кроме этого, на сайтах, предлагающего такого рода услуги, содержится весь необходимый для расчётов теоретический материал. Поэтому даже слабо подготовленный по теме пользователь сможет понять, откуда и каким образом получился тот или иной ответ.
Из множества сервисов, существующих в русскоязычном сегменте всемирной сети, можно выделить следующие:
- fxyz;
- calc;
- geleot;
- 01math;
- infofaq.
Эти сервисы доступны бесплатно, имеют интуитивно понятный интерфейс на русском языке.
При этом пользователям предлагается ознакомиться с развёрнутым решением, то есть указан поэтапный расчёт. Для удобства на страницах даётся не только необходимая теория, но и ряд типовых примеров с подробным описанием действий.
Следует отметить, что указанные сервисы могут находить ответ для любой сложности математической задачи. Особенно востребованными становятся такие вычисления в инженерии, связанные с тригонометрическими функциями. Ведь для таких расчётов важны точность и время, что вполне могут обеспечить онлайн-калькуляторы.
Содержание:
- Формулы
- Примеры вычисления площади параллелограмма
Формулы
Первый способ. Чтобы найти площадь параллелограмма (рис. 1), нужно найти произведение стороны
$a$ параллелограмма на высоту
$h_a$, проведенную к этой стороне, то есть

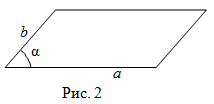
Второй способ. Чтобы найти площадь параллелограмма, надо найти произведение двух его смежных сторон
$a$ и $b$, умноженное на синус угла
$alpha$ между ними (рис. 2):
$$mathrm{S}=a b sin alpha$$
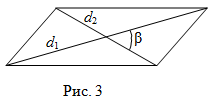
Третий способ. Чтобы найти площадь параллелограмма, надо найти полупроизведение его диагоналей
$d_1$ и $d_2$ на синус угла $beta$ между ними (рис. 3):
$$mathrm{S}=frac{1}{2} d_{1} d_{2} sin beta$$
Примеры вычисления площади параллелограмма
Пример
Задание. Найти площадь параллелограмма, если его сторона равна 2 см, а высота, проведенная к этой стороне – 3 см.
Решение. Искомая площадь равна
$S=2 cdot 3 = 6$ (см2)
Ответ. $S=6$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти площадь параллелограмма, одна сторона которого равна 4 см, вторая на 3 см
больше и тупой угол параллелограмма равен $120^{circ}$.
Решение. Найдем вторую сторону параллелограмма:
$b=4+3=7$ (см)
Так как сумма углов параллелограмма, прилежащих к одной стороне, равна
$180^{circ}$, то делаем вывод, что угол между сторонами равен
$$alpha=180^{circ}-120^{circ}=60^{circ}$$
Тогда искомая площадь равна
$mathrm{S}=4 cdot 7 cdot sin 60^{circ}=28 cdot frac{sqrt{3}}{2}=14 sqrt{3}$ (см2)
Ответ. $mathrm{S}=14 sqrt{3}$ (см2)
Остались вопросы?
Здесь вы найдете ответы.
Каким образом можно доказать утверждение о том, что площадь параллелограмма
есть число, получаемое в результате умножения длин двух его сторон,
являющихся смежными, и синуса угла, который образуется между ними?
Параллелограмм следует расположить по горизонтали. Обозначим его верхнее
основание как АВ, а противоположное ему основание – как CD. Из точек ВЕ и
AF проведем перпендикулярные прямые на нижнее основание фигуры. В
результате получится прямоугольник ABEF. Площадь образовавшейся
прямоугольной фигуры равна площади параллелограмма по той причине, что
параллелограмм ABCD и фигура с прямыми углами ABEF являются
равносоставленными, о чем свидетельствует равенство треугольников ВEC и
DAF.
Площадь (S) прямоугольника представляет собой произведение длин сторон EF
и FA, которое, в свою очередь, равно:
CD*AD*sin(CDA)
Именно это и требовалось доказать.
Параллелограмм имеет смежные стороны длиной 26 см и 32 см. Один из углов
данной фигуры равен 150 градусам. Каким способом можно вычислить площадь
параллелограмма?
Обозначим имеющийся параллелограмм как АВСD. Тогда одна его сторона АВ
равна 26 см, а другая АD – 32 см. Угол АВС параллелограмма составляет 150
градусов.
Принимая во внимание тот факт, что сумма внутренних односторонних углов
параллелограмма равна 180 градусов, можно говорить о том, что его угол ВАD
составляет 30 градусов. Проведем высоту ВК, и в итоге получим треугольник
АВК с прямым углом. Длина опущенной высоты как катета, расположенного
противоположно углу в 30 градусов, равна 13 см. Площадь (S)
параллелограмма есть число, полученное в результате умножения длины высоты
на длину стороны. Это значит, что:
S (АВСD) = 13 *32 = 416 см кв.
Ответ: Площадь параллелограмма равна 416 см кв.
Прямая АС проведена через середины двух сторон параллелограмма, которые
являются смежными. Данная прямая отсекает от параллелограмма два
треугольника – FMD и АDС. Площадь одного из отсеченных треугольников
составляет 32 см кв. Как высчитать площадь параллелограмма?
Прямая АС представляет собой диагональ биссектрисы. В этом случае
образовавшиеся посредством ее проведения треугольники FMD и АDС являются
подобными по причине наличия общего угла А и равенства сторон. На
основании этого можно говорить о том, что:
SADC=1/2*ab*sin a
SFDM=1/2 *2a*2b sin a
SADC / SFDM= 32/x
1/4=32/x
x=128
Теперь можно рассчитать площадь параллелограмма (S), которая будет равна
2*х:
S = 128*2 = 256 см кв.
Ответ: Площадь параллелограмма равна 256 см кв.
Параллелограмм имеет стороны, длины которых составляют 10 см и 6 см. Данные
стороны образуют угол, равный 150 градусам. Как рассчитать площадь
параллелограмма в этом случае?
Обозначим угол в 150 градусов буквой В. Зная о том, что внутренние
односторонние углы параллелограмма в сумме дают 180 градусов, можно
вычислить второй угол А. Он будет равен:
∠А = 180-150 = 30 градусов.
Теперь следует провести высоту ВВ1, которая образует треугольник АВВ1,
являющийся прямоугольным. Длина ВВ1 будет равна половине длины стороны,
равной 6 см:
ВВ1 = 6/2 = 3 см.
Тогда площадь (S) параллелограмма можно рассчитать, умножив длину ВВ1 на
10 см (длина смежной стороны):
S = 3*10 = 30 см кв.
Ответ: Площадь параллелограмма равна 30 см кв.
Проведенные диагонали делят параллелограмм на четыре треугольных фигуры.
Площадь одной из них равна 7 м кв. Каким образом можно найти площадь
параллелограмма?
Обозначим имеющийся параллелограмм как ABCD. Точкой пересечения его
диагоналей является точка О. Образованные диагоналями треугольные фигуры
ABO, BCO, CDO, DAO являются одинаковыми по площади. Об этом
свидетельствует тот факт, что диагонали параллелограмма делятся ровно
пополам в точке их пересечения. Свидетельством того, что все четыре
треугольника имеют одинаковые площади, выступает равенство синусов смежных
углов. Площадь является ½ числа, которое получено в результате умножения
длин сторон треугольника и синуса угла, образованного между ними.
Параметры, которые отвечают вычислению площадей треугольников, равны, а
это означает равенство и самих площадей.
Если площади всех четырех треугольных фигур равны, то площадь самого
параллелограмма будет в четыре раза превышать площадь любого из них. Это
значит, что площадь (S) параллелограмма может быть вычислена следующим
образом:
S = 4*7 = 28 м кв.
Ответ: Площадь параллелограмма равна 28 м кв.
Дан параллелограмм ABCD, на одной из сторон которого АВ поставлена точка М.
Известно, что площадь треугольника MCD составляет 38 см кв. Как найти
площадь параллелограмма?
Площадь (S) параллелограмма рассчитывается путем умножения длины его
основания на длину его высоты.
Прямые МС и МD, проведенные из точки М, делят параллелограмм на
треугольники. Площадь первого из них вычисляется как:
S₁ = 1/2 * a * h = 38 см кв.
Формула для расчета площади второго треугольника выглядит так:
S₂ = 1/2 * a₁* h
Площадь третьего треугольника можно найти следующим образом:
S₃ = 1/2 *a₃* h,
где а =а₁ + а₂
Теперь через площади образованных треугольников можно вычислить площадь
параллелограмма:
S = S₁ + S₂ + S₃ = 1/2 *(a * h +a₁ * h +a₂ * h) = 1/2 * (a * h + h(a₁ +
a₂)) = 1/2 * (a * h + a * h) = 2 * 38 = 76 см. кв.
Ответ: Площадь параллелограмма равна 76 см кв.
Длина основания параллелограмма составляет 5 см, а его высота равна 3 см.
Как найти площадь параллелограмма?
Формула расчета площади параллелограмма (S) включает длину его высоты и
длину его основания. Данные элементы нужно перемножить, для того чтобы
вычислить площадь фигуры:
S = a*h= 5*6=30 см кв.
Ответ: Параллелограмм имеет площадь 30 см кв.
Имеется параллелограмм ABCD. Посередине его стороны АВ поставлена точка Е,
из которой проведена прямая, образующая треугольник CDE площадью 36 см кв.
Каким образом можно найти площадь параллелограмма?
На продолжение стороны CD опустим перпендикуляр ЕН из точки Е. Он
представляет собой высоту для параллелограмма ABCD и треугольника CDE.
Известно, что площадь (S) параллелограмма является произведением длины его
стороны и высоты, которая на нее опущена. Площадь треугольника
представляет собой ½ от числа, которое получилось в результате умножения
длины стороны на высоту, опущенную на нее. На основании этого можно
сделать вывод о том, что:
S(ABCD) = EH*CD
S(∆CDE) = ½*EH*CD => 2*S(∆CDE) = EH*CD.
Из этого следует, что:
2*S(∆CDE) = S(ABCD) = 2*36 ед² = 72 ед. кв.
Ответ: Площадь параллелограмма составляет 72 кв. ед.
В каком виде представлена формула, которая предназначена для вычисления
площади параллелограмма?
Для получения возможности рассчитать, чему равна площадь (S)
параллелограмма, нужно располагать сведениями о длине его основания (а) и
высоты (h). В этом случае площадь можно высчитать при помощи следующей
формулы:
S = а* h.
Как найти площадь параллелограмма через синус, если известно, что длины его
сторон равны 8 см и 10 см, а синус одного из его углов составляет 0,05?
Формула, которая предназначена для вычисления площади параллелограмма (S)
через синус, выглядит следующим образом:
S = a × b × sin A
В данной формуле буквами a и b обозначены стороны параллелограмма,
являющиеся смежными, а А означает угол, который образован между этими
сторонами.
Доказано, что синусы смежных углов являются равными. Это значит, что синус
тупого угла равен синусу острого угла.
Площадь параллелограмма вычисляем следующим образом:
S = 8 × 10 × 0,05 = 4 см кв.
Ответ: Параллелограмм имеет площадь, равную 4 см кв.
Имеется параллелограмм ABCD, в котором опущена высота на его сторону АВ. Ее
длина равна 12 см. При этом длина AD составляет 24 см. Каким образом можно
высчитать значение синуса угла А?
Высота, опущенная на сторону АВ параллелограмма, обозначена как СК.
Полученный в результате треугольник КВС имеет прямой угол.
Sin B=АВ/ВС.
В этом случае ВС=AD=24 см. Так, синус угла В равен:
sinВ=12/24=1/2, что соответствует углу 30 градусов.
В параллелограмме проведены диагонали, длины которых равны 5 см и 28 см.
Между ними образован угол, составляющий 30 градусов. Как можно найти площадь
параллелограмма через синус в данном случае?
Площадь любой из четырехугольных фигур может быть вычислена, если известны
длины ее диагоналей и синус угла, образованного между ними. Для этого
нужно произвести умножение упомянутых величин, а затем разделить
полученное число на 2. В случае с параллелограммом, обозначенным как ABCD,
площадь рассчитывается по этой же формуле:
S = 1/2 AC*BD*sin∠AOB = ½*28*5*sin30° = 14*5*1/2 = 7*5 = 35 кв. см.
Ответ: Площадь параллелограмма равна 35 см кв.
Представляется ли возможным высчитать площадь параллелограмма при условии,
что длины двух его диагоналей и образованный в месте их пересечения угол
являются известными величинами?
Площадь параллелограмма (S) представляет собой половину числа, полученного
после умножения друг на друга длин проведенных в нем диагоналей, которое
умножено на синус образовавшегося в итоге их пересечения угла:
S = ½*d 1*d 2*sin α
Возможно ли рассчитать площадь параллелограмма по диагоналям, длины которых
равны 6 см и 4 см? При этом известно, что образованный ими угол является
прямым.
Для определения площади параллелограмма через известные длины проведенных
в нем диагоналей применяется приведенная ниже формула:
S = ½*d 1*d 2*sin α,
где диагонали фигуры обозначены как d 1 и d 2, а синус образованного в
результате их пересечения угла – sin α.
Подставим в указанное равенство величины, приведенные в задании:
S = 1/2 * 4 см * 6 см * sin 90° = 12 см кв.
Ответ: Площадь параллелограмма, вычисленная через диагонали, равна 12 см
кв.
На одной из сторон параллелограмма ABCD, обозначенной как ВС, отмечена точка
М. Чему будет равна площадь параллелограмма при условии, что площадь
треугольника МАD составляет 21 см кв.?
Под площадью параллелограмма (S) понимается величина, полученная в
результате умножения длины его стороны (b) на высоту (h), которая опущена
к ней. В виде формулы это выглядит следующим образом:
S =b*h
Площадь треугольной фигуры представляет собой ½ числа, полученного
произведением длины стороны на высоту, которая к ней проведена:
S=1/2*b*h,
Отсюда получаем, что:
b*h=2Sт=2*21=42 см кв.
Если говорить о треугольнике МАD, то в нем сторона АD представлена в
качестве стороны b, как и в случае с параллелограммом. Высота указанного
треугольника будет также представлять собой высоту параллелограмма. Это
обусловлено тем, что точка М расположена на стороне, которая
противоположна стороне ВС. Из этого следует, что площадь параллелограмма
равна 42 см кв.
Ответ: Площадь параллелограмма равна 42 см кв.
Параллелограмм ABCD имеет стороны длиной 10 см и 14 см, а также острый угол
в 60 градусов. Каким образом можно вычислить площадь параллелограмма?
В параллелограмме ABCD нужно провести высоту ВН на сторону AD. После этого
получается треугольник АВН с углом в 90 градусов. Можно рассчитать, чему
равен еще один угол данного треугольника:
АВН = 90-60 = 30
ВН = АВ*sin60 = 10*корень3/2 = 5*корень3
Таким образом, можно узнать, чему будет равна площадь параллелограмма:
S = AD*ВН = 14*5*√3 = 70*√3 см кв.
Ответ: Площадь параллелограмма составляет 70*√3 см кв.
Дан параллелограмм, через середины пары смежных сторон которого проведена
прямая. Она отсекает треугольную фигуру площадью 32 см кв. Чему в данном
случае равна площадь параллелограмма?
АС представляет собой диагональ биссектрисы. В этом случае оба
треугольника FMD и ADC являются подобными по той причине, что они имеют
общий угол А и их стороны равны. Из этого следует, что:
S ADC = 1/2*ab*sina
S FDM=1/2 *2a*2bsina
Отношение площадей двух треугольников выглядит как:
S ADC / S FDM= 32/x
1/4=32/x
x=128
Теперь можно высчитать площадь параллелограмма:
S = 128*2 = 256 см кв.
Читать дальше: как найти площадь трапеции.
Смежные углы в геометрии
15 июня 2022
Два угла называются смежными, если у них общая вершина, общая сторона, а две других стороны образуют прямую.
В этом уроке:
- Что такое смежные углы
- Основное свойство смежных углов
- Биссектрисы смежных углов
- Тренировочные задачи
Это довольно простая, но очень важная тема.
1. Что такое смежные углы
Возьмём прямую $AB$ и отметим на ней точку $M$. Получим развёрнутый угол $AMB:$
Проведём из точки $M$ луч $MN$, не совпадающий с лучами $MA$ и $MB$.
Получим два новых угла: $angle AMN$ и $angle BMN$. Эти углы и называются смежными.
Определение. Два угла называются смежными, если у них одна общая сторона, а две других образуют прямую (или, что то же самое, являются дополнительными лучами).
Обратите внимание: чтобы углы стали смежными, им недостаточно просто иметь общую сторону. Вот эти углы — не смежные, хотя они и имеют общую сторону:
А вот дальше — смежные, хотя и расположены немного непривычно:
Часто смежные углы возникают в точке пересечения прямых. Например, при пересечении двух прямых
образуется четыре пары смежных углов: $angle ASM$ и $angle ASN$; $angle BSM$ и $angle MSN$; $angle ASN$ и $angle BSN$; наконец, $angle ASM$ и $angle BSM$.
2. Основное свойство внешних углов
У смежных углов есть замечательное свойство, которое будет преследовать нас на протяжении всей геометрии, до конца 11 класса.
Теорема. Сумма смежных углов равна 180°.
Доказательство. Рассмотрим смежные углы $AMN$ и $BMN$ с общей стороной $MN$:
Поскольку луч $MN$ делит угол $AMB$ на смежные углы $AMN$ и $BMN$, по основному свойству углов
[angle AMB=angle AMN+angle BMN]
Но угол $AMB$ — развёрнутый, поэтому
[angle AMN+angle BMN={180}^circ ]
Другими словами, если один угол равен $alpha $, то смежный с ним равен ${180}^circ -alpha $. Или если известно, что углы $alpha $ и $beta $ — смежные, то $alpha +beta ={180}^circ $.
Казалось бы, элементарные рассуждения, но их вполне достаточно, чтобы решать большой класс задач.
Задача 1. Найдите угол, смежный с углом $ABC$, если:
- $angle ABC={36}^circ $.
- $angle ABC={121}^circ $.
Решение
1) Обозначим смежный угол $DBC=x$. Он будет тупым:
Тогда $x=180-36=144$.
2) Обозначим смежный угол $DBC=x$. Он будет острым:
Тогда $x=180-121=59$.
Немного усложним задачу.
Задача 2. Найдите смежные углы, если:
- один из них на 68° больше другого.
- один из них в 5 раз больше другого.
- их градусные меры относятся как 5 : 4.
Решение.
1) Пусть один из углов равен $x$. Тогда другой (очевидно, больший) будет равен $x+68$.
Поскольку углы смежные, их сумма равна 180 градусов:
[begin{align}2x+68&=180 \ 2x&=112 \ x&=56 end{align}]
Итак, один угол равен 56 градусов. Тогда другой равен $x+68=124$ градуса.
2) Пусть меньший угол равен $x$. Тогда смежный с ним равен $5x$.
Сумма смежных углов равна 180 градусов, поэтому
[begin{align}5x+x&=180 \ 6x&=180 \ x&=30 end{align}]
Мы нашли меньший угол — он равен 30 градусов. Тогда второй угол равен $5x=150$ градусов.
3) В задачах с отношениями величинам удобно обозначать их кратными некоторой переменной. Например, если углы относятся как 5 к 4, то пусть величина одного угла будет $5x$, а другого — $4x$.
Сумма смежных углов вновь равна 180 градусов:
[begin{align}5x+4x&=180 \ 9x&=180 \ x&=20 end{align}]
Поэтому сами углы равны $4x=80$ и $5x=100$ градусов.
3. Биссектрисы смежных углов
Вновь рассмотрим смежные углы $AMN$ и $BMN$:
Построим биссектрису $MC$ угла $AMN$ и биссектрису $MD$ угла $BMN$:
Если $angle AMC=x$ и $angle BMD=y$, то $angle AMN=2x$ и $angle BMN=2y$. Это смежные углы, поэтому
[begin{align}2x+2y&={180}^circ \ x+y&={90}^circ end{align}]
Получается, что биссектрисы смежных углов всегда пересекаются под углом 90°. Этот факт известен далеко не всем ученикам. Хотя он вполне может встретиться, например, на ЕГЭ.
Задача 3. Углы $ABC$ и $MBC$ смежные, $angle ABC={70}^circ $. Луч $BD$ принадлежит углу $ABC$, причём $angle ABD={40}^circ $. Найдите угол между биссектрисами углов $CBD$ и $MBC$.
Решение. Изобразим все углы на рисунке:
Видим, что углы $ABD$ и $MBD$ — смежные. Следовательно
[begin{align}angle MBD&={180}^circ -angle ABD= \ &={180}^circ -{40}^circ ={140}^circ end{align}]
Синим цветом отмечены биссектрисы углов $CBD$ и $MBC$. Обозначим величину углов переменными: $angle CBD=2x$, $angle MBD=2y$. Но $angle MBD=angle MBC+angle CBD$, поэтому
[begin{align}2x+2y&=140 \ x+y&=70 end{align}]
Это и есть искомый угол между биссектрисами. Он равен 70 градусов.
Задача 4. Дан треугольник $ABC$. Лучи $AM$ и $CN$ лежат на одной прямой со стороной $AB$ (см. рисунок). Известно, что $angle MAC+angle ABC={180}^circ $. Докажите, что $angle MAC=angle NBC$.
Пусть $angle ABC=x$. Тогда из условия следует, что $angle MAC={180}^circ -x$.
С другой стороны, углы $ABC$ и $NBC$ смежные, поэтому $angle NBC={180}^circ -x$.
Получается, что углы $MAC$ и $NBC$ равны одному и тому же выражению. Следовательно, $angle MAC=angle NBC$, что и требовалось доказать.
Смотрите также:
- Что такое вертикальные углы

- Перпендикулярные прямые — определение и свойства

- Правила комбинаторики в задаче B6

- Метод координат в пространстве

- Четырехугольная пирамида: как найти координаты вершин

- Задача B4 про три дороги — стандартная задача на движение















