Как найти площадь смоченного сечения канала

The perimeter of the wet cross sectional area is known as the wetted perimeter. It depends on the hydraulic diameter or hydraulic radius. The term is commonly used in fields like civil engineering, environmental engineering, hydrology, geomorphology, and in heat transfer applications. The hydraulic radius for a circular pipe flowing full is easy to calculate. Here is an online mechanical calculator to calculate the wetted perimeter of a circular hydraulic pipe channel.

The perimeter of the wet cross sectional area is known as the wetted perimeter. It depends on the hydraulic diameter or hydraulic radius. The term is commonly used in fields like civil engineering, environmental engineering, hydrology, geomorphology, and in heat transfer applications. The hydraulic radius for a circular pipe flowing full is easy to calculate. Here is an online mechanical calculator to calculate the wetted perimeter of a circular hydraulic pipe channel.

В
гидравлических расчётах для характеристики
размеров и формы поперечного сечения
потока вводят понятие о живом
сечении и его элементах: смоченном
периметре и гидравлическом радиусе.

Живым
сечением
называется поверхность в пределах
потока, проведённая нормально к линиям
тока.

Для
круглого трубопровода, когда всё
поперечное сечение заполнено жидкостью,
живым сечение является площадь круга:

(рис.3.6).

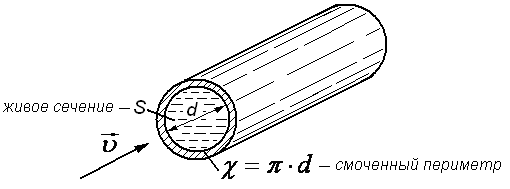
Рис.
3.6. Элементы потока

Смоченным
периметром
называют ту часть периметра живого
сечения, по которой жидкость соприкасается
со стенками трубопровода (рис.3.6).
Смоченный периметр обычно обозначают
греческой
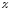(хи). Для круглой трубы полностью
заполненной жидкостью смоченный периметр
равен длине окружности:

.

Гидравлическим
радиусом
называют отношение живого сечения к
смоченному периметру, т.е. величину

.

Эта
величина характеризует удельную, т.е.
приходящуюся на единицу длины смоченного
периметра, площадь живого сечения. Легко
сделать вывод, что поток с наибольшим
гидравлическим радиусом при прочих
равных условиях имеет минимальную силу
трения, приложенную к смоченной
поверхности.

Для
круглых труб, полностью заполненных
жидкостью, гидравлический радиус равен
четверти диаметра:

.

Введение
гидравлического радиуса как характерного
размера позволяет сравнивать по критерию
подобия (Re)
потоки с разными формами живого сечения.

Рассмотренные
основные понятия позволяют решать самые
различные практические задачи гидравлики.

Пример
3.1. Определить
скорость потока в трубопроводе. Диаметр
,
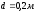расход воды (несжимаемой жидкости) –.

Решение.
Искомая скорость
.

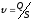Определим
площадь живого сечения:

.

Скорость
потока:

.

3.6. Уравнение количества движения для потока жидкости

Гидравлика
– это техническая механика жидкости,
в которой часто используются упрощённые
методы для решения инженерных задач.
Во многих случаях при решении практических
задач гидравлики удобно применять такие
центральные понятия механики, как
количество движения (уравнение импульсов)
и кинетическая энергия.

В
связи с этим необходимо рассмотреть
возможность вычисления количества
движения и кинетическую энергию потока
жидкости по средней скорости, а не по
действительным местным скоростям. Это
позволит существенно упростить
гидравлические расчёты.

Для
материального тела массой
,
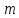движущегося со скоростью,
изменение количества движения за времявследствие действия силывыразится векторным уравнением

, (3.7)

где
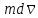– приращение количества движения,
обусловленное импульсом.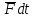

Жидкость
представляет собой материальную систему,
поэтому основной закон механики может
быть приложен к любой выделенной из неё
массе.

Применим
эту теорему механики к участку потока
жидкости с расходом
между сечениями 1-1 и 2-2 (выделенный
участок заштрихован). Ограничимся
рассмотрением только установившегося
движения жидкости (рис. 3.7).

За
время
этот участок переместится в положение,
определяемое сечениям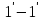ии.
Объёмы этих элементов,
а, следовательно, и их массыодинаковы, поэтому приращение количества
движения будет равно

. (3.8)

Это
приращение количества движения
обусловлено импульсом всех внешних
сил, действующих на объём жидкости между
сечениями 1-1 и 2-2. Внешними силами,
приложенными к выделенному объёму,
являются сила тяжести всего объёма
,
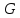силы давления в первом и втором сечениях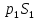и(нормальные к этим сечениям и направленные
внутрь объёма), а также реакции стенок
трубы,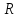
которая складывается из сил давления
и трения, распределённых по боковой
поверхности объёма.

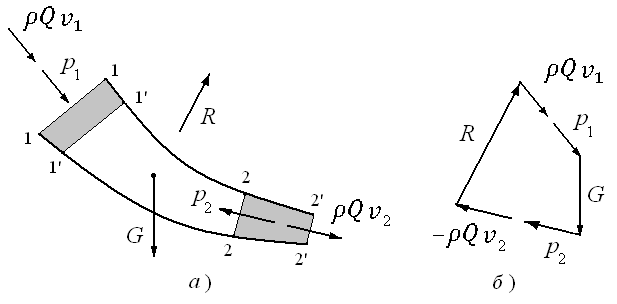
Рис.
3.7. Применение уравнения количества
движения

к
потоку жидкости

Уравнение
импульсов (3.7) для рассматриваемого
случая можно записать в виде

.

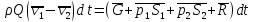После
сокращения на

. (3.9)

Составив
проекции этого векторного уравнения
на три координатные оси, получим три
алгебраических уравнения с тремя
неизвестными –
.

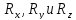Л.
Эйлер предложил удобный графический
способ нахождения силы
.
Перенося в формуле (3.?) все слагаемые в
одну сторону, можно представить его в
виде суммы векторов:

=
0, (3.10)

где
вектор
взят с обратным знаком (т.е. по направлению
обратный действительному). В соответствии
с этим выражением (3.10) силу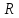можно найти, построив замкнутый
многоугольник сил, как это показано на
рис. 3.7,а.

Анализ
показывает, что при вычислении количества
движения и кинетической энергии по
средней скорости допускается ошибка,
которую можно учесть с помощью двух
коэффициентов:

–
коэффициента Буссинеска
при вычислении количества движения;

–
коэффициента Кориолиса
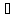в уравнении Бернулли при вычислении
кинетической энергии.

Величина
обоих коэффициентов зависит от характера
распределения скоростей в поперечном
сечении потока жидкости. На практике
при турбулентном режиме движения
коэффициент Кориолиса
, а коэффициент Буссинеска.
Поэтому обычно полагают.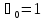
Однако встречаются отдельные случаи,
когдадостигает больших значений, и тогда
пренебрежение им может привести к
значительным погрешностям.

Пример
3.2. Определить
силу воздействия потока жидкости на
преграду. Пусть жидкость вытекает в
атмосферу и наталкивается на безграничную
стенку, установленную нормально к
потоку. В результате жидкость растекается
по стенке, изменяя направление своего
течения на 90⁰
(рис.
3.8). Известны площадь сечения потока
,
скорость истеченияи плотность жидкости.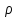

Рис. 3.8. Воздействие
струи на преграду

Для
решения данной задачи берём фиксированный
объём, показанный штриховой линией, и
применяем теорему Эйлера. Так как
давление внутри струи и по поверхности
жидкости равно атмосферному, т.е.
избыточное давление равно нулю, уравнение,
выражающее теорему Эйлера, для направления,
совпадающего с вектором скорости
истечения
,
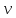будет иметь вид

,

или . (3.11)

Это
и есть сила воздействия потока жидкости
на преграду. При другом угле установке
стенки или других её форме и размерах
в правую формулы (3.11) вводится безразмерный
коэффициент, отличный от единицы, но
пропорциональность силы
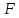произведениюсохранится.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Расчет канала трапецеидального поперечного сечения

Страницы работы

Содержание работы

Санкт-Петербургский государственный политехнический университет

Задание № 4 по курсу гидравлики

«Расчет канала трапецеидального поперечного сечения»

Выполнил студент гр. 3013/2: Кулакова М.Н.

1. Расчет канала на равномерное движение 2

1. 1. Определение глубины равномерного движения h_o1 и ширины канала по дну b на подводящем участке канала при β=(β_г.н.)_пред.. 2

2. 1. Определение глубины равномерного движения на отводящем участке канала h_o2 , полагая ширину канала b, равной найденной в п.1. 7

3. Определение средних скоростей движения воды в канале и сравнение их с максимально допустимыми для заданного грунта скоростями. 10

2. Расчет каналов на неравномерное движение 12

2.1. Определение критической глубины и критического уклона 12

2.2. Построение графика удельной энергии сечения 14

2.4. Построение кривых свободной поверхности на отводящем участке канала 21

3.1. Построение графика прыжковой функции 27

3.2. Построение линии сопряженных глубин для кривой типа и определение местоположения прыжка 28

3.4. Определение длины гидравлического прыжка и потери энергии в нем 29

1. Расчет канала на равномерное движение

1. 1. Определение глубины равномерного движения h_o1 и ширины канала по дну b на подводящем участке канала при β=(β_г.н.)_пред..

Поперечное сечение трапецеидального канала, в котором при заданных Q, n, m, i средняя скорость максимальна, а площадь поперечного сечения и смоченный периметр минимальны, называется гидравлически наивыгоднейшим. В строительной практике удобной характеристикой такого сечения является относительная ширина:

где b-ширина канала по дну; h – глубина потока; m – коэффициент бокового откоса.

Подставляя значение m = 2, 3получим:

Из геометрических соображений для трапецеидального канала легко найти следующие зависимости:

площадь поперечного сечения ω = (b+mh)h;

ширина потока на уровне свободной поверхности B = b+2mh;

смоченный периметр χ = b+2h√1+m 2 ;

гидравлический радиус R = ω/ χ;

коэффициент Шези C = R 1/6 /n;

Далее для подводящего участка следует найти необходимый модуль расхода :

,

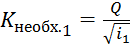где 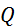— расход воды в канале, равный 44,2 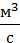, а 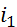– уклон дна подводящего участка канала, равный 0,0005.

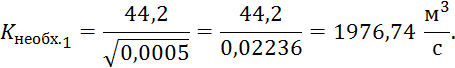
Глубину 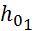равномерного движения на подводящем участке канала определяем методом подбора. Задаёмся неизвестной величиной и вычисляем все необходимое. Значение глубины выбираем произвольно. Для удобства построим таблицу.

Источник

Поперечный профиль каналов

Чаще всего каналы имеют трапециидальную форму поперечного сечения.

Рис. 3.24. Поперечный профиль канала

Поперечным профилем канала называется линия ABCD, пересечения канала с плоскостью, перпендикулярной к направлению сечения. Часть MBCN этого профиля, находящегося под водой, называется смоченным периметром. Его длина обозначается греческой буквой χ (произносится «хи»). Смоченный периметр – это часть периметра живого сечения водотока, соприкасающаяся со стенками и дном русла. Он равен

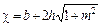(3.3)

где m – коэффициент откоса (величина характеризующая крутизну откоса);

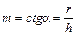, (3.4)

где r – заложение откоса; h – глубина воды в канале.

Площадь MBCN, занятая водой называется живым сечением канала и обозначается буквой ω (омега).

где b – ширина канала по дну. Ширина канала на уровне воды

l– длина откоса. 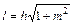. (3.7)

Сила трения жидкости о смоченную поверхность зависит от ее площади. Чем больше смоченная поверхность, тем больше при прочих равных условиях сила трения. Для оценки этого влияния в гидравлике широко используется понятие гидравлического радиуса.

Отношение площади живого сечения ω к длине смоченного периметра χ называется гидравлическим радиусом сечения и обозначается буквой R, т.е.

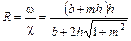(3.8)

Эта величина характеризует удельную, т.е. приходящуюся на единицу длины смоченного периметра, площадь живого сечения. Поток с наибольшим гидравлическим радиусом при прочих равных условиях имеет минимальную силу трения, приложенную к смоченной поверхности (R ® max при c ® min).

Чем больше смоченная поверхность, тем больше при прочих равных условиях сила трения. Для оценки этого влияния в гидравлике широко используется понятие гидравлического радиуса R. Легко сделать вывод, что поток с наибольшим гидравлическим радиусом при прочих равных условиях имеет минимальную силу трения, приложенную к смоченной поверхности.

Количество протекающей в единицу времени по каналу воды Q (расход) определяется уравнением

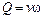, (3.9)

причем скорость течения v в свою очередь определяется формулой Шези

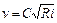, (3.10)

где С – коэффициент скорости, зависящий от шероховатости русла;

i – уклон дна канала, равный уклону поверхности потока (равномерное движение). Подставив выражение скорости потока из формулы Шези в формулу расхода получим:

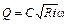. (3.11)

Из этой формулы следует, что при данной площади живого сечения ω тот канал пропустит больший расход, у которого при данном уклоне больше гидравлический радиус.

Из формулы R = ω/χ следует, что R ® max при c ® min. Канал такого профиля будет обладать при прочих равных условиях наибольшей пропускной способностью, или иначе сказать, профиль такого канала будет гидравлически наивыгоднейшим.

Как известно из геометрии, из всех фигур минимальным периметром при одной и той же площади обладает круг.

Среди безнапорных потоков таким свойством обладает поток полукруглого сечения (рис. 3.25) гидравлический радиус, которого равен

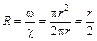(3.12)

Далее из всех четырехугольных профилей, наивыгоднейшим профилем обладает половина правильного шестиугольника с углом наклона боков к горизонту под углом 60°. Глубина такого канала h = 0,866b, а m = 0,57. Менее выгодным является прямоугольник, как половина квадрата, у которого b = 2h. Можно показать, что и в этих случаях гидравлический радиус равен половине глубины потока[6].

Рис.3.25. Поперечное сечение потоков с гидравлически наивыгоднейшим профилем

На практике выполнение канала такого сечения встречает большие трудности из-за низкой устойчивости боковых поверхностей. Необходимо специальное крепление и т.д. В обыкновенных условиях канал выполняется в виде трапеций с боковыми гранями не круче угла естественного откоса данного грунта, т.к. иначе они будут осыпаться независимо от размывания канала водой.

При трапецеидальном поперечном профиле канала живое сечение канала будет наивыгоднешим в том случае, если соотношение между шириной по дну b и глубиной наполнения h будет

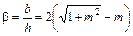, площадь живого сечения ,

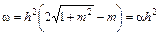а глубина воды в канале 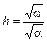, т.е. гидравлический наивыгоднейший профиль останется только для расчетной глубины наполнения. При всех других наполнениях выгодность такого профиля утрачивается.

В осушительных каналах приходиться считаться с большими колебаниями уровней воды, исключающими возможность применения гидравлически выгодных сечений.

Форма поперечного сечения проводящих и оградительных каналов – трапециидальная. Если канал проходит в разных грунтах, то поперечное сечение канала имеет сложный профиль. Откос такого канала имеет переменный коэффициент заложения откосов (рис.3.26).

Разрешается только один перелом откосов. Верхний откос не должен быть положе нижнего.

Рис. 3.26)Схема поперечного сечения канала сложного профиля.

При мощности торфа до 0,7 м перелом откоса не предусматривают.

Ширина проводящих и оградительных каналов по дну определяется расчетом, но не должна быть менее ширины по дну нерасчетных каналов: 0,5 – 0,7 м для магистрального канала; 0,5 м – для валовых; 1,0 м – для оградительных.

Ширину по дну и коэффициент заложения откосов картовых каналов назначаются с учетом принимаемых для строительства и эксплуатации машин (табл.3.7) [7]/

Ширина по дну и коэффициент откоса картовых каналов в зависимости от применяемой для строительства машины

Наименование машин	Ширина по дну, b, м	Коэффициент заложения откосов m
Торфяной экскаватор с профильным ковшом	0,3	0,32
Торфяной экскаватор со штатным ковшом	0,45	0,27(до h = 1,38 м, выше m = 0)
Машина для предварительного осушения (типа МТП-37)	0,1	0,375
Машина непрерывного действия (типа МТП-32А)	0,2	0,25

Дата добавления: 2021-03-18 ; просмотров: 301 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Смачиваемая площадь треугольного сечения канала Калькулятор

Search
Дом	Инженерное дело ↺
Инженерное дело	Гражданская ↺
Гражданская	Гидравлика и гидротехнические сооружения ↺
Гидравлика и гидротехнические сооружения	Поток в открытых каналах ↺
Поток в открытых каналах	Практические разделы канала ↺

Смачиваемая площадь треугольного сечения канала Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Глубина потока: 3.3 метр –> 3.3 метр Конверсия не требуется
Тета: 30 степень –> 0.5235987755982 Радиан (Проверьте преобразование здесь)

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

24.5640239606895 Квадратный метр –> Конверсия не требуется

8 Практические разделы канала Калькуляторы

Смачиваемая площадь треугольного сечения канала формула

Площадь смачиваемой поверхности = (Глубина потока^2)*(Тета+cot(Тета))

S = (d_f^2)*(θ+cot(θ))

Что такое смоченная область?

Площадь поверхности, которая взаимодействует с рабочей жидкостью или газом. При использовании на море смоченная область – это часть корпуса, погруженная в воду. В аэронавтике смоченная область – это область, которая контактирует с внешним потоком воздуха. Это имеет прямое отношение к общему аэродинамическому сопротивлению самолета.

Гидравлический диаметр (эквивалентный диаметр) —

это отношение учетверенной площади живого сечения потока к смоченному периметру.

Общие сведения

Гидравлический диаметр (эквивалентный диаметр) обычно обозначается — d_г, d_h, D_г. Широко применяется при гидравлических и аэродинамических расчетах различных систем, где формой сечения каналов не является окружность.  Гидравлический (эквивалентный) диаметр может служит мерой эффективности системы в пропускании потока жидкости или газа.

Формулы расчет гидравлического диаметра (эквивалентного диаметра). Калькуляторы гидравлического диаметра (эквивалентного диаметра).

Классическая формула гидравлического диаметра (эквивалентного диаметра)

D_г=(4*S)/P,

где S— площадь поперечного сечения потока жидкости или газа; P — смоченный периметр поперечного сечения потока.

Гидравлический диаметр (эквивалентный диаметр) круглого сечения (например: воздуховоды, трубы, дымоходы и т.п)

Совпадает с геометрическим диметром, т.е. D_г=D_вн, где D_вн — внутренний диаметр круглого сечения воздуховода, трубы и т.п.

Гидравлический диаметр (эквивалентный диаметр) сечения в виде кольца (например: труба в трубе и т.п.)

D_г=2(r₂-r₃),

где r₂— внутренний радиус внешней трубы, воздуховода и т.п.; r₃ — внешний радиус внутренний трубы, воздуховода и т.п.

Гидравлический диаметр (эквивалентный диаметр) прямоугольного сечения (например: трубы квадратного сечения,  дымоходы и т.п.)

D_г=2*a*b/(a+b),

где a— первая сторона прямоугольного сечения; b — вторая сторона прямоугольного сечения.

Видеоматериал по теме «Гидравлический диаметр (эквивалентный диаметр)»

Примечание

Смоченный периметр —

длина части границы канала, касающейся жидкости.

Поделиться ссылкой: