3
Ребята помогите! Надо нарисовать снеговика и узнать площадь всех кругов снеговика,даже рук и ног! Помогите или переведите свои о
Ребята помогите!
Надо нарисовать снеговика и узнать площадь всех кругов снеговика,даже рук и ног!
Помогите или переведите свои ответы(варианты).
Заранее благодарю вас)
1 ответ:
0
0
Площадь круга – . Когда вы рисуете снеговика, вы же знаете, какой радиус у вашей окружности. Допустим, голова будет радиусом 5 см, тело – 7 см, нижняя часть – 10 см. Руки и ноги по 1 см, тогда площадь любого круга вы сможете найти, подставив значение радиуса вместо R. (Брать мои числа не обязательно, берите любые, главное, знать, какое берёте)
Читайте также
во втором куске а:4 метров ткани.
Ответ:
17) =4+0.5x=-2
0.5x=-2-4
0.5x=6
x=6/0.5
X=12 B)
18)= x-1.8=1/3
x=1/3+1.8
X=9под корнем 9
x=9 С)
Х=81-34
х=47
47х=186
х=4
1) 11+13=24 – куртки сшили всего
2) 72:24=3 – метра ткани нужно на 1 куртку
3) 3*11=33 – метра израсходовали во вторник
4) 3*13=39 – метров израсходовали в среду
Все просто)
15*4=60 кв.м – площадь пола
1 кв.м = 100 кв.дм
60 кв.м = 6000 кв.дм
10*10 = 100 кв.дм – площадь одной плитки
6000:100 = 60 штук
60 БАЛЛОВ!!! СРОЧНО!!!Составить алгоритм нахождения площади фигуры.(снеговик, состоящий из трех кругов)
R1=2
R2=3
R3=4
Дарья Имыкина
Вопрос задан 21 сентября 2019 в
5 – 9 классы,
Информатика.
-
Комментариев (0)
Добавить
Отмена
Идеальные пропорции, которыми должен обладать снеговик, вычислили с помощью сложной формулы математики из Университета Ноттингем Трент (Великобритания).
Формула учитывала такие характеристики, как температура на улице, чистота и свежесть снега, используемого для снеговика, количество и диаметр снежных шаров, из которых он состоит, высота получившейся фигуры, а также правильное расположение глаз и длину носа-морковки.
В итоге ученые рассчитали, что каждый из трех снежных шаров должен иметь строго определенный диаметр. Самый маленький шар (голова) — 30 см, средний шар — 50 см, а самый большой — 80 см. В итоге получится фигура высотой 1,62 метра.
Для двух «рук» снеговика стоит использовать четыре палочки — по две на каждую. Глаза следует расположить на расстоянии не больше 5 см друг от друга и взять морковку для носа длиной ровно 4 см. Лучше всего использовать только что выпавший снег, его температура должна составлять 0 °C или ниже.
Источник
gherit541
Вопрос по информатике:
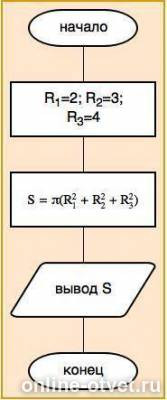
60 БАЛЛОВ!!! СРОЧНО!!!Составить алгоритм нахождения площади фигуры.(снеговик, состоящий из трех кругов)
R1=2
R2=3
R3=4
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
kermusthate
Блок-схема во вложении
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Информатика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Информатика — наука о методах и процессах сбора, хранения, обработки, передачи, анализа и оценки информации с применением компьютерных технологий, обеспечивающих возможность её использования для принятия решений.
Тема: Длина окружности и площадь круга.
Цели урока:
– Вспомнить понятия окружности, круга и их элементов, изучить формулу длины окружности, применять ее при решении задач, получать значение числа в ходе выполнения практической работы;
– развивать познавательный интерес учащихся, познакомить их с историческим материалом;
– прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности.
Оборудование: циркуль, карандаши, таблицы, индикаторы настроения, картинки, картонные кружки разных размеров, нитка.
Ход урока.
1.Организационный момент.
Здравствуйте, садитесь! Проверяем готовность к уроку.
2. Мотивация урока. (слайд 1)
Попробуйте отгадать загадку.
Нет углов у меня,
И похож на блюдце я,
На тарелку и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья? (Круг)
У круга есть одна подруга,
Знакома всем ее наружность!
Она идет по краю круга
И называется -…(окружность)
Да, именно эти фигуры нам понадобятся сегодня.
3. Изучение нового материала.
3. Упражнение на развитие внимания «Стоп – игра!»
Учитель говорит понятия и поочерёдно показывает несколько карточек с изображением окружности и отрезков. Ученики пишут в тетрадях название тех отрезков, которые соответствуют понятию. Учитель говорит: «Стоп игра!», учащиеся ставят в тетради вертикальную черту. Учитель говорит следующее понятие и показывает те же карточки, ученики продолжают писать
после черты.
Давайте сделаем вывод и «соберем» разбежавшиеся правила.
Начало:
Окружность – замкнутая линия без самопересечений…
Круг – это часть плоскости,…
Радиус – это отрезок, соединяющий…
Диаметр – это отрезок, соединяющий…
Хорда – это отрезок, соединяющий…
Диаметр – это хорда,…
Конец:
…все точки которой находятся на одинаковом расстоянии от центра.
…ограниченная окружностью.
…две точки окружности.
…проходящая через центр.
…соединяющий центр окружности с любой точкой на окружности.
…две точки окружности и проходящий через центр.
Из истории.
Недаром древние греки считали окружность совершеннейшей и «самой круглой» фигурой. И в наши дни в некоторых ситуациях, когда хотят дать особую оценку, используют слово «круглый», которое считается синонимом слова «полнейший»: круглый отличник, круглый сирота и т.п.
Также считают и колесо – одно из самых замечательных изобретений человека.
Наверное, весь секрет кроется в свойствах удивительной линии – окружности.
Окружность – самая простая кривая линия. Радиус – происходит от латинского слова «радиус» – «спица колеса». Хорда – греческое слово и переводится – «струна». Диаметр – «диаметрос» – тоже греческое слово, переводится – «поперечник».
Скажите, а с помощью какого инструмента мы можем построить окружность?
Загадка
Танцевальное движенье
Совершеннейшей ноги
И круги, круги, круги
Вызывают восхищенье.
Балерина создавала
Точный круг в один момент,
Подивился ей немало
Достославный геометр.
О прекрасной балерине
Вспоминал частенько он
Не по этой ли причине
… был изобретён.
(Циркуль)
Из истории возникновения циркуля.
Циркуль от латинского слова “circulus” – круг, окружность (“circa” – вокруг, кругом, то есть цирк – это круг)
Сейчас уже нельзя сказать, кто именно изобрел этот инструмент – история не сохранила для нас его имя, но легенды Древней Греции приписывают авторство Талосу, племяннику знаменитого Дедала, первого «воздухоплавателя» древности. История циркуля насчитывает уже несколько тысяч лет – судя по сохранившимся начерченным кругам, инструмент был знаком еще вавилонянам и ассирийцам (II – I века до нашей эры). На территории Франции, в галльском кургане был найден железный циркуль (I век нашей эры), во время раскопок в Помпеях было найдено много древнеримских бронзовых циркулей.
Напомню, что обозначить r – радиус, а d – диаметр, тогда: d=2 r.
Я тоже для вас приготовила шарики (картонные кружочки разных радиусов разных цветов, по 3 на одну парту).
Давайте измерим длину каждой окружности. В чем трудность? Да, к сожалению, специального прибора для измерения длины окружности нет. Но и это не останавливало человека. Предложите свой способ измерения длины окружности (обсуждение в группах).
Еще древние греки умели находить длину окружности по формуле
С = π d или С = 2πr , где d – диаметр окружности, а – радиус окружности.
А что это за число π?
4. Первичное закрепление нового материала.
Практическая работа с раздаточным материалом «Круги».
( из картона выполнены круги разного диаметра, к которым прикреплена нить, предназначенная для измерения длины окружности.)
-Возьмите в руки круг. Что на нём отмечено? (Радиус, диаметр)
-Измерьте линейкой диаметр. Результат измерений запишите в тетрадь.
-Как вы думаете, для чего нужна нить?
-Измерьте нитью длину окружности, приложите к линейке, результат измерения запишите в таблицу:
|
№ опыта |
Длина окружности (С) |
Диаметр (d) |
Значение π =С: d |
|
1 |
|||
|
2 |
|||
|
3 |
-Найдите с помощью калькулятора отношение длины окружности к диаметру.
-Поднимите руки те, у кого число получилось больше трёх, но меньше четырёх.
Независимо от того, какого диаметра взят круг, отношение длины окружности к диаметру будет больше трёх, но меньше четырёх. Запишите в тетрадь двойное неравенство: 3 < p < 4.
Более точные вычисления дают бесконечную десятичную дробь.
Демонстрация плаката с числом p с 24-мя знаками после запятой (слайд 2)
≈ 3,141592653589793238462643….)
Математики договорились обозначать это число первой буквой греческого слова «Периферия» – p (пи). На некоторых кругах есть кармашек. Достаньте его содержимое и прочитайте вслух исторические сведения.
– Первым обозначение p (пи) ввёл в1706 году английский математик Джонс.
– Французский математик Франсуа Виет нашёл значение p (пи) с девятью десятичными знаками
– В 1988 году японский учёный Ясума Канеда вычислил с помощью ЭВМ 400 миллионов цифр после запятой.
– в настоящий момент Японские ученые вычислили Пи с рекордной точностью. Новый рекорд составляет 2576980377524 (2 триллиона 576 миллиардов 980 миллионов 377 тысяч 524) знака.
Из истории.
Еще в древности людям были известны многие геометрические фигуры, в том числе окружность и круг. Об этом свидетельствуют археологические раскопки. Еще тогда приходилось решать задачи на вычисление длины окружности. Сейчас известно, что значением числа π в разные времена считали различные числа. Так, в Древнем Египте (ок. 3500 лет назад) считали π = 3,16; древние римляне полагали, что π= 3,12. Все эти значения были определены опытным путем. Великий ученый Древней Греции Архимед определил, что значение π находится в следующих пределах 3<π<3
. Легенда гласит, что когда древнегреческий город Сиракузы, где жил в своё время Архимед, захватили римляне, учёный, занимаясь научными исследованиями, чертил окружности на песке. Солдату, который пришёл убить его, он воскликнул: “Убей меня, но не тронь моих кругов”.
С помощью современных электронно – вычислительных машин число «пи» было вычислено точностью до миллиона знаков после запятой. Для обозначения частного от деления длины окружности на диаметр впервые букву π использовал английский математик Джонс в 1706 г., но общепринятым это обозначение стало благодаря работам великого математика Эйлера. Он вычислил для числа я 153 десятичных знака.
5.Самостоятельная работа.
К нам пришли Колобок, Снеговик.
Давайте их нарисуем и вычислим с помощью формулы С = 2πr длину окружности и их площадь S= πr2 .
1) Рисуем колобка, окружность радиусом 4 см и разукрашиваем цветными карандашами.
2)Рисуем снеговика, радиусы окружностей которого 3 см, 4,5 см и 6 см. Затем разукрашиваем.
Из истории.
Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа π.
Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи» (англ. Pi Approximation Day), так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π.
Памятник числу «пи» на ступенях перед зданием Музея искусств в Сиэтле.
6. Итоги урока.
Д/з.
№868; №873 из учебника.
Задача: Ученики организовали соревнования по фигурному катанию на велосипедах. В этих соревнованиях нужно было проехать четыре круга по окружности радиусом 3 м. Какое расстояние проехали велосипедисты в этом виде фигурного катания?
Творческое задание: по возможности придумать стихотворную фразу для запоминания числа π.
Рефлексия.
Поставьте снеговику смайлик, на лице, с каким настроение Вы уходите с нашего урока.
Спасибо за урок. Урок закончен.

