Как найти площадь соприкосновения дощечки с камерой

На рисунке 113 изображена футбольная камера, соединённая с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на неё — гиря массой 5 кг. Высота столба воды в трубке 1 м. Определите площадь соприкосновения дощечки с камерой.

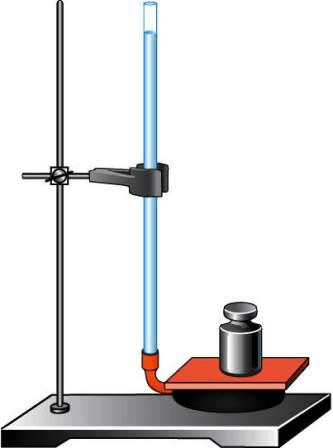
рис. 113

Страница 44 из 84

§40. Расчет давления жидкости на дно и стенки сосуда

Вопросы

1. Выведите формулу для расчёта давления жидкости на дно сосуда, имеющего форму прямоугольного параллелепипеда.

Ответ:

Нам необходимо найти силу, условно F, с которой жидкость, что налита в сосуд, давит на его дно. Она равна весу P жидкости, находящейся в сосуде, то есть F=P. А вес жидкости можно определить, зная массу m (P = gm). Массу можно вычислить по формуле m = ρV.
Сам объём жидкости, налитой в параллелепипед, легко рассчитать. Для этого необходимо знать величины всех его сторон. V = Sh (S – площадь основания,  h – высота).
Масса жидкости m = ρV, или m = ρSh.
Вес этой жидкости P = gm, или P = gρSh.
А мы знаем, что вес столба жидкости равен силе, с которой жидкость давит на дно сосуда. Тогда разделив вес P на площадь S, получим давление жидкости p:
$p=frac{P}{S}$ или $p=frac{gρSh}{S}$ или p = gρh

2. От каких величин и как зависит давление жидкости на дно сосуда?

Ответ:

P = gρh, где:
P − давление жидкости,
g = 9,8 Н/кг,
ρ − плотность жидкости,
h − высота столба жидкости.
Можно сделать заключение, что давление жидкости на дно сосуда зависит от плотности и высоты столба жидкости. 

3. По какой формуле рассчитывают давление жидкости на стенки сосуда, давление внутри жидкости?

Ответ:

Также как и итоговое значение давление, так и давление на стенки на определенной глубине будет рассчитываться по той же самой формуле. Разве что значение глубины будет другим. p = gρh (где − p − давление жидкости, g = 9,8 Н/кг, ρ − плотность жидкости, h − высота столба жидкости), так как давление на одной и той же глубине одинаково по всем направлениям.

Упражнение 17

1. Определите давление на глубине 0,6 м в воде, керосине, ртути.

Ответ:

Дано:
h = 0,6 м;
$ρ_{в}$ = 1000 кг/$м^{3}$;
$ρ_{к}$ = 800 кг/$м^{3}$;
$ρ_{рт}$ = 13600 кг/$м^{3}$;
$p_{в}$−?
$p_{к}$ − ?
$p_{рт}$−?
Решение:
$p = gρh$;
g ≈9,8 Н/кг;
$p_{в}$ = 9,8 * 1000 * 0,6 = 5880 Па;
$p_{к}$ = 9,8 * 800 * 0,6 = 4704 Па;
$p_{рт}$ = 9,8 * 13600 * 0,6 = 79968 Па ≈ 80 кПа
Ответ. 5880 Па, 4704 Па, 80 кПа.

2. Вычислите давление воды на дно одной из глубочайших морских впадин — Марианской, глубина которой 10 900 м. Плотность морской воды 1030 $кг/м^{3}$.

Ответ:

Дано:
h = 10 900 м;
ρ = 1030 кг/$м^{3}$.
p−?
Решение:
p = gρh;
g = 9,8 Н/кг;
p = 9,8 * 1030 * 10900 = 110024600 Па ≈ 110 МПа
Ответ. 110 МПа

3. На рисунке 113 изображена футбольная камера, соединённая с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на неё — гиря массой 5 кг. Высота столба воды в трубке 1 м. Определите площадь соприкосновения дощечки с камерой.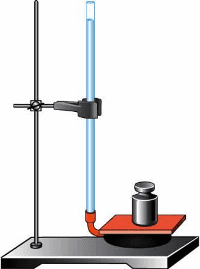

рис. 113

Ответ:

Дано:
m = 5 кг;
h = 1 м;
$ρ_{в} = 1000 кг/м^{3}$;
S−?
Решение:
$p_{1}=frac{F}{S}$ − давление гири на доску;
$p_{2}= gρh$ − давление столба воды в трубке.
Делаем заключение, если дощечка находится в равновесии, то давление на неё гири должно ровняться давлению водяного столба.
$p_{1}=p_{2}$;
F=gm;
$frac{gm}{S} =gρh$;
$S=frac{gm}{gρh} = frac{m}{ρh}$;
$S=frac{5}{1000 * 1}$ = 0,05 $м^{3}$.
Ответ. 0,05 $м^{3}$.

Задание

1. Возьмите высокий сосуд. В боковой поверхности его на разной высоте от дна сделайте три небольших отверстия. Закройте отверстия спичками и наполните сосуд водой. Откройте отверстия и проследите за струйками вытекающей воды (рис. 114). Почему вода вытекает из отверстий? Из чего следует, что давление увеличивается с глубиной?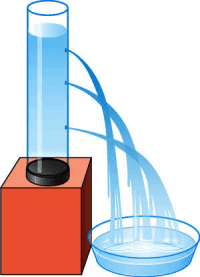

рис. 114

Ответ:

 Жидкость имеет свой вес и притягивается к земле. При этом при увеличении высоты столба жидкости, верхние слои с большим усилием давят на нижние. В итоге мы можем наблюдать, что через более низкие по уровню отверстия, жидкость вытекает с под большим давлением, струя сильнее, бьет дальше.

2. Налейте в стеклянный сосуд (стакан или банку) произвольное количество воды. Сделайте необходимые измерения и рассчитайте давление воды на дно сосуда.

Ответ:

Дано:
h = 0,15 м;
$ρ_{в}$ = 1000 кг/$м^{3}$;
p−?
Решение:
p = gρh;
g ≈ 9,8 Н/кг;
p = 9,8 * 1000 * 0,6 = 1470 Па;
Ответ. 1470 Па.

На рисунке изображена волейбольная камера, соединённая с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на неё — гиря массой 2 кг. Высота столба воды в трубке равна 0,5 м. Найди площадь соприкосновения дощечки с камерой. Ответ (округли до тысячных): площадь соприкосновения дощечки с камерой равна м2.
Прошу подробно! Даю 15 баллов!

Остались вопросы?

Новые вопросы по предмету Математика

Футбольная камера соединенная с вертикально расположенной стеклянной трубкой. В камере…

Как вы уже знаете, согласно закону Паскаля, давление в жидкостях распространяется одинаково во всех направлениях. Что же необходимо знать, чтобы рассчитать это давление? От чего зависит давление жидкости?

Взгляните на рисунок 1.

Как вы думаете, в каком сосуде больше жидкости? А будет ли одинаково давление, оказываемое на дно сосудов? С этими вопросами нам и предстоит разобраться. 

Вывод формулы

Выведем формулу для расчета давления жидкости на дно сосуда, имеющего форму прямоугольного параллелепипеда (рисунок 2).

Давление жидкости $p$ рассчитывается по формуле: $p = frac{F}{S}$, где $F$ — это сила, действующая на дно сосуда, а $S$ — это площадь дна сосуда.

1. Сила $F$ в данном случае равна весу $P$ жидкости, которая находится в сосуде;
2. Как узнать вес жидкости? Необходимо знать массу $m$ жидкости;
3. Массу $m$ мы можем вычислить по известной нам формуле: 
   $m = rho V$;

1. Так как нам известна жидкость, находящаяся в сосуде, мы знаем ее плотность . Остается вычислить объем $V$ жидкости. Обозначим высоту столба жидкости буквой $h$, площадь дна сосуда — $S$. Тогда объем можно вычислить по формуле:
   $V = Sh$;

1. Итак, подставляем наши данные в формулу для вычисления массы и получаем:
   $m = rho Sh$;

1. Таким образом, возвращаемся к весу жидкости и получаем, что: 
   $P = mg$, где $g$ — ускорение свободного падения, или $P = g rho Sh$.

С другой стороны, мы знаем, что вес столба жидкости равен силе, с которой жидкость давит на дно сосуда. Поэтому если мы разделим вес $P$ на площадь $S$, то получим искомое давление жидкости:
$p = frac{P}{S}$,
или $p =frac{g rho Sh}{S}$,

То есть:

$p = rho gh$.

Рассмотрим измерительные величины, которые мы будем использовать в данной формуле: плотность мы будем выражать в килограммах на кубический метр ($frac{кг}{м^3}$), $g = 9.8 frac{H}{кг}$, высоту столба жидкости  — в метрах ($м$). Тогда давление $p$ будет выражено в паскалях ($Па$).

Выводы

Так мы с вами вывели формулу для расчета давления жидкости на дно сосуда. Какие выводы мы можем сделать? 

От каких величин зависит давление жидкости на дно сосуда?

Давление жидкости не зависит от формы сосуда, оно зависит только от плотности жидкости и высоты ее столба.

Обратите внимание, что во многих случаях, когда говорят о высоте столба жидкости, говорят о глубине.

По какой формуле рассчитывают давление жидкости на стенки сосуда, давление внутри жидкости?

По формуле $p = rho gh$ можно вычислить давление на стенки сосуда или внутри жидкости, так как на одной глубине давление в жидкости будет одинаково во всех направлениях.

Вопросы и пример задачи

Посмотреть ответ

Скрыть

Посмотреть ответ

Скрыть ответ

Дано:
$rho = 800 frac{кг}{м^3}$
$h = 8 space м$

$p — ?$

Посмотреть решение и ответ

Скрыть

Упражнения

Дано:
$h = 0.6 space м$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

$p_1 — ?$
$p_2 — ?$
$p_3 — ?$

Показать решение и ответ

Скрыть

Дано:
$h = 10 space 900 space м$
$rho = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

$p — ?$

Показать решение и ответ

Скрыть

Дано:
$m = 5 space кг$
$h = 1 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

$S — ?$

Показать решение и ответ

Скрыть

Задания

Показать ответ

Скрыть

Дано:
$h = 0.086 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

$p — ?$

Показать решение и овет

Скрыть