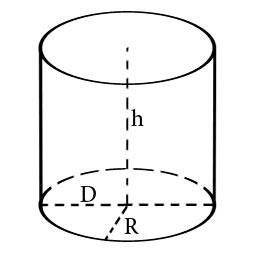
При помощи нашего калькулятора вы легко сможете узнать площадь цилиндра. Так же если вам необходимо узнать площадь бочки, круглой цистерны, круглого бака и т.д., то это калькулятор то, что Вам нужно.
|
|
|
| Вычислить площадь цилиндра через: | |
| Вычислить: | |
| Длина радиуса R: | |
| Высота цилиндра h: |
Для того что бы вычислить площадь цилиндра необходимо знать его высоту и радиус или диаметр. Если нам известны указанные величины, для нас не составит труда вычислить площадь.
Полная площадь цилиндра рассчитывается по следующим формулам:
- Если нам известен радиус:
S=2πR(h+R)
- Если нам известен диаметр:
S=πD(h+D/2)
Площадь боковой поверхности цилиндра рассчитывается по следующим формулам:
- Если нам известен радиус:
S=2πRh
- Если нам известен диаметр:
S=πDh
Где S – площадь, R – радиус, D – диаметр, h – высота, π – число Пи которое всегда примерно равно 3,14.
Как рассчитать площадь цилиндра
На данной странице калькулятор поможет рассчитать площадь поверхности цилиндра онлайн. Для расчета задайте высоту и радиус.
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Боковая поверхность
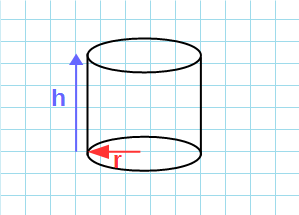
Формула площадь боковой поверхности цилиндра через высоту и радиус:
π – константа равная (3.14); r – радиус основания; h – высота цилиндра.
Полная поверхность

Формула площадь полной поверхности цилиндра через высоту и радиус:
π – константа равная (3.14); r – радиус основания; h – высота цилиндра.
Через диаметр цилиндра можно рассчитать его радиус и периметр основания цилиндра. Радиус будет равен половине диаметра, а периметр – его произведению на число π.
r=D/2
P=πD
Зная диаметр и высоту цилиндра, можно узнать площадь, объем, диагональ цилиндра и остальные параметры. Площадь боковой поверхности цилиндра представляет собой площадь прямоугольника, сторонами которого являются периметр основания цилиндра и его высота. Чтобы затем найти площадь полной поверхности цилиндра через диаметр и высоту, нужно к площади боковой поверхности добавить площадь верхнего и нижнего оснований, каждое из которых равно произведению числа π на четверть квадрата диаметра.
S_(б.п.)=hP=πDh
S_(п.п.)=S_(б.п.)+2S_(осн.)=πDh+(πD^2)/2=πD/2(2h+D)
P=πD
Объем цилиндра представляет собой площадь его основания, умноженную на высоту. Чтобы найти объем цилиндра через диаметр и высоту, нужно умножить квадрат диаметра на четверть числа π и на высоту.
V=(πD^2 h)/4
P=πD
Диагональ цилиндра находится из прямоугольного треугольника, в котором она является гипотенузой, а катеты представлены высотой и диаметром цилиндра. По теореме Пифагора диагональ цилиндра через высоту и диаметр цилиндра равна квадратному корню из суммы их квадратов. (рис. 25.1)
d=√(h^2+D^2 )
P=πD
Чтобы найти радиус сферы вписанной в цилиндр, если его диаметр равен высоте, нужно разделить диаметр цилиндра либо высоту на два, так как радиус вписанной сферы равен радиусу цилиндра. (рис.25.2)
r_1=h/2=D/2
P=πD
Радиус сферы, описанной вокруг цилиндра, при соблюдении тех же условий (равенство диаметра цилиндра и его высоты) равен половине диагонали цилиндра.(рис.25.3)
R=d/2=√(h^2+D^2 )/2
Площадь поверхности цилиндра
Рассчитайте онлайн площадь поверхности любого цилиндрического объекта.
Что известно
Размерность
Радиус основания
см
Диаметр основания
см
Высота
см
Раcсчитать
🧮 Что такое калькулятор площади цилиндра?
Калькулятор площади цилиндра — это онлайн-инструмент, который помогает рассчитать площадь поверхности цилиндра, исходя из его параметров.
Площадь поверхности цилиндра состоит из двух частей: площади боковой поверхности и площади оснований.
Для чего может быть использован такой калькулятор?
Калькулятор площади цилиндра может быть использован в различных областях, где требуется расчет площади поверхности цилиндрических объектов. Некоторые из возможных применений калькулятора площади цилиндра включают:
- Проектирование трубопроводов: при проектировании трубопроводов важно рассчитать не только объем жидкости или газа, но и площадь поверхности трубы, чтобы определить необходимое количество материала и затраты на изготовление трубопровода.
- Производство бочек и цистерн: при производстве бочек и цистерн необходимо рассчитать площадь поверхности, чтобы правильно распределить материалы и обеспечить надежность конструкции.
- Архитектура и строительство: при проектировании зданий, которые имеют цилиндрическую форму (например, башни, купола), необходимо рассчитать площадь поверхности, чтобы определить необходимое количество материалов для отделки или облицовки.
- Образование: калькулятор площади цилиндра может быть полезен для студентов и учителей при изучении геометрии и тела вращения.
В целом, калькулятор площади цилиндра может использоваться в любой сфере, где требуется подсчет площади цилиндрических объектов.
🛢️ Как и по какой формуле онлайн калькулятор рассчитывает площадь цилиндра?
Для расчета площади цилиндра онлайн калькулятор использует формулу:
S=2πR(h+R)
где:
- S – площадь цилиндра
- R – радиус основания цилиндра
- h – высота цилиндра
- π (Пи) – математическая константа, примерное значение которой равно 3.14159265359
Формула вычисляет площадь боковой поверхности цилиндра (2πrh) и площадь двух оснований цилиндра (2πr²), а затем складывает их для получения общей площади.
Онлайн калькулятор просто запрашивает у пользователя значения радиуса и высоты цилиндра, затем подставляет их в формулу и выводит результат площади цилиндра.
Широкое применение цилиндров в повседневной жизни
Цилиндр – это геометрическое тело, которое может использоваться в различных областях. Ниже приведены некоторые примеры использования цилиндра:
- Создание двигателей внутреннего сгорания: таких как двигатель автомобиля или мотоцикла.
- Механика: например в гидравлических цилиндрах, которые используются для перемещения или прессования тяжелых предметов.
- Создание емкостей: таких как баки для хранения газа или жидкости.
- Столярное дело: для создания столбов, колонн или других элементов архитектуры.
- Математика: для решения геометрических задач и для вычисления объемов и площадей тел.
- Кулинария: для формирования булочек, пирогов, кексов и других блюд.
- Сосуды для хранения и транспортировки жидкостей: таких как газы, масла, смазки и прочее.
- Научные исследования: например для измерения давления, температуры и других параметров.
❓Вопросы и ответы
Обратите внимание на ответы на некоторые часто задаваемые вопросы.
Какова формула для вычисления площади цилиндра?
Формула для вычисления площади цилиндра зависит от того, какую площадь вы хотите найти. Обычно вычисляют площадь боковой поверхности и площадь полной поверхности цилиндра. Для нахождения площади боковой поверхности цилиндра используйте формулу 2πrh, где r – радиус цилиндра, а h – его высота. Для нахождения площади полной поверхности цилиндра нужно прибавить к площади боковой поверхности удвоенную площадь оснований, т.е. используйте формулу 2πrh + 2πr^2.
Как использовать онлайн калькулятор для вычисления площади цилиндра?
Чтобы использовать онлайн калькулятор для вычисления площади цилиндра, вам нужно ввести значения радиуса и высоты цилиндра в соответствующие поля. Затем онлайн калькулятор автоматически рассчитает площадь цилиндра.
Как найти радиус цилиндра, если известна его площадь?
Для нахождения радиуса цилиндра по известной площади необходимо использовать формулу S = 2πrh + 2πr^2, где S – площадь цилиндра, r – радиус цилиндра, h – его высота. После подстановки известных значений в формулу можно найти радиус цилиндра.
Можно ли использовать онлайн калькулятор площади цилиндра для вычисления площади других геометрических фигур, таких как конус или сфера?
Нет, онлайн калькулятор площади цилиндра предназначен только для вычисления площади цилиндра. Для вычисления площади других геометрических фигур необходимо использовать соответствующие калькуляторы.
Каковы ограничения на значения радиуса и высоты, которые можно ввести в онлайн калькулятор площади цилиндра?
Онлайн калькулятор площади цилиндра не имеет ограничений на значения радиуса и высоты, которые можно ввести. Однако, для более точных результатов, рекомендуется использовать реалистичные значения.
Как мне использовать результаты вычислений, полученные с помощью онлайн калькулятора площади цилиндра?
Результаты вычислений, полученные с помощью онлайн калькулятора площади цилиндра, можно использовать для решения различных задач, связанных с геометрией, например, для расчета объема цилиндра, для определения необходимого количества материала для изготовления цилиндрического объекта или для определения количества жидкости, которая может поместиться в цилиндрический резервуар.
Поделитесь в соцсетях
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Площадь сечения сосуда
Сосуд — это емкость, предназначенная для ведения химических, тепловых и других технологических процессов, а также для хранения. Основными математическими характеристиками сосуда являются диаметр основания и высота.
Сечение сосуда — это изображение фигуры, образованной рассечением сосуда плоскостью в поперечном или продольном направлении.

Формула для расчета площади поперечного сечения сосуда:
S = π * d 2 / 4, где
d — диаметр сосуда.
Формула для расчета площади осевого сечения сосуда:
d — диаметр сосуда;
h — высота сосуда.
Формула для расчета площади параллельного оси сечения сосуда (бокового сечения сосуда):
a — хорда основания сосуда;
h — высота сосуда.
Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади поперечного или продольного сечения сосуда, если известны диаметр сосуда, длина хорды и высота сосуда. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения сосуда (площадь осевого сечения сосуда, площадь параллельного сечения сосуда, площадь бокового сечения сосуда и площади поперечного сосуда).
Источник
Площадь сечения сосуда с водой
Тема. Решение задач по теме «Гидростатика и гидродинамика».
Цели:
- — рассмотреть основные приемы решения расчетных задач на тему «Гидростатика и гидродинамика».
В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач.
Прежде чем приступить к выполнению задания, следует повторить основные законы гидромеханики.
Основной закон гидростатики — закон Паскаля, согласно которому в состоянии равновесия давление жидкости в данной точке не зависит от ориентации площадки, на которую она действует.
Поскольку в школьном курсе рассматривается стационарное течение несжимаемой жидкости, то будет справедливо уравнение неразрывности струи.
Для идеальной жидкости выполняется уравнение Бернулли. Покажите, что уравнение Бернулли является следствием закона сохранения энергии.
- К концам равноплечного рычага подвесили две одинаковые гири. Что произойдет, если одну гирю поместить в воду, а другую в керосин?
Ответ: равновесие нарушится.
Почему, если близко стоишь около быстро идущего поезда, возникает эффект «притягивания» к колесам?
Ответ: проходящий поезд увлекает за собой примыкающие к нему слои воздуха. Воздух, движущийся между человеком и поездом, оказывает на него меньшее давление, чем неподвижный. Эта разность давлений и обусловливает силу, увлекающую человека к поезду.
 Проделайте эксперимент. Вложите в воронку бумажный фильтр (рис. 1) и попробуйте выдуть его через узкий конец воронки. У вас не получилось? Почему?
Проделайте эксперимент. Вложите в воронку бумажный фильтр (рис. 1) и попробуйте выдуть его через узкий конец воронки. У вас не получилось? Почему?
Ответ: чем сильнее вы вдуваете воздух, тем плотнее фильтр входит в воронку. Объясняется это с помощью закона Бернулли, согласно которому давление понижается в местах сужения. В узком просвете между воронкой и бумажным фильтром давление понижается, и внешнее атмосферное давление удерживает фильтр в воронке.
Примеры решения расчетных задач
Задача 1. Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда S1, сечение струи S2 (рис. 2). Найдите ускорение, с которым перемещается уровень воды в сосуде.
Будем считать жидкость несжимаемой. Тогда для каждого момента времени, согласно уравнению неразрывности струи, можно записать
S1v1 = S2v2, (1)
где v1 — скорость воды в сосуде, v2 — скорость воды в струе вблизи отверстия.
Возьмем производную по времени от (1)

где 


Ответ: 
Задача 2. 
Согласно закону Паскаля давление на жидкость передается во всех направлениях одинаково, поэтому в первом случае давление, производимое на пластинку жидкостью, равно гидростатическому давлению столба жидкости высотой h, а значит, F1 = ρghS , где ρ — плотность жидкости.
Во втором случае сила F2 согласно второму закону Ньютона равна изменению импульса жидкости в единицу времени

Изменение импульса Δp = Δmv , где Δm — масса жидкости, вытекающей в единицу времени, v — скорость истечения жидкости из отверстия.
Масса вытекающей жидкости Δm = ρgS, скорость истечения согласно формуле Торричелли 
Таким образом, F2 = 2F1 . Объяснить это можно так. Когда жидкость вытекает из малого отверстия, линии тока вблизи него сгущаются, а значит, как следует из уравнения Бернулли, давление на стенку вблизи отверстия уменьшается. Поэтому сила реакции вытекающей струи оказывается больше силы статического давления на площадь отверстия.
Задача 3. 
Решение: Воспользуемся условием стационарности течения несжимаемой жидкости

Для идеальной жидкости справедливо уравнение Бернулли:

Поскольку жидкость свободно падает, то давления в обоих сечениях одинаковы, и уравнение Бернулли принимает вид:

За время t через любое сечение протекает один и тот же объем воды, поэтому можно записать

Выразим скорость v1 из (1) и (2):

Подставим полученное значение v1 в (3) и получим окончательный ответ:

Ответ: 
Задача 4. 
Так как из шприца вытечет вся находившаяся в нем жидкость, то
S1l = S2v2t, (5)
где v2 — скорость истечения струи. Будем считать жидкость идеальной, тогда можно использовать уравнение Бернулли:

Шприц расположен горизонтально, следовательно, h = const. Уравнение Бернулли тогда запишется следующим образом:

где Ра — атмосферное давление, а v1 — скорость движения поршня. Из уравнения неразрывности следует

отсюда

Подставляя найденное значение v2 в (5), получим

Так как S2 << S1 , то можно записать

Задачи для самостоятельной работы
- «Вечерело. Уставший за нелегкий трудовой день Абдулла Ибн Сауд присел на берегу реки и стал обдумывать свой социальный статус. В колхоз не берут, кооперативы эмир разогнал, к нему самому на службу устраиваться — так стражники без золотых во дворец не пускают. Эх, жизнь… Но тут взгляд Абдуллы остановился: по реке плыл какой-то предмет, и лишь маленький кусочек сургуча был виден над водой. Абдулла бросился в воду и вытащил оттуда старинный глиняный кувшин, герметично закупоренный сургучом. Распечатав кувшин и перевернув его, Абдулла обомлел: сверкнуло золото. Из кувшина высыпалось 147 одинаковых золотых монет. Монеты Абдулла спрятал, а сосуд запечатал и бросил обратно в воду. Поплыл сосуд дальше, примерно треть его объема торчало над водой». Так говорится в одной из восточных сказок. Предполагая, что кувшин был двухлитровый, оцените массу одной золотой монеты.
Ответ: m = 4,45 г.
На некоторых железных дорогах пополнение паровозного котла водой производится без остановки паровоза. Для этой цели применяется изогнутая под прямым углом труба, которая опускается на ходу паровоза в канаву с водой, проложенную вдоль рельсов. При какой скорости паровоза вода может подняться на высоту 3 м?
Ответ: v = 28 км/ч.
Из поднятого на высоту h резервуара выходит труба постоянного сечения S, переходящая в короткую трубу сечением S1, перекрытую краном. Найдите давление в магистральной трубе при открытом кране.
Ответ: Р = Ратм + ρgh
Определите расход воды Q, протекающей через слив плотины, имеющей ширину l, глубину потока d и понижение уровня потока по сравнению с уровнем воды в водохранилище, равное h.
Ответ: Q = ρdl·√(2gh).
Какова примерно скорость катера, если при его движении вода поднимается вдоль его носовой части на высоту h = 1 м?
Ответ: v ≈ √(2gh) ≈ 4,4 м/с.
На гладкой горизонтальной поверхности стоит цилиндрический сосуд с водой. В боковой стене сосуда у дна имеется отверстие площадью S0. Какую силу нужно приложить к сосуду в горизонтальном направлении, чтобы удержать его в равновесии? Площадь поперечного сечения сосуда равна S, высота столба жидкости h.
Ответ: 
На поршень шприца площади S действует сила F. С какой скоростью v должна вытекать в горизонтальном направлении струя из отверстия иглы площади s? Плотность жидкости ρ. Трением пренебречь.
Ответ: 

Источник