что такое площадь цилиндрического сосуда и как зная её и обьём с плотностью жидкости найти высоту сосуда
Знаток
(365),
закрыт
10 лет назад
rafael ahmetov
Высший разум
(122431)
10 лет назад
Нет такого понятия площадь сосуда или площадь цилиндра. Для цилиндра существуют понятия площадь основания S(осн.) =Пи*R^2, площадь боковой поверхности S(бок.) =2*Пи*R*H, площадь полной поверхности S(п.) =Пи*R*(R+2*H), и объем V=Пи*R^2*H.
Чтобы найти неизвестную высоту цилиндра по известному объему и одной из вышеперечисленных площадей, нужно решить систему из двух уравнений (объема и соответствующей площади).
Как определить площадь дна сосуда Если известна масса сосуда объем жидкости и ее давление на площадь стола
Найди верный ответ на вопрос ✅ «Как определить площадь дна сосуда Если известна масса сосуда объем жидкости и ее давление на площадь стола …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Физика » Как определить площадь дна сосуда Если известна масса сосуда объем жидкости и ее давление на площадь стола
Сообщающиеся сосуды, теория и онлайн калькуляторы
Сообщающиеся сосуды
Определение сообщающихся сосудов
Определение
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=]
[=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Содержание:
Определение площади и объема:
В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски.
Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.
|
Рис. 6.1. |
Рис. 6.2. |
Рис. 6.3 |
Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле:
S = a · b, (6.1)
где a – ширина прямоугольника, b – высота.
Площадь параллелограмма ABCD (рис. 6.2) также находится по формуле 6.1. Площадь квадрата найти легко, поскольку его ширина и высота одинаковы:
S = a · a = a2 , (6.2)
Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле:
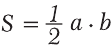
Проблема определения площади круга была решена еще в Древней Греции. Для этого нужно знать радиус круга и число «пи», приблизительное значение
которого π ≈ 3,14.
Площадь круга равняется
S = π · R2, (6.4) .
Значение числа 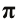
Вычисление объема простых фигур
Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):
|
Рис. 6.4. |
Рис. 6.5. |
|
V = a · b · h (6.4)
Поскольку S = a · b,
где S – это площадь основания ящика, то формулу (6.4) можно переписать и так:
V = S · h (6.5)
У куба все ребра равны, потому его объем равняется:
V = a · a · a = a3 (6.6)
Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть:
V = S · h = πR2 · h (6.7)
Объем шара (рис. 6.6)
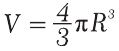
Единицы измерения объема
Поскольку длину сторон измеряют в единицах длины (метр, дециметр, сантиметр и т. д.), то единицы измерения объема – это единицы длины, возведенные в третью степень.
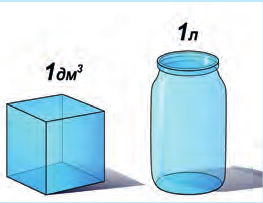
Куб с ребром 1 м имеет объем 1 м3 (один кубический метр). Один литр (1 л) по определению – это объем куба с ребром 1 дм (рис. 6.7), то есть 1 л = 1 дм3 (дециметр кубический). Один литр равен 1000 кубических сантиметров: 1 л = 1000 см3. Объем в один сантиметр кубический еще называют миллилитром, то есть тысячной частью литра (1 мл = 0,001 л).
Рис. 6.7. Один литр – это 1дм3
Напомним, что дециметр – это десятая часть метра, а сантиметр – сотая часть метра
Таблица 6.1
| 1 м3 = 1 000 л | 1 м3 = 1 000 000 см3 |
| 1 л = 1 дм3 | 1 л = 1000 см3 |
| 1 дм3 = 1 000 см3 | 1 л = 1 000 мл |
| 1 см3 = 1 мл | 1 мл = 0,001 л |
- Заказать решение задач по физике
Измерение объема тел неправильной формы
Прибор для измерения объема называют мензуркой, или мерным цилиндром (рис. 6.8). Мензурка – это прозрачный сосуд с нанесенными делениями, которые обозначают объем в миллилитрах. Дома у вас наверняка есть мерный стакан, то есть та же мензурка. Литровой или поллитровой банкой, или стаканом (250 мл) также можно пользоваться, если не нужна большая точность. С помощью мензурки можно определить объем жидкости и тела неправильной формы. Для этого в мензурку нужно налить воду и определить объем этой воды. Потом полностью погрузить тело в воду и запомнить новое значение объема. Разница измеренных значений равна объему тела.
Рис. 6.8. Деления мензурки определяют объем в миллилитрах (то есть в см3)
История:
 |
Существует легенда, согласно которой первым такой способ определения объема изобрел древнегреческий ученый Архимед. Произошло это во время размышлений над довольно сложной зада-чей, предложенной царем Гиероном. Идея решения возникла тогда, когда Архимед влез в ванну и заметил, что уровень воды поднялся. Ученый понял, что вытесненный объем воды как раз равен объему погруженного в нее тела. Восторженный Архимед выпрыгнул из ванны и выбежал на улицу с криком «Эврика! Эврика!», что в переводе с древнегреческого значит «На-шел! Нашел!». |
Итоги:
- Площадь тел правильной формы равна произведению основы на высоту и измеряется в квадратных единицах длины S = a · b.
- Объем тел правильной формы определяется как произведение площади основы на высоту и измеряется в кубических единицах V = S · h.
- Объем тел произвольной формы определяют с помощью мензурки
- Площадь круга определяют по формуле S = π · R2.
- Объем шара равен
.
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Что изучает механика в физике
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
- Точность измерений и погрешности
Конспект по физике для 7 класса «Расчёт давления жидкости на дно и стенки сосуда». ВЫ УЗНАЕТЕ: Что такое гидростатическое давление. Как рассчитать давление жидкости на дно сосуда. Как рассчитать давление жидкости на стенки сосуда. ВСПОМНИТЕ: Как формулируется закон Паскаля? Как определить давление твёрдого тела на опору? Как зависит масса тела от его плотности? Что такое вес тела? Как вес тела зависит от его массы?
Конспекты по физике Учебник физики Тесты по физике
Расчёт давления жидкости на дно и стенки сосуда
Жидкость, находящаяся в сосуде, оказывает давление как на дно сосуда, так и на его стенки. Поверхность жидкости, которая не соприкасается со стенками сосуда, называют свободной поверхностью жидкости. Давление, оказываемое покоящейся жидкостью, называют гидростатическим.
РАСЧЁТ ДАВЛЕНИЯ ЖИДКОСТИ НА ДНО СОСУДА
Вычислим давление жидкости на дно сосуда площадью S, если высота столба жидкости в этом сосуде равна h. Как известно, давление определяется по формуле p = F/S.
В нашем случае сила F, с которой жидкость действует на дно сосуда, равна её весу. Вес жидкости определяется по формуле Р = mg. (1)
Следовательно, для определения веса жидкости необходимо найти её массу. Для этого воспользуемся формулой m = pV, где р — плотность жидкости, а V — объём жидкости. Для определения объёма необходимо найти произведение площади дна сосуда и высоты столба жидкости: V = Sh.
Следовательно, масса жидкости в сосуде определяется по формуле m = рSh. (2)
Подставим это выражение в формулу (1) и получим Р = gpSh. (3)
Теперь для нахождения давления необходимо вес жидкости разделить на площадь сосуда: P = gpSh/S
Сократив в полученном выражении S в числителе и знаменателе, получим формулу для расчёта давления жидкости на дно сосуда: p = pgh. (4)
Давление жидкости на дно сосуда рассчитывают по формуле p = pgh.
РАСЧЁТ ДАВЛЕНИЯ ЖИДКОСТИ НА СТЕНКИ СОСУДА
Так как по закону Паскаля давление внутри жидкости на одном и том же уровне одинаково по всем направлениям, то по формуле (4) можно находить давление жидкости на стенки сосуда на любой глубине.
Из формулы (4) видно, что давление жидкости на дно и стенки сосуда прямо пропорционально высоте столба жидкости и зависит по только от высоты столба жидкости, но и от плотности жидкости р. Чем больше плотность жидкости, тем большее давление она оказывает при условии, что высота столба жидкости остаётся постоянной.
Даже при использовании дыхательных трубок, выступающих над водой, глубина погружения человека не может превышать 1,5 м, так как из-за давления воды у него не хватает сил увеличив объём грудной клетки и вдохнуть воздух. В 1943 г французами Ж. Кусто и Э. Ганьяном был изобретён акваланг специальный аппарат со сжатым воздухом, предназначенный для дыхания под водой и позволяющий находиться под водой от нескольких минут (на глубине около 40 м) до часа и более.
В соответствии с формулой (4) давление жидкости также зависит от ускорения свободного падения g. Значит, если представить себе один и тот же сосуд с жидкостью, помещенный на разные планеты, то давление на дно и стенки сосуда в нем будет различно в зависимости от значения g на планете.
ГИДРОСТАТИЧЕСКИЙ ПАРАДОКС
Из формулы (4) видно, что давление жидкости на дно и стенки сосуда зависит только от плотности и высоты столба жидкости и не зависит от формы сосуда.
Приведённая схема опыта показывает, что сила, с которой жидкость оказывает давление на дно сосудов различной формы, но с одинаковой площадью дна и одинаковой высотой столба жидкости в них, будет одной и той же. Каждый из сосудов снабжён съемным дном, и динамометры показывают именно 3 силу воздействия воды на дно сосудов, но не вес жидкости. Очевидно, что вес жидкости в сосудах будет различным, так как объёмы жидкости в сосудах неодинаковы.
По закону Паскаля давление столба жидкости высотой h равномерно передаётся в любую точку дна каждого из сосудов. Именно поэтому сила, с которой жидкость оказывает давление на дно, больше веса жидкости в сосуде В, но меньше веса жидкости в сосуде С. Несмотря на кажущееся противоречие, ничего парадоксального в этих опытах нет.
ОПЫТ ПАСКАЛЯ
Даже небольшим количеством воды можно создать очень большое давление. В 1648 г. этот факт очень убедительно продемонстрировал В. Паскаль, поразив своих современников. В прочную, наполненную водой и закрытую со всех сторон бочку площадью поверхности 2 м2 была вставлена тоненькая трубочка площадью сечения 1 см2 и высотой 5 м. Затем Паскаль поднялся на балкон второго этажа и влил в эту трубочку всего кружку воды. Из-за малого диаметра трубки вода поднялась до большой высоты, и давление на стенки бочки так возросло, что планки (клёпки) бочки разошлись и вода стала вытекать из бочки.
Вы смотрели Конспект по физике для 7 класса «Расчёт давления жидкости на дно и стенки сосуда»: Что такое гидростатическое давление. Как рассчитать давление жидкости на дно сосуда. Как рассчитать давление жидкости на стенки сосуда.
Вернуться к Списку конспектов по физике (В оглавление).
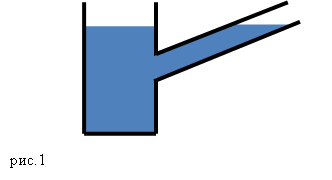
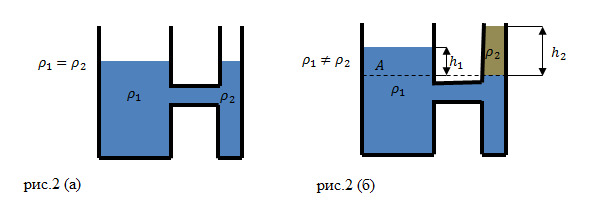
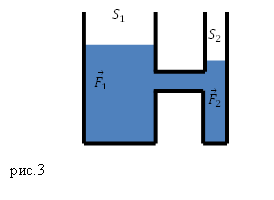
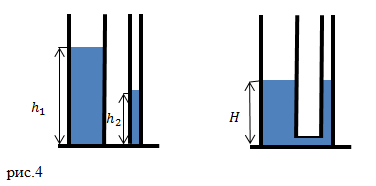
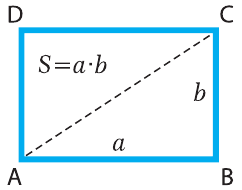
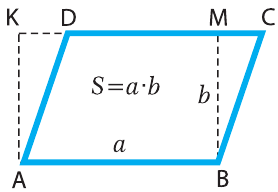
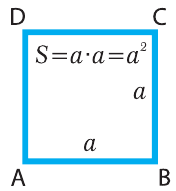
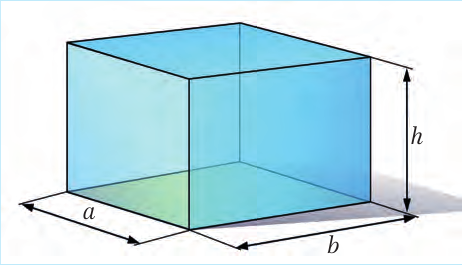
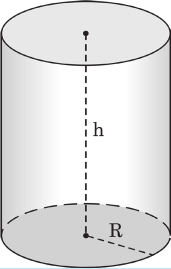
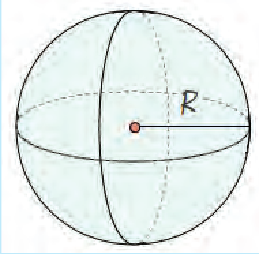 Рис. 6.6.
Рис. 6.6.